计及风光出力相关性的静态电压稳定概率分析

卢锦玲，何振民，魏方园，贾静然

(华北电力大学 电气与电子工程学院，河北 保定 071003)



计及风光出力相关性的静态电压稳定概率分析

卢锦玲，何振民，魏方园，贾静然

(华北电力大学 电气与电子工程学院，河北 保定 071003)

摘要：基于Copula函数和非参数核密度估计，建立计及风光出力相关性的离散联合概率分布，针对不同状态进行连续潮流计算，得到节点电压、系统负荷裕度和临界电压的离散概率分布，采用半不变量和Gram-Charlier级数拟合负荷裕度和临界电压的分布曲线。以风电场和光伏电站接入IEEE14系统为例对本文方法进行验证，与蒙特卡洛模拟法和随机响应面法进行比较，结果证明所提方法的正确性和精度，并对风光不同相关性进行仿真分析。最后以节点电压方差、临界电压和负荷裕度均值为指标对系统电压稳定进行分析，对系统薄弱节点进行无功补偿以提高电压稳定性。

关键词：电压稳定；风电场；光伏电站；相关性；无功补偿

0引言

近年来，全球能源安全和环境恶化等问题，使得充分利用可再生能源已经成为全球共识，风电和光伏发电以其可再生、无污染等优点得到大力发展。风电和光伏发电受天气影响很大，出力随机性、波动性较强，大规模风电场/光伏电站接入电网对系统电压稳定产生不利影响[1-2]。

目前，含风电场/光伏电站电力系统电压稳定分析大都采用确定性分析方法，不能体现风光出力随机性对系统电压稳定的影响。概率潮流可以深刻全面反映随机因素对系统状态变量的影响，主要有蒙特卡洛(Monte Carlo, MC)模拟法[3-5]和解析法[6-8]，但是概率潮流只能得到系统节点电压和支路功率的概率分布参数并不能全面反映系统电压稳定。系统负荷裕度和临界电压是衡量电压稳定的重要指标，掌握其概率分布信息有利于全面进行电压稳定分析，文献[9]基于随机响应面法(stochastic response surface method，SRSM)和连续潮流法，建立含风电场电力系统静态电压概率评估模型，通过连续潮流计算得到负荷裕度的概率分布信息。文献[10-11]基于点估计法和柯尼-费歇尔(Cornish-Fisher)级数对含分布式电源的配电网进行电压稳定概率评估，但同一地区分布式电源出力具有相关性，忽略相关性将对评估结果产生不利影响。文献[12]基于正交变换技术处理风电场之间出力相关性，采用随机响应面法和非线性规划模型求解负荷裕度的概率分布参数。以上文献均假定风速服从威布尔(Weibull)分布，光照强度服从贝塔(Beta)分布，通过风速功率曲线、光照强度和光伏电站出力关系式得到风电场和光伏电站出力值，风光出力不仅取决于风速和光照强度，还与控制策略、风机布局、光伏电池倾角等因素有关。在此假定条件下，风光出力不免会有一定误差[13]。

本文采用非参数核密度估计和Copula函数建立风光出力联合概率密度函数，通过出力离散化和双重积分得到离散联合概率分布，结合连续潮流计算，得出系统节点电压、负荷裕度和临界电压的离散概率分布，采用半不变量和Gram-Charlier级数拟合负荷裕度和临界电压的分布曲线。IEEE14节点系统计算结果验证所提方法的正确性和计算精度，并对不同风光相关性对负荷裕度的影响进行了分析比较，最后以节点电压方差、越限概率、负荷裕度和临界电压均值为指标，对风电场和光伏电站接入IEEE14节点系统电压稳定进行分析，并对系统薄弱节点进行无功补偿，以提高电压稳定性。

1风光出力联合概率密度模型

本文根据某地风电场和光伏电站出力历史数据，采用非参数核密度估计方法估计风光出力的概率分布，基于Copula理论建立计及风光出力相关性的联合概率密度模型。

1.1核密度估计

核密度估计(Kernel Density Estimation, KDE)是从样本数据估计分布特征的非参数估计方法[14]。假设x1、x2、…、xn为随机变量X的n个样本点，令X的概率密度函数为f(x)，则f(x)的核密度估计为式(1)[15]：

(1)

式中：n为样本容量；h为带宽；K(·)为核函数。核函数选取以0为中心的对称单峰概率密度函数，本文采用文献[14]的高斯核函数对风电场和光伏电站出力值进行估计。

取风电场和光伏电站出力标幺值为随机变量Pw和Ppv，(Pw1，Pw2，…，Pwn)和(Ppv1，Ppv2，…，Ppvn)分别为Pw和Ppv的样本空间，将其分别带入式(1)可得Pw和Ppv的概率密度估计f(Pw)和f(Ppv)，通过积分运算得到累计概率分布曲线F(Pw)和F(Ppv)。

1.2Copula函数

文献[16]给出Copula函数的严格定义，即Copula函数是将N维联合分布函数F(x1、x2、…、xn)与各随机变量边缘分布函数F(x1)、F(x2)、…、F(xn)相连接的函数。即存在函数C(u1，u2，…，un)使得式(2)成立[17]。

(2)

联合概率密度函数如式(3)所示，由Copula函数的导函数c(u1，u2，…，un)和边缘分布函数F(x1)、F(x2)、…、F(xn)的密度函数求出。

(3)

其中c(u1，u2，…，un)=∂C(u1，u2，…，un)/ ∂u1…∂u2，f(x1)，…，f(xn)分别为边缘分布函数F(x1)、F(x2)、…、F(xn)的密度函数。

同一地区，风电场和光伏电站出力具有相关性，在Copula函数族中，Gumbel Copula和Clayton Copula函数只能描述变量间的非负相关关系，Frank Copula函数既可以描述非负相关关系也可以描述负相关关系[13]，此外，Frank Copula函数为对称分布，没有明显的后尾特性，分布比较均匀，故选取Frank Copula函数作为二者出力联合概率分布的连接函数。线性相关系数ρ只能表示服从正态或线性分布的随机变量之间的相关性，而Kendall秩相关系数τ能在一定程度上克服非正态性的弱点，选取Kendall秩相关系数τ度量风电场和光伏电站出力相关性。τ与θ的关系如式(4)所示，风光出力联合概率密度函数如式(5)所示：

(4)

(5)

式中：u=F(Pw)；v=F(Ppv)；Pw和Ppv分别为风电场和光伏电站出力标幺值；θ为Copula函数相关参数[13]。

2离散化的联合概率分布

概率潮流计算以线性化潮流模型为基础[17]，当风电场和光伏电站出力波动较大时，导致系统状态变量的变化未必符合线性化潮流方程，本文对风电场和光伏电站出力离散化，并对1.2节联合概率密度函数进行积分运算得到风光出力的离散联合概率分布。由Copula函数得到的联合概率密度函数定义域为[0,1]×[0,1]，在风电场和光伏电站出力变化范围内均匀选取离散点，离散策略如图1所示。

在风电场出力变化范围内均匀分成m个区间，即步长a=1/m，当风电场出力界于[i/m,(i+1)/m]之间时，其功率值Pwi近似为[i/m+(i+1)/m]/2。光伏电站出力离散化策略与风电场相同，在光伏出力范围内均匀分成n个区间，步长b=1/n，当光伏电站出力在[j/n,(j+1)/n]时，

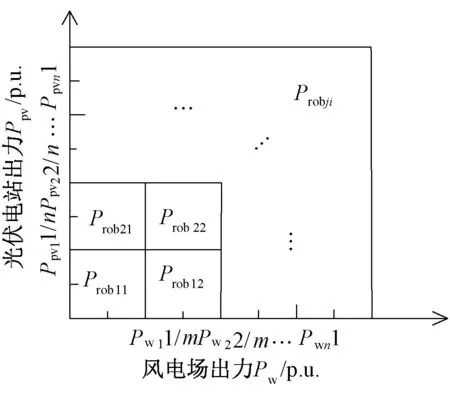
图1　风光出力离散化策略Fig.1　Discretization strategy of power output of wind farm and PV plant

功率值Ppvj近似为[j/n+(j+1)/n]/2，当风电场和光伏电站出力分别为Pwi和Ppvj时，对应的概率如式(6)所示。

(6)

风电场中双馈风力发电机组采用恒功率因数控制方式时，风电场节点可做PQ节点处理，当风电场有功出力为Pwi时，无功出力Qwi为式(7)：

(7)

式中：Pwi和Qwi为风电场有功和无功出力；cosφ为功率因数。

在稳态运行时，光伏逆变器有恒功率因数控制和恒电压控制方式[18]，本文在进行潮流计算时，光伏电站并网点作为PQ节点，当有功出力为Ppvi时，无功出力Qpvi为式(8)：

(8)

式中：Ppvi和Qpvi为光伏电站有功无功出力；cosθ为光伏电站功率因数，表1为风光出力离散化联合概率分布模型。

表1风光出力离散化联合概率模型

Tab.1Joint discrete probabilistic model of power output of wind farm and PV plant

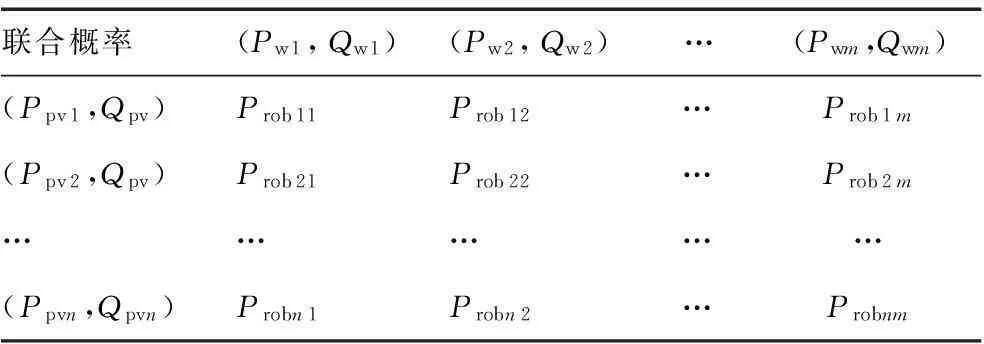
联合概率(Pw1,Qw1)(Pw2,Qw2)…(Pwm,Qwm)(Ppv1,Qpv)Prob11Prob12…Prob1m(Ppv2,Qpv)Prob21Prob22…Prob2m……………(Ppvn,Qpvn)Probn1Probn2…Probnm

3基于离散概率模型的电压稳定性分析

连续潮流(Continuation Power Flow, CPF)引入负荷参数λ，解决了在临界点附近潮流不收敛的问题。从系统稳定工作点开始，负荷按照一定方向变化，沿PV曲线对系统下一工作点进行预估、校正，直至勾画出完整的PV曲线，得到系统负荷裕度和临界电压，物理意义明显且有较高的线性度，在静态电压稳定分析领域得到广泛应用。

在离散概率模型的基础上，对每一风光出力组合状态进行连续潮流(CPF)计算，理论上需进行m×n次计算，由于风光出力具有相关性，联合概率大于0的次数小于m×n。通过连续潮流计算得到系统负荷裕度、临界电压和各节点电压的离散概率分布，如表2所示。

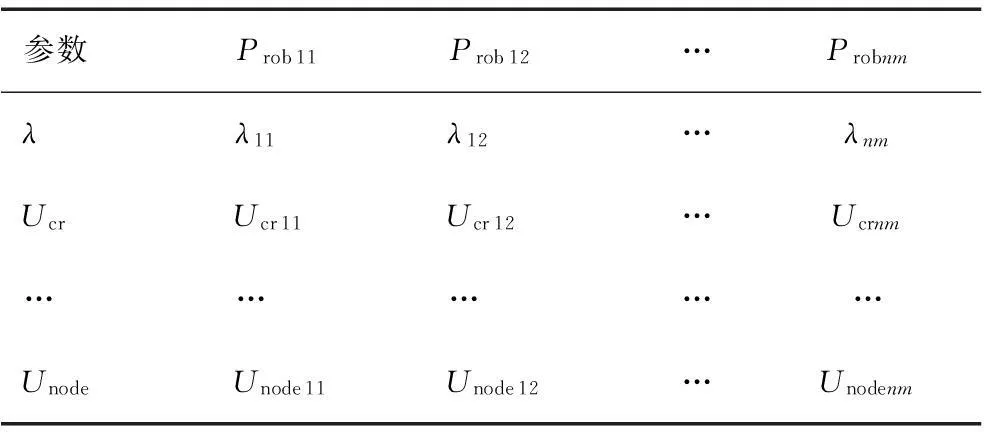
表2　系统状态变量的离散概率分布

基于上述离散概率分布，可得到系统负荷裕度、临界电压和各节点电压的各阶原点矩和中心矩如式(9)和式(10)：

(9)

(10)

式中：αm(x)，Mm(x)分别为系统状态变量的m阶原点矩和中心矩(m=1,2…)，Probji为对应状态变量取值的概率。

各阶半不变量Ki与中心矩Mm的关系为

(11)

已知各阶半不变量，利用Gram-Charlier级数拟合随机变量的累计概率分布函数[19]，本文采用8阶Gram-Charlier级数展开逼近累计概率分布函数。

拟合的分布函数表达式为式(12)：

(13)

式中：z为标准化后的随机变量；gi为规格化的各阶半不变量；Φ(z)和Ψ(z) 分别为标准正态分布随机变量的累计分布函数和概率密度函数；Hi(z)为i阶Hermite多项式。

对于式(9)和式(10)，当m=1时，α1(x)，M1(x)分别为状态变量的期望值和方差，期望值反映状态变量的平均值，方差反映状态变量波动大小，本文以节点电压方差、节点电压越限概率、节点临界电压和负荷裕度为指标对系统电压稳定进行分析，并对系统薄弱节点进行无功补偿以提高电压稳定性。

4算例

4.1系统概况

风电场和光伏电站通过变压器分别接入IEEE14节点标准测试系统的14号节点和9号节点，在该系统中，有一个平衡节点(节点1)，4个PV节点(节点2、3、6、8)，其余为PQ节点，系统中总有功负荷295 MW，无功负荷73.5 MVar，风电场和光伏电站额定容量均为20 MW，采用恒功率因数方式运行，功率因数为0.95(滞后)。在matlab R2014a平台借助matpower实现本文电压稳定概率分析方法。

4.2方法验证

在不考虑其它随机因素的情况下，以节点10增加负荷为例进行连续潮流计算。为验证本文方法的正确性，采用3种方法进行分析，方法(1)1 000次蒙特卡洛模拟。方法(2)基于正交变换技术和随机响应面法[12]进行分析。方法(3)采用本文方法分别对离散步长a=b=1/10，a=b=1/15和a=b=1/20 三种情况进行计算。节点9、14节点电压、负荷裕度和临界电压的累计概率分布曲线如图2所示。

从图2可以看出，(1)当离散步长为a=b=1/20时，3种方法计算得到的累概率分布曲线基本吻合，从而验证了本文方法的正确性。(2)当离散步长a=b=1/10时，累计概率分布与其它两种方法有一定误差，当离散步长小于1/15时，误差已经明显减小。

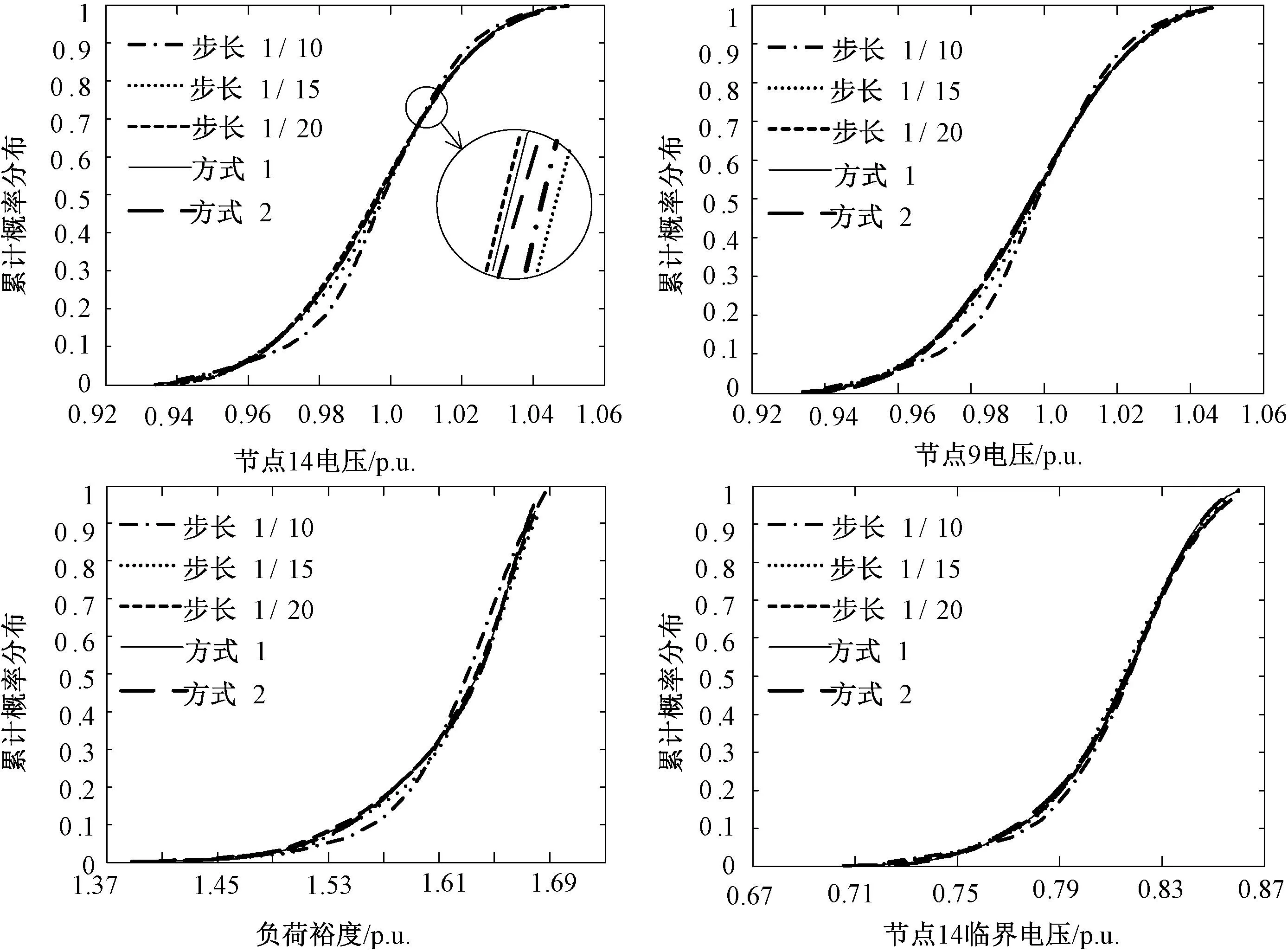
图2　累计分布函数Fig.2　Cumulative distribution functions

当步长取a=b=1/15时，以上3种方法得到的节点电压、临界电压和负荷裕度期望值和方差的比较如表3所示，Un为节点电压，Ucr为节点临界电压，λ为节点负荷裕度。从表3可以得出，与方法1相比，方法3计算负荷裕度的相对误差在0.6%以内，比方法2的误差小，验证了计算结果的精度。以节点14电压均值为例，以方法1计算结果为参考，其相对误差随步长变化的曲线如图3所示。从图3可以看出，随着离散化步长的增大，节点电压均值误差逐渐增大。当步长小于1/15时，节点电压均值误差能控制在0.05%以内，当步长大于1/15时，均值相对误差增大，但也在允许范围内。通过步长控制可以控制计算精度，若系统对计算速度要求较高时，可以适当增大离散步长，反之则减小离散步长。

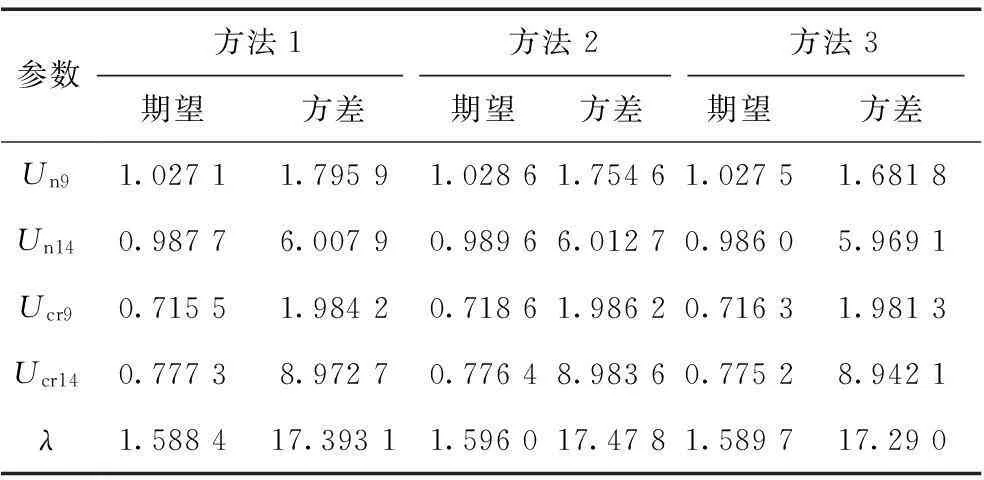
表3　期望和方差比较

注：方差数量级为(10-4)

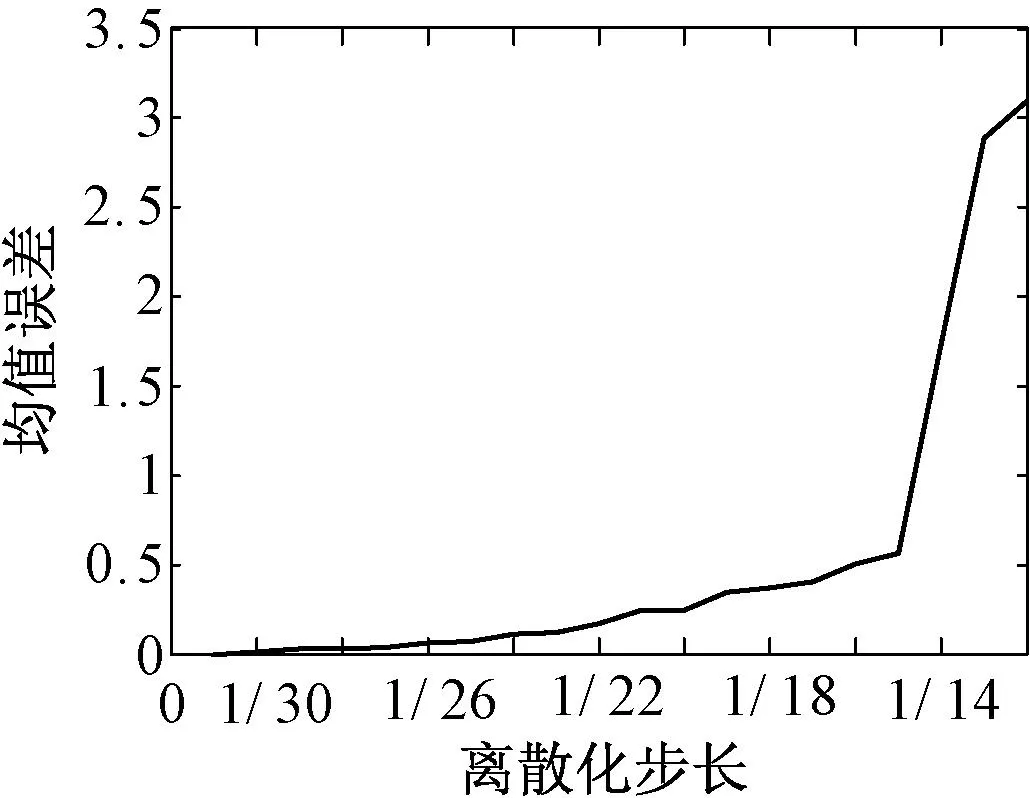
图3　误差随步长变化Fig.3　Errors with step change

4.3风光出力相关性对负荷裕度的影响

研究风光出力不同相关性对系统负荷裕度的影响，以上述系统为研究对象，以秩相关系数τ描述相关性，分别对风光出力存在正相关、负相关和无相关性的情况进行分析。负荷裕度的累计概率分布如图4所示。

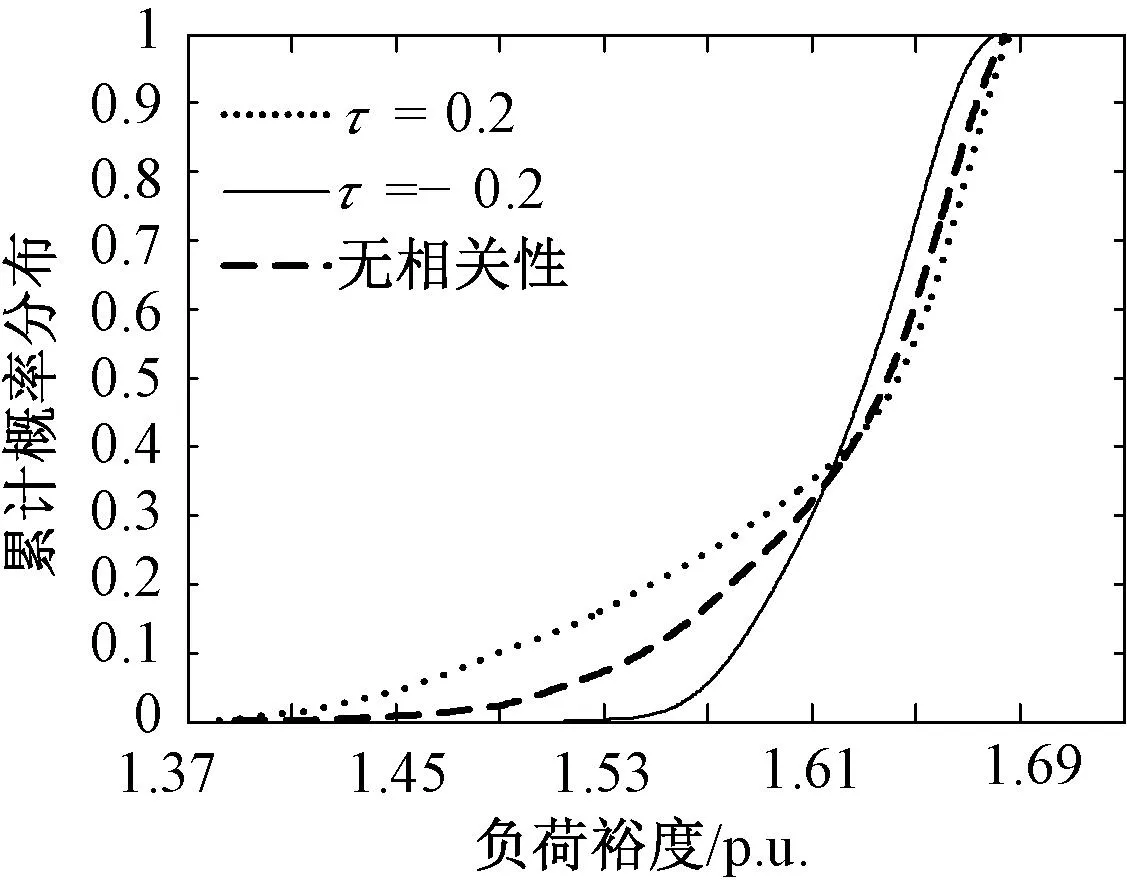
图4　负荷裕度累计概率分布曲线Fig.4　Cumulative distribution curve of load margin

从图4可以看出，当风光出力存在负相关性时，负荷裕度波动范围小，约为0.12 p.u.，负荷裕度最小值为1.55 p.u.，此时，风电场和光伏电站出力可以互补，电压稳定性较好；当风光出力存在正相关性时，负荷裕度波动范围大，约为0.28 p.u.，负荷裕度最小值为1.39 p.u.，此时，则不利于电压稳定。在含风电场和光伏电站的电力系统中，忽略出力相关性将对计算结果产生较大误差，使计算结果过于保守或过于乐观。

4.4风光接入对电压稳定的影响

以风电场和光伏电站实测出力为数据来源，以上述系统为算例进行电压稳定分析，系统PQ节点电压和临界电压的均值以及各节点电压越限情况如表4所示。

从表4可以看出，风电场和光伏电站接入系统后，除离平衡节点较近的节点4和5以外，其它节点临界电压和电压均值均减小，电压稳定性降低。节点9、10、11和14临界电压均值较低，为系统薄弱节点。从节点电压方差可以看出，风电场和光伏电站接入后，系统各节点电压波动增大，节点14、9和10由于远离PV节点，临近风电场和光伏电站接入点，电压波动最大，且节点14有越限风险。风光接入前，节点10负荷裕度均值为1.695，接入后该节点负荷裕度均值为1.589，负荷裕度减小，再次验证风光接入后系统电压稳定性降低。

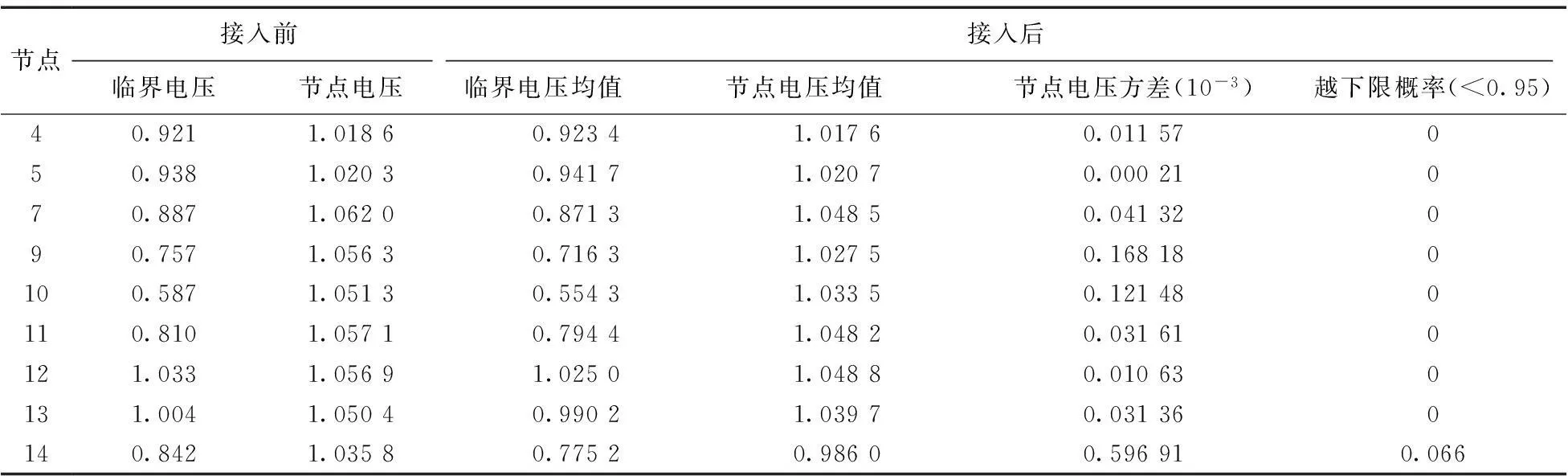
表4　节点电压期望和方差

综上分析，选择节点9、10和14为无功补偿点，在该节点安装5Mvar并联电容器进行无功补偿，补偿后节点电压均值、方差和节点负荷裕度如表5所示。

从表5可以看出，无功补偿后节点电压、临界电压和节点负荷裕度的方差均减小，即其波动幅度减小，原因是由于节点9、10和14的无功补偿起到的抑制电压波动的作用。节点电压、临界电压和节点负荷裕度期望值均增大，电压稳定性提高。

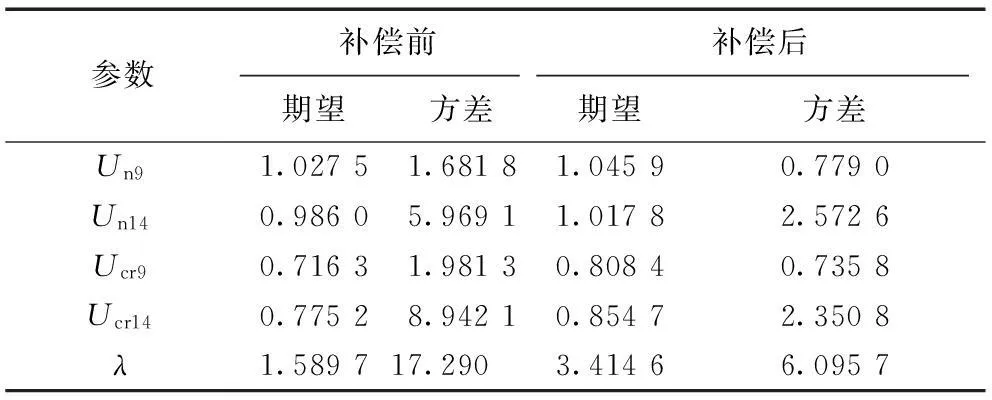
表5　期望和方差比较

注：方差数量级为(10-4)

5结论

为解决风光出力相关性问题，减小不确定因素对风光出力的影响，本文采用Copula函数和非参数核密度估计法建立风光出力联合概率分布，并通过离散化和双重积分得出节点电压、负荷裕度和临界电压的离散概率分布，采用半不变量和Gram-Charlier级数拟合负荷裕度和临界电压的分布曲线。以IEEE14系统接入风电场和光伏电站为例进行测试，与蒙特卡洛法和随机响应面法进行比较，验证了所提方法的正确性和精度。以秩相关系数衡量风光出力相关性，分析不同相关性对负荷裕度的影响，忽略相关性将对计算结果产生较大误差。以节点电压均值、方差、临界电压均值和负荷裕度均值为指标，分析风光接入对系统电压稳定的影响，得出风光接入后系统电压稳定性降低。对系统薄弱节点进行无功补偿，可以减小风电场和光伏电站接入点电压波动，提高系统电压稳定性。

参考文献：

[1] 张丽英，叶廷路，辛耀中．大规模风电接入电网的相关问题及措施[J]．中国电机工程学报，2010，30(25)：1-9．

[2] 迟永宁，刘燕华，王伟胜，等．风电接入对电力系统的影响 [J]．电网技术，2007，31(3)：77-81．

[3] Conti S，Raiti S．Probabilistic load flow using Monte Carlo techniques for distribution networks with photovoltaic generators [J]．Solar Energy，2007，81(12)：1473-1481．

[4] 蔡德福，石东源，陈金富．基于多项式正态变换和拉丁超立方采样的概率潮流计算方法 [J]．中国电机工程学报，2013，33(13)：92-100．

[5] Chen Y，Wen J，Cheng S．Probabilistic load flow method based on Nataf transformation and Latin hypercube sampling [J]．Sustainable Energy，IEEE Transactions on，2013，4(2)：294-301．

[6] Zhang P，Lee S T. Probabilistic load flow computation using the method of combined cumulants and Gram-Charlier expansion [J]. Power Systems，IEEE Transactions on，2004，19(1)：676-682．

[7] 董雷，程卫东，杨以涵．含风电场的电力系统概率潮流计算 [J]．电网技术，2009，33(16)：87-91．

[8] 高元海，王淳．基于全概率公式的含风电配电系统概率潮流计算 [J]．中国电机工程学报，2015，35(2)：327-334．

[9] 柳杰，刘志刚，孙婉璐．含风电场电力系统电压稳定性概率评估及其在无功优化中的应用 [J]．电网技术，2012，36(11)：134-139．

[10] 胡丽娟，刘科研，盛万兴，等．含随机出力分布式电源的配电网静态电压稳定快速概率评估方法 [J]．电网技术，2014，38(10)：2766-2771．

[11] 王敏，丁明．考虑分布式电源的静态电压稳定概率评估 [J]．中国电机工程学报，2010，30(25)：17-22．

[12] 鲍海波，韦化．考虑风电的电压稳定概率评估的随机响应面法 [J]．中国电机工程学报，2012，32(13)：77-85．

[13] 赵继超，袁越，傅质馨，等．基于Copula理论的风光互补发电系统可靠性评估[J]．电力自动化设备，2013，33(1)：124-129．

[14] 颜伟，任洲洋，赵霞，等．光伏电源输出功率的非参数核密度估计模型[J]．电力系统自动化，2013，37(10)：35-40．

[15] Papaefthymiou G，Kurowicka D．Using copula for modeling stochastic dependence in power system uncertainty analysis [J].Power Systems, IEEE Transactions on, 2009，24(1)：40-49．

[16] Parzen E．On estimation of a probability density function and mode [J]．The annuals of mathematical statistics，1962：1065-1076．

[17] 王俊，蔡兴国，季峰．基于Copula理论的相关随机变量模拟方法[J]．中国电机工程学报，2013，22(33)：75-82．

[18] Braun M，Stetz T，Reimann T，et al．Optimal reactive power supply in distribution networks-technological and economic assessment for PV- systems[C]//European Photovoltaic Solar Energy Conference (EU PVSEC 2009), Hamburg (Germany). 2009.

[19] 郭效军，蔡德福．不同级数展开的半不变量法概率潮流计算比较分析[J]．电力自动化设备，2013，33(12)：85-90．

Probabilistic Analysis of Voltage Stability for Power System Considering Correlativity of Wind-solar Output

LU Jinling，HE Zhenmin，WEI Fangyuan，JIA Jingran

(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)

Abstract:In this paper, a discretized joint probability distribution model of active power output, in which the correlativity among wind farm and PV plant was taken into account, was established using Copula theory and Kernel Density Estimation (KDE). Performing Continuous Power Flow (CPF) calculation according to different discrete segments and the discrete probability distribution of the node voltage, system load margin and critical voltage was established. In addition, the probability distribution function of the node voltage, load margin and critical voltage were obtained by using Gramm-Charlier series expansion method. The IEEE14 bus sample system including wind farm and PV plant was used for testing the proposed method. Based on the indicators aforementioned, the system voltage stability was analyzed and reactive compensation was put forward to improve voltage stability. Finally, the results verify the correctness and effectiveness of the proposed method compared with the Monte Carlo simulation and stochastic response surface method.

Key words：voltage stability; wind farm; photovoltaic power plant; correlativity; reactive power compensation

作者简介：卢锦玲(1971-)，女，副教授，研究方向为电力系统运行、分析与控制；何振民(1989-)，男，硕士研究生，研究方向为电力系统电压稳定性分析；魏方园(1990-)，男，硕士研究生，研究方向为电力系统运行、分析与控制；贾静然(1990-)，女，硕士研究生，研究方向为电力系统运行、分析与控制。

中图分类号：TM614；TM743

文献标识码：A

文章编号：1007-2691(2016)01-0058-07

收稿日期：2015-05-04.

doi:10.3969/j.ISSN.1007-2691.2016.01.10