技术站列车编组计划的综合优化方法
肖 杰,林柏梁,王家喜,刘 畅,李 建
(北京交通大学 交通运输学院,北京 100044)
优化技术站的列车编组计划能够充分发挥技术站作业能力,提高车流组织效率。根据车流组织形式,技术站列车编组计划包括单组列车编组计划和分组列车编组计划。
既有的研究成果中,针对单组列车编组计划的主要有:林柏梁[1]等人构建了基于最远站法则的列车编组计划的双层模型,上层确定列车到发站,下层根据流量平衡确定车流改编方案,并采用模拟退火算法对模型进行了求解;许红[2]等人综合车站改编能力、调车线容车数等限制条件构建单组列车编组计划,使所耗费的总车小时最少。张震[3]研究了技术直达列车编组计划优化方法,提出了基于车流无改编通过支点站的最大次数及有利性判别条件式。
针对分组列车编组计划的主要有:李夏苗[4]等人利用分组列车组织快运货物运输,同时考虑了牵引条件和发车时间间隔限制的条件,以运输收入最大为目标,确定了经济有效的组织方式。梁栋[5]等人根据分组列车的组织特点,提出了带有阶跃函数的技术站分组列车编组计划的0-1规划模型。这些研究均没有在编组计划编制过程中同时考虑单组列车和分组列车,进行综合优化。
单组列车是货物列车最基本的组织形式,分组列车是单组列车的一种辅助或附属形式。相比于单组列车,分组列车可以减少沿途技术站的调车作业量,但却需要技术站具有更多的调车线和较大的改编能力。因此,在优化技术站列车编组计划时应综合考虑单组列车和分组列车,发挥各自优势,从而提高运输效率。本文基于这种情况,首先在给定技术站的技术参数、车流量和车流径路的条件下,构建单组列车编组计划优化模型;在此基础上,分别计算合并式分组列车和衔接式分组列车的车小时消耗;以最大限度地降低技术站总的车小时消耗为目标,引入阶跃函数设置开行分组列车的条件,建立包括单组列车和分组列车的编组计划综合优化模型。采用遗传算法求解单组列车编组计划优化模型,并将计算结果作为已知条件,采用遍历算法求解技术站编组计划综合优化模型,得到综合效益更佳的技术站列车编组计划。并用实例证明本文所建立模型和算法的合理性和有效性。
1 单组列车编组计划优化模型
构建技术站单组列车编组计划需要考虑技术站的改编能力和调车线数量等约束条件,确定列车开行方案,实现车流组织总成本最小。
1.1 模型前提假设
首先做如下设定:任意2个技术站之间的运量均为已知;所有车流径路以《全国铁路货物运输特定计费径路》为准,即所有车流径路均为已知[6];去向相同的各支车流在某站合并之后,就被视作1股车流,在运送的过程中不能被拆散;相邻车站之间的车流以小运转列车或者直通方式运送,即所有相邻车站均存在直达去向。
1.2 单组列车编组计划优化模型
定义S为路网上车站的集合;i,j,k,e,y等泛指路网上任一车站。以i,j,k为例定义如下变量:Yi为i站后方车站的集合;Ei为i站前方车站的集合;Ci为i站的集结参数,Hi为i站调车线的数量;Dij为i站到j站所经过的技术站集合;aij为i站到j站的始发直达车流量;mij为i站到j站的列车平均编成辆数;fij为i站到j站的实际车流量,不仅包括从i站到j站的固有的车流量aij,还有来自i站后方且经i站改编的车流量;gij为i站到j站去向吸引的车流强度;Fk为技术站k的改编车流量;τk为技术站k进行车辆改编的时间消耗;Mk为技术站k的最大改编能力;γk为技术站k改编能力利用系数。
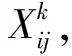
根据车流不可分割原则,一股车流在某技术站要么无改编通过,要么全部改编,不存在部分改编情况,即从i站到j站的车流必须满足车流不可分割约束条件,即
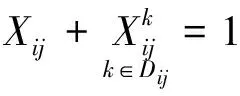
(1)
若i站到j站的车流在途中k站进行改编,则必须满足i站到j站存在近程直达去向的限制条件,即
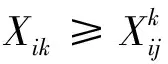
(2)
技术站k的改编车流量Fk必须满足其改编能力限制条件[7],即
Fk≤Mkγk∀k∈S
(3)
其中,


编发列车占用的调车线数量应满足该站的调车线数量约束条件[8],即
φ(gij)≤Hi∀i∈S
(4)
其中,
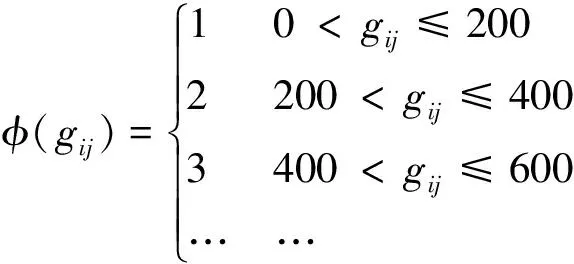
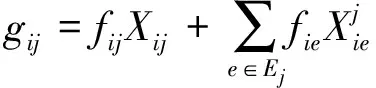
式中:φ(gij)为1个阶跃函数,反映调车线使用情况,本文假设1条调车线1昼夜可容纳200车,因此每1个编组去向中每增加200车就需要增加1条调车线。
以编组去向消耗的技术站总车小时最小为目标函数,构建的单组列车编组计划优化模型为
s.t. 式(1)—式(4)
(5)
2 分组列车的技术效益分析
2.1 分组列车的利弊分析
分组列车由2个及其以上不同到站的车组组成,并且要在沿途技术站至少进行1次换挂作业。分组列车包括基本组和补轴组,其中到达列车终点站及其以远的车组为基本组,到达沿途技术站换下和挂上的车组为补轴组。
与单组列车相比,分组列车具有以下优势[8]。①减少货物列车在编成站的集结时间。分组列车集结时,基本组和补轴组都不需达到列车编成辆数就可以结束,压缩了集结时间。②减轻沿途技术站调车作业负荷。分组列车只需对摘挂车组进行改编,并不需要对整个列车改编。③加速车辆运行。分组列车免除基本组在沿途技术站的改编作业,加速列车中转。
但分组列车的组织方式较为复杂,对技术站作业要求也比较严格,主要表现在以下4个方面。①编成站设备要求高。分组列车的基本组和补轴组分线集结时需要占用较多的调车线路,同时不能混编,故编成站需要有较大的改编能力。②换挂站车流稳定。为防止列车欠轴运行甚至提前解体,要求换挂站的补轴车流稳定可靠。③要求选择换挂站时应避免纵列式且无直通场的编组站。④换挂站需要及时准备好换挂车组,以保证分组列车在站停留时间内完成换挂作业。
随着车组数量的增加,因基本组和补轴组之间的相互等待而消耗的车小时也随之增加,考虑到目前大多数编组站调车线不足等因素,分组列车的组数不应过多,并且分3组的分组列车极其罕见,因此本文仅针对双组分组列车展开研究。
2.2 分组列车分类
根据分组列车的组成方式,可分为合并式和衔接式2种分组列车,如图1和图2所示,NAC,NAB,NBC为任意2个车站之间的车流,合并式分组列车是将2支或者多支单组列车合并为1支分组列车,而衔接式分组列车是将2支或者多支单组列车连接为1支分组列车。这2种情形都是分组列车代替单组列车,可以减少单组列车改编方案中列车到达站数目,但是代替是否有利,还需通过技术经济比较确定。

图1 合并式分组列车

图2 衔接式分组列车
根据分组列车基本组和补轴组重量是否固定可分为不固定车组重量和固定车组重量。这里重量均以车辆数进行描述,如图3和图4所示,当摘解车流不大于补挂车流,即方向上车流量递增NBC≥NAB时,采用不固定车组重量的分组列车,将换挂站多出的补轴车流NBC-NAB开行单组列车;反之将开行固定车组重量的分组列车,将编成站多出的补轴车流NAB-NBC开行单组列车,这种形式的分组列车可以避免基本车组在换挂站因等待补轴车组集结而产生延误,或者无车流补轴而提前解体[9]。
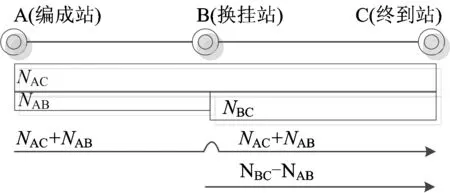
图3 不固定车组重量的分组列车
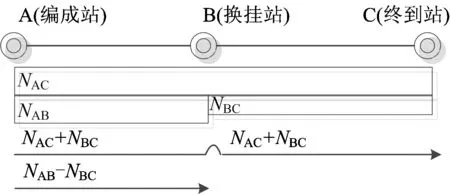
图4 固定车组重量的分组列车
2.3 分组列车车小时消耗的计算
本文针对车组重量固定和不固定的合并式分组列车和衔接式分组列车分别计算其车小时的消耗。为了叙述简便,上图中远程车流NAC作为分组列车的基本车组用NJ表示,短程车流NAB和NBC作为分组列车的补轴车组,分别用NZ和NG表示。
2.3.1合并式分组列车车小时消耗的计算
2.3.1.1不固定车组重量(即NG≥NZ)
1)编成站
不固定车组重量的合并式分组列车在编成站的车小时消耗主要包括车辆集结车小时和编组作业车小时。
(6)
式中:CA为A站的集结系数;m为列车平均编成辆数。
(7)
2)换挂站
不固定车组重量的合并式分组列车在换挂站的车小时消耗包括集结车小时消耗、车组等待车小时消耗、调车作业车小时消耗和直通车流额外停留车小时消耗4部分。
(8)
式中:CB为B站集结系数;mB为补轴车组平均编成辆数。

(9)
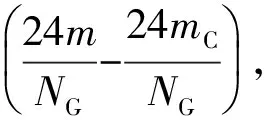
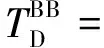
(10)
式中:mJ为基本车组平均编成辆数。
(11)

①当NG=NZ时,
(12)
②当NG>NZ时,
(13)
(14)
(4)直通车流额外停留车小时消耗ΔTZT。分组列车在换挂站的停留时间要比无改编中转列车停站时间长,所以分组列车内的直通车流NZT在换挂站1昼夜的额外停留车小时消耗ΔTZT为
ΔTZT=NZTΔtZT
(15)
式中:ΔtZT为分组列车较无改编中转列车额外停留时间。
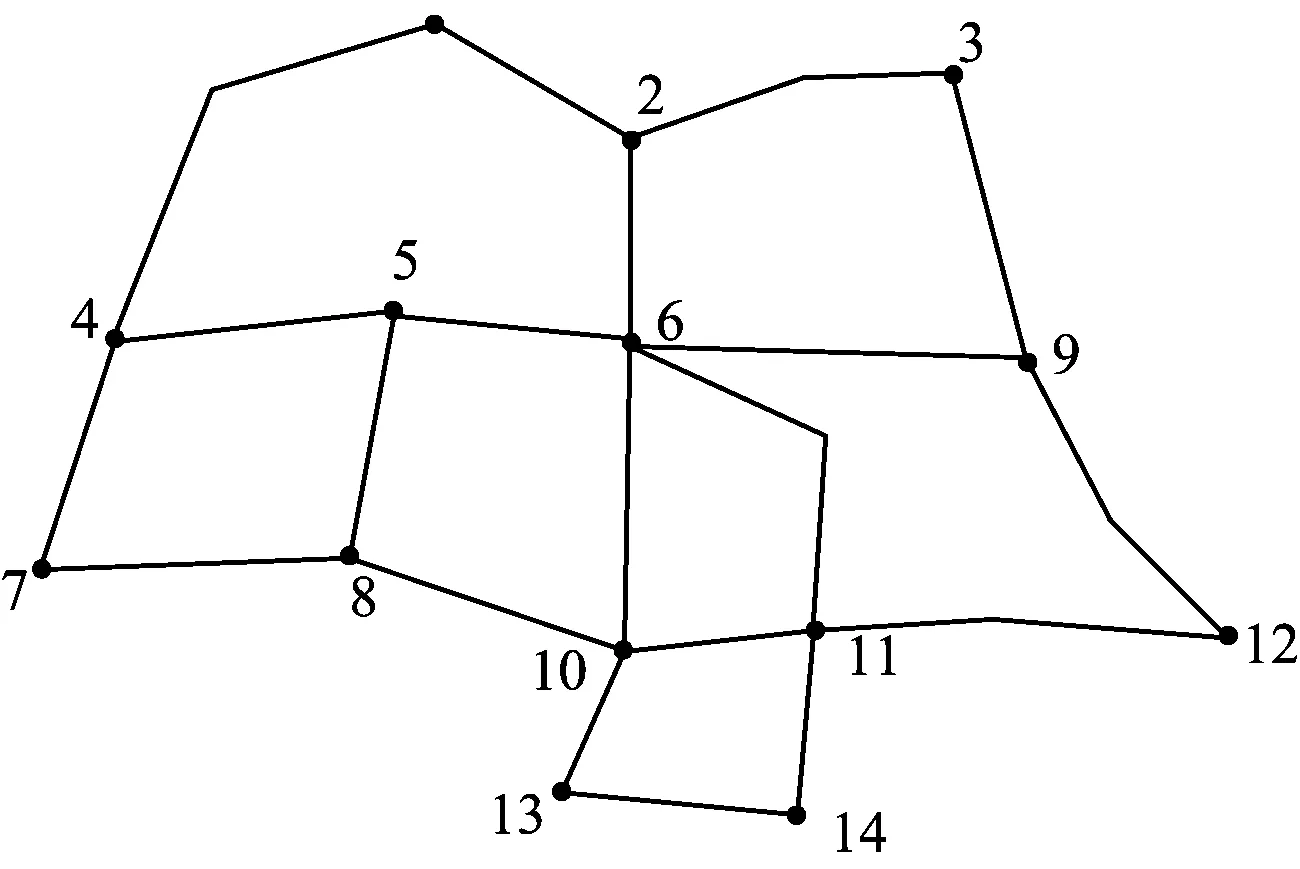
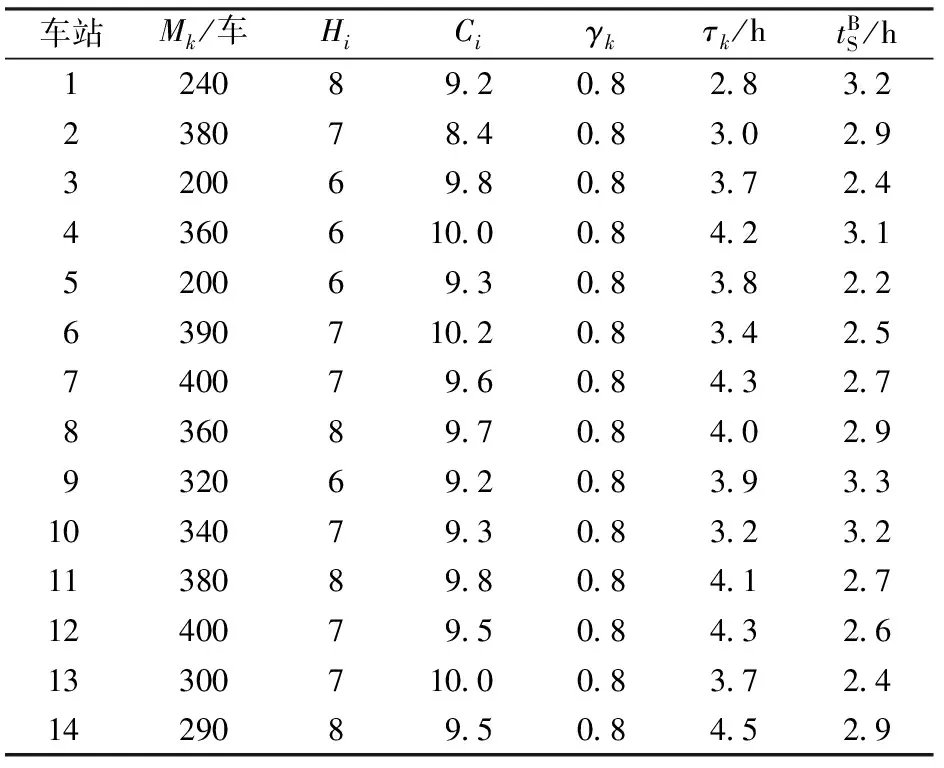
2.3.1.2固定车组重量(即NG 1)编成站 固定车组重量的分组列车在编成站的车小时消耗包含车辆集结车小时消耗、车组互相等待车小时消耗和编组作业车小时消耗。 (16) (17) (18) (19) (20) 2)换挂站 在列车换挂站,固定车组重量的分组列车的车小时消耗包括车辆集结车小时消耗、车组等待车小时消耗、调车作业车小时消耗和直通车流额外停留4部分。 (21) (22) (23) (24) (25) (4)直通车流额外停留车小时消耗ΔTZT。分组列车内的直通车流NZT在换挂站1昼夜产生的额外停留车小时消耗ΔTZT为 ΔTZT=NZTΔtZT (26) 2.3.1.3合并式分组列车1昼夜总的车小时消耗 综上,对于合并式分组列车,1昼夜总的车小时消耗TH可分为以下3种情况进行计算。 (1)当NG=NZ时, (27) (2)当NG>NZ时, (28) (3)当NG (29) 2.3.1.4合并式分组列车较单组列车的车小时节省 根据合并式分组列车1昼夜总的车小时消耗,分以下3种情况计算合并式分组列车较单组列车的车小时节省ΔTH。 (1)当NG=NZ时, (30) (2)当NG>NZ时, (31) (3)当NG (32) 2.3.2衔接式分组列车的车小时计算 衔接式分组列车与合并式相比,1昼夜增加的车小时消耗ΔTS为 (33) 再根据合并式分组列车1昼夜总的车小时消耗,可得到衔接式分组列车1昼夜总的车小时消耗TX为 TX=TH+ΔTS (34) 根据合并式分组列车较单组列车的车小时节省,得到衔接式分组列车较单组列车的车小时节省ΔTX为 ΔTX=ΔTH+ΔTS (35) 1)约束条件 (1)只有单组列车去向i站到k站与k站到j站同时存在,且与单组列车对比有车小时消耗节省,才有可能开行i站到j站去向的分组列车,则有 (36) 式中:I(x)为阶跃函数。 (2)任何1个单组去向的车流只能选择1种分组列车方案,可以是分组列车基本车组,也可以作为分组列车的补轴车组,但只能选择其中1种,则有 (37) (3)分组列车的换挂站应该避免选择没有直通场的纵列式编组站,设集合W是不能作为换挂站的技术站集合,则有 (38) 此外,分组列车换挂站应该避免选择车站能力限制的编组站,但由于分组列车方案是在最优单组列车编组方案的基础上建立起来的,此处不再考虑车站能力限制。 2)综合优化模型 综上,以列车集结和车流改编的总车小时消耗最小为目标函数,综合考虑单组列车和分组列车,在满足路网上车站设备能力和组织要求条件下,得到技术站列车编组计划综合优化模型为 (1-Xij)TX]} (39) s.t. 式(36)—式(38) 技术站列车编组计划优化问题是一个典型的NP难题,需要采用现代优化算法进行求解。本文首先采用遗传算法求解式(1)—式(5)所示的单组列车编组方案模型,得到单独开行单组列车的编组计划;在此基础上,采用遍历算法求解式(36)—式(39)所示的技术站编组计划综合优化模型,得到适合开行分组列车的方案,计算分组列车替代单组列车后车小时消耗节省情况,以是否有益于优化路网总的技术站车小时消耗为原则,确定是否开行分组列车;最终得到同时开行单组列车和分组列车的综合编组计划。由于遍历算法较为基本和简单,下面主要对遗传算法进行阐述。 遗传算法将1组随机产生的解作为初始解,为第1代种群,种群中的每个个体为1个解,称之为染色体,染色体通过选择、交叉、变异不断迭代进化生成下一代,经过若干代迭代,最后收敛于最优解。 首先确定计算参数:种群大小为D,最大代数为N,交叉概率为Pc,变异概率为Pm,随机生成初始种群Q(0),计算种群中个体适应度函数,按照遗传策略,对种群进行选择、交叉和变异,形成下一代种群,最后判断是否停止。遗传算法中使用适应度函数来度量每个解达到的优良程度。 1)编码 任意2个技术站去向变量的取值具有独立性,采用分块编码。 符号||之间是2个编码块,代表了2个技术站之间开行直达以及途中改编站。 2)种群大小及初始种群 种群大小决定了最终求得的解是否是全局最优解,如果规模太小,容易陷入局部最优,但种群规模太大,计算量将显著增加。经过试算,总群规模为20时能够满足计算的要求。初始种群按照编码块进行随机赋值产生,且赋值时满足式(1)的要求,保证初始种群都是有意义的取值。 3)适应度函数的选择 适应度函数根据目标函数选择,本文的目标函数Z为恒大于0的正数,因此适应度函数f可选择为 (40) 4)算子的确定 选择算子:遗传算法使用选择算子来对种群中的个体进行优胜劣汰操作,本文采用轮盘赌选择,根据个体的适应度函数值,并使适应度较高的个体遗传到一下代种群中的概率较大。第a代第b个个体被选择的概率Pb为 (41) 交叉算子:交叉运算使用单点交叉算子。只有1个交叉点位置,随机进行个体间两两组合,随机产生1个交叉点位置,2个个体在交叉点位置互换部分基因码,形成2个子个体。 变异概率:变异概率一般取为0.000 1~0.1,如果变异概率过大,遗传算法将变为随机搜索。本文使用的变异概率为0.001。 5)罚函数的设置 目标函数的限制条件中存在不等式条件,需要将其转化为等式约束条件,需要在目标函数中设置罚函数。罚数值应充分大,因此选择值为100 000。 6)终止规则 算法通过遗传代数控制终止操作,这也是遗传算法的通用终止规则。 以我国东北地区局部铁路网络为例,图5中有14个车站[11],对提出的技术站单组列车编组方案和分组列车开行方案优化模型及算法进行验证。各技术站之间的原始车流数据及各技术站的改编参数见表1和表2,分组列车相关参数见表3。 图5 路网结构示意图 表1 技术站间车流量 利用遗传算法求解单组列车编组计划优化模型,遗传算法运行50~150代时,每代最小值和每代平均值均在一个相对小的区间内变动,且目标函数值远小于罚数,因此运行到150代停止时,认为结果已经收敛到最优,得到单组列车编组方案车小时消耗最小值为157 651.84车小时。以优化得到的单组列车编组方案为已知变量,采用遍历算法,求解技术站编组计划综合优化模型,得到共需开行18组分组列车,最终得到同时开行单组列车和分组列车时,技术站列车编组计划的车小时消耗为155 743.479车小时,比仅开行单组列车时节约1 908.361车小时。 表2 各技术站改编参数 表3 分组列车相关参数 分组列车作为一种高级的车流组织形式,以编成站集结车小时消耗较少增加为代价,换取换挂站车小时消耗的较多节省,从而实现更好的技术经济效益。但开行分组列车较为复杂,相应的技术作业条件要求也较为严格,需与单组列车相互配合才能实现最大经济效益。鉴于此,本文提出了1种同时开行单组列车和分组列车的技术站列车编组计划综合优化方法。首先只考虑开行单组列车情况,以技术站的总车小时消耗最小为目标,建立单组列车编组计划规划模型。然后分别分析合并式分组列车和衔接式分组列车的车小时消耗,并对其相对于单组列车节省的车小时消耗进行计算。以最大限度地降低技术的站总车小时消耗为目标,引入阶跃函数设置开行分组列车的条件,建立同时开行单组列车和分组列车的技术站编组计划综合优化模型。采用遗传算法求解单组列车编组计划优化模型,然后以计算结果为已知条件,采用遍历算法求解综合优化模型,得到综合效益更佳的技术站列车编组计划。最后通过1个实例计算证明,采用本文提出的模型和算法能够快速、便捷地获得1个同时开行单组列车和分组列车的技术站综合列车编组计划,且综合列车编组计划能有效降低技术站的总车小时消耗。 [1]林柏梁, 田亚明, 王志美. 基于最远站法则的列车编组计划优化双层规划模型[J]. 中国铁道科学, 2011, 32(5):108-113. (LIN Boliang, TIAN Yaming, WANG Zhimei. The Bi-Level Programming Model for Optimizing Train Formation Plan and Technical Station Load Distribution Based on the Remote Reclassification Rule [J]. China Railway Science, 2011, 32(5):108-113. in Chinese) [2]许红, 马建军, 龙昭, 等. 技术站单组列车编组方案模型与计算方法的研究[J]. 铁道学报, 2006, 28(3):12-17. (XU Hong, MA Jianjun, LONG Zhao, et al. Study on the Model and Algorithm of the Formation Plan of Single Group Trains at Technical Service Stations [J]. Journal of the China Railway Society, 2006, 28(3):12-17. in Chinese) [3]张震. 单组技术直达列车编组方案的最优化理论和方法[J]. 铁道运输与经济, 1979(1):43-53. (ZHANG Zhen. The Optimization Theory and Method for One-Block Train Formation Plan [J]. Railway Transport and Economy, 1979(1):43-53. in Chinese) [4]李夏苗, 卢红岩. 快运货物列车编组方案的优化[J]. 中国铁道科学, 2004, 25(2):117-120. (LI Xiamiao, LU Hongyan. Optimization of Train Formation Diagram of Express Freight [J]. China Railway Science, 2004, 25(2):117-120. in Chinese) [5]梁栋, 林柏梁. 技术站分组列车编组计划的优化理论及模型研究[J]. 铁道学报, 2006, 28(3):1-5. (LIANG Dong, LIN Boliang. Study on the Theory Model of the Optimal Train Formation Plan of Multi-Block Trains at Technical Service Stations [J]. Journal of the China Railway Society, 2006, 28(3):1-5. in Chinese) [6]田亚明. 铁路网编组站改编能力配置优化研究[D]. 北京:北京交通大学, 2012:28-29. (TIAN Yamin. Railway Marshalling Yards Reclassifying Capability Configuration Optimization [D]. Beijing: Beijing Jiaotong University, 2012:28-29. in Chinese) [7]LIN Boliang, WANG Zhimei. Optimizing the Freight Train Connection Service Network of a Large-Scale Rail System[J]. Transportation Research Part B, 2012(46):649-667. [8]陈崇双, 王慈光, 杨运贵, 等. 不确定条件下开行固定车组重量分组列车适用条件研究[J]. 铁道学报, 2011, 33(12):1-8. (CHEN Chongshuang, WANG Ciguang, YANG Yungui, et al. Research on Applicable Operation Conditions of Multi-Block Train with Fixed Weight under Uncertainty [J]. Journal of the China Railway Society, 2011, 33(12):1-8. in Chinese) [9]杨浩. 铁路运输组织学[M]. 2版.北京:中国铁道出版社, 2006:248-253. [10]王慈光. 关于固定车组重量的分组列车车小时消耗的计算[J]. 西南交通大学学报, 1985(4):85-92. (WANG Ciguang. The Computation of Wagon-Hour Consumption for Multi-Group Technical through Trains with Fixed-Weight Groups [J]. Journal of Southwest Jiaotong University, 1985(4):85-92. in Chinese) [11]纪丽君, 林柏梁, 乔国会, 等. 基于多商品流模型的铁路网车流分配和径路优化模型[J]. 中国铁道科学, 2011, 32(3):107-110. (JI Lijun, LIN Boliang, QIAO Guohui, et al. Car Flow Assignment and Routing Optimization Model of Railway Network Based on Multi-Commodity Flow Model [J]. China Railway Science, 2011, 32(3):107-110. in Chinese)

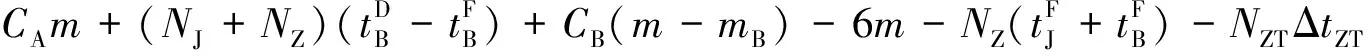
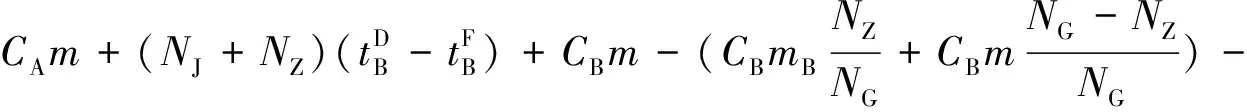
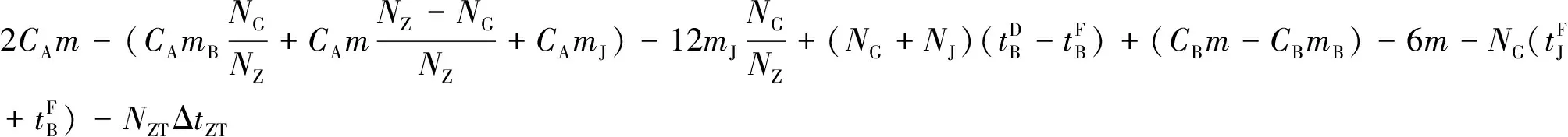
3 技术站列车编组计划综合优化模型
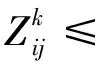
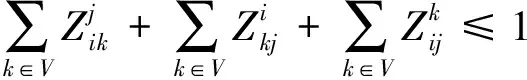
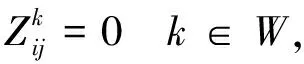
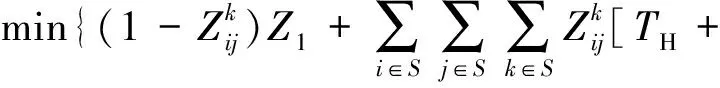
4 求解算法
5 算例分析

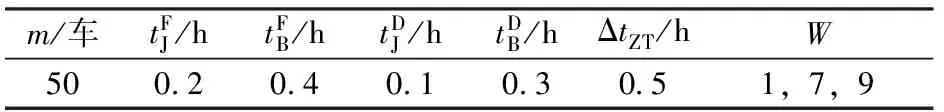
6 结 论

