城际铁路列车运行图稳定性仿真分析

马　驷,邓云霞

(1.西南交通大学 交通运输与物流学院，四川 成都　610031；2.西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都　610031)

因为列车在运行过程中会受到外界和内部的各种干扰，故为了确保列车运行图的稳定性，需要在编制的列车运行图中通过设置列车运行图冗余时间来吸收列车受干扰而引起的晚点。关于列车运行图冗余时间的研究，国内外学者分别从晚点列车传播规律[1]、区间运行时分偏离[2]、优化模型和计算机仿真[3-5]等方面展开，并多是在某一稳定性水平下设置合理的冗余时间，而较少研究列车运行图冗余时间布局对列车运行图稳定性的影响。鉴于城际铁路主要服务于通勤、公务、商务等客流，对列车的准时性和实效性要求较高，故本文以广深城际铁路为背景，通过MATLAB软件编程并用给定的评价指标对列车运行图的稳定性进行仿真分析，研究列车运行受到干扰情况下采用不同的列车停站方案及对应的不同列车运行图冗余时间布局对列车运行图稳定性的影响，为编制列车运行图提供参考。

1　影响列车运行图稳定性的因素

列车运行图稳定性是衡量列车运行受到干扰后恢复按图行车能力的指标，用于描述列车按图行车的稳定程度。对于某一具体线路，列车运行图的稳定性主要取决于列车运行图冗余时间的布局、列车停站方案和列车运行受到的干扰。

1)列车运行图冗余时间的布局

列车运行图冗余时间(以下简称冗余时间)是指实际铺画在列车运行图上的列车区间运行时分、列车停站时分、列车追踪间隔时分和车站间隔时间等图定作业时分与标准作业时分之间的差值[6]。冗余时间的布局是否合理将直接影响列车运行图的稳定性。冗余时间设置过少，会增加晚点列车的数量和晚点时间；而冗余时间设置过多，又会降低列车运行图的通过能力和旅行速度。冗余时间按布局方式可分为纵向布局(指将冗余时间布置在列车区间运行时分和列车停站时分内)和横向布局(指将冗余时间布置在列车运行线间隔时分内)2种。

2)列车停站方案

列车停站方案是指在列车等级、列车开行对数、列车运行区段等确定之后，根据客流需求和列车的协调配合情况确定的各列车停站序列。本文针对城际铁路特点选择规格化停站、按比例停站、站站停等3种停站方案为研究对象。

3)列车运行干扰

由于列车在运行过程中会受到来自外界和铁路系统内部的各种干扰，使得列车的实际运行时分与图定运行时分有一定的偏差，本文假定这种偏差服从左偏的β函数分布[7]，并根据广深线的数据资料得到β函数中各参数的取值，再用舍选法[8]随机生成服从β函数分布的列车运行干扰时间方案。

2　列车运行图稳定性的评价指标

本文采用如下指标评价列车运行图的稳定性。

(1)按图定时间到达终点站(正点到达)的列车数量与图定到达终点站的列车数量m之比，简称终到列车正点率Pzd，可表示为

(1)

式中：ai为0—1变量；i和m分别为图定到达终点站列车的编号和列车数量，i=1，2，…，m；t晚(i,n)为列车i在终点站n的晚点时间，min；n为终点站的编号，也是自始发站开始、到终点站结束，列车运行图上标示出的车站个数。

(2)

式中：j为车站的编号，j=1，2，…，n；t晚(i,j)为列车i在车站j的晚点时间。

(3)

(4)在一定的通过能力利用率和列车晚点时间概率分布条件下，通过设置在列车运行图中的冗余时间，可以使晚点列车在到达终点站或之前恢复正点运行的列车数与晚点列车数之比，简称晚点列车恢复率Phf，可表示为

(4)

式中：Nzd为完全按图定时刻运行列车的总数。

3　列车运行图的稳定性仿真

本文以广深线列车运行图中某一时段下行16列列车的运行图为例，仿真分析这16列列车在加载不同随机干扰时间下采用不同冗余时间布局对其运行图稳定性的影响。为了确保仿真结果的准确性，对每种冗余时间布局均加载20种随机生成的干扰时间方案，以取得的各运行图稳定性评价指标的平均值作为其仿真结果。

3.1　规格化停站方案下基于冗余时间布局的仿真

采用规格化停站方案，分析冗余时间纵向和横向布局对列车运行图稳定性的影响，从而得到对于规格化停站方案而言最优的冗余时间布局方案。所谓规格化停站方案是指以列车交错停站的方式尽可能地紧密铺画列车的运行线，如图1所示。

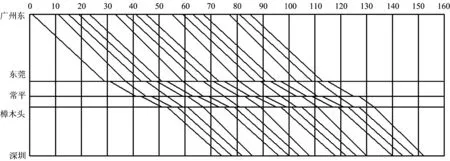
图1　规格化停站方案下的列车运行图

3.1.1冗余时间纵向布局的仿真

在不考虑冗余时间横向布局的前提下，通过改变冗余时间的纵向布局，仿真分析冗余时间纵向布局对图1所示列车运行图稳定性的影响。

1)纵向布局下冗余时间总量的影响

运用MATLAB软件，为每列车加载的随机总干扰时间为4～6 min，并按照纵向布局相应地为每列车设置的冗余时间总量(即区间运行冗余时间与停站冗余时间之和)分别为4，5和6 min；然后分别采用均衡分布、逐渐增加、最后集中3种冗余时间设置方案，仿真计算对应的列车运行图稳定性评价指标，由此得到这3种方案对应的60组仿真结果，对其取平均值，得到纵向布局下不同冗余时间总量的仿真结果，见表1。

表1　纵向布局下不同冗余时间总量对应的仿真结果

2)纵向布局下停站冗余时间总量的影响

在停站冗余时间分别取0，1，2和3 min的4种方案下，对应的区间运行冗余时间分别取6，5，4和3 min，则仿真计算得到这4种方案的列车运行图稳定性评价指标，见表2。由表2可知，当停站冗余时间总量为2 min时，其对应的各项指标均明显优于其他方案。这是因为受交错停站(规格化停站)的影响，停站冗余时间取3 min时不能保证该冗余时间得到充分利用；而停站冗余时间取0或1 min时，又不能很好地吸收列车晚点对后续列车的影响，导致终到列车正点率不高。因此，在冗余时间总量取6 min的条件下停站冗余时间取2 min、区间运行冗余时间取4 min为最佳。

表2　纵向布局下停站冗余时间总量对应的仿真结果

3)停站冗余时间布局的影响

在停站冗余时间总量取2 min的条件下，按照将该冗余时间集中设置在某一车站上的方案和在2个车站上各设置1 min的方案考虑，仿真计算这2种方案的列车运行图稳定性评价指标，见表3。由表3可知，将2 min的停站冗余时间拆分设置在2个车站上得到的列车运行图稳定性评价指标明显优于集中设在1个车站上时。因此，应将2 min的停站冗余时间拆分设在2个车站上，这样可更好地消除各种干扰对列车正点运行的影响；而且进一步的仿真计算结果还表明，将2 min的停站冗余时间拆分设置在不相邻的2个车站上时得到的列车运行图稳定性评价指标更佳。

表3　不同停站冗余时间布局对应的仿真结果

4)区间运行冗余时间布局的影响

在停站冗余时间总量取2 min且拆分设置在2个车站上的条件下，对4 min的区间运行冗余时间分别采用均匀分布、逐渐增加、最后集中的3种布局方案，进行仿真计算，结果见表4。由表4可知，采用逐渐增加的区间运行冗余时间布局方案所得到的列车运行图稳定性评价指标最佳。其原因在于各种干扰对列车正点运行的影响具有累加性，若冗余时间的布局也按这种逐渐递增的规律设置，则不但可以提高冗余时间的利用率，还可以充分吸收各种干扰对列车正点运行带来的影响。

表4　不同区间运行冗余时间布局对应的仿真结果

综上所述，最优的冗余时间纵向布局方案为：分配给每列车的冗余时间为6 min，其中，将2 min的停站冗余时间拆分设置在2个车站上，将4 min的区间运行冗余时间按照逐渐增加的布局方案设置。按此冗余时间纵向布局方案得到广深城际铁路列车运行图的冗余时间纵向布局方案，见表5。

表5　广深城际铁路列车运行图的冗余时间纵向布局方案

3.1.2冗余时间横向布局的仿真

在冗余时间纵向布局按表5考虑的前提下，对于冗余时间横向布局采用均匀设置和分组设置2种方式，仿真分析冗余时间横向布局对图1所示列车运行图稳定性的影响。

1)冗余时间横向均匀设置的影响

冗余时间横向均匀设置是指在相邻的两追踪运行列车之间均设置相同的冗余时间。横向均匀设置的冗余时间分别取0，1和2 min，仿真计算对应的列车运行图稳定性评价指标，结果见表6。由表6可知，在相邻两列车之间设置1 min的冗余时间就能得到较好的列车运行图稳定性评价指标，若再继续增加冗余时间，不但对提高列车正点率和减少列车晚点时间的作用不大，反而会降低列车运行图的通过能力。假设按每天可用时间为1 000 min计算可铺画的列车总对数，则每在两列车间增加1 min的冗余时间，就会减少通过能力20对左右。

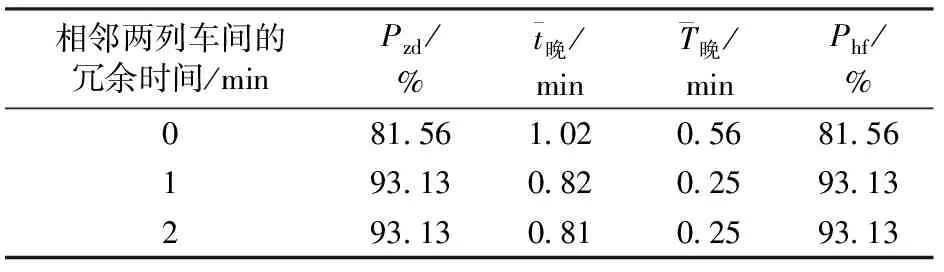
表6　冗余时间横向均匀设置对应的仿真结果

2)冗余时间横向分组设置的影响

将某个方向某个时间段的列车群划分为若干组，每组内的相邻两追踪列车之间不设置冗余时间，而在相邻两列车组之间设置相同的冗余时间，这种冗余时间的横向布局方式即为冗余时间横向分组设置。仍以广深线列车运行图中某一时段下行列车运行图为例，采用冗余时间横向分组设置，仿真计算对应的列车运行图稳定性评价指标，结果见表7。由表7可知，在相邻两列车组间设置1 min的冗余时间即可得到较好的列车运行图稳定性评价指标，而再继续增加相邻两列车组间的冗余时间对指标的改善幅度不大；从通过能力考虑，以4列列车为1组并在相邻两列车组间设置1 min的冗余时间为最佳的冗余时间横向分组设置方案，其原因在于以4列车为1列车组并按规格化停站方案铺画列车运行图时，通过列车组内相邻两列车间停站冗余时间与相邻两列车组间冗余时间的配合，可很好地吸收列车晚点对后续列车正点运行产生的影响。

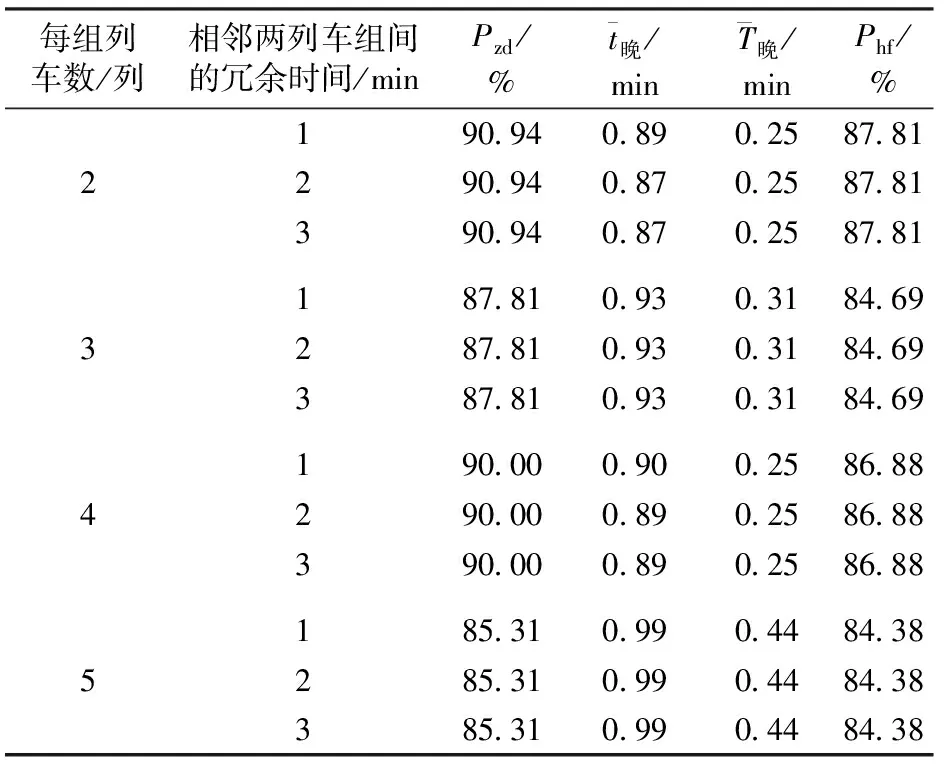
表7　冗余时间横向分组设置对应的仿真结果

由表6、表7可知，在相邻两列车组间设置1 min冗余时间的前提下，2列为1组相比4列为1组的列车组划分方案，前者的晚点列车恢复率虽高出6.25%，但通过能力降低了3.75对；因此在客流高峰期为保证较高的通过能力，宜采用后者，而在其他时段为保证较高的正点率，宜采用前者。

3.2　其他停站方案下基于冗余时间布局的仿真

除规格化停站方案外，还有按比例停站方案、站站停方案等其他停车方案。故本文同样按照3.1节的研究方法，分别在按比例停站方案和站站停方案下对冗余时间布局给列车运行图稳定性带来的影响进行仿真。受篇幅所限，仅给出仿真结果。

1)冗余时间纵向布局的仿真

在不考虑冗余时间横向布局的条件下，分别在按比例停站方案、站站停方案下对冗余时间布局给列车运行图稳定性带来的影响进行仿真，并与规格化停站方案下的仿真结果进行对比，结果是影响规律相似，得到的冗余时间纵向布局最佳方案仍是冗余时间总量取6 min，其中停站冗余时间取2 min，区间运行冗余时间取4 min；具体到本文实例也仍是采取表5的布局方案最优。但是，在站站停方案下无论冗余时间纵向布局如何设置，仍有超过80%的列车晚点，其原因在于该方案下所有列车均按最小追踪间隔运行，一旦有列车晚点，就会连带引起后续列车晚点；因此若采取站站停方案，则必须考虑冗余时间的横向布局。

2)冗余时间横向布局的仿真

在冗余时间的纵向布局均按表5所示最优方案设置的条件下，当冗余时间横向布局采用均匀设置的方式时，按比例停站方案、站站停方案与规格化停站方案下得到的仿真结果相似，且均为在相邻两列车间设置1 min的冗余时间为最佳，这样基本能保证晚点列车全部恢复正点。当采用冗余时间横向分组设置方式时，按比例停站方案与规格化停站方案下得到的仿真结果相似，在相邻两列车组间设置1 min冗余时间为最佳，不过随着列车组内列车数的增大，晚点列车的数量和晚点时间有小幅度增加；而在站站停方案下相邻两列车组间至少需要设置2 min的冗余时间，且各列车组内的列车数不得超过3列，否则列车的正点率会低于80%。

3)站站停方案下冗余时间横向布局的仿真

为了进一步分析站站停方案下冗余时间横向布局对列车运行图稳定性的影响，分别以1，2，3，…，8列列车为1组划分列车群，在相邻两列车组间设置不同的冗余时间，经仿真计算得到站站停方案下列车组内不同列车数对应的相邻两列车组间冗余时间上限(见表8)以及相邻两列车组间冗余时间取不同值对列车运行图稳定性的影响(见表9)。

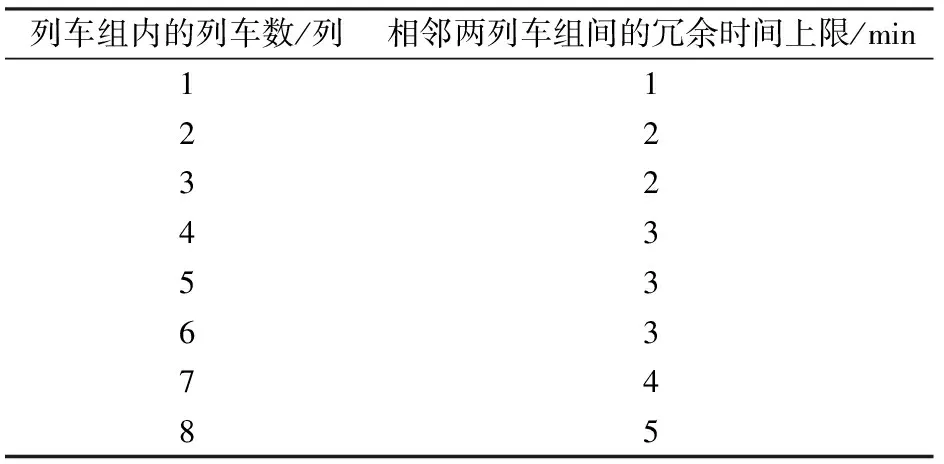
表8　列车组内不同列车数对应的冗余时间上限值

表9　站站停方案下冗余时间横向布局对应的仿真结果

由表8可知，设置的冗余时间如果超过该冗余时间上限值，即使再增加列车组间的冗余时间，基本上也难以提高列车正点率和减少列车晚点时间，反而会降低通过能力。

由表9可知，在按站站停方案和列车群不分组(亦可视为每列列车自成1组)的情况下，在相邻两列车间均设置1 min的冗余时间可保证列车的正点率达到100%；而以2列列车为1组划分列车群的情况下，若要求列车正点率达到90%或80%以上，则相邻两列车组间需要设置2或1 min的冗余时间；在以3列列车为1组划分列车群的情况下，若要求列车正点率达到80%以上，则相邻两列车组间需要设置2 min的冗余时间；显然，随着相邻两列车间平均冗余时间的增加，列车正点率不断提高，但是通过能力不断减小。

按站站停方案和在相邻两列车组间设置1 min冗余时间的条件下，列车正点率和通过能力随列车组内列车数变化的关系曲线如图2所示。由图2可见，列车正点率随着列车组内列车数量的增加而下降，且在列车正点率降至65%以后，列车正点率的下降幅度高于通过能力增加的幅度。

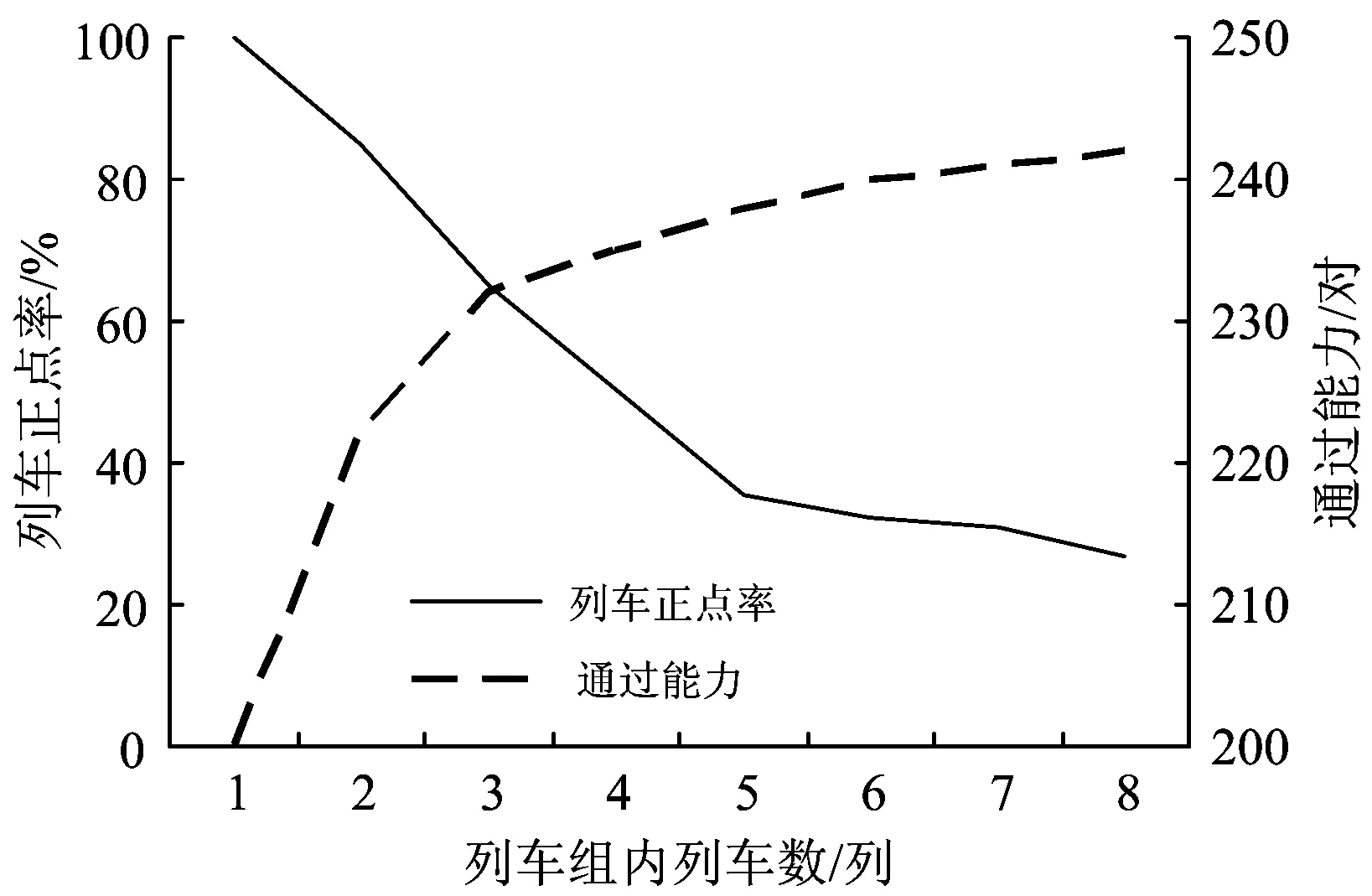
图2　站站停方案及相邻两列车间冗余时间为1 min条件下列车正点率和通过能力随列车组内列车数量的变化

4　结　论

(1)在随机干扰时间总量取4～6 min的情况下，纵向布局的冗余时间总量宜取随机干扰时间总量的最大值，且区间运行冗余时间和停站冗余时间分别取4和2 min为最佳。

(2)因列车运行干扰具有累加性，故区间运行冗余时间最好按逐渐增加方案设置，停站冗余时间则宜分设在2个不相邻的车站上。

(3)在冗余时间纵向布局按最优方案设置的条件下，冗余时间横向布局的最优方案为在相邻两列车间均设置1 min的冗余时间。

(4)在按比例停站方案和规格化停站方案下，均可采取相同的冗余时间横向布局方案；但站站停方案下采用冗余时间横向分组设置方式时，对横向布局的冗余时间需求远高于其他2种停站方案。

(5)在站站停方案下，两相邻列车间的平均冗余时间与列车正点率正相关，与通过能力负相关，即增加冗余时间会在提高列车正点率的同时，降低通过能力。

今后将针对中间站多且有列车越行等情况的其他城际铁路，进一步研究冗余时间布局对列车运行图稳定性的影响规律，并考虑将列车晚点导致后续列车连带晚点的影响纳入列车运行图稳定性的评价指标内，为编制稳定性好的列车运行图提供参考。

[1]CAREY M, CARVILLE S. Testing Schedule Performance and Reliability for Train Stations[J]. Journal of Operational Research Society, 2000,51(6):666-682.

[2]查伟雄，熊桂林. 列车区间运行时分动态特性研究[J]. 系统工程，2001，19(1) :47-51.

(ZHA Weixiong，XIONG Guilin. Study on the Dynamic Performance of the Train Running Time in the Section[J]. Systems Engineering，2001，19(1) :47-51.in Chinese)

[3]VROMANS M J. Reliability of Railway Systems[D]. Rotterdam: Erasmus University Rotterdam，2005：55-81.

[4]LUDOLF E M，SANDER M. Stochastic Delay Propagation in Railway Networks and Phase-Type Distributions [J]. Transportation Research Part B：Methodological，2007，41(2)：218-230.

[5]宁骥龙.城际客运专线列车运行图冗余时间布局优化研究[D]. 成都：西南交通大学，2013.

[6]邓鹏. 我国高速铁路列车运行图动态性能研究[D]. 成都：西南交通大学，2012.

[7]张星臣. 铁路运营线路能力储备问题的研究[D]. 北京：北方交通大学，1995：38-42.

[8]SALIMIFARD K M W. Petri Net-Based Modeling of Workflow Systems: an Overview[J]. European Journal of Operational Research，2001，134(1)：664-676.