列车属性对城市轨道交通牵引能耗的影响及列车用能效率评价

陈　垚,毛保华,柏　赟,贾文峥，李竹君

(1.北京交通大学 城市复杂系统理论与技术教育部重点实验室，北京　100044；2.交通运输部 科学研究院城市交通研究中心，北京　100029)

城市轨道交通系统能源消耗总量巨大，其中的牵引能耗是城市轨道交通系统能耗的重要组成部分，约占总能耗的50%[1]。分析牵引能耗的影响因素有助于降低牵引能耗，对节约能源、降低运营成本具有重要意义。

城市轨道交通列车的属性包括列车质量、单位基本阻力和牵引特性等。列车属性对牵引能耗的影响不容忽视。孔令洋等[1]基于电机效率对比了直线电机系统和旋转电机系统的牵引能耗。Hoyt等[2]通过建立仿真系统描述了列车编组和牵引性能对货物列车能耗的影响。刘海东等[3]采用计算机模拟的方法研究了列车质量与牵引能耗的关系。IFEU[4]根据德国不同种类列车的数据，分析了列车自重的降低对牵引能耗的影响程度。Raghunathan等[5]分别讨论了不同流线型设计对列车运行阻力和牵引能耗的影响。

以上研究分析了某一列车属性与牵引能耗的关系，但未判断各列车属性对牵引能耗的影响程度。列车用能效率由多个列车属性共同决定，某一列车属性难以判断列车用能效率情况；既有研究尚未提出1个用于刻画列车用能效率的评价指标，为实现城市轨道交通车辆节能选型提供依据。

本文通过建立城市轨道交通列车牵引能耗模型，分析影响牵引能耗的列车属性，并采用灵敏度分析的方法判断各列车属性的重要程度；提出列车用能效率评价指标，并对比不同列车的指标值与列车在同一线路和运行模式下的仿真能耗，以验证评价指标的有效性。

1　影响牵引能耗的列车属性

1.1　列车牵引能耗模型

牵引能耗是指列车在运行过程中消耗的电能，主要包括牵引系统驱动列车运行的能耗、空调照明等车载辅助设备运行的能耗(辅助能耗)及再生制动反馈回牵引电网的能耗(再生制动能耗)[6]。辅助能耗主要受车载辅助设备、气温、线路敷设方式的影响[6]，与列车属性的关系不明显；再生制动能耗不仅与列车属性有关，更多的是由列车到发时刻、列车运行过程、牵引供电电压、能量吸收装置决定[7]。

因此，本文分析牵引能耗时不考虑辅助能耗和再生制动能耗。牵引能耗为牵引工况下列车牵引系统用于牵引加速所消耗的能量。假设列车在平直线路上、牵引工况下的单位合力为

(1)

式中：c为列车单位合力，N·kN-1；F为列车牵引力，N；w为列车单位基本阻力，N·kN-1；m为列车质量，t；g为重力加速度，取9.81 m·s-2。

将列车视为1个刚性质点，根据动能、动量定理可得

(2)

式中：v为列车速度， km·h-1；t为牵引时间，h；γ为回转质量系数；ξ为加速度系数，m·s-2。

列车在牵引运行时，牵引功率为牵引供电系统的牵引电压与牵引电流的乘积，即

(3)

式中：P为牵引功率，W；Q为牵引能耗，W·h；U为牵引供电系统的牵引电压，V；I为牵引电流，A。

因此，由式(1)—式(3)可知，列车的牵引能耗与速度的微分关系可表述为

(4)

则列车牵引能耗模型为

(5)

1.2　影响牵引能耗的列车属性

列车牵引能耗模型表明，在平直线路上列车的牵引能耗由被积函数UImg/[ξ(F-wmg)]与被积变量v决定。在速度变化相同时，即在相同的列车速度曲线下，被积函数UImg/[ξ(F-wmg)]将决定牵引能耗的大小。

其中，牵引电压由牵引供电系统决定，与列车属性无关。加速度系数取决于回转质量系数，因列车类型而异；但各列车的加速度系数相差甚小，对牵引能耗的影响可以忽略不计，本文统一取平均值120 m·s-2。列车牵引力与牵引电流相关联，由牵引电机效率决定。牵引电机效率可以表征为列车的牵引力与速度的乘积除以牵引电压与牵引电流的乘积。因此，影响牵引能耗的列车属性主要有列车质量、单位基本阻力和牵引电机效率。

2　列车属性影响牵引能耗的灵敏度分析

下面采用灵敏度分析的方法计算牵引能耗的变化，分析单一属性变化导致牵引能耗变化的程度，从而判断各属性的重要程度。为方便计算，令a=F/mg表示列车单位牵引力，N·kN-1，Q′表示不同列车属性变化后的牵引能耗。

1)列车质量

当列车质量提高x1%时，其牵引能耗模型可表示为

(6)

显然可得

(7)

而当列车质量下降x2%时，同理可得

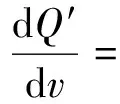
(8)

因此，当列车速度曲线固定，列车质量提高(或下降)时，其牵引能耗上升(或下降)的比例大于列车质量上升(或下降)的比例。

2)单位基本阻力

当单位基本阻力提高x3%时，列车的牵引能耗模型可表示为

(9)

当x3<(100a/w-200)时，通过不等式变形可得

(10)

而当单位基本阻力下降x4%时，在x4>(200-100a/w)时，同理可得

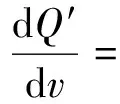
(11)

城市轨道交通列车的速度较低，其单位基本阻力较小，则a远大于w。因此，当列车速度曲线固定、单位基本阻力提高(或下降)时，列车牵引能耗上升(或下降)的比例小于单位基本阻力提高(或下降)的比例。

3)牵引电机效率

当牵引力不变、牵引电流上升x5%时，列车的牵引能耗模型可表示为

(12)

由式(12)可知，牵引电机效率下降的比例为x5/(100+x5)时，列车的牵引能耗上升x5%。因此，当列车速度曲线固定、牵引电机效率下降时，列车牵引能耗上升的比例大于牵引电机效率下降的比例。

而当牵引力不变、牵引电流下降为x6%时，列车的牵引能耗可表示为

(13)

由式(13)可知，牵引电机效率提高的比例为x6/(100-x6)时，列车的牵引能耗下降x6%。因此，当列车速度曲线固定、牵引电机效率提高时，列车牵引能耗下降的比例小于牵引电机效率提高的比例。

综上分析可知，上述3个列车属性中，列车质量对牵引能耗的影响程度最大；单位基本阻力的影响程度最小，其原因是城市轨道交通列车速度较低导致列车运行过程所受到的阻力相对较小；牵引电机效率对牵引能耗的影响程度会随牵引电机效率的大小而变化，牵引电机效率越大，其对牵引能耗的影响程度越小。

3　列车用能效率评价

因为列车的型号不同，其用能效率也不同，所以将牵引能耗模型中的被积函数UImg/[ξ(F-wmg)]定义为“列车用能效率特征值”，以评价列车用能效率。

列车用能效率特征值综合考虑了影响牵引能耗的各列车属性。由列车的牵引能耗与速度的微分关系可知，列车用能效率特征值为单位速度变化所引起的牵引能耗变化值。从牵引能耗的角度来看，列车用能效率特征值反映的是列车在平直线路上运行时提高单位速度所需要的牵引能耗。显然，列车用能效率特征值越高，列车在相同加速过程中所消耗的电量越多，即列车的用能效率越低。由牵引能耗模型可知，列车在平直线路上采用相同速度曲线运行时，其牵引能耗只取决于列车用能效率特征值。在相同线路与运行过程下，列车用能效率特征值越大，列车的牵引能耗越高。因此，列车用能效率特征值可以评价列车的用能效率。

列车用能效率特征值是随速度变化而变化的变量。因此，为评价列车在区间上的用能效率，应该以列车速度曲线[8]为基础，采用列车用能效率特征值的平均值来评价列车用能效率。

列车在长大区间运行时，其速度曲线如图1所示。图中：v1为线路限速；v2为惰行工况结束时(制动工况开始)的速度。在起动加速阶段，列车采用最大牵引力牵引，并逐渐接近限速(v1)。途中运行阶段，列车在一定的速度(v1～v2)范围内交替使用惰行、牵引工况运行，直至接近车站制动停车。

列车在短区间运行时，其速度曲线如图2所示。由于站间距离短，列车采用“牵引—惰行—制动”的策略运行。

图1　长大区间下列车速度曲线

图2　短区间下列车速度曲线

由图1可知，在长大区间列车的牵引过程包括起动牵引和途中运行牵引两部分。列车起动牵引的能耗，等于列车用能效率特征值在速度0～v1范围内的平均值与速度v1的乘积。列车途中1次“牵引—惰行”的能耗，等于列车用能效率特征值在速度v2～v1范围内的平均值乘以速度v2与v1之差。因此，长大区间的列车用能效率特征值的平均值可表示为

(14)

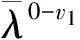
4　算例分析

4.1　列车属性影响牵引能耗灵敏度的算例分析

以城市列车运行计算系统[3,9]为基础，仿真某列车Tr1运行于区间AB，进行列车属性的灵敏度分析。列车Tr1的参数见表1，区间AB的线路条件见表2。列车采用“牵引—惰行—制动”的策略运行，限速v1为80 km·h-1，制动开始速度v2为60 km·h-1。列车运行的牵引能耗为25.3 kW·h。

以列车Tr1的参数和AB区间的线路参数为参照，分别改变列车质量、单位基本阻力和牵引电机效率，得到的牵引能耗变化率仿真结果见表3。

由表3可知，列车质量变化导致的牵引能耗变化率大于列车质量变化率；单位基本阻力变化导致的牵引能耗变化率小于单位基本阻力的变化率；牵引电机效率下降导致的牵引能耗上升比率大于牵引电机效率下降的比率，而牵引电机效率提高导致的牵引能耗下降比率小于牵引电机效率提高的比率。显然，列车质量对牵引能耗的影响程度大于单位基本阻力，而牵引电机效率对牵引能耗的影响程度随牵引电机效率的提高而减小。该结果与上文用灵敏度分析方法得到的结论一致。

表1　列车Tr1参数

表2　区间AB线路条件

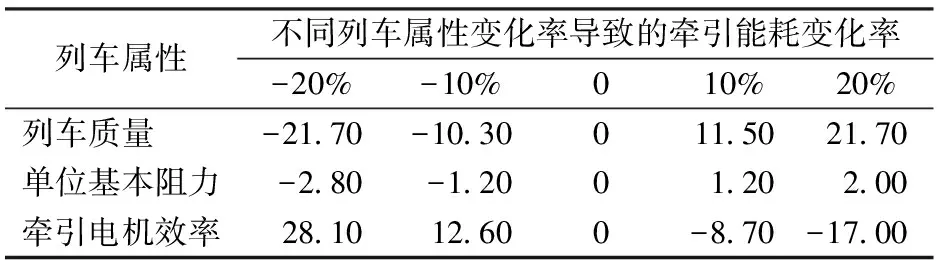
表3　不同列车属性变化下的牵引能耗变化率　%

因此，从节能角度考虑，车体轻量化设计最有利于降低牵引能耗，节能效果会比较明显；而城市轨道交通列车的速度较低，列车运行过程所受到的阻力相对较小，对列车的流线设计要求不必太高。在牵引电机效率较低时，改善牵引电机效率将显著节约牵引能耗，而牵引电机效率已经较高时，再提高牵引电机的效率，得到的节能效果则不再明显。

4.2　列车用能效率的算例分析

以Tr1—Tr6这6列列车为研究对象，对各列车的用能效率进行分析。列车均为B型车。除Tr5, Tr6编组为4动2拖外，其余列车编组为3动3拖。各列车质量、单位基本阻力、牵引力及牵引电流见表4。

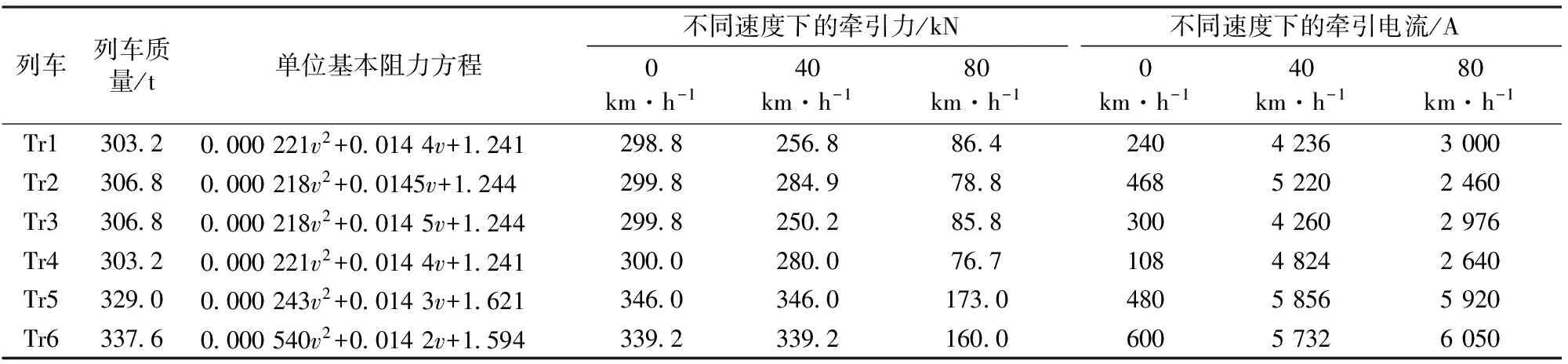
表4　列车参数

由表4可知，Tr1, Tr4的列车质量与单位基本阻力一样，但牵引力和牵引电流各不相同；Tr2, Tr3的列车质量稍重，单位基本阻力、牵引力和牵引电流均稍有不同；Tr5, Tr6的列车质量最重，牵引电流最大，其牵引力也最大。可见，各列车的用能效率难以通过某一列车属性判断。

根据列车参数计算不同列车用能效率特征值随列车速度变化的情况如图3所示。

图3　不同列车用能效率特征值随速度的变化

由图3可知，由于Tr5, Tr6的列车用能效率特征值在各个速度下均处于较高水平，因此这2列列车的用能效率较低；而Tr4的列车用能效率特征值在各个速度下均比较小，故其用能效率较高；Tr1的列车用能效率特征值在低速下都较低，但在60 km·h-1之后迅速增长，因此，该列车在低速下运行比较节能，适合运行于受站间距限制、列车速度较低的市中心线路；相反，Tr2的列车用能效率特征值在低速下较高，而在60 km·h-1之后较低，适合运行于站间距较大、列车速度较快的通勤线路。

列车在区间上的用能效率由列车用能效率特征值的平均值反映。假设限速v1为80 km·h-1，惰行速度v2为60 km·h-1，计算得到不同牵引次数时列车用能效率特征值的平均值，结果见表5。为简便计算，表中的列车用能效率特征值在速度区间内的平均值由各速度下的算术平均值代替。

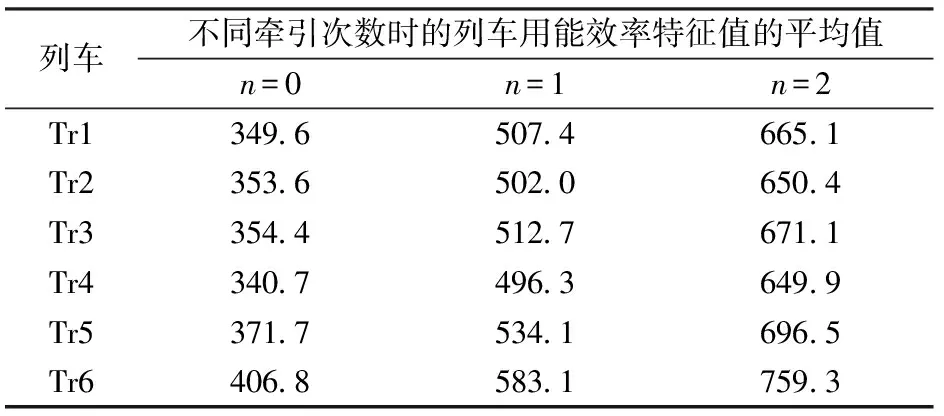
表5　列车用能效率特征值的平均值　W·h2·km-1

由表5可知， 牵引次数n=0时列车用能效率特征值的平均值大小序列为Tr6>Tr5>Tr3>Tr2>Tr1>Tr4，由此可以推断，在短站间距的线路上，Tr5与Tr6的列车用能效率较低，Tr4的较高；n=1, 2时的列车用能效率特征值平均值大小序列为Tr6>Tr5>Tr3>Tr1>Tr2>Tr4，因此，在长站间距的线路上，Tr5与Tr6的列车用能效率比较低，Tr3的较它们略低，Tr4的处于较高水平。

采用城市列车运行计算系统[9]，对各列车在同一线路上采用相同操纵模式仿真运行时的牵引能耗进行比较，以验证列车用能效率特征值的有效性。上述6列列车分别以节能操纵模式[3]仿真运行于4条实际线路，线路条件见表6。表中，S1与L1实为同一线路，但列车在L1线路运行时隔站停车，停站次数较在S1线路运行时减少一半。

表6　线路条件

各列车在这4条线路上的牵引能耗情况如图4所示。

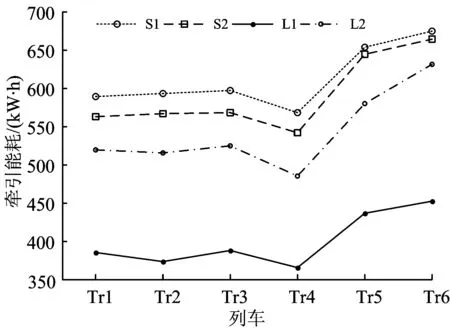
图4　各列车在不同线路上的牵引能耗

由图4可知，在4条线路上，列车Tr5, Tr6的牵引能耗始终处于较高水平，列车Tr4的则较低，而列车Tr1, Tr2, Tr3的比较接近；Tr1与Tr2在长站间距与短站间距线路上的牵引能耗情况有所不同，在短站间距线路S1, S2上运行时Tr2的牵引能耗高于Tr1，而在长站间距线路L1, L2上运行时反之。

仿真能耗结果及列车用能效率的评估结果对比见表7。

表7　牵引能耗与列车用能效率对比

由表7可知，在短站间距与长站间距线路上得到的各列车用能效率和牵引能耗大小序列与以表5列车用能效率特征值的平均值分析得出的仿真结果完全一致；同时，列车用能效率特征值相近的列车，其牵引能耗也相近；因此，可以认为列车用能效率特征值可以准确判别不同列车的用能效率。

对比列车在线路S1和L1上运行的牵引能耗可知，由于停站次数减少，列车在L1上运行的牵引能耗更小。其中，列车Tr2的牵引能耗下降最多，表明其更适合于长站间距的线路；而列车Tr1的牵引能耗下降最少，可反映出其更适合于短站间距的线路。这与对图3列车用能效率特征值的分析结果也一致。这表明，根据列车用能效率特征值随列车速度变化的规律可以分析各列车在不同类型线路上节能运行的适用性。

5　结　论

(1) 基于列车牵引能耗模型，分析得出影响牵引能耗的列车属性主要有列车质量、单位基本阻力、牵引力及牵引电流。其中，牵引电机效率决定了列车牵引力和牵引电流。

(2) 通过对各列车属性的灵敏度分析与算例验证，得出：列车质量导致的牵引能耗变化幅度大于列车质量变化的幅度；单位基本阻力变化导致的牵引能耗变化幅度小于单位基本阻力变化的幅度；牵引电机效率下降导致牵引能耗上升的幅度大于牵引电机效率下降的幅度，而牵引电机效率提高导致的牵引能耗下降幅度小于牵引电机效率提高的幅度。列车质量对牵引能耗的影响最大，单位基本阻力对牵引能耗的影响最小，牵引电机效率对牵引能耗的影响程度随牵引电机效率的提高而减小。

(3) 定义牵引能耗模型中的被积函数为列车用能效率特征值，用以评价列车的用能效率。仿真表明，各列车的用能效率特征值排序与其在相同线路仿真运行时的牵引能耗一致。因此，列车用能效率特征值可以准确判别不同列车的用能效率。

(4) 列车用能效率特征值是随列车速度上升而上升的变量，其随速度变化的规律可用于分析不同列车在不同类型线路上节能运行的适用性。在限速80 km·h-1的线路上，低速(0～60 km·h-1)运行时列车用能效率特征值的上升幅度较小、或高速(60～80 km·h-1)运行时上升幅度较大的列车适于在短站间距线路上节能运行；反之，则适于长站间距线路上节能运行。

(5)本文在分析列车属性对牵引能耗的影响时未考虑再生制动。不同列车的制动电流特性曲线有所不同，其对牵引能耗的影响将在今后进行研究。

[1]孔令洋,梁青槐,张岩,等.直线电机轮轨交通系统牵引能耗研究[J].铁道学报, 2007, 29(6): 106-112.

(KONG Lingyang, LIANG Qinghuai, ZHANG Yan, et al. Study on Traction Energy Consumption of Linear Induction Motor Rail Transit System[J]. Journal of the China Railway Society, 2007, 29(6): 106-112. in Chinese)

[2]HOYT E V, LEVARY R R. Assessing the Effects of Several Variables on Freight Train Fuel Consumption and Performance Using a Train Performance Simulator[J]. Transportation Research Part A: General, 1990, 24(2): 99-112.

[3]刘海东,毛保华,丁勇，等.城市轨道交通列车节能问题及方案研究[J].交通运输系统工程与信息, 2007, 7(5): 68-73.

(LIU Haidong, MAO Baohua, DING Yong, et al. Train Energy-Saving Scheme with Evaluation in Urban Mass Transit Systems[J]. Journal of Transportation Systems Engineering and Information Technology, 2007, 7(5): 68-73. in Chinese)

[4]IFEU (Institute for Energy and Environmental Research Heidelberg). Energy Savings by Light-Weighting[R]. Heidelberg: International Aluminium Institute, 2003.

[5]RAGHUNATHAN R S, KIM H D, SETOGUCHI T. Aerodynamics of High-Speed Railway Train[J]. Progress in Aerospace Sciences, 2002, 38(6): 469-514.

[6]DOMINGUEZ M, CARDADOR A F, CUCALA A P, et al. Energy Savings in Metropolitan Railway Substations through Regenerative Energy Recovery and Optimal Design of ATO Speed Profiles[J]. IEEE Transactions on Automation Science and Engineering, 2012, 9(3)：406-504.

[7]荀径,唐涛,宋晓美,等.再生制动条件下的城轨列车节能驾驶综合模型[J].中国铁道科学, 2015, 36(1): 104-110.

(XUN Jing, TANG Tao, SONG Xiaomei, et al. Comprehensive Model for Energy-Saving Train Operation of Urban Mass Transit under Regenerative Brake[J]. China Railway Science, 2015, 36(1): 104-110. in Chinese)

[8]LIU R, GOLOVITCHER I M. Energy-Efficient Operation of Rail Vehicles[J]. Transportation Research Part A, 2003, 37(10): 917-932.

[9]毛保华,何天键,袁振洲,等.通用列车运行模拟软件系统研究[J].铁道学报, 2000, 22(1): 1-6.

(MAO Baohua, HE Tianjian, YUAN Zhenzhou, et al. A General-Purposed Simulation System on Train Movement[J]. Journal of the China Railway Society, 2000, 22(1):1-6. in Chinese)