基于混成自动机的城市轨道交通ZC子系统建模与验证方法
黄友能,张鹏基,侯晓鹏,唐 涛
(1.北京交通大学 电子信息工程学院,北京 100044;2.北京交通大学 轨道交通运行控制系统国家工程研究中心,北京 100044)
基于通信的列车控制系统(Communication Based Train Control,CBTC)是保证城市轨道交通列车安全、高效运行的系统,其区域控制器(Zone Controller,ZC)子系统主要实现为管辖范围内列车计算移动授权(Movement Authority,MA)、区域控制器边界切换等功能[1],这些功能的安全性是保障行车安全的基础,因此针对ZC子系统功能的安全验证就显得尤为重要。
ZC子系统主要通过无线传输方式接收车载子系(Vital OnBoard Computer,VOBC)的信息,因此在车地通信过程中不可避免会出现信号延迟或发送失败等情况,同时,由于ZC子系统在同一时间段内会与管辖范围内的所有列车进行交互,因此要求该系统应具有较强的并发性与实时性。另外,ZC子系统在计算移动授权的过程中,需要考虑列车连续变化参数(距离、速度和加速度等)的演化过程,以及设备交互的一些离散事件,具有明显的混成特性[2]。
关于列车控制系统安全验证的既有研究工作,有的针对系统的并发性与实时性进行建模与验证,如同济大学的徐中伟教授等利用Petri网模型和故障树实现了对联锁软件的安全性评估等[3],但缺少相应的验证环节。有的针对系统混成特性进行研究,如北京交通大学的吕继东博士利用混合通信进程对系统进行建模仿真,但缺少相应的验证软件[4]。北京交通大学的刘金涛博士利用动态微分逻辑形式化语言对CTCS-3级列车控制系统进行了仿真与验证,但验证过程需要大量的推导公式,效率和重用性都较低。
本文基于形式化建模验证理论[5-6],结合统一建模语言(Unified Modelling Language,UML)的交互流程描述能力和自定义扩展能力,针对ZC子系统的混成特性,建立ZC子系统的UML顺序图;采用模型转换方法,定义从源模型到目标模型的转换规则,将ZC子系统的UML顺序图转换为线性混成自动机模型,用于ZC子系统功能的安全验证;以实际的ZC子系统边界切换控制功能场景为例,根据建立的ZC子系统线性混成自动机模型,采用形式化工具BACH(Bounded reachability checker)对该场景的7条功能性质和4条安全性质进行验证。
1 功能场景建模方法
针对ZC子系统具有连续变量(距离、速度和加速度等)的动态特性,首先采用UML顺序图描述系统的实时交互特性,然后利用UML的标记值和约束的扩展方式对顺序图进行扩展,给出模型转换的定义及规则,使源模型与目标模型的语义相同,将顺序图转换为线性混成自动机模型。
1.1 UML顺序图扩展
为了能够表达ZC子系统的混成特性,需要对UML顺序图进行扩展[7]。将顺序图中的消息发送和消息接收采用事件表示,利用标记值和约束的扩展方式,对顺序图进行了以下2个方面的扩展。
1)对时间的扩展
(1)事件上添加时钟及其约束(可有多个时钟),即本事件在什么时间范围内发生;
(2)事件上添加时钟变化率恒为1(以1 ms为时间单位长度);
(3)动作的时间约束,即只有满足时间约束时动作才会发生;
(4)动作的时钟重置,即动作完成时要进行时钟重置。
2)对连续变量的扩展
(1)事件上添加变量的约束(可有多个变量),即本事件发生时变量的变化范围;
(2)事件上添加变量的变化率(可为实数范围如[0.9,1.1]);
(3)动作的变量约束,即只有满足变量约束时动作才会发生;
(4)动作的变量赋值,即动作完成时要进行的变量赋值。


图1 UML扩展内容展示
1.2 线性混成自动机定义
以Alur提出的定义框架为基准[8],对线性混成自动机作如下定义。
定义1
线性混成自动机(Linear Hybrid Automata)形式为
H:(X,Y,V,E,V0,fflow,iinv,iinit)
其中各个参数的含义如下。
X:实数值系统变量的有限集合,X={x1,x2,…,xn},其中n为变量的个数,也被称为自动机的维度(dimension)。
Y:动作名有限集合。
V:位置节点的有限集合。
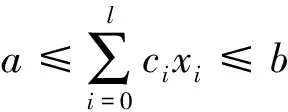
V0:初始位置节点集合。

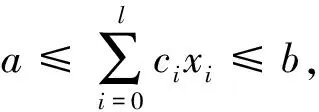

1.3 模型转换的定义、规则和步骤
1.3.1模型转换的定义
UML顺序图定义了多种类型的交互片段,这些交互片段组成了UML顺序图的不同生命线即对象间的活动。本文在此基础上增加定义了单元片段,用于刻画比较简单的消息传递过程。按照该定义,交互片段也可看作是由众多单元片段按照一定规则组合而成的。
定义1:
单元片段语义表示为1个或多个可视的事件序列,每个单元片段由相应的单个或多个事件序列组成。事件e1和e2间的关系应当满足以下3种关系之一。
(1)在初始事件中,e1为消息发送事件,则e2为相对应的消息接收事件。
(2)若在同一实例的生命线上,事件e1出现在e2之前,则e1是消息发送事件;并且事件e1和e2可作为可视对(e1,e2)。
(3)若在同一实例的生命线上,事件e1出现在事件e2之后,则e2是消息发送事件。
定义2:
1个单元片段是1个8元数据组,可表示为UF(I,W,M,Z,B,C,G,J)。
其中各参数的含义如下。
I:对象的有限集合。
W:事件的有限集合,W*为包括空事件串在内的所有不重复事件串集合,p为事件串集合,∀p∈H*,|p|为p的字符个数,p(n)为p中的第n个事件,2个事件用“.”连接。
M:有穷的动作集合,包括消息的接收与发送。
Z:可视对事件集合,Z={e,e′}代表1个可视对。
B:事件约束集合(包括时间与变量)。
C:事件间约束集合(包括时间与变量)。
G:事件标签值集合(时间与变量的变化率)。
J:消息赋值集合。
1.3.2模型转换的规则
1)单元片段转换规则
将单元片段进行转换,得到目标单元自动机A(N,n0,L)。
UF(I,W,M,Z,B,C,G,J)→A(N,n0,L)
其中各参数的含义如下。
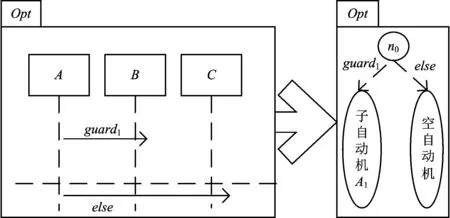
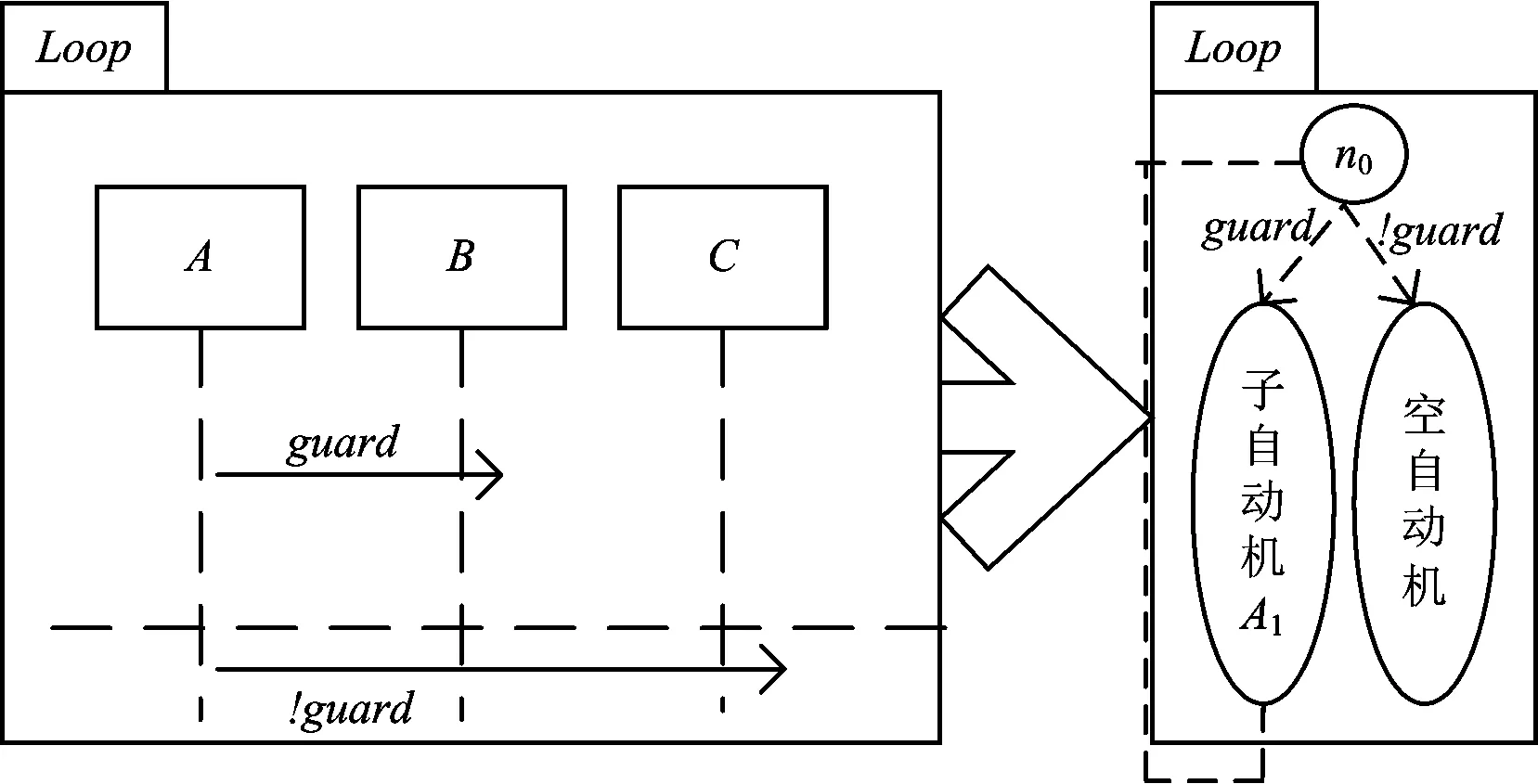
N:节点集合,N={p,d,r},其中,p∈W*,并且对于∶∀j n0:集合N的1个空状态。在每个单元片段上都建立1个空状态,以便后期的组合优化。 L:目标单元自动机事件集合,L={l′,g,m,a,l},与混成自动机转换关系集合E相对应,其中l′和l为自动机的2个节点对应于UML中可视事件对,且l′,l∈N;g为迁移条件,即进行状态跳变时变量需要满足的条件,是UML图中接收发送消息需要满足的时间或变量条件的扩展;m为动作集合,对应于UML图中消息的发送与接收;a为动作过程中赋值更新的集合,对应于UML图中动作的时间重置与变量赋值更新扩展。 2)组合片段转换规则 规则1:在1个多分支交互片段“Alt”中有q个互斥的可选分支,每个分支上都有执行该分支的“使能”条件,只有条件为真的分支才被执行,每个分支是1个单元片段或者组合片段。 定义函数Alt(g,AF), 其中g为对应可选分支的门条件,AF为所有可选片段的集合, 则可按照以下规则得到自动机AAlt(N,n0,L)。 Alt(g,AF)→AAlt(N,n0,L) 其中 N={n0}∪N1∪N2… L={〈n0,ε,guard1,ε,n1,0〉,〈n0,ε,guard2,ε,n2,0〉}…∪L1∪L2… 式中:N1和N2为节点集合N的子集合;guard1和guard2为所要满足条件集合guard中的子条件;n1,0和n2,0为集合N的另外2个空状态;L1和L2为有限集合L的子集合。 图2为有2种选择的Alt组合片段转换规则示意图,图中A,B,C为组合片段的组合对象;A1和A2为子自动机。 图2 组合片段Alt转换规则示意图 规则2: 1个组合片段Opt是1种单选择行为,这种单选择行为类似于Alt组合片段中的某种行为。 定义选择片段函数Opt(OF),其中OF为单分支选择片段变量,可按照以下规则得到自动机AOpt(N,n0,L)。 Opt(OF)→AOpt(N,n0,L) 其中 L={〈n0,ε,guard1,ε,n1,0〉,〈n0,ε,else,ε, n2,0〉}∪L1∪L2 式中:else为除guard外需要满足的其他条件。 图3为1个组合片段Opt的转换规则示意图。 图3 组合片段Opt转换规则示意图 规则3:1个组合片段Loop表示1种循环行为,组合片段中的子片段会被不断重复直到不满足条件为止。 设函数Loop(LF,guard), 其中LF为所要不断重复的子片段,guard为所要满足的条件, 则可按照以下规则得到自动机ALoop(N,n0,L)。 Loop(LF,guard)→ALoop(N,n0,L) 其中 N={n0,ne}∪N1 L={〈n0,ε,guard,ε,n1,0〉,〈n0,ε,!guard,ε,ne〉}∪L1 式中:ne为集合N的1个新的空状态;e为自然数。 图4是1个组合片段loop转化规则示意图,图中A1为需要循环片段构造的子自动机。 图4 组合片段Loop转换规则示意图 规则4:多个组合片段可组成1个完整的自动机,组合片段按照生命线由上到下的顺序执行。 设函数Combin(CF), 其中CF为所有的组合片段,guard为所要满足的条件,则可按照以下规则得到自动机ACombin(N,n0,L)。 Combin(CF)→ACombin(N,n0,L) 其中, N=N1∪N2… n0=n1,0 L={〈ni,e,ε,ε,ε,ni+1,0〉}∪L1∪L2 (1≤i≤m-1) 式中:ni,e为集合N的另外的空状态,i和e均为自然数。 1.3.3模型转换的步骤 在得到1个扩展的UML顺序图之后,经过以下4步将其转换为目标线性混成自动机。 Step1:将扩展后的UML顺序图根据时间先后顺序拆分为不同组合片段,由于组合片段内可能会嵌套着其他组合片段和单元片段,需要将组合片段继续拆分,直至将整个顺序图拆分为单元片段。 Step2:根据单元片段转换规则,将单元片段转换为目标单元自动机。 Step3:根据组合片段转换规则,将1个组合片段对应的多个单元片段都转换成目标单元自动机,然后再组合成该组合片段对应的线性混成自动机。 Step4:根据拆分组合片段时的顺序,将不同组合片段的线性混成自动机合成为完整的目标线性混成自动机模型。 针对CBTC系统的混成特性,根据北京地铁亦庄线ZC边界切换工程数据选取列车在小红门ZC与亦庄桥ZC边界切换控制功能场景进行具体建模与验证。ZC通信周期为400ms,VOBC通信周期为200 ms。 当列车从1个ZC管辖区域进入另一个ZC管辖区域时,ZC将根据移交ZC发送的移动MA判断列车是否已经运行到地面区域分界点,如果已经到达地面区域分界点,则由移交ZC向接管ZC发出移交列车申请,此后由这2个ZC分别计算列车在各自管辖范围内的MA,并由当前控制列车ZC负责将这2部分MA信息混合后发送给列车。在车地通信正常的情况下,列车将接收到MA,并根据移动授权计算速度曲线;如列车在5 s内仍接收不到新的MA,将认为在ZC切换过程中发生了车地通信故障,列车将触发紧急制动,使列车在车地通信故障前接收到的移动授权终点前停车。 列车从小红门ZC管辖区域进入亦庄桥ZC管辖区域时,越区切换的具体过程可以分为以下5个阶段。 阶段1:如图5所示,列车在小红门ZC区域内运行,当MA终点为小红门ZC区域与亦庄桥ZC区域边界点JZ9时,此时小红门ZC(移交ZC)将与亦庄桥ZC(接管ZC)通信,触发边界切换控制功能。 图5 ZC边界切换触发控制图 阶段2:在车地通信正常的情况下,如图6所示,随着列车的运行,移交ZC为列车计算移动授权MA1,接管ZC为列车计算移动授权MA2,由于此时列车仍受到移交ZC控制,移交ZC将MA1和MA2的信息混合后向列车发送“终点至H点”的移动授权。 图6 车地通信正常情况下ZC边界切换控制图 阶段3:当列车车头位置越过ZC边界JZ9时,此时移交ZC为列车计算移动授权MA1,接管ZC为列车计算移动授权MA2,列车受接管ZC的控制,由接管ZC将MA1和MA2的信息混合后向列车发送“终点至H点”的移动授权。 阶段4:在列车车尾越过ZC边界JZ9时,将向移交ZC发送注销申请,并根据接管ZC发送的移动授权完成行车作业。假如列车车尾在越过ZC边界JZ9时前方有障碍物等情况,则计算安全制动曲线并根据曲线完成停车过程。 阶段5:在车地通信故障的情况下,如图7所示,列车将触发紧急制动,列车在H点前停车。 图7 车地通信故障情况下ZC边界切换控制图 首先定义参数,见表1。 表1 参数定义表 针对ZC边界切换控制功能场景,采用扩展的UML顺序图,建立ZC边界切换控制功能场景的UML顺序图;根据车地通信的5个阶段,将建立的UML顺序图分为5个组合片段;以其中1个组合片段1为例,其UML顺序图如图8所示。 根据模型转换的定义和规则,将图8所示的UML顺序图转换为单元自动机;将所有的单元自动机根据转换的先后顺序组合成线性混成自动机模型,如图9所示。 本文利用线性混成自动机的形式化验证软件BACH对该场景的功能性质和安全性质进行验证。BACH是南京大学设计开发的面向线性混成系统有界可达性的模型验证软件,它将BMC思想扩展到了线性混成自动机的可达性检验工作中。该工具主要检验功能有:单元自动机面向路径可达性验证;单自动机有界可达性验证;自动机组系统面向路径组可达性验证;自动机组系统有界可达性验证。本文主要运用后2种验证功能。 根据图9所示的ZC边界切换控制功能线性混成自动机模型,采用BACH模型验证软件提供的可以针对每个成员自动机分别建立模型的功能,分别建立该具体场景下VOBC,移交ZC和接管ZC的线性混成自动机模型,如图10所示。 图8 ZC边界切换控制功能场景部分UML顺序图 图9 ZC边界切换控制功能场景线性混成自动机模型 图10 VOBC,移交ZC和接管ZC的线性混成自动机模型 通过BACH软件中检测模块CLHA Checker对场景模型进行功能性验证。利用检测模块CLHA Checker中的Path-Oriented Reachability选项先对模型中自动机组的路径可达性进行检测,然后针对ZC子系统边界切换场景的7条功能性质进行验证。检测路径及验证结果如表2所示。 利用检测模块CLHA Checker中的Bounded Reachability选项对自动机组的有界可达性进行检测。在有界可达性的检测过程中加入各个对象的线性混成自动机编码文本。为了验证列车安全性能,在VOBC线性混成自动机模型中加入减速状态和超速状态,选择终点目标节点,然后根据目标节点选择待可达性的检查节点进行有界可达性检测。检测完成后再针对4条安全性质进行验证,安全性质及验证结果见表3。 表2 功能性质验证 表3 安全性质验证 在考虑了ZC边界切换控制中车地通信正常以及故障2种情况的基础上,通过表2中的7条路径可达性性质验证可以看出,ZC边界切换控制功能符合设计要求;通过表3中4条有界可达性安全性质验证可以看出,在ZC边界切换控制功能场景下,列车能够安全通过地面区域边界点,也没有超速情况,且能够在接管ZC管辖范围内安全停车。但由于本案例在设计之初将障碍物的位置设置的距离边界点较近,使得在ZC切换过程中,列车尚未完全通过边界点就开始降速停车了。在将障碍物位置后移之后,通过检测发现减速状态可达,说明列车能够安全通过地面区域边界点且无降速,符合安全需求。 本文针对ZC子系统具有混成性的特点,利用扩展后的UML顺序图对ZC子系统进行建模;采用模型转换方法,定义从源模型到目标模型的转换规则,将ZC子系统的UML顺序图模型转换为形式化的线性混成自动机模型,用于ZC子系统功能的安全验证。以北京地铁亦庄线ZC边界切换控制功能场景为例,建立该场景的UML顺序图;将其对应车地通信的5个阶段细分为5个组合片段;根据模型转换定义及规则,进一步将各组合片段拆分为单元片段,将1个组合片段对应的多个单元片段转换成目标单元自动机后,再合成该组合片段对应的线性混成自动机;根据拆分组合片段时的顺序,将不同组合片段的线性混成自动机合成为完整的目标线性混成自动机模型。根据建立的线性混成自动机模型,采用验证工具BACH对该场景的7条功能性质和4条安全性质进行验证。结果表明:ZC边界切换控制功能满足设计要求,列车能够安全通过地面区域边界点,没有超速情况且能够在接管ZC管辖范围内安全停车。表明所提出的建模和验证方法是可行的,弥补了对具有混成特性列车控制系统既有验证方法的不足。 [1]唐涛,郜春海,黄友能,等. CJ/T 407—2012 城市轨道交通基于通信的列车自动控制系统技术要求[S].北京:中国标准出版社,2012. (TANG Tao,GAO Chunhai, HUANG Youneng,et al. CJ/T 407—2012 Technical Requirement of Communication Based Automatic Train Control System for Urban Rail Transit[S].Beijing:China Standard Press,2012.in Chinese) [2]刘金涛,唐涛,赵林,等. 基于微分动态逻辑的无线闭塞中心交接协议建模与验证[J].中国铁道科学,2012,33(5):98-104. (LIU Jintao,TANG Tao,ZHAO Lin,et al. Modeling and Verification of Radio Block Center Handover Protocol Based on Differential Dynamic Logic[J]. China Railway Science,2012,33(5):98-104.in Chinese) [3]杜军威, 徐中伟, 王树梅. 联锁逻辑模型的安全性分析[J].计算机工程与应用,2007,43(2):1-4. (DU Junwei, XU Zhongwei,WANG Shumei. Safety Analysis of Interlocking Logic Model[J]. Computer Engineering and Applications, 2007,43(2):1-4.in Chinese) [4]吕继东. 列车运行控制系统分层形式化建模与验证分析[D]. 北京:北京交通大学, 2011. (LÜ Jidong, Hierarchical Formal Modeling and Verification Train Control System[D].Beijing:Beijing Jiaotong University,2011.in Chinese) [5]PLATZER A′e,QUESEL Jan-David. European Train Control System: a Case Study in Formal Verification[J]. Lecture Notes in Computer Science,2009,5885:246-265. [6]WERNER Damm, ALFRED Mikschl, JENS Oehlerking, et al. Automating Verification of Cooperation, Control and Design in Traffic Applications[J]. Lecture Notes in Computer Science,2007,4770:115-169. [7]ONJECT Management Group. Unified Modeling Language:Super Structure[EB/OL].2013-07-30[2015-04-15]. http://www.omg.org. [8]ALURA R,COURCOUBETIS C,HALBWACHS N,et al.The Algorithmic Analysis of Hybrid Systems[J]. Theoretical Computer Science, 1995, 138(94):3-34.
2 ZC子系统建模与验证案例
2.1 ZC边界切换控制功能场景分析


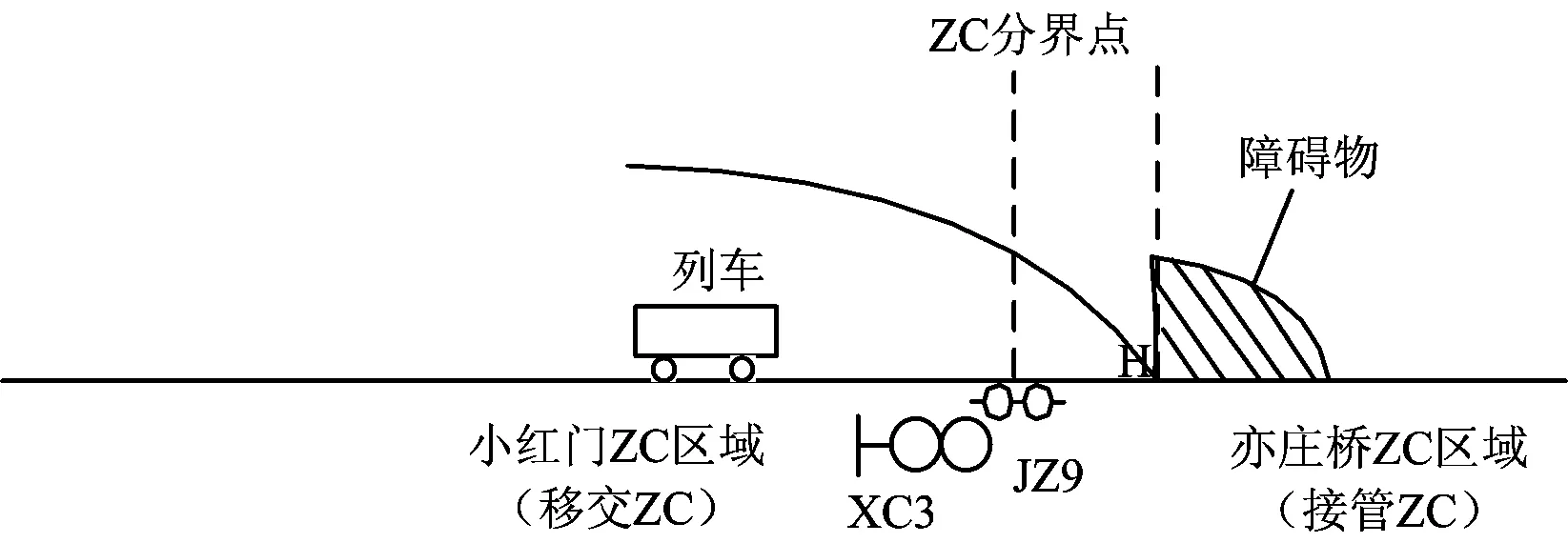
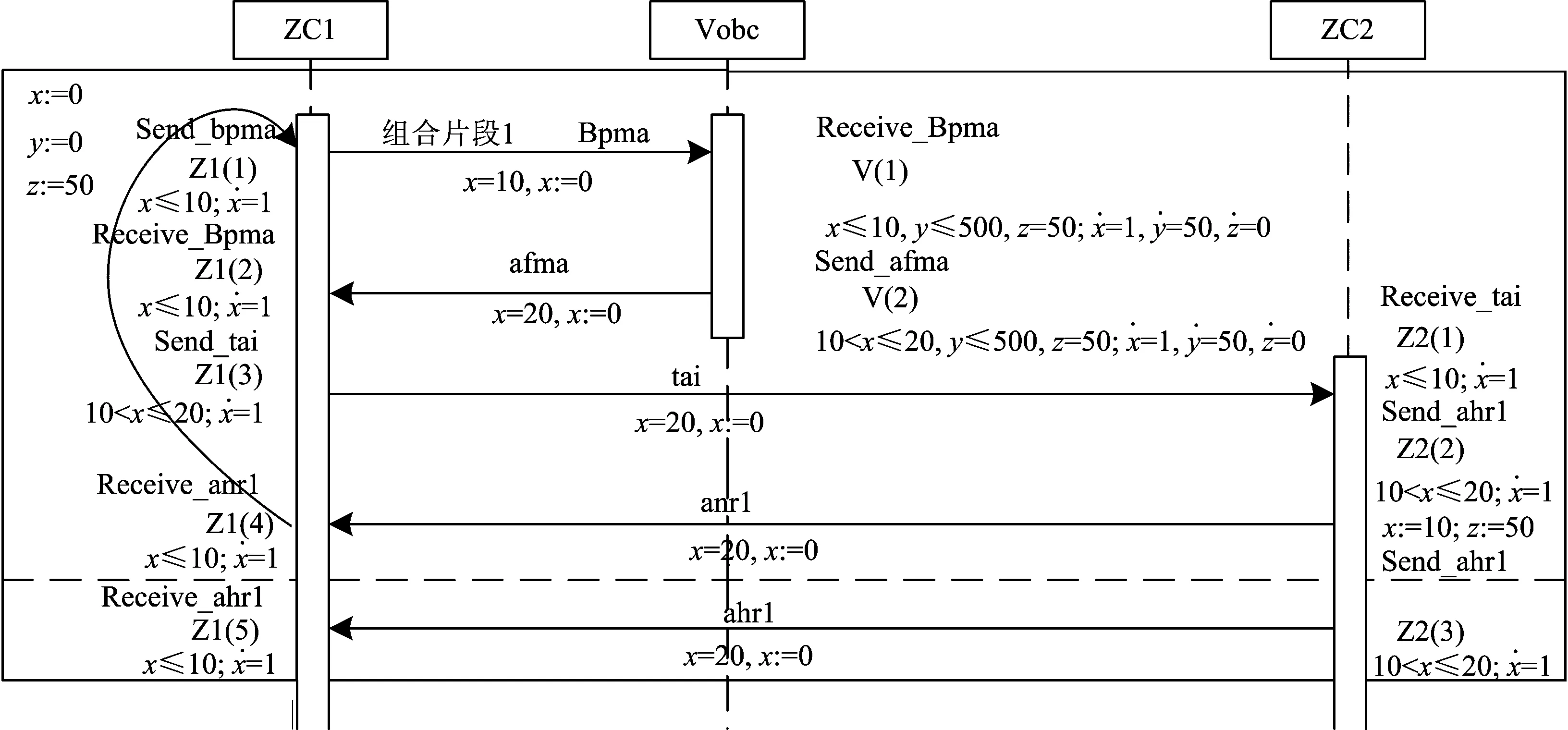
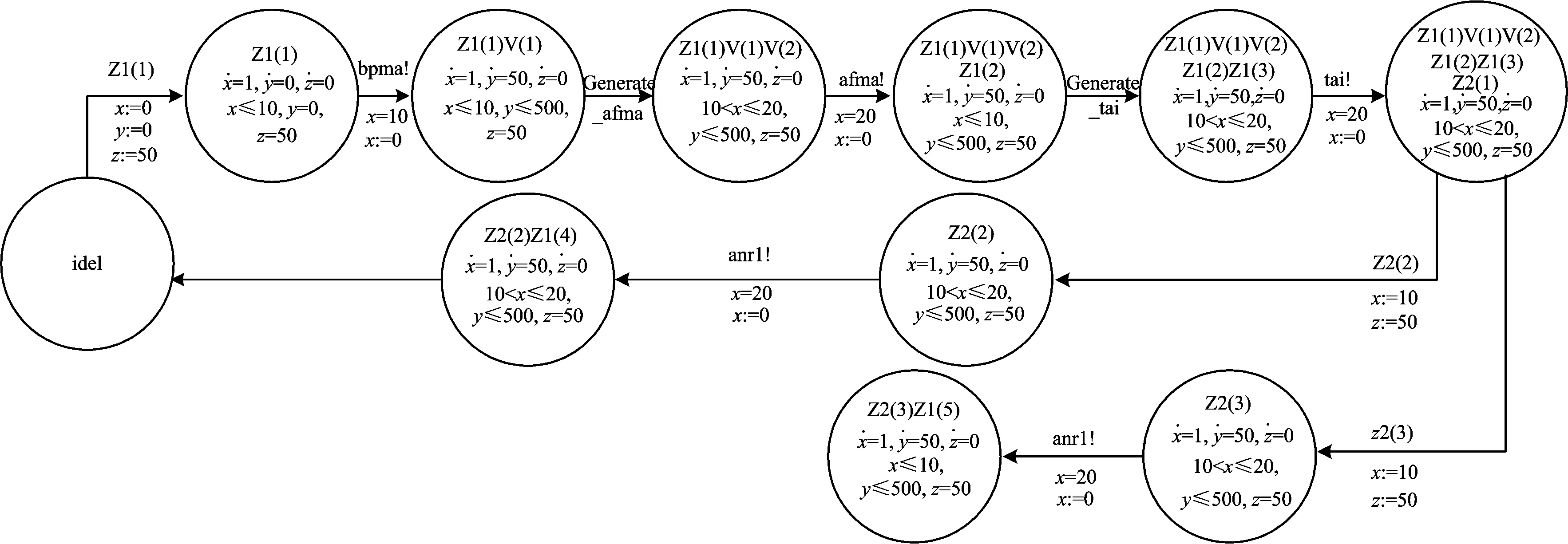
2.2 ZC边界切换控制功能场景建模

2.3 验证及结果分析





3 结 论

