沟通算法,让笔算除法更精彩
石柳
[摘 要]学生在学习“除数是一位数的除法”时,已经掌握了笔算除法的基本方法,而“除数是两位数的除法”的计算原理与“除数是一位数的除法”相同,只是试商的难度加大。为解决这一问题,教学“除数是两位数的除法(例2)”一课时,可以典型错题为载体,通过进一步的剖析错因、分析访谈,找准学生的知识起点,沟通计算方法间的联系,有效消除学生在试商时出现的错误。
[关键词]笔算除法 典型错题 应用 教学改进
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2016)08-023
人教版小学数学四年级上册第五单元安排了“除数是两位数的除法”这一内容,从以往的教学情况来看,学生在学习例2(除数接近整十数)时,掌握算理与试商过程的接受能力较弱,往往需要教师延长课时加以强化。笔者针对此问题,结合《小学数学一至六年级典型错题库》中的相关错例,重新思考并实践。
一、驻足——典型错题的再现与解读
典型错题1:笔算168÷18。
学生错解:

师:你这么快就商出了8!算完后检查了吗?
生1:检查了,8×18=144,我没算错,也没有减错。
师:可余数和除数有怎样的关系?
生1:余数不能比除数大。
师:看一看,发现了什么?
生1:哦,24比18大,商错了。
……
师:说说看,你是怎么算的?
生2:把18看成20,168÷20可以商8,就写8,再算8×18=144、168-144=24。
师:算得挺流利的,但其中有没有错误呢?
生2:我明白了,余数太大了,要商9。
……
错因剖析:
(1)学生层面。
因为是新授课,学生的关注点是“我怎样快速地找到商”,一般都以把除数看成最接近的整十数去试商这种方法解题,于是只要商的数字比较合理了,学生就会以为题目做对了;学生对两位数乘一位数的乘法口算不熟练,不能一下子算出准确答案跟被除数进行比较,对究竟是不是最合适的商判断不准;学生的数感较弱,对于特殊位置的数的数感不强。
(2)教师层面。
教师在新授课时只注重向学生讲清算理,对一些学困生和不够仔细的学生来说,调商就是一个难点,因为他们易忽略余数和除数之间的关系,从而导致初商过小却没有调整。
典型错题2:笔算170÷37。
学生错解:

师:检查一下,这道题有没有什么问题?(生1看了好几遍,没反应)我倒发现了一个地方有问题。(生1重新拿起笔算)
师(看到生1还是写了160后叫停):这160是谁和谁相乘的?
生1:4和40。
师:是算它们的乘积吗?(生1咬着笔头,不做声)这是估算的积,应该算4×37的积。(生1重新算)
……
师:说说看,你是怎么算的?
生2:把37看成40,估计可以商4。
师:160是怎么来的呢?
生2:4×40。
师:是这样的吗?这是估出来的积,能写吗?
生2:要写4×37的积。
……
错因剖析:
(1)学生层面。
学生根据试商步骤,按部就班地进行计算:先将除数进行估算,估成整十数,再来试商,用试得的商去乘原来的除数。其实,在这个过程中,学生对“除数估成的那个数到底起什么作用”“为什么不能和商去乘”等问题还是模棱两可。因为不能一次找到商,部分学生用学到的试商方法去尝试的时候,受除数是一位数和整十数的除法笔算的影响,认为已完成了这个商、乘、减的过程,导致列好的竖式出错。
(2)教师层面。
教师在例题教学时让学生自己先尝试解决,然后在学生讲解解题的方法时,没有讲清“为什么要试商”“怎么试商”等问题,造成一些学生只听懂了一半。
二、起航——教学改进前的思考
从典型错题的剖析中,我们不难看出,造成学生错误的关键在于两个方面。如下:
1.缺失学生学习起点的把握
对学生来讲,把除数看作整十数来试商是学习的难点,因为这个过程集中了估算、口算、数感等一系列的思维活动。而我们一线教师往往对计算教学的理解存在误区,认为只要教方法,学生会做即可。其实,事实并不是这样的。现在为什么会有那么多的学生讨厌计算,原因在于教师不能顺着学生的思维进行教学设计。因此,在教学“口算除法”和“除数是整十数的笔算除法”时,教师要有意识地观察学生的计算习惯,准确把握学生的学习起点。
2.缺失算法之间的沟通
由于教师对学生学习起点的把握有所缺失,认为学生只要把教材当中所呈现的列竖式的方法掌握即可,导致学生在笔算时只是按部就班地进行计算,完全不知道“为什么要商在这儿”“为什么要这样商”。所以,在改进教学时,教师要懂得放手,让学生大胆地想方法,引导他们把心中那最真实、最朴素的算法暴露出来,可以是估算,可以是口算,亦可以是想乘算除……在这整个算法沟通的过程中,实质上就是对算理的领悟。
三、扬帆——教学改进的实践
课前热身:算一算老师的QQ号码。
240÷60= 720÷80= 150÷29≈ 452÷90≈ 160÷20=
92÷30≈ 140÷70= 200÷40= 284÷69≈
师(揭题):今天,我们继续学习“除数是两位数的除法”。
1.情境导入
师:今天回诸暨了,顺便带了点绍兴特产给爸妈和亲戚们。
出示信息:一共买了21包梅干菜,共付168元。
预设问题a:在付钱时,老师脑子里蹦出了一个数学问题,猜一猜是什么?(每包梅干菜多少钱?)
预设问题b:请你想一想,每包梅干菜的价钱超过10元吗?(生谈想法)
预设问题c:每包梅干菜的价格超过5元吗?(生谈想法)
预设问题d:一包梅干菜到底要多少钱?
师:请把自己的想法、算法大胆地写出来,不管用什么方法,只要能够算出结果,让同学们看得明白就可以了。
……
2.算法探究与交流
(1)探究168÷21的算法。
(生思考方法,师选择性板书,生方法预设如下)
①估算法:160÷20=8,168÷21=8。
有些学生用整十数的除法估算出商,正好是168÷21的商。
②口算法:168÷21=8。
有些学生的口算能力较强,能观察数字的特点写出商。
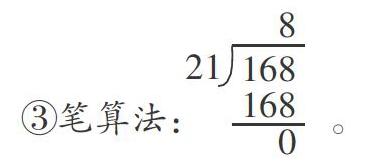
有些学生课前已有笔算经验,能够举一反三地写出竖式。
④做除法想乘法:21×8=168,168÷21=8。
有些学生的数感较强,能沟通乘除法间的联系。
(师根据学生的方法,让他们交流每一种方法所表示的意思)
……
师:168÷21为什么等于8?老师可以用画图法来进行验证。(通过数形结合呈现除法意义的原型)
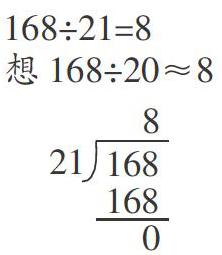
预设问题e:这么多种方法,你最欣赏哪一种?(让学生谈自己的想法)
师(小结):竖式是比较简洁的方法,它能够比较充分地体现计算的过程,而且它最神奇的地方就是把其他的方法都融合在里面了,不信请看!
师(边板书边概括,如右):168÷21,可以先把21估成20,想一想,168里面最多有几个20,就用8试商算21×8的乘积,正好是168,接着找到了正确的商。(板书时将学生采用的估算、口算、做除法想乘法等方法,融入列竖式的过程中)
……
(2)探究168÷28的算法。
师:梅干菜搞促销活动了,“买三送一”。
出示信息:买了21包梅干菜。
预设问题f:老板会送几包呢?(交流算法:21÷3=7)
出示:现在用168元钱买到了28包梅干菜,这时候每包梅干菜多少钱呢?
师:请把你的算法写下来,看谁写得又对又快。(由于有了对竖式的另一番理解,学生在写竖式时都有了自信)
(师在巡视中发现两种现象:一是许多学生先落笔商5,然后涂改成商6;另一种是先想了想,然后直接写6。师呈现学生计算中出现的这两种情况,揭示凃改前和想一想再写的原因)
师根据学生的讲解完善板书:

师(小结):从这题中我们发现,有时第一次试商会偏小,那么就要根据需要调一调商,改写成合适的商。
……
3.练习巩固
四、回望——教学改进后记
教学结束后,笔者出示84÷28、121÷17、324÷81、272÷68、243÷42五题笔算题,学生计算结果如下。
典型错题1的错误率降至4.35%,有两位学生计算121÷17出错,余数是19,商小了。
典型错题2的错误率降至0,没有再出现将估算的积写入竖式当中的现象。
然后笔者在当天并没有布置相应的家庭作业让学生进行巩固,而是在第二天对学生进行了跟踪分析。
在第二天的数学课上,笔者从配套练习中挑选了98÷31、294÷42、121÷29等算式进行测试,发现典型错题1的错解又出来了,所以可以断定,教材中呈现的在除数上面写整十数试商的方法会让学生在视觉上有错觉,无形当中误导学生用整十数去乘商。这种方法建议在之后的练习当中推荐,甚至可以不推荐,让学生把试商的过程放在大脑中完成,这样更有利于培养学生的试商能力。
尽管教材上有误导,但学生对于错误的纠正是很自觉的,不需要教师再重新点拨,这就缘于学生对竖式的理解,真正沟通了估算、口算、笔算等方法之间的联系。
综上可以看出,通过这样的教学改进,不仅有效消除学生计算中的典型错误,而且引导学生积极尝试新的学习方式,沟通了算法之间的内在联系,使得计算教学不再呆板,焕发出别样的精彩。
(责编 杜 华)

