基于区间直觉模糊TOPSIS法的节水灌溉工程方案优选
于倩雯,吴凤平,沈俊源
(河海大学商学院,江苏 南京 211100)
农业用水问题在我国水资源问题中一直占据着重要地位,作为世界第一人口大国,我国的农业用水效率与发达国家相比还处于较低水平。近几年,我国全国供水总量大约在5 500亿m3左右,农业灌溉用水量大约3 600亿m3,占全国总供水量的65%左右,是名副其实的用水大户。随着社会经济的发展及人民生活水平的提高,农业节水成为了缓解水资源短缺的根本之路。这不仅关系着我国的国计民生,同时也关系着我国粮食安全、水安全和生态安全的动态平衡,对于社会经济的可持续发展具有战略性的地位和作用。节水灌溉作为解决农业灌溉缺水问题和发展农业生产力的重要措施,能够转变农业传统的大水漫灌生产灌溉模式,最大限度的提高农业用水效率。节水灌溉工程方案的决策受到诸多因素影响,单因素或单目标的进行方案选择往往具有很大的片面性。从客观上来看,节水灌溉工程方案受到各个灌区自然气候条件、水文地貌、地方经济条件等因素的影响;从主观上来看,节水灌溉工程方案的选择也取决于国家及地方政府的政策导向、农作物种植结构、专业人才储备以及管理水平等因素。因此,如何对节水灌溉工程方案进行科学合理的决策,对于我国的用水安全以及产业经济的健康发展具有重要的现实意义。
目前,关于节水灌溉工程方案优选的研究已取得一定的成果。罗世良等[1]将投影寻踪模型应用到节水灌溉方案决策中去,根据投影值大小判断工程方案的优劣;郭法强等[2]考虑节水灌溉工程多属性、多指标的特点,建立了基于逼近理想点法的方案优选模型;高军省[3]从集对分析理论出发,根据欧氏距离计算节水灌溉方案评价的联系度,通过比较不同方案的联系度大小作出节水灌溉方案的优选决策;郭文献等[4]在模糊物元分析的基础上,提出了变异系数权重确定方法,建立了节水灌溉方案优选模糊物元分析模型;刘森等[5]阐述了模糊聚类方法在节水灌溉工程方案优选中的运用,并通过实例说明该模型的重要性。这些模型方法的提出对于节水灌溉方案的决策起到了积极促进作用,但是在实际运用过程中仍然存在综合优化指标不明确、权重确定主观偏差过大等问题。考虑到节水灌溉工程方案的决策因素众多,且决策信息容易受到主观因素影响,本文在前人研究的基础上建立了基于区间直觉模糊TOPSIS法的节水灌溉方案优选模型,结合信息熵原理改进权重确定方法,提出了区间直觉模糊熵权,并对各节水灌溉工程方案与正、负理想方案的相对接近程度进行优化排序从而达到方案优选的目的。
1 区间直觉模糊原理
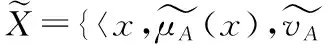
(1)
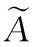
[1-μ+A(x)-v+A(x),1-μ-A(x)-v-A(x)]
(2)
定义2[8]:设α=([μ-ij,μ+ij],[v-ij,v+ij])是一个区间直觉模糊数,其中[μ-ij,μ+ij]⊂[0,1]表示决策者对于方案i的偏爱程度,[v-ij,v+ij]⊂[0,1]表示决策者对于方案j的偏爱程度,且0≤μ+ij+v+ij≤1,记Θ为区间直觉模糊集。由概念可知,最大模糊数为α+=([0,0],[1,1]),α-=([0,0],[1,1]),α的得分函数记为:
(3)
定义3[9]:设X是一个非空论域,对于两个区间直觉模糊集A和B,根据熵的概念定义A和B相似度为S(A,B),表达式为:
(4)
其中:
μ-j=|μ-A(xj)-μ-B(xj)|,v-j=|v-A(xj)-v-B(xj)|
μ+j=|μ+A(xj)-μ+B(xj)|,v+j=|v+A(xj)-v+B(xj)|
若在考虑每个方案属性权重的情况下,令ωi作为每个属性Xj∈X的权重,那么两个区间直觉模糊集A和B的权重相似度公式为:
(5)
2 节水灌溉工程方案优选模型
2.1 区间直觉模糊熵权法确定属性权重
信息熵是由Shannon首次提出的,在熵的基础上引入信息论思想的一个热力学概念[10]。熵值不仅可以进行信息无序度和混乱度的描述,而且可以用来衡量信息量的大小。进行节水灌溉工程方案决策时,各工程方案在某个属性的属性值模糊程度越小,其含有的信息量越大,该属性对于方案决策的作用也随之增大,且该属性对应的信息熵值也越小,决策信息系统的无序化程度减弱。因此可以用信息熵来度量各方案对应属性的信息量,进而确定各属性的相应权重。
根据信息熵的思想,本文在区间直觉模糊环境下提出了区间直觉模糊熵权法来确定属性权重,属性值的信息熵也被赋予新的含义。一个区间直觉模糊数的模糊程度称作它的犹豫度,可以通过其得分函数来反映。因此,本文在权重信息完全未知的情况下从得分函数出发,通过计算区间直觉模糊环境下各属性的平均信息熵从而得到相关属性权重大小。与传统的单目标优化模型求解多属性决策问题权重相比,该权重求解方法更为简便,也更易于实现。
Shannon创立信息论的时候,将一个离散信源的不确定性通过随机变量F的先验概率分布P={p1,p2,…,pn}来描述,且0≤pi≤1,∑pi=1,i=1,2,…,n。该离散信源的平均不确定性定义为[11]:
(6)
式(3)中,常数k一般由属性单位来决定,通常取k=1,对数函数的底通常取2、10或e,本节中以常数e作为对数函数的底。设F=[αij]n×m为一个区间直觉模糊决策矩阵,αij=(μij,vij)为区间直觉模糊数,对于每一个节水灌溉工程方案Ai(i=1,2,…,n),计算方案Ai关于属性Xj的特征信息的得分函数值并进行归一化处理:
(7)
进而求出各属性Xj的平均信息熵:
(8)

(9)
2.2 区间直觉模糊TOPSIS决策模型构建
TOPSIS法又称优劣解距离法,其基本原理是通过确定正、负理想解,测算决策评价对象与正理想解(最优解)和负理想解(最劣解)的距离并进行排序,从而判断最佳决策对象的一种方法。若决策对象与正理想解的距离最近同时与负理想解的距离达到最远,则称该决策方案为最优方案,否则为最差方案。本文结合区间直觉模糊集原理,将TOPSIS法与区间直觉模糊集法相结合,利用上文中区间直觉模糊集的相似度公式(4)、(5)来度量决策对象与正、负理想解之间的相似度,最终对相似度排序确定最优节水灌溉工程方案,其相较于以往的度量公式更为客观有效,充分考虑了不完全信息下的多目标节水灌溉工程方案决策问题。
设A={A1,A2,…,An}为节水灌溉工程方案集,X={X1,X2,…,Xm}为属性集,节水灌溉工程方案Ai关于属性Xj的评价可以通过区间直觉模糊集Fij=(μij,vij)来表示。令μij=[μ-ij,μ+ij]⊂[0,1]表示方案Ai∈A满足属性Xj∈X的程度,vij=[v-ij,v+ij]⊂[0,1]表示方案Ai∈A不满足属性Xi∈X的程度,且0≤μ+ij+v+ij≤1。Ai关于m个属性的属性值为:
Ai=(Fi1,Fi2,…,Fim)
={[μi1,vi1],[μi2,vi2],…,[μim,vim]}
(10)
因此,节水灌溉工程方案优选问题可以通过决策矩阵F=[(μij,vij)]n×m来表示。根据TOPSIS的基本思想,区间直觉模糊TOPSIS决策方法的具体算法如下。
(1)确定正、负理想方案A+和A-:
A+={〈[μ-1+,μ+1+],[v-1+,v+1+]〉,…,〈[μ-n+,μ+n+],[v-n+,v+n+]〉}
(11)
A-={〈[μ-1-,μ+1-],[v-1-,v+1-]〉,…,〈[μ-n-,μ+n-],[v-n-,v+n-]〉}
(12)
其中,∀j=1,2,…,n,且:
〈[μ-j+,μ+j+],[v-j+,v+j+〉=〈[maxiμ-ij,maxiμ+ij], [miniv-ij,miniv+ij]〉
〈[μ-j-,μ+j-],[v-j-,v+j-〉=〈[miniμ-ij,miniμ+ij], [maxiv-ij,maxiv+ij]〉


(4)根据式(9)计算出各属性Xj的权重系数ωj,j=1,2,…,n;
(5)根据式(5)分别计算Ai与A+的相似度S(Ai,A+),Ai与A-的相似度S(Ai,A-):
(14)
(6)计算方案Ai相对于A+和A-的相对相似度S(Ai):
(15)
(7)根据相似度S(Ai)(i=1,2,…,n)的大小,按从大到小的顺序对节水灌溉工程方案Ai∈A进行排序。相似度越大,对应的工程方案越优。
3 算例分析
目前,随着我国环保形势的日益严峻,国家正大力发展农田水利节水灌溉技术,在各大灌区开展多项节水灌溉工程。某灌区节水灌溉工程现有如下四个建设方案可供选择:管道灌溉、喷灌、滴灌和小管出流灌溉(记为A1,A2,A3,A4)。各节水灌溉工程涉及到多个子工程系统,具有多因素影响、多主体等特点,由于节水灌溉工程的这种复杂性和不确定性,专家在对工程方案进行优选决策时评价指标的数据往往无法精确到具体的测度值,而只能通过区间数来表示。节水灌溉工程优选指标从国民经济、技术、社会3个层面来考虑,国民经济层面包含净现值、收益率、投资回收期、效益费用比4个指标;技术层面包含灌水均匀度、灌溉水利用率两个指标;社会层面包含作物适应性、农民欢迎程度、便于施工程度3个指标,按顺序标记为C1,C2,…,C9,具体评价指标见表1[12,13]。
Step1:根据公式(11)、(12)确定正、负理想方案A+和A-,具体计算结果见表2。
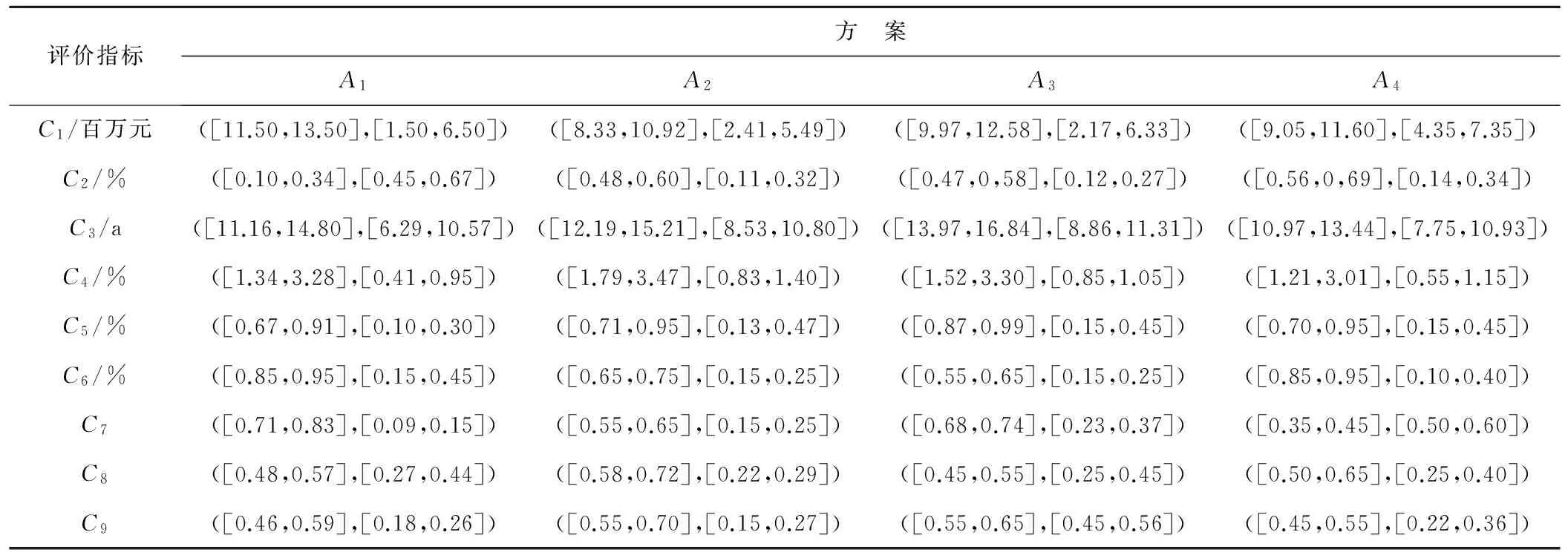
表1 各方案评价指标值

表2 正负理想方案及各指标权重
Step2:根据公式(7)~(9)计算各评价指标的区间直觉模糊熵权:
ω=(0.121 7, 0.123 9,0.104 0,0.085 9, 0.109 4,
0.113 5, 0.124 6, 0.108 3,0.106 9)
Step3:根据式(13)、(14)分别计算方案Ai与A+的相似度S(Ai,A+),Ai与A-的相似度S(Ai,A-),求出:
S(A1,A+)=2.893 6,S(A2,A+)=2.450 5,
S(A3,A+)=2.329 9,S(A4,A+)=2.571 0
S(A1,A-)=1.652 6,S(A2,A-)=2.385 5,
S(A3,A-)=2.206 9,S(A4,A-)=2.007 7
Step4:根据式(15)计算方案A1,A2,A3,A4相对于A+和A-的相对相似度S(Ai),i=1,2,3,4。
S(A1)=0.584 0,S(A1)=0.516 4,
S(A1)=0.441 7,S(A4)=0.520 3
Step5:将S(A1)、S(A2)、S(A3)、S(A4)按从大到小的顺序排列从而确定节水灌溉工程方案的优劣,排序结果为:A1>A4>A2>A3,即方案1管道灌溉为最优方案。
在文献[12,13]中由于权重确定方法以及方案优选决策模型不同,各属性的相对权重大小与本文有所偏差,但最后计算得出的节水灌溉工程方案优选结果基本一致,最优方案都为管道灌溉。
4 结 语
节水灌溉工程方案优选是一个复杂得多属性决策问题,涉及诸多影响因素。本文提出了一种基于区间直觉模糊TOPSIS法的节水灌溉工程方案优选方法,通过区间直觉模糊集来描述属性的模糊信息,并利用区间直觉模糊熵权法确定权重,通过判断不同工程方案的相对相似度大小对方案进行优劣排序,最终确定最佳节水灌溉方式。本文的研究既是对区间直觉模糊集与传统TOPSIS法的改良,也是该方法在节水灌溉工程方案优选领域的新应用。研究表明,该方法充分利用了原始数据信息,能够比较准确地对工程方案进行判断,同时可以应用于其他水利工程问题的评价优选和分类决策,具有较强的实用价值。
[1] 罗世良,陈振存.基于投影寻踪模型的节水灌溉工程方案优选[J].地下水,2009,31(5):93-111.
[2] 郭法强,杨昕馨,姚鹏亮.TOPSIS模型的节水灌溉方案优选[J].水利与建筑工程学报,2009,7(3):84-86.
[3] 高军省.节水灌溉方案优选的集对分析方法[J].节水灌溉,2010,(12):81-83.
[4] 郭文献,徐建新,卢双宝.模糊物元模型在节水灌溉方式优选中的应用[J].中国农村水利水电,2006,(5):27-29.
[5] 刘 森,于雪峰.模糊聚类在节水灌溉方案优选中的应用[J].黑龙江水利科技,2014,42(4):21-23.
[6] Atanassov K, Gargov G. Interval valued intuitionistic fuzzy sets[J].Fuzzy Sets and Systems.1989,31(3):343-349.
[7] 娄 帅,王慧敏,牛文娟,等.基于区间直觉模糊集的水资源配置群决策研究[J].长江流域资源与环境,2014,23(3):320-327.
[8] 徐泽水,陈 剑.一种基于区间直觉判断矩阵的群决策方法[J].系统工程理论与实践,2007,27(4):126-133.
[9] WEI Cui-ping, WANG Pei, ZHANG Yu-zhong. Entropy, similiarity measure of interval-valued intuitionistic fuzzy sets and their applications[J].Information Sciences,2011,181:4 273-4 286.
[10] 马黎华,康绍忠,粟晓玲.西北干旱内陆区石羊河流域用水结构演变及其驱动力分析[J].干旱地区农业研究,2008,26(1):125-129.
[11] 吴 冲,万翔宇.基于改进熵权法的区间直觉模糊TOPSIS方法[J].运筹与管理,2014,23(5):43-47.
[12] 邓丽娟,马爱玲.基于CRITIC权重与YOPSIS模型的节水灌溉方案优选[J].水科学与工程技术,2010,(2):10-11.
[13] 门宝辉.选择节水灌溉方式的灰色关联投影法[J].沈阳农业大学学报,2004,35(5):476-479.

