微喷头水量分布仿真及组合优化研究

刘晓扬，杨路华，柴春岭，康 浩

(河北农业大学，河北 保定 071001)

单微喷头的水量分布特性除了与微喷头自身性能有关外，还与微喷头的安装高度和工作压力等有密切关系。微喷灌灌水质量的好坏通常以喷灌组合均匀系数作为评价指标，喷灌组合均匀系数是指喷灌面积上水量分布的均匀程度。喷灌组合均匀系数关系到作物长势是否均匀，是否产生径流、水洼，导致水土流失或是水资源浪费，喷灌组合均匀系数过高又会造成投资成本的升高和能源的浪费。

微喷灌在进行组合喷洒时，插杆高度需要多高？工作压力需要多大？组合间距为多少时喷灌组合均匀系数能达到最佳效果，则需要通过电子计算机以及科学的计算方法求得。我国从20世纪80年代开始通过电子计算机分析微喷头水力性能及规划设计中的应用。邓鲁华(2003年)利用Delphi语言和解析算法编制软件，进行单喷头实验数据处理及多喷头组合喷洒分析，实现了结果可视化[1]；张志宇[2](2006年)运用Matlab径向神经网络研究了基于径向基模型的组合喷灌均匀系数的计算，然后通过遗传算法进行组合最优化，得出最优组合间距；韩文霆、劳冬青[3](2007年)将Visual C++和Matlab工具整合起来，开发了喷头水量分布仿真和喷头组合优化分析系统；西北农林科技大学的张洋[4](2012年)以C#和OpenGL为开发语言，开发了一套集喷头水力性能和喷灌系统评价的软件系统，可以计算出给定的任意组合形式和组合间距进而求得组合均匀度。

以上研究均对大射程喷头进行了组合优化，对于微喷头来说，微喷头安装高度也是影响水量分布的因素之一，因此，研究微喷头安装高度、工作压力与组合间距共同作用下对水量分布的影响，也是微喷头组合优化的一部分，对微喷灌系统的投资有重要影响。

1 微喷头水量分布试验

单微喷头雨量筒的布置形式有网格式和射线式2种，网格式的雨量筒布置形式又分为2种：第一种是雨量筒在每个网格的中间，第二种是雨量筒在网格的4个角上，而网格式布置的缺点是需要布置的雨量筒个数繁多，按照每个网格间距0.5 m计算，如果是8 m×8 m的喷洒区域则需要289个雨量筒，雨量筒太多还会造成不必要的误差，通常试验采用射线法。射线法可以采用8条或12条射线。本试验采用射线法布置雨量筒，共布置12条射线。

试验选取WPX90-250型微喷头，以微喷头安装高度和工作压力作为试验设计的影响因素。安装高度取30、60、90 cm 3种方案，工作压力取0.15、0.20、0.25 MPa 3种方案。

2 水量分布网格化处理

2.1 克里金插值法进行网格化

采用射线法收集到的数据不能直接用于微喷头的叠加计算，必须经过插值运算标准化为方格状才能使用矩阵进行叠加计算。本文采用surfer软件进行微喷头数据的插值运算。Surfer软件提供12种数据网格化方法，包括加权反距离法、克里金法、最小曲率法、改进谢别德法、自然邻点法、最近邻点法、移动平均法等，根据试验所测数据和surfer软件中网格化方法的特点，点数据在小于250个时适用于用克里金法，本文采用克里金插值法进行网格化计算。

克里金插值法的计算公式如下：

(1)

其中点(x0,y0)处的估计值就是权重系数。采用加权求和法通过已知点的数据来估计待插点的值。与一般插值算法不同的是，克里金插值法的权重系数是估计值与真实值z0的最小差值的一套最优系数，而并非距离的倒数，即

minλiVar(z*0-z0)

(2)

无偏估计的满足条件为

E(z*0-z0)=0

(3)

2.2 Surfer软件的基本操作

原始数据的输入格式为X、Y、Z的excel或文本格式，X、Y为确定水量分布图的坐标点，Z为测点的点喷强，如图1。通过GRID程序，将原始数据转化为grd数据，由它生成水量分布图。在这一操作中，可以通过弹出的窗口选择所需要的网格化方法，还可以查看并修改用到的数据，在网格线素几何学中可以对网格间距进行调整。在软件的主菜单地图项，打开等值线图或在软件右边的工具栏选择等值线图，选择需要显示的grd数据，该数据的水分布图就会显示出来。打开线框图，则会显示该数据下的三维水量分布图。选择GRID里的Extraction项，提取生成的网格化数据并保存为dat格式文件。

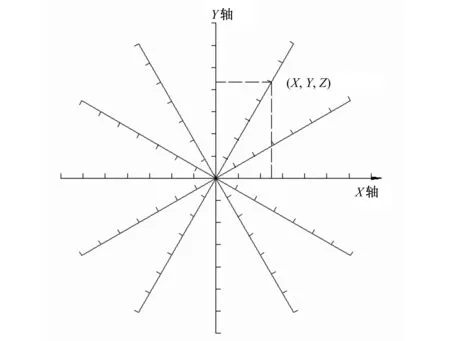
图1 数据转化示意图Fig.1 The sketch map of data transformation

3 基于Matlab对微喷头水量分布进行组合间距优化

叠加法是计算组合均匀系数的传统方法，这种方法缺点是需要人工将测得的喷洒强度绘制在纸上，在进行叠加时，水量分布曲线也并不一定会在中心点处交叉，还需要人为的估算，这种方法并不精确，而且求最优组合间距时工作量巨大不易完成。

文中微喷头采用矩形布置进行组合优化。优化系统以投资作为优化目标，及喷头间距和支管间距所围成的典型面积最大为目标；约束条件设定为组合均匀系数大于75%小于85%、喷洒强度大于4 mm/h小于12 mm/h。

3.1 最优典型面积确定

如果说典型面积的选择是计算微喷头组合均匀度必要的条件，有效微喷头的确定则关系到计算的精度问题。典型面积分为以微喷头为中心，四周包围的面积作为典型面积，另一种是以喷头为角点所包围的面积为典型面积。如图2，根据陈学敏[5](1981年)的试验研究，采用图2(b)较为合理，因为该方法所需要的微喷头个数较少，这样可以减少一些工作量。

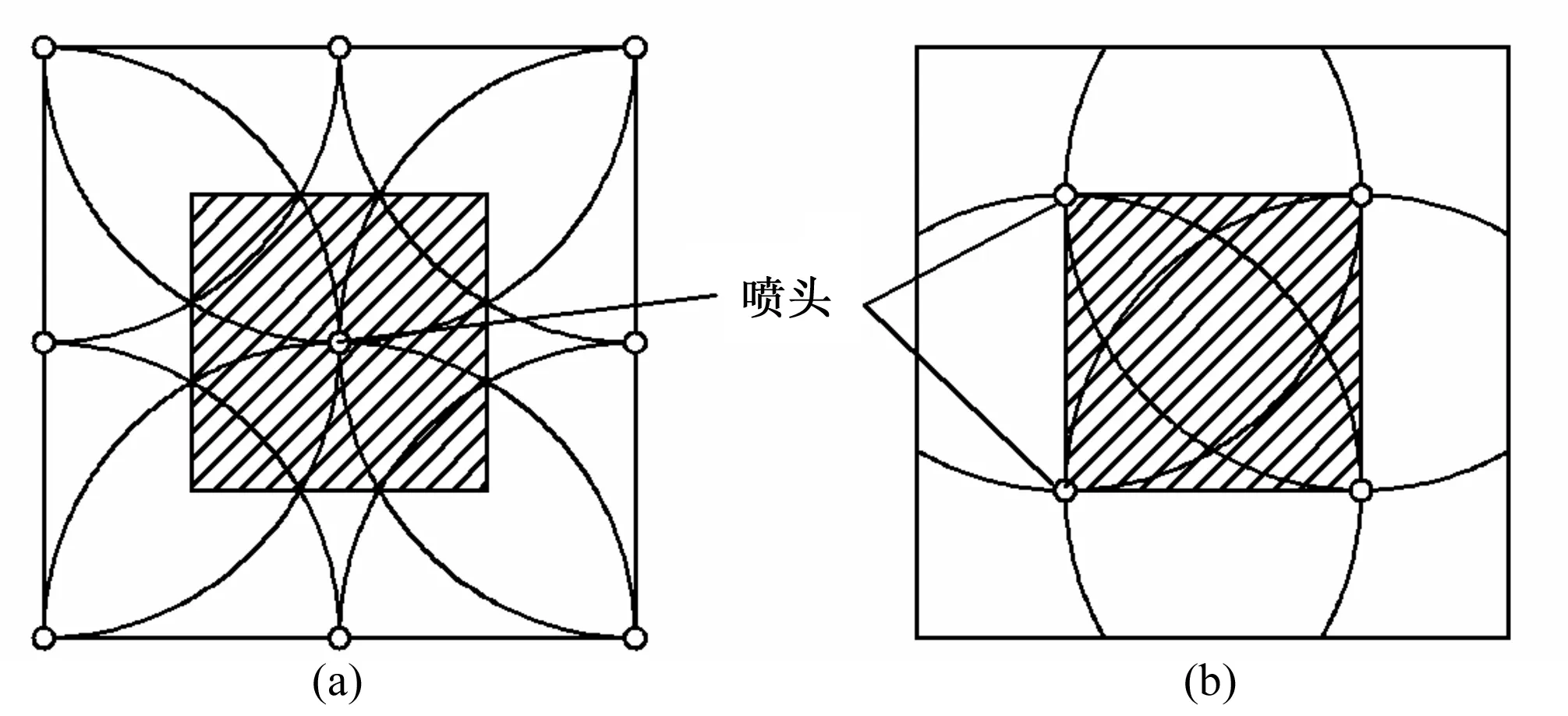
图2 典型面积示意图Fig.2 The sketch map of typical area

3.2 矩阵叠加个数

典型面积的水量叠加表示为矩阵叠加，但矩阵相加的个数随着支管间距和微喷头间距的不同而不同[6]。最极端的两种情况：一种是无论支管间距还是微喷头间距，最长不会超过微喷头的有效喷洒直径，因为这种情况下典型面积就已经出现了漏喷。另一种情况是支管间距或者微喷头间距无限接近最小，典型面积就会受到较多的微喷头影响。本文讨论的典型面积内水量最多受16个微喷头的影响，也就是说喷头沿支管的间距不大于0.5倍有效喷洒半径R[7]，如果微喷头间距太小会增加不必要的投资，而且组合间距太小时，喷洒强度大，可能产生径流。

3.3 典型面积的矩阵叠加

单微喷头射线法测得的数据经过插值化后，可以表示为一个矩阵形式Xn×n，为了方便以后叠加计算，n在数值上以微喷头在最大压力下的有效喷洒直径为行数或是列数，记为：

Xn×n=[eij]n×n

(4)

在程序编制过程中，只考虑微喷头间距或是支管间距在0.5R到2R之间的变化。首先将微喷头支管距离定为0.5R，让微喷头间距从0.5R到2R变化，变化幅度为一个网格节点，并计算出每个组合下的平均喷洒强度和组合均匀系数；然后让支管间距增加一个网格节点，再让喷头间距从0.5R到2R变化，依次循环，直到支管间距和微喷头间距都达到2R时结束。图3为矩形组合叠加示意图。

图3 矩形组合叠加示意图Fig.3 The sketch map of rectangle combination

3.4 组合间距优化程序设计

for循环是最常用的程序语句，通过for循环可以简化编写程序。因为典型计算面积的a和b都是变化的，所以可以套用两个for循环语句，以微喷头间距和支管间距都最小为例。16个微喷头喷洒在典型计算面积中的数据分别记为矩阵A，B，…，O，P。先以微喷头间距a为固定值，a取1.5 m，支管间距b从1.5 m到8 m变化，每次增加0.1 m。例如当支管间距和微喷头间距都为8 m时，1、2、5、6号喷头叠加到典型计算面积内的区域示意图如图4。

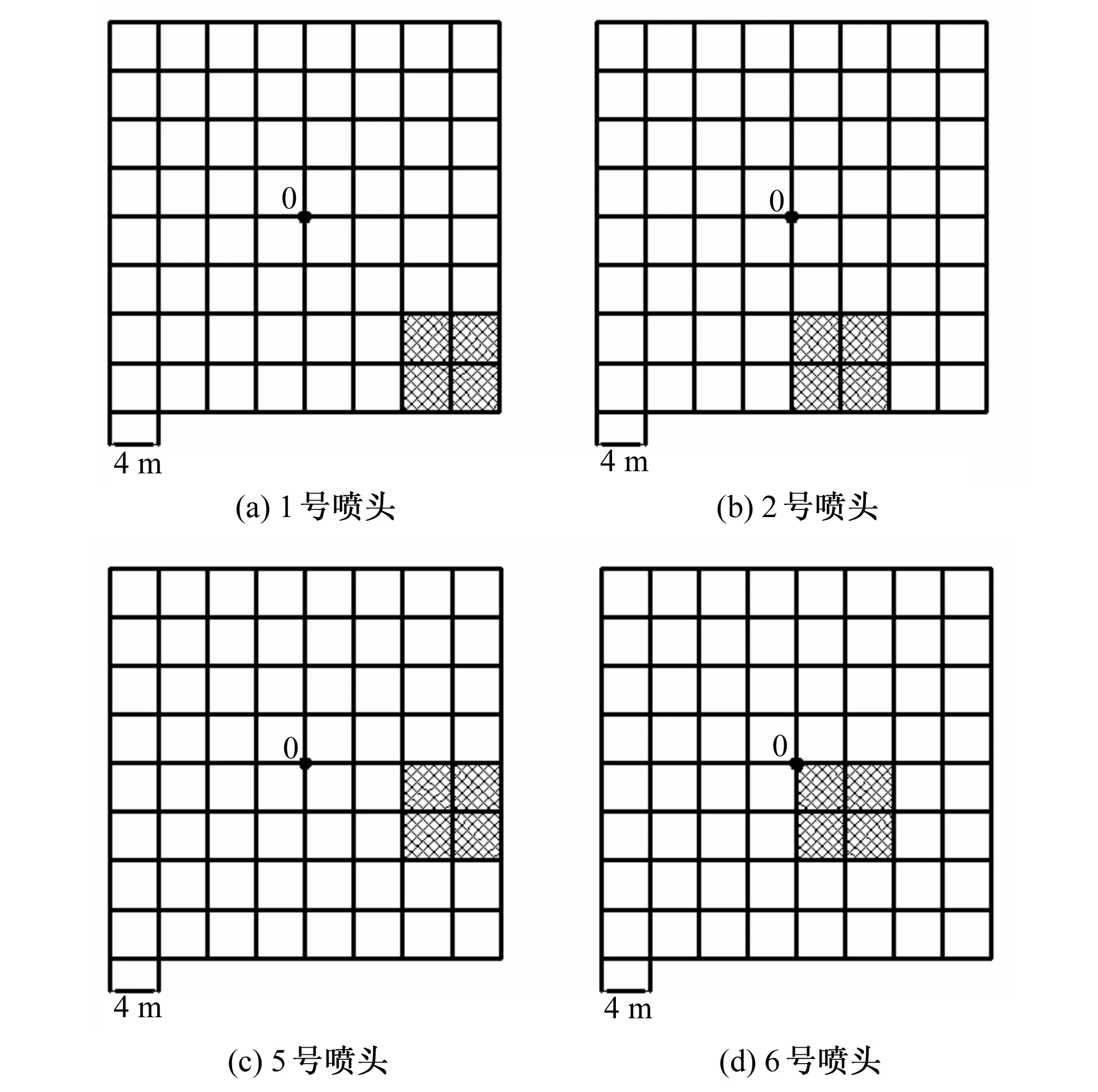
图4 矩形组合4个喷头作用区域示意图Fig.4 The function area of sprinklers spaced in

3.5 组合优化实例

以微喷头安装高度为30 cm、工作压力为0.15 MPa为例，进行单喷头射线法水量分布试验。通过Surfer软件将射线法数据转化为网格化数据，通过Matlab软件对网格化数据进行组合优化，结果见表1。

典型面积越大，单位面积内的喷头个数越少，投资也就越低。在均匀系数和喷洒强度均在约束范围内时，将典型面积从大到小排序，结果显示，喷头间距4.3 m，支管间距1.7 m时组合效果最优。

3.6 组合优化结果

表2为微喷头在3种安装高度和3种工作压力下的组合优化结果。由表2可知，3个安装高度的典型面积在工作压力为0.20 MPa时均达到最大，也就是说微喷头在工作压力0.20 MPa下的投资最小；在工作压力为0.20 MPa时，安装高度为60 cm时典型面积最大，可见安装高度不能过低也不可以过高；工作压力在0.15和0.20 MPa下喷洒强度基本相同，没有明显变化；工作压力在0.25 MPa下喷洒强度要大于0.20 MPa下的喷洒强度，而0.25 MPa下的典型面积要小于0.20 MPa下的典型面积，这说明微喷头在工作压力0.25 MPa下的喷洒效果没有0.20 MPa下的好。WPX90-250型微喷头进行组合微喷灌，微喷头安装高度可以取60 cm，工作压力取0.20 MPa，这样效益可以达到最佳值。

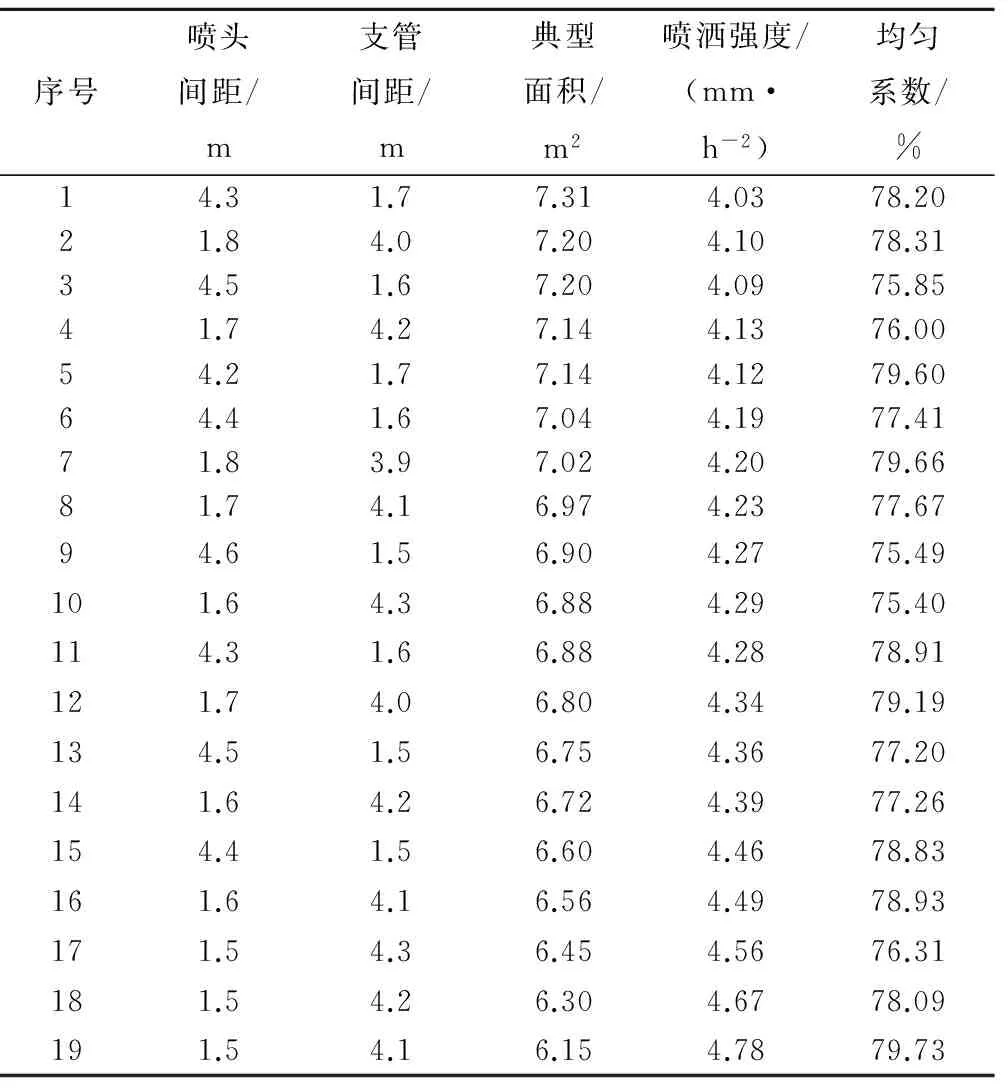
表1 安装高度30 cm、工作压力0.15 MPa下的组合优化结果Tab.1 Combined optimization results under installation height 30 cm and working pressure 0.15 MPa

4 结 论

通过surfer软件和Matlab软件求最佳组

表2 微喷头组合均匀系数与喷洒强度Tab.2 The uniform coefficient and spraying intensity of the micro-sprinkler

合间距，可以简化工程量，提高计算速度和准确度。把微喷头安装高度、工作压力和最佳组合间距考虑在最优化里，使得微喷头最优化更为合理，更趋近于实际。WPX90-250型微喷头进行组合微喷灌，可取工作压力0.20 MPa，安装高度60 cm，通过组合优化可以达到WPX90-250型微喷头的最佳喷洒效果。

[1] 邓鲁华,郝培业.基于Delphi的喷头喷洒分析软件[J].山东理工大学学报(自然科学版),2003,17(3):33-36.

[2] 张志宇.喷头水量分布的智能仿真与组合间距的优化[D]. 河北保定：河北农业大学,2006.

[3] 韩文霆,劳冬青.圆形或异形喷洒域喷头组合均匀度分析系统V1.0,软件登记号:2007SR18122,2007.11.17.

[4] 张 洋.基于C#与OpenGL喷头水量分布动态模拟及组合优化[D].陕西杨凌：西北农林科技大学,2012.

[5] 陈学敏.用电子计算机计算组合喷洒强度和均匀度[J].喷灌技术,1981,(1):6-12.

[6] 李小平,罗金耀. 单喷头水量分布的三角形组合均匀度叠加计算[J]. 水利学报,2005,(2):238-242.

[7] 李小平.喷灌系统水量分布均匀度研究[D].武汉:武汉大学,2005.