基于Feddes模型的干旱区滴灌幼龄枣树根系特征数值模拟
马 亮,魏光辉,王 婷,马英杰
(1.新疆农业大学水利与土木工程学院,乌鲁木齐 830052;2.新疆塔里木河流域管理局,新疆 库尔勒 841000)
0 引 言
新疆南疆地区位于塔里木盆地边缘,具有典型的“沙漠绿洲,灌溉农业”特性,水资源极度匮乏,自然生态环境极其脆弱。如何利用有限的水资源发展农业,是目前面临的重大问题。采用高效节水灌溉技术是降低农业用水总量、调整农业用水结构的有效方法[1,2],而制定合理的灌溉制度则是实现农业可持续发展的重要保证。由于根系是作物吸收水分和养分的主要器官[3],研究滴灌条件下的枣树根系分布规律,将为制定干旱区枣树灌溉制度,提出增产、节肥与节水相协调的大田水分管理模式提供重要参考。
目前,前人对成龄枣树不同灌溉方式下的根系分布特征进行了初步研究,也取得了一定的研究成果。如,李宏等[4]通过对成龄枣树根系的研究,揭示了根系在漫灌条件下土壤空间分布规律;郭光华等[5]对漫灌方式下的盛果期红枣根系分布特征进行了定量研究,结果表明水平距离0~200 cm和垂直深度0~70 cm以内土层是枣树田间水肥管理的重要区域,土壤质地是影响根系分布的重要因素之一;田盼盼等[6]对滴灌和沟灌方式下的枣树根系进行分析,结果发现滴灌可增加根系生物量,提高根系吸收水分和养分的能力。上述研究主要集中于成龄枣树根系特征分析,而对幼龄期枣树采用滴灌方式灌溉下的根系特征研究则鲜有报道[7]。鉴于此,本文以新疆塔里木盆地西缘的阿克苏地区为例,以当地滴灌幼龄枣树为研究对象,根据实测枣树根系分布、作物腾散量和根域土壤含水率变化数据,建立二维Feddes根系吸水模型,利用无网格法结合MATLAB软件编程模拟土壤含水率变化,探讨根系密度分布函数的适用性及其对幼龄枣树根系吸水的影响,以期为干旱区枣树节水灌溉制度的制定提供参考。
1 材料与方法
1.1 研究区概况
研究区位于新疆阿克苏地区红旗坡农场新疆农业大学林果实验基地内(地理坐标为80°14′E,41°16′N),属暖温带大陆性荒漠气候,年均气温11.5 ℃,相对湿度56%,日照时数2 855 h,年均降水量65.4 mm,水面蒸发量1 574 mm(E601蒸发器),无霜期207 d。研究区0~30 cm土层为砂壤土,30~120 cm土层为粉壤土,地下水埋深在20 m以下。幼龄枣树品种为灰枣, 2014年嫁接定植,树龄2年,株行距4 m×1 m,南北向种植,采用滴灌灌溉,在枣树两侧50 cm处各布设1根滴灌带,滴头间距30 cm,滴头流量1.75 L/h,设计工作压力为0.1 MPa。试验于2014年4月开展,共设1组处理,3次重复,各重复处理间设4 m的保护带。枣树各生育期灌水定额均为25 mm,全生育期灌溉定额为300 mm。在作物各生育期,结合当地农户管理经验,采用随水滴肥等方法为作物提供优良的生育环境。
1.2 试验设计
1.2.1土壤水分监测
红枣单作小区,在株间布设2个监测点,监测点相距30 cm;行间布设3个监测点,每个监测点相距25 cm,如图1所示。

图1 幼龄枣树根区土壤水分监测平面布置图(单位:cm)
土壤水分监测采用TRIME-IPH土壤水分测定系统测量其含水率(体积含水率,下同),灌前灌后均采集监测,每天北京时间10∶00人工测量,监测深度为0~100 cm(每10 cm测量一次土壤含水率,共计10层),监测期从4月20日开始至9月30日结束。
1.2.2根系采集与测定
假设枣树根系以树干为中心、在行间上的分布具有对称性,采用剖面法、分层取样测定根系生物量。选择3棵标准木,以枣树树干中心,垂直于树行方向,以标准木根部为起点,挖一条长1 m(沿行方向),宽0.4 m,深1.0 m的样带,水平方向为3个取样区,各取样区的范围分别距标准木0~0.2、0.2~0.3、0.3~0.4 m;垂直方向上每10 cm为一层分别进行取样。将所有土样破碎过筛,分装记录后带回室内。
土样过0.5 mm圆孔筛后,经冲洗、剔除杂质和死根后,置阴凉处晾干根表水分。然后用游标卡尺测量分选出根系直径大于2 mm和小于2 mm的根系,分称重记录后用EPSONTWAIN PRO(32 bit)扫描仪获取根系图像,利用Delta-t scan软件分析根长、根径等指标。
取样时间:2014年9月末,枣树为果实成熟期。
1.2.3吸收根的测定
本研究以直径2 mm以下的吸收根作为细根进行特征分析。
试验数据用Excel 2007,SPSS 19.0和Surfer 8.0软件进行数据处理。
2 模拟模型
2.1 土壤水分特征曲线
土壤水分特征曲线是表征土壤含水率与其水势关系的重要指标,通常采用Van Genuchten方程[8]求解,即:
(1)
K=KsSle[1-(q-S1/me)m]2
(2)

(3)
m=1-1/n,n>1
(4)
式中:θ为土壤体积含水率,cm3/cm3;θs为饱和体积含水率,cm3/cm3;θr为残余体积含水率,cm3/cm3;h为土壤水势,cm;a为进气值倒数;n为孔径指数;m为方程参数;l为经验系数,一般取0.5;K为非饱和导水率(渗透系数),cm/d;Se为有效体积含水率,cm3/cm3。
采用RETC拟合特征曲线方程的相关参数,根据实测土壤饱和导水率,计算得饱和体积含水率θs为0.39 cm3/cm3、残余体积含水率θr为0.07 cm3/cm3,α=0.042 cm,n=1.45、饱和导水率Ks为0.65 m/d、土壤田间体积持水量为0.362 cm3/cm3。
2.2 土壤水分运动方程
将土壤水运动概化为二维运移,采用改进Richards方程模拟[9],表达式为:
(5)
式中:θ为土壤体积含水率,cm3/cm3;h为土壤负压水头,cm;r为径向距离,cm;z为土壤深度,cm;t为模拟时间,d;K为渗透系数,cm/d;S(r,z,t)为根系吸水项,1/d。
2.3 枣树根系吸水函数
依据Feddes吸水模型建立根系吸水项 :
S(r,z,t)=r(h)b(z)ETc
(6)
式中:ETc为作物蒸腾速率,cm/d;r(h)为土壤水分胁迫函数;b(z)为根系相对密度函数,cm-1。
(7)
式中:h1为作物根系吸水厌氧值,cm;h2为土壤初始基质势值,cm;h3为土壤末态基质势值,cm;h4为根系凋萎时土壤基质势值,cm。
利用Hydrus-2D软件模拟,计算得h1为-15 cm,h2为-30 cm,h3为-20 m,h4为-60 m。
2.4 根系密度函数
根系密度是影响根区土壤含水率的重要因素之一,准确表征根系分布对土壤含水率的模拟精度将会有重大影响。目前,常用的根系密度函数有指数函数、线性函数和分段函数等。
Raats[10]提出根系密度函数满足指数关系,且土壤表层根系密度最大,b(z)表示为:
b(z)=ae-az
(8)
式中:a为经验系数;z为根系深度,cm,下同。
Prasad[11]通过研究湿润土壤中根系分布,将根系密度函数表述为线性函数:
(9)
式中:L为根系最大深度,cm,下同。
Hoffman等[12]提出了分段根系密度函数:
(10)
3 结果与分析
采用Matlab软件进行编程[13],利用无网格方法结合牛顿迭代法[14]对式(5)进行求解。模型模拟深度为100 cm(即枣树最大根系深度),总模拟时间10 d,空间步长为20 cm,时间步长1 d,根系吸水模型采用Feddes等模型,枣树生育期平均蒸腾速率为2.5 mm/d。
3.1 枣树根系经验密度函数分析
幼龄枣树根系最大深度为100 cm,根据式(8)~(10)及实测分层根系密度值,利用SPSS 19.0统计软件可得到根系密度的指数函数表达式:
y=5.171e-0.061 7 x
(n=10,r=0.881,r0.01=0.765)
(11)
线性根系密度函数的表达式为:
y=1.338(1-0.0117z)
(n=10,r=0.907,r0.01=0.765)
(12)
分段根系密度函数的表达式为:

(13)
(n=10,r=0.658,r0.01=0.765)
分别利用式(11)~(13)计算0~100 cm土层中的枣树理论根系密度值,并与实测值进行比较(见表1)。由表1可知,实测根系密度与线性函数的拟合度最优,模型相关系数为0.907,通过了显著性水平为0.01的相关性检验(r0.01=0.765),平均相对误差为8.32%,均方根误差为0.206 mm/cm3;实测根系密度与分段函数的拟合度最差,模型相关系数为0.658,未通过显著性水平为0.01的相关性检验(r0.01=0.765),平均相对误差为19.67%,均方根误差为0.577 mm/cm3;指数函数的拟合度介于上述两种模型之间,模型相关系数为0.881,通过了显著性水平为0.01的相关性检验(r0.01=0.765),平均相对误差为11.74%,均方根误差为0.341 mm/cm3。因此,在缺乏实测资料的情况下,可根据线性函数和指数函数来模拟研究区幼龄枣树根系密度分布。
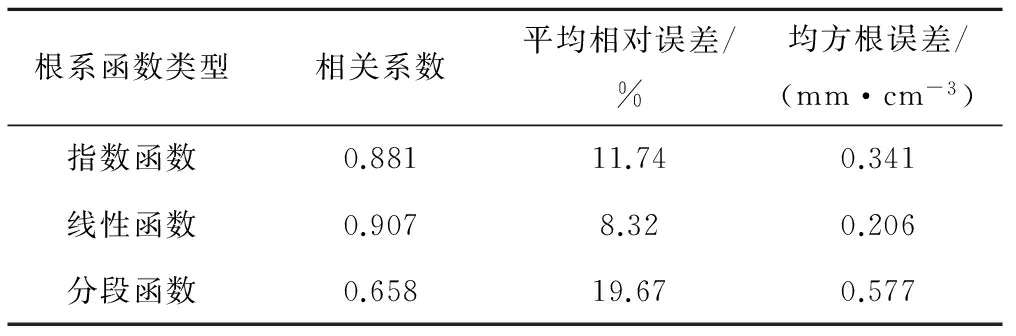
表1 不同根系密度函数模拟值和实测值误差分析
3.2 枣树根区土壤水分变化特征
由于滴灌条件下枣树根系有表聚化特征,故0~20 cm土层含水率变化主要受大气蒸发与根系吸水(即作物蒸腾作用)双重影响,而20 cm土层以下土壤含水率变化主要受根系吸水(即作物腾发)影响,因此,将拟合的枣树根系密度函数(指数函数、线性函数与分段函数)代入改进的土壤水分运动方程,即式(2),模拟不同土层土壤含水率变化。通过土壤含水率模拟值与实测值对比,利用相对误差、均方根误差等评价指标对不同根系密度函数的优劣性进行评判。图2显示了灌水前后,土壤含水率的模拟值与实测值对比情况。该图中,灌水时间为7月2日,土壤含水率取样时间为灌后第2天(即7月4日)和灌水后第7天(即7月9日)。

图2 不同根系分布函数下的土壤水分模拟值与实测值对比
为量化比较不同根系分布函数对土壤水分模拟值的影响,将3种根系函数下的土壤水分模拟值进行对比(结果见表2)。由表2可知,根系分段函数下的土壤水分模拟值和实测值误差相对较大,其中模型最大相对误差为9.94%,平均相对误差为5.67%,均方根误差为0.621;线性函数和指数函数下的土壤水分模拟值和实测值的误差值相对较小,模拟效果较优,其中线性函数最大相对误差为2.85%,平均相对误差为1.83%,均方根误差为0.238;分段函数最大相对误差为5.14%,平均相对误差为3.76%,均方根误差为0.423。因此,线性与指数根系分布函数可以较好地用于研究区幼龄枣树根系水分分布数值模拟。

表2 不同根系分布函数土壤水分模拟值和实测值误差分析
4 结 论
(1)采用线性函数、指数函数与分段函数分别对幼龄枣树根系分布特征进行模拟,结果表明:实测根系密度与线性函数的拟合度最优,模型相关系数为0.907,通过了显著性水平为0.01的相关性检验(r0.01=0.765),平均相对误差为8.32%,均方根误差为0.206 mm/cm3;实测根系密度与分段函数的拟合度最差,模型相关系数为0.658,未通过显著性水平为0.01的相关性检验(r0.01=0.765),平均相对误差为19.67%,均方根误差为0.577 mm/cm3。在缺乏根系实测资料的情况下,可采用线性分布和指数分布这两种经验函数来模拟根系分布。
(2)利用线性函数、指数函数与分段函数分别对幼龄枣树根系土壤剖面水分特征进行模拟,结果表明:分段函数下的土壤水分模拟值和实测值误差相对较大,其中模型最大相对误差为9.94%,平均相对误差为5.67%,均方根误差为0.621;线性函数下的土壤水分模拟值和实测值的误差值相对较小,模拟效果较优,其最大相对误差为2.85%,平均相对误差为1.83%,均方根误差为0.238。
(3)滴灌具有局部灌溉的特点,湿润土体范围有限,如何调整滴灌带与树体的距离,将对根系生长发育产生重要的影响。随着树体不断的生长,适当加大滴灌带的设计滴头流量和间距,将有利于扩大枣树根系生长的土壤空间范围,更好地吸收水分及养分。此外,本试验对象为3年幼龄果树,1年移栽种植,根系的生长发育存在对新移栽土壤环境的适应性,故根系分布范围较小。随着种植年限的增加,枣树的根生物量将会高于沟灌等传统地面灌溉,从而提高枣树吸收水分和养分的能力。
[1] 苏德荣.干旱地区间作种植高效节水灌溉基础问题研究[D].北京:中国科学院,2001.
[2] Wang X,Wang Z,Han Y,et al.Variations of fine root diameter with root order in Manchurian ash and Dahurian larch plantations[J].Frontiers of Forestry in China,2007,2(1):34-39.
[3] 杨林丰,钟 南.根系生长与土壤物理性状之间的关系[J].农机化研究,2007,(8):22-24.
[4] 李 宏,杨婵婵.幼龄期红枣根系生物量空间分布特征[J].中南林业科技大学学报,2013,(7):59-64.
[5] 郭光华,李 宏,李建贵.盛果期枣树根系空间分布规律研究[J].南方农业学报.2013,44(1):111-115.
[6] 田盼盼,董新光,姚鹏亮,等.干旱区不同灌溉方式下枣树根系分布特性研究[J]. 水资源与水工程学报,2012,23(1):102-105.
[7] 苏李君,王全九,白云岗.极端干旱地区葡萄根系吸水数值模拟[J].农业工程学报,2012,28(6):88-93.
[8] 雷志栋,杨诗秀,谢森传.土壤水动力学[M].北京:清华大学出版社,1988.
[9] 齐丽彬,樊 军,邵明安.紫花苜蓿不同根系分布模式的土壤水分模拟和验证[J].农业工程学报,2009,25(4):24-29.
[10] Raats P A C. Steady flows of water and salt in uniform soil profiles with plant roots[J]. Soil Sci Soc Am J, 1974,(38):717-722.
[11] Prasad R. A linear root water uptake model[J]. J Hydrol, 1988,(99):297-306.
[12] Hoffman G J, van Genuchten M T. Soil properties and efficient water use: water management for salinity control.In:Taylor H M, Sinclair T R(eds),Limitations to efficient water use in crop production[M]. American Society of Agronomy, Wisconsin, USA, 1983:73-85.
[13] 葛哲学.精通MATLAB[M].北京:电子工业出版社,2008.
[14] Wang Zhigang, Qin Xinqiang, Wei Guo, et al. Meshless method with ridge basis functions[J]. Applied Mathematics and Computation,2010,(217):1 870-1 886.

