冲积河流沙波阻力规律研究
董其华,赵连军,顾霜妹
(黄河水利委员会黄河水利科学研究院,水利部黄河泥沙重点实验室,郑州 450003)
河流阻力是水力学与河流动力学研究的基本问题,表征阻力的糙率是河流数学模型的关键参数。对于冲积性河道而言,河道床面形态在水流与泥沙的共同作用下不断调整,从而引起阻力的变化。床面形态是决定阻力大小的主要因素之一。冲积河流床面形态的调整主要表现为床面沙波或沙垄的形成、发展、消退与运移。
冲积河流动床阻力由床面阻力(沙粒阻力)和形态阻力(沙波阻力)两部分构成。而天然实测资料直接反映的是综合阻力,在沙波(垄)发展演变的过程中,可以认为床面阻力没有发生变化,只是形态阻力进行不断调整。
沙波阻力大小直接与沙波的几何形态尺寸相关,因此Vanoni-Hwang[1]、Chang[1]、郭俊克和惠遇甲[2]等根据实测资料建立了沙波阻力系数与沙波几何尺寸(波长λ及波高Δh)间的关系。但由此导出的方程式不能直接用来预报一定水流泥沙条件下沙波阻力的具体数值,还需要建立沙波尺寸与水流泥沙条件的关系[3]。有鉴于此,本文基于花园口河段沙波实测资料,通过对地形概化不同的精细程度,运用数学模型对不同比降下的不同沙波尺寸进行同流量沿程水位进行试算,直接计算综合阻力,然后根据分割法计算沙波阻力,研究冲积河流床面沙波阻力的规律。
1 天然床面形态
天然河道中的沙波几何尺度大小不一。从沙波的几何尺度来划分,主要存在沙纹、沙垄、沙丘等。但在许多情况下,床面为沙垄形态,因此本文主要研究沙垄床面的水流阻力。
图1绘制了黄河下游花园口河段实测沙垄纵剖面图[4],沙垄的高度与水深有密切关系,一般水深大的河流沙垄高度大,水深小的河流沙垄高度小,黄河下游河道相对宽浅,沙垄高度一般在1~2 m。图2点绘了黄河实测沙波高度与波长的关系图[4]。由此可见,总体趋势看,沙垄的波长随波高的增加而增大,特别是对于波高小于1.5 m的沙垄,波长与波高的关系非常明显,但当波高大于1.5 m以后,随着波长的增加,波高增长的速度不再明显。
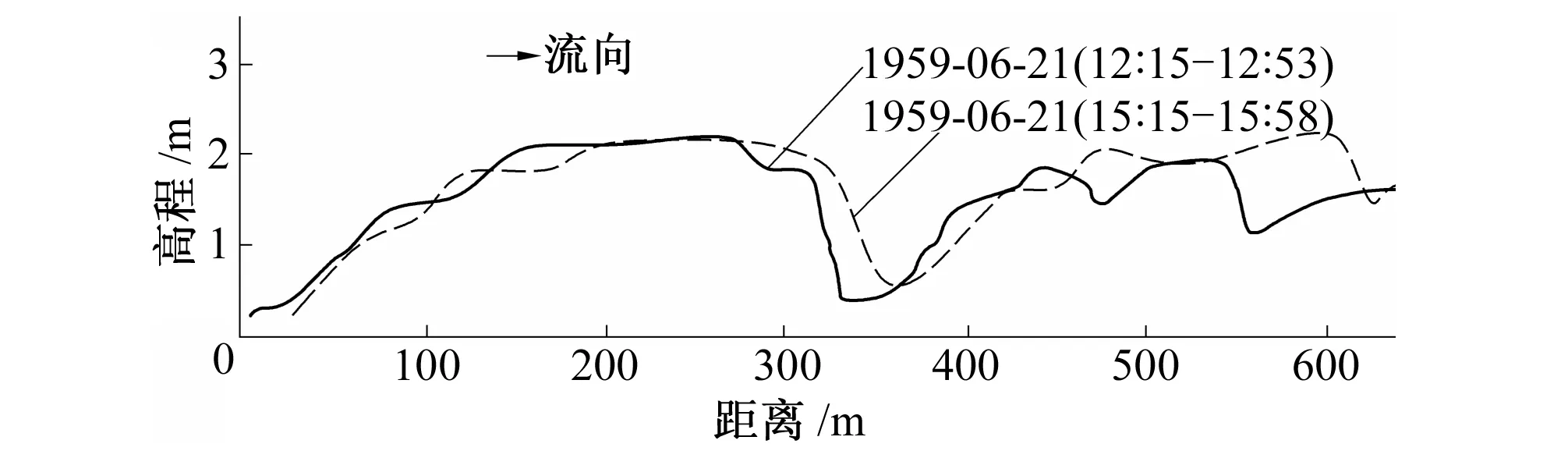
图1 黄河下游花园口河段沙垄纵剖面图Fig.1 Dune longitudinal profile of the lower Yellow River in Huayuankou

图2 黄河花园口河段沙垄波长与波高的关系Fig.2 Relationship between the dune wavelength and wave height of the lower Yellow River in Huayuankou
2 多沙河流沙波阻力规律研究
本次利用准二维非恒定流水沙数学模型对花园口河段不同尺寸沙垄进行概化计算。
2.1 数学模型概况
模型计算选用的描述水流与泥沙运动的基本方程为[5]:
水流连续方程:
(1)
水流运动方程:
(2)
式中:角标i为断面号;Q为流量;A为过水面积;t为时间;x为沿流程坐标;Z为水位;K为断面流量模数;α1为动量修正系数;qL为河段单位长度侧向入流量。
模型计算采用非耦合解法。方程(1)、(2)采用四点隐式差分格式离散。
2.2 计算概况
本次计算河宽为600 m,比降分别选用0.1‰、0.2‰。依据图2选取沙垄的波长及波高。表1列出了不同组次沙垄地形参数。

表1 不同组次沙垄地形参数对照表Tab.1 Parameters of different groups of dune terrain
具体的计算过程为:

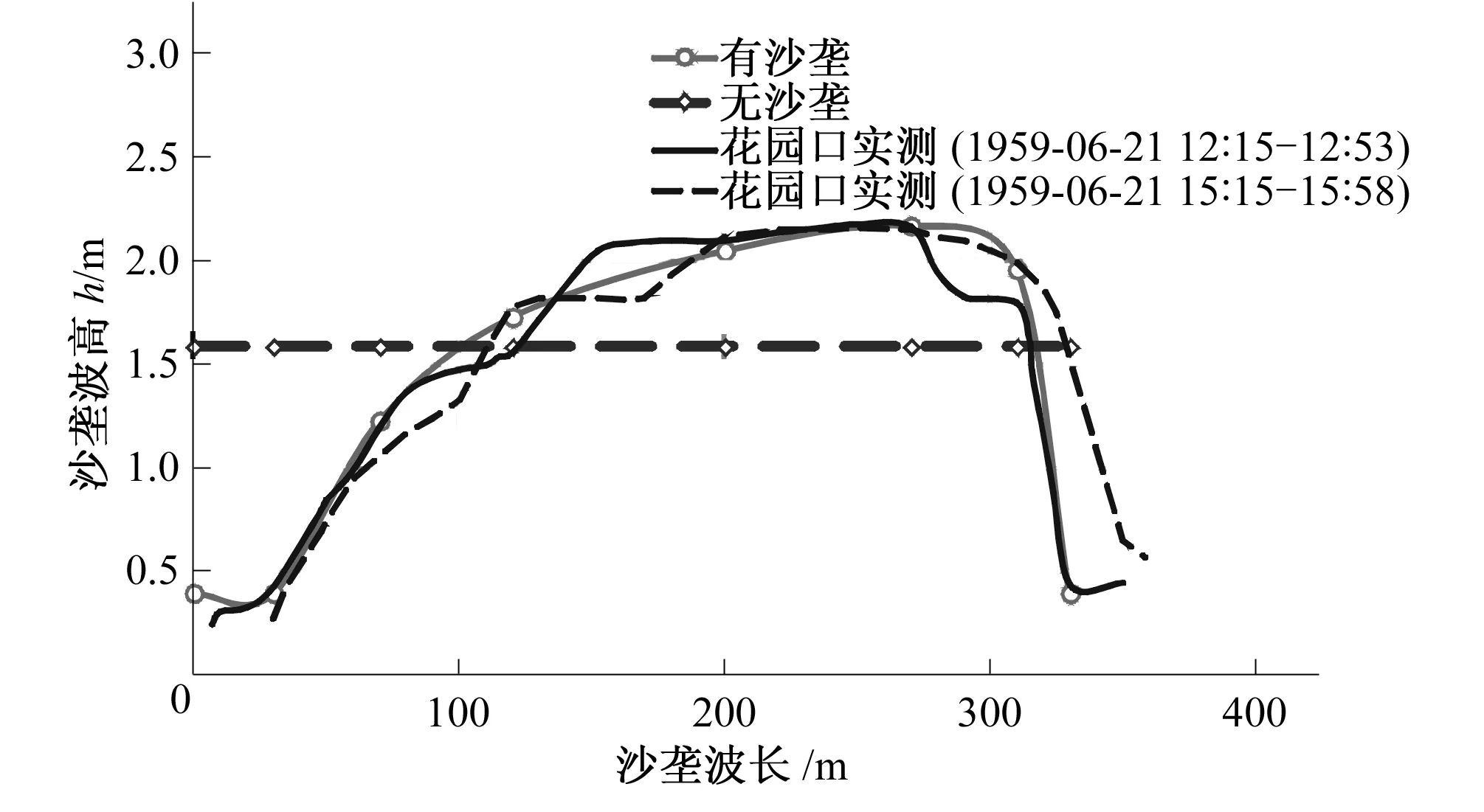
图3 有无沙垄沿程地形对比Fig.3 Terrain with and without dune
(2)依据计算区域内蓄水体相等原理,将各组沙垄地形概化为无沙垄的平整地形(图3),并按比降概化各组地形。进口单宽流量仍采用5 m3/s。给定上述沙垄地形沿程水位总比降与地形比降相同时的出口断面水位,调整综合糙率n,直至沿程水位总比降与地形比降相同。
2.3 计算结果

表2 采用能坡分割原则、水力半径分割原则计算的沙波阻力Tab.2 Form resistance by the energy slope partition theorem and the hydraulic radius partition theorem
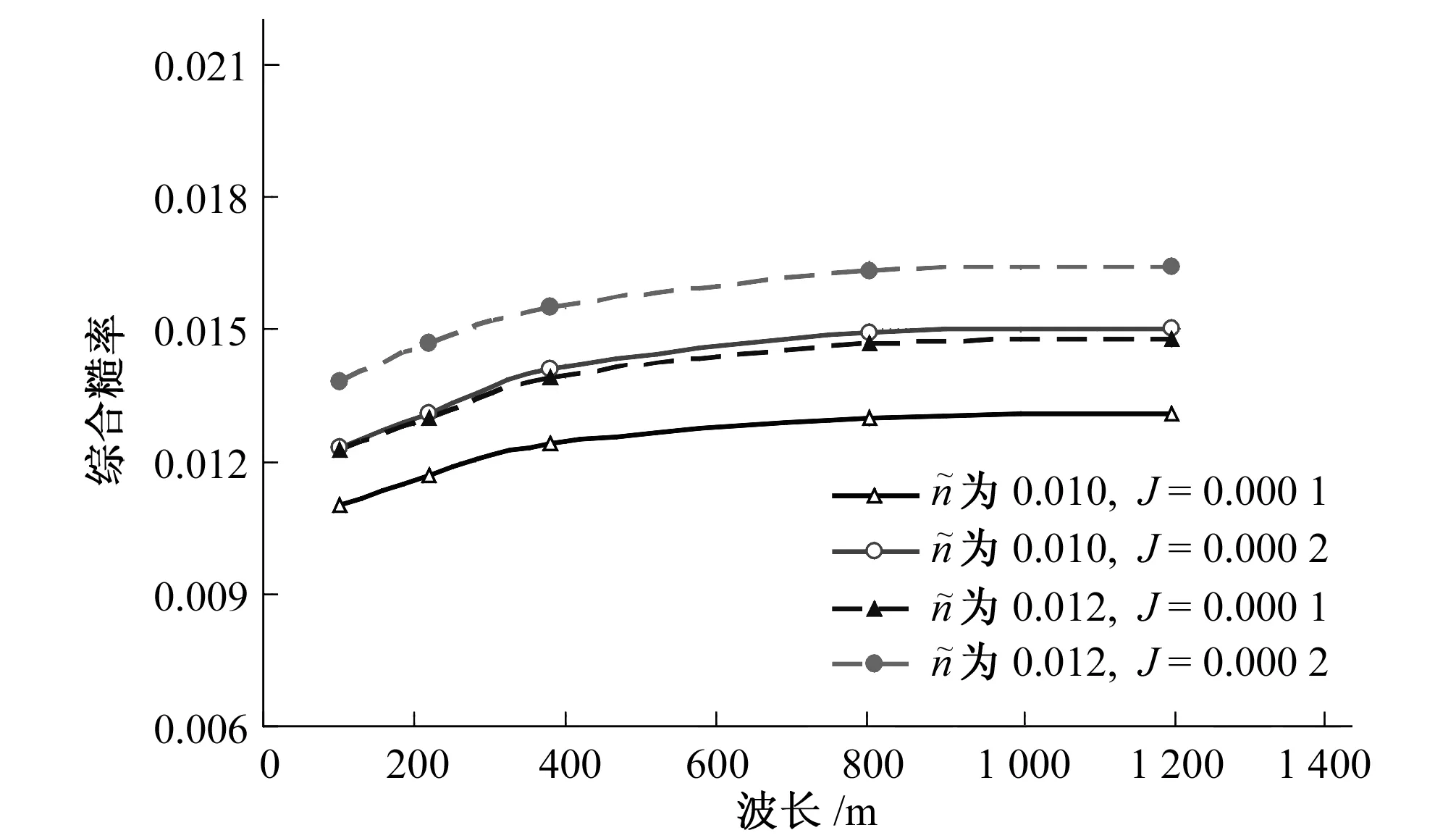
图4 综合糙率n随波长的变化Fig.4 Comprehensive roughness along with the change of wavelength

图5 沙波阻力随波长的变化Fig.5 Form roughness along with the change of wavelength
综上所述,在沙粒阻力一定时,综合阻力和沙波阻力均随波长λ的增大而增大,但增长的速度却随波长λ的增大而减小,波长超过800 m以后增长速度更慢;综合阻力和沙波阻力均随比降的增大而增大。
另外,将沙波阻力所占比例也列入表2。可以看出,沙粒阻力一定时,沙波阻力所占的比例随沙波的尺寸增大而增大,当波长增大到1 200 m时,沙波阻力所占的比例可以增大到50%左右;相同尺寸的沙波,沙粒阻力增加,沙波阻力所占比例相应减小。
3 结 论
本文基于花园口河段沙波实测资料,运用数学模型对不同比降下的不同沙波尺寸进行同流量沿程水位进行试糙,认为在床面阻力一定时,综合阻力和沙波阻力均随波长的增大而增大,但增长的速度却随波长的增大而减小,波长超过800 m以后增长速度更慢;综合阻力和沙波阻力均随比降的增大而增大;沙粒阻力一定时,沙波阻力所占的比例随沙波的尺寸增大而增大,当波长增大到1 200 m时,沙波阻力所占的比例可以增大到50%左右;相同尺寸的沙波,沙粒阻力增加,沙波阻力所占比例相应减小。
□
[1] 钱 宁,万兆惠.泥沙运动力学[M].北京:科学出版社,1983.
[2] 郭俊克,惠遇甲.沙垄阻力的理论分析与试验研究[J].水动力学研究与进展,1990,6(1):1-12.
[3] 黄才安,严 恺.动床阻力的研究进展及发展趋势[J].泥沙研究,2002,(4):75-81.
[4] 钱 宁,周文浩.黄河下游河床演变[M].北京:科学出版社,1965.
[5] 张红武,黄远东,赵连军,等.黄河下游非恒定数沙数学模型- 模型方程与数值方法[J].水科学进展,2002,(3):2-7.
[6] Chanson H, Qiao G. Drag reduction in hydraulic flows[C]∥ In: Aust IE ed. Proceedings of 1994 International Conference on Hydraulics in Civil Engineering, Brisbane, Australia, 1994L123-127.
——花园口电灌站的郑州记忆

