基于傅抱璞模型的岷江上游流域实际蒸散研究

尹铎皓，范雲鹤，周君华，刘铁刚

(四川大学水力学与山区河流开发保护国家重点实验室、四川大学水利水电学院，成都 610065)

0 引 言

蒸散是流域水量循环的重要环节[1]。受气候条件和下垫面状况等诸多因素的影响，流域尺度上的实际蒸散很难直接通过观测手段得到[2]。在流域水文资料稀缺或模拟时间序列较短的条件下，采用水量平衡法准确模拟流域实际蒸散时可能面临挑战。Penman于1956年提出了“正比假设”，假设实际蒸散与蒸发能力成正比[3]。Bouchet于1963年提出了“互补理论”，假设蒸发能力与实际蒸散成互补关系[4]。由于互补理论未将下垫面条件引入模型，因此不能反映下垫面条件对实际蒸散的定量化影响[5]。为此，Budyko在考虑下垫面的情况下提出了建立流域水量与能量耦合平衡方程的构想，即Budyko假设[6]。1981年我国学者傅抱璞基于该假设，通过量纲分析和数学推导得出了Budyko假设的解析表达式[7]。孙福宝等通过对黄河流域内年降水、径流及实际蒸散和蒸发能力的分析，证实了在黄河流域Budyko假设是成立的，并发现傅抱璞模型中反映流域下垫面条件的参数ω具有显著的区域分布规律[8]。韩松俊等使用傅抱璞模型模拟了塔里木盆地绿洲的年实际蒸散，发现模型参数ω与土地利用类型有关[9]。Donohue等认为有必要在Budyko假设中引入土地利用数据[10]。Yang等分析了多个干旱流域的水热平衡，发现降水是这些流域实际蒸散的主要气候影响因素[11]。岷江上游流域是成都平原重要的水资源来源，并且在西南流域具有代表性。本文基于傅抱璞模型估算岷江上游流域实际蒸散，评价该方法在流域的适用性，并分析其变化趋势和气候影响因子。研究对岷江上游流域水资源的科学管理具有积极意义，对该模型在西南流域其他区域的使用也有借鉴意义。

1 研究区概况及数据资料

岷江上游流域位于102°59′～104°14′E，31°26′～33°16′N，流域面积2.26万km2，包括四川省阿坝藏族羌族自治州的汶川县、理县、茂县、黑水和松潘五县。流域内部海拔高程为740～6 190 m，平均海拔3 440 m，属高原气候区，年平均气温5～12 ℃；年平均降水500～850 mm，其中5-10月降水占全年的80%[12,13]。

采用1980-2003年岷江上游流域及周边地区7个气象站(图1)的逐日气象数据，包括最高气温(Tmax)、最低气温(Tmin)、平均气温(T)、日照时数(n)、平均相对湿度(RH)、10 m风速(u10)和大气压强(P)。逐日降雨量数据来自流域的8个雨量站，逐月径流数据采用流域出口处的紫坪铺水文站，位置如图1所示。

图1 岷江上游流域位置图Fig.1 Location of runoff gauge, rainfall and meteorological stations in the study area

2 研究方法

2.1 傅抱璞公式

在年时间尺度上，流域蒸散同时受水分供应条件(降水量)和能量供应条件(蒸发能力)两个因素控制[8]。Budyko[6,15]假设随着气候越来越干燥，流域多年平均实际蒸散量逐渐趋近于多年平均降雨量。傅抱璞[7]在Budyko假设的基础上给出了一组微分关系：实际蒸散E随降水P的变化率∂E/∂P是剩余蒸发力E0-E和降水P的函数；实际蒸散E随蒸发能力E0的变化率∂E/∂E0是P-E和蒸发能力E0的函数。并通过量纲分析和微分方程理论得到了根据蒸发能力和降水计算陆面蒸发的解析表达式：

(1)

式中：E是实际蒸散量，mm；E0是潜在蒸散量，mm；P是降水量，mm；ω是无量纲的积分常数，反映下垫面条件(地形土壤植被等)调蓄作用，取值范围为(1，∞)[10]。本文采用傅抱璞模型计算岷江上游流域实际蒸散。

2.2 潜在蒸散的计算

采用1998年世界粮农组织(FAO)提出的修正Penman-Monteith方程计算潜在蒸散[15]：

(2)

式中：Δ是饱和水汽压曲线的斜率，kPa/℃；γ是干湿计常数，kPa/℃；Rn是地面净辐射，MJ/(m2·d)；G为土壤热通量，MJ/(m2·d)；u2为2 m高处风速，m/s；es和ea分别为饱和水汽压和实际水汽压，kPa。

地面净辐射为太阳净短波辐射和地面净长波辐射之差，其中太阳辐射的计算采用经验公式：

(3)

式中：Rs为太阳(短波)辐射，MJ/(m2·d)；Ra为太阳总辐射，MJ/(m2·d)；n和N分别为日照时数和最大日照时数，h；as和bs为代表地域气候特征的参数。根据Liu et al的研究[16]，对于岷江上游流域，as和bs分别取0.14和0.60。

使用流域内外7个气象站点数据计算各站点潜在蒸散，并用反距离权重插值得到研究区内潜在蒸散的平均值。

2.3 水量平衡法

水量平衡法是目前计算流域实际蒸散较为可靠的方法，常被用来评价其他模型的计算精度[11]。本文用水量平衡法计算的年实际蒸散评价傅抱璞模型的计算精度：

P=E+R+ΔW

(4)

式中：P为流域年降水量，由8个雨量站的数据采用反距离权重插值得到研究区降雨量平均值，mm；E为流域年实际蒸散，mm；R为紫坪铺水文站实测年径流量，mm；ΔW为流域蓄水量的年变化量，mm。

对于年尺度，流域蓄水量的变化可近似忽略。因此，流域年实际蒸散可由下式计算：

E=P-R

(5)

2.4 模型识别与验证

本文通过试错法率定傅抱璞模型中的参数ω，并采用逐年的相对误差(Re)和均方根误差(RMSE)检验计算精度，计算公式如下：

Rei=(Ef,i-Ewb,i)/Ewb,i

(7)

式中：n为时间序列长度；Ef,i和Ewb,i分别为第i年傅抱璞模型和水量平衡法计算的年实际蒸散。

通过调整ω，使RE和RMSE最小。本文将整个研究时段分为两阶段，1980-1995年的数据用来识别傅抱璞模型中的参数，1996-2003年的数据用来验证参数。

2.5 蒸散年际变化趋势检验

应用世界气象组织推荐并已广泛使用的非参数检验方法：Mann-Kendall检验方法分析岷江上游流域年实际蒸散的变化趋势。在检验中，原假设H0为时间序列数据(x1，…，xn)，是n个独立的、随机变量同分布的样本；备择假设H1是双边检验，对于所有的k，j≤n，且k≠j，xk和xj的分布是不相同的，检验的统计变量S计算如下式：

S=∑n-1k=1∑nj=k+1sgn(xj-xk)

(9)

式中：方差Var(S) =n(n-1)(2n+5)/18。当n>10时，标准正态统计变量计算如下：

(10)

双边的趋势检验中，在给定α置信水平上，如果|Z|≥Z1-α/2则原假设是不可接受的，即在α置信水平上，时间序列数据存在明显的上升或下降趋势。对于统计变量Z，大于0时，是上升趋势；小于0时，则是下降趋势。Z的绝对值在大于等于1.64时，表示通过了置信度95%的显著性检验。

2.6 敏感性分析

采用灵敏度法分析模型模拟的实际蒸散对主要气候影响因子的敏感性。灵敏度是指当蒸散模型中某一气象变量发生变化时，实际蒸散输出结果大小发生变化的程度[17]。计算公式如下：

(11)

式中：Sx为灵敏度；Xi为模型中某一参数；Sx值越大表明实际蒸散对该气候因子变化越敏感。

3 结果与讨论

3.1 模型率定结果

使用试错法最终确定ω值为1.50。水量平衡法与参数率定后的傅抱璞模型计算的多年实际蒸散结果如图2所示。结果表明，两者变化趋势基本一致。尽管傅抱璞模型计算的年实际蒸散波动幅度较小，但总体来说模拟精度较高。误差统计值如表1所示，在识别期(1980-1995年)用水量平衡法确定的多年平均实际蒸散为307.1 mm，傅抱璞模型模拟结果的相对误

表1 傅抱璞模型年实际蒸散模拟结果统计Tab.1 Statistics of the annual ET of Fu Baopu model

差Re为-0.08%；在验证期(1996-2003年)用水量平衡法确定的多年平均实际蒸散为294.4 mm，傅抱璞模型模拟结果的相对误差Re为-1.41%。从图3可以看出，当ω值偏离1.50时，RE和RMSE的绝对值均呈上升趋势，因此岷江上游流域最优ω值确定为1.50。

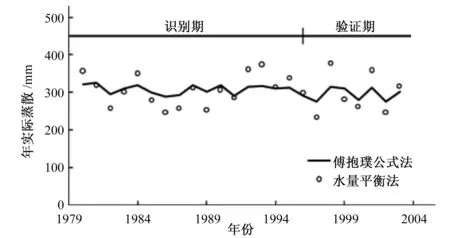
图2 识别期与验证期年实际蒸散模拟结果Fig.2 The simulated annual ET during calibration and validation periods

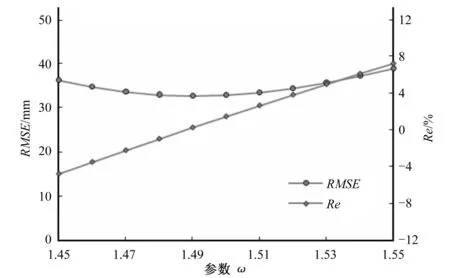
图3 RE、RMSE与ω值的关系Fig.3 Variations of RE and RMSE with ω

3.2 实际蒸散在年和季节尺度上的变化特征

本文采用参数率定后的傅抱璞模型分析实际蒸散在年和季节尺度上的变化特征。图4为1980-2003年傅抱璞模型计算的岷江上游流域多年实际蒸散。研究区多年实际蒸散均值为304.6 mm。年实际蒸散最大值出现在1981年，为321.5 mm；最小值出现在1997年，为273.3 mm。Mann-Kendall检验表明岷江上游流域年实际蒸散呈显著下降趋势(通过95%信度检验)，下降速率为-7.8 mm/(10 a)。

季节尺度上，夏季(6-8月)多年平均蒸散最高，为107.9 mm；春季(3-5月)次之，为93.2 mm；秋季(9-11月)和冬季(12-2月)较小，分别为61.1和42.2 mm。四季都呈现下降趋势，其中春、夏两季通过了置信度为95%的显著性检验。春、夏、秋、冬的下降幅度分别为-3.1、-2.2、-1.3和-1.3 mm/(10 a)，见图5。

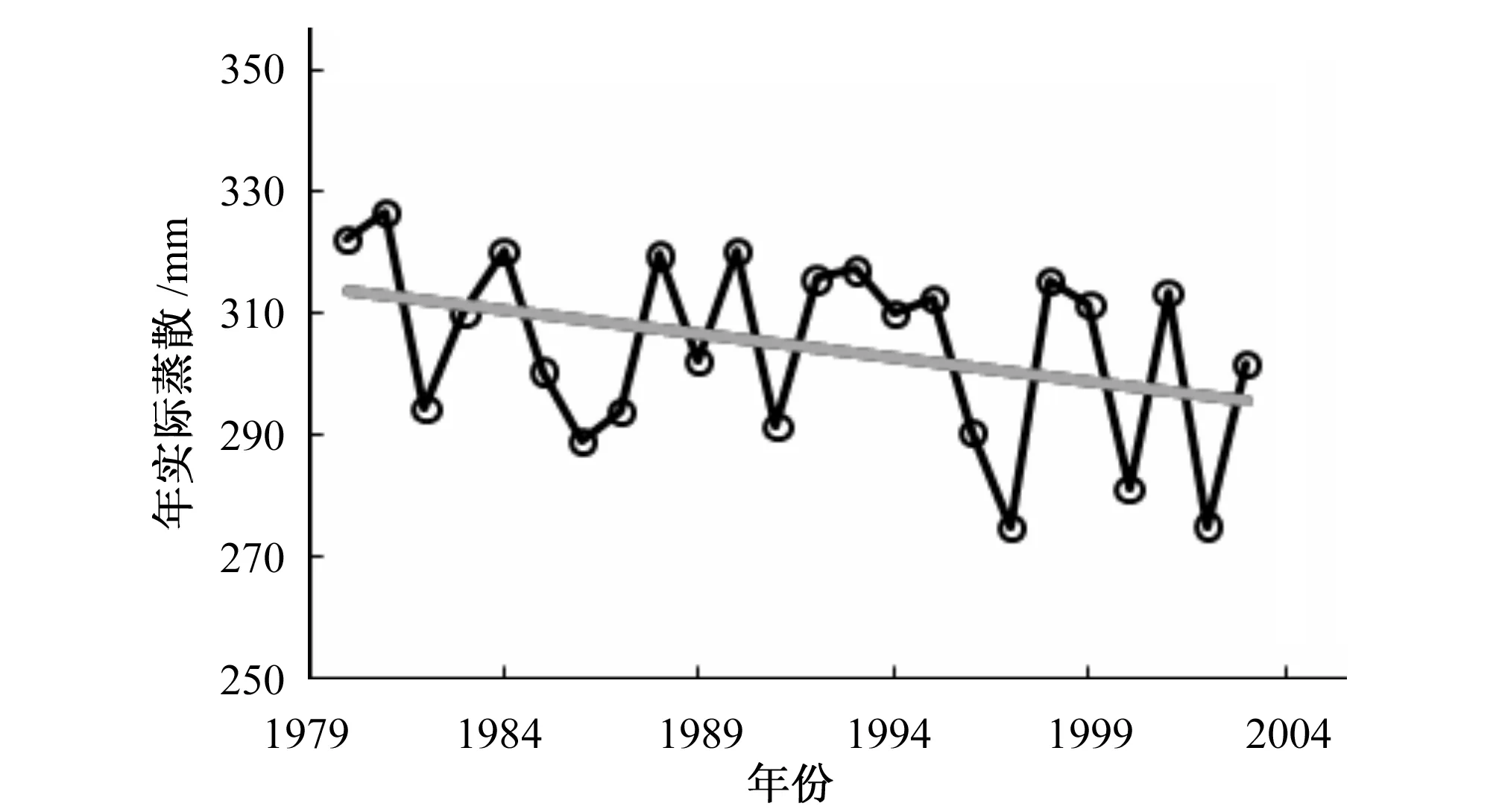
图4 多年实际蒸散年际变化Fig.4 Variations of actual annual ET

图5 多年实际蒸散季节变化Fig. 5 Seasonal variations of actual ET

3.3 岷江上游流域实际蒸散的气候影响因素

傅抱璞模型中计算实际蒸散的变量包括降雨量和潜在蒸散。潜在蒸散用Penman-Monteith公式计算，涉及的气象变量包括风速、气温、相对湿度和日照时数。本文用参数率定后的傅抱璞模型；结合公式(11)，确定年实际蒸散对降雨、风速、平均气温、日照时数和相对湿度变化的敏感度，并确定岷江上游流域年实际蒸散的主要气候影响因素。结果如表2所示，年实际蒸散对年降雨量最为敏感，灵敏度达到了0.102；之后依次为相对湿度、日照时数、风速和平均气温。因此降雨量是岷江上游流域年实际蒸散的主要气候影响因子。降雨量和相对湿度反映了流域的水分条件，而日照时数在一定程度上反映了太阳辐射对流域蒸散提供的能量条件。

表2 气候因子灵敏度列表Tab.2 Sensitivity of climate factor

3.4 模拟误差分析

利用傅抱璞模型模拟实际蒸散时可能存在一定误差。我们认为，造成模拟误差的原因可能有两方面：一是在利用水量平衡法计算结果率定参数的过程中，忽略了流域蓄水量(如水利工程的蓄排水量、丰枯水年水量)的变化。根据作者调查，岷江上游流域大型水利工程大多建设于20世纪90年代后期[18]。因此，水量平衡法的结果在识别期(1980-1995年)的误差较小；在验证期(1996-2003年)存在误差增加的情况。而丰枯水年蓄水量的年际差异会带来一定的不确定性。另一方面，由于研究区内有长期观测资料的气象站比较稀缺，气象数据较难获取，部分气象数据使用了周边站点的气象资料，并采用反距离权重插值方法确定流域内潜在蒸散和降雨量平均值。由此也带来一定的不确定性。

4 结 论

(1)利用傅抱璞模型模拟1980-2003年岷江上游流域的实际蒸散。对于研究区，通过试错法确定傅抱璞模型中的参数ω为1.50。结果表明，傅抱璞模型在岷江上游流域对实际蒸散有较好的模拟精度。

(2)Mann-Kendall检验表明岷江上游流域年实际蒸散呈显著下降趋势(95%信度)，且下降速率为-0.78 mm/a。研究区多年实际蒸散在四季都呈现下降趋势，其中春、夏两季呈现显著下降趋势(95%信度)。

(3)通过敏感性分析表明，影响岷江上游流域实际蒸散的主要气候因子是降雨量，其次是相对湿度和日照时数。

□

[1] 郭生练, 程肇芳. 平原水网区陆面蒸发的计算[J]. 水利学报, 1992,(10):68-72.

[2] 冯 雪, 蔡研聪. 浑太流域实际蒸散的时空变化特征及影响因素[J]. 应用生态学报, 2014,(10):2 765-2 771.

[3] Penman H L. Evaporation: an introductory survey [J]. Netherland Journal Agricultural Science, 1956,(4):9-29.

[4] Bouchet R. Evapotranspiration reelle at potentielle, signification climatique [J]. IAHS Publication, 1963,62:134-142.

[5] 李修仓. 中国典型流域实际蒸散发的时空变异研究[D]. 南京：南京信息工程大学, 2013.

[6] Budyko M I. Climate and Life[M]. Academic, San Diego, Calif, 1974.

[7] 傅抱璞. 论陆面蒸发的计算[J]. 大气科学, 1981,5(1):23-31.

[8] 孙福宝,杨大文. 基于Budyko假设的黄河流域水热耦合平衡规律研究[J]. 水利学报, 2007,38(4):409-416.

[9] 韩松俊, 胡和平, 田富强. 基于水热耦合平衡的塔里木盆地绿洲的年蒸散发[J]. 清华大学学报: 自然科学版, 2008,48(12):2 070-2 073.

[10] Donohue, RJ, Roderick ML, Mcvicar TR. On the importance of including vegetation dynamics in Budyko's hydrological model [J]. Hydrology and Earth System Sciences, 2007,11(2):983-995.

[11] Yang D, Sun F, Liu Z, et al. Interpreting the complementary relationship in non-humid environments based on the Budyko and Penman hypotheses [J].Geophysical Research Letters, 2006,33(18):L18402, doi:10.1029/2006GL027657.

[12] 曾 超,赵景峰,李旭娇.GIS支持下岷江上游水文特征空间分析[J].水土保持研究,2011,18(3):5-9,14.

[13] 樊 宏, 张建平. 岷江上游半干旱河谷土地利用/土地覆盖研究[J].中国沙漠, 2002,22(3):273-278.

[14] Budyko MI. The heat balance of the earth surface [M]. Washington: U.S. Dept of Commerce, 1958.

[15] Allen R, Pereira L, Raes D, et al. Crop evapotranspiration guidelines for computing crop water requirements[M]. FAO Irrigation and Drainage Paper 56. Food and Agriculture Organization of the United Nations, 1998.

[16] Liu CM. Spatial and temporal change in the potential evapotranspiration sensitivity to meteorological factors in China (1960-2007) [J]. Geogr. Sci, 2012,22(1):3-14.

[17] Li F, Lyons TJ. Estimation of regional evapotranspiration through remote sensing[J]. Journal of Applied Meteorology, 1999,38(11):1 644-1 654.

[18] 马怀新.四川水电史略[M].成都：四川科学技术出版社，2011.