面平均雨量误差和产流量误差修正的对比研究
——以富江流域为例
司 伟,余鸿慧,包为民,瞿思敏,张 乾
(1. 河海大学水文及水资源学院,南京 210098;2. 囯网新源水电有限公司富春江水力发电厂,杭州 311504)
降雨径流过程涉及蒸发、下渗、产流和汇流等多个环节,影响因素复杂,实时洪水预报精度难以满足要求。预报模型初始状态值误差、模型输入误差、模型结构的不充分性以及参数非优化都会影响预报结果的精度[1,2]。所以经常使用误差修正技术来减少模型在预报时产生的误差[3]。
简单的误差修正方法是通过流量误差直接对模型计算结果(流量过程)进行修正[4]。组合卡尔曼滤波(EnKF)或者粒子滤波(PF)方法经常通过数据同化技术对于模型初始值或者模型参数进行修正,然而研究结果表明滤波方法在预报修正中的效果过于自信,对于模型预报的不确定性估计不足[5]。
鉴于此,包为民等[6]应用系统响应理论,首次将单位线作为线性时不变系统,引入实时洪水预报修正中,建立了一种向信息源头追溯的反馈修正模型,该方法结构简单,物理概念清晰。之后司伟等[7]将动态系统响应曲线引入误差修正中,提出了产流误差动态系统响应曲线(Dynamic System Response Curve, DSRC) 修正方法,基于系统和微分角度,逐时段对产流量进行修正,该方法具有物理基础且不损失预见期,通过不同流域的应用检验[8,9],效果显著,明显优于传统的自回归修正方法。在随后的研究中,张小琴、刘可新等对此方法进行了改进[10,11],杨姗姗等将此理论方法引入对面平均雨量误差的修正研究中,通过修正水文模型的重要输入项(面平均雨量)误差,来提高水文模型的洪水预报精度,研究结果表明此方法对于雨量站密度较低的流域具有显著的效果[12]。
以上基于系统响应理论的洪水预报误差修正研究主要分为对面平均雨量误差进行修正和对产流量误差进行修正,两种方法对于提高洪水预报精度均有一定效果。然而,以上研究并未对两种方法在同一流域的应用效果进行探讨,鉴于此,本文作者将分别对两种修正方法进行简单描述,并对两种方法应用于富春江流域的结果进行对比和分析,希望对于研究人员选取合适的修正方法有一定的指导意义。
1 修正方法介绍
本文中两种修正方法(面平均雨量误差修正和产流量误差修正)均基于水文模型的系统响应理论,即将水文模型概化为输入与输出之间的响应系统,根据修正内容的不同来改变响应系统的结构。
1.1 面平均雨量误差修正方法
如图1所示,将水文模型作为一般系统考虑,图中P(t)为面平均降雨系列,E(t)为蒸散发,Q(t)为计算的流量过程,θ为模型参数,X(t)是模型状态变量,X0为状态初始值。图1中的水文模型系统可以表达为由输入、输出、参数和状态变量组成的系统方程:
Q(t)=f[P(t),E(t),X(t),θ]
(1)
式中:Q=[q1,q2,q3,…,qn]T为流域出口断面流量过程;P=[p1,p2,p3,…,pm]T为面平均雨量向量;E=[e1,e2,e3,…,en]T为蒸发;X=[x1,x2,x3,…,xn]T为状态变量向量;θ为参数向量。
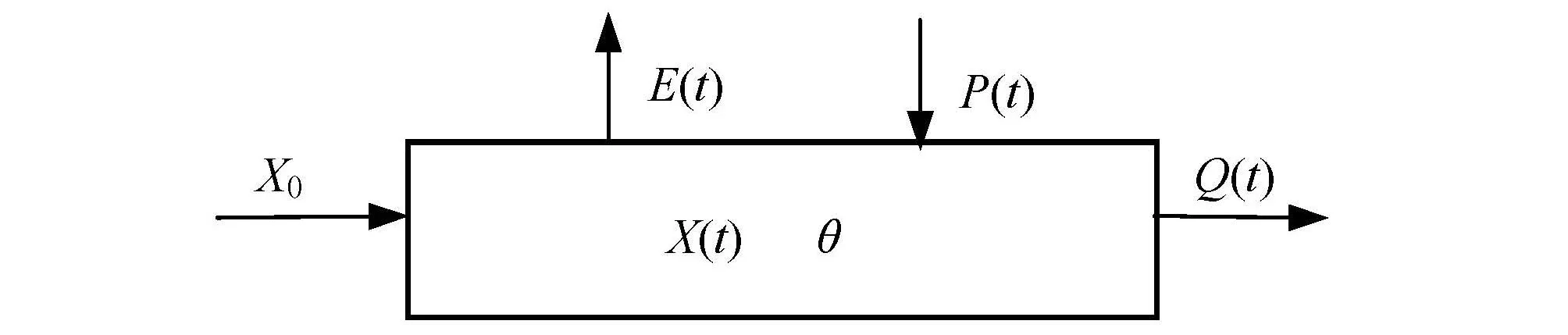
图1 一般水文模型系统示意图Fig.1 A systems diagram of general hydrological model
概念性模型的绝大多数参数都具有明确的物理意义,是流域水文特征的反应,模型参数一旦率定之后一般在短期之内不会改变。模型状态变量取决于模型的输入输出项[13],因此,此方法研究中认为模型参数不变化,面平均雨量的变化是引起流域出口断面流量变化的主要因素。上述系统方程可以简化为:
Q(P)=f(P)
(2)
对于流域水文模型,把降雨输入作为自变量求全微分,可得到式(2)的微分关系:
(3)
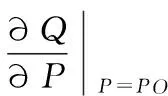
(4)
式中:Q(PO)为由降雨系列PO计算得到的流量系列。假设使用观测流量系列长度为L,Q(t)=[Q1,Q2,Q3,…,QL]T。代入式(4)可得:
(5)
则式(5)的矩阵形式为:
Q(P)=Q(PO)+SΔP+W
(6)
式中:ΔP=[Δp1,Δp2,Δp3,…,Δpm]T即为面平均雨量误差的估计值;W=[w1,w2,w3,…,wL]T为流量观测随机误差项,一般为服从零均值分布的为白噪声向量;S为系统响应矩阵,其表达式如(7)所示:
(7)
将式(7)代入(3)得到由降雨变化量与流量变化量表达的系统响应关系:
dQ=SdP
(8)
上式S矩阵中的每一项都可以用下式差分近似求解。
(9)
式中:Q(p1,…,pi,…)为由修正前的面平均雨量系列计算得到的流量系列;Q(p1,…,pi+Δpi,…)为由面平均雨量系列增加ΔPi之后计算得到的流量系列。
上式中当i不变,而j从1到L变化时,这L项差分值就是S矩阵中的一列。而此列正是雨量pi的单位变化量所对应的系统响应系列,本研究中称之为雨量pi所对应的系统响应曲线,S矩阵中的每一列均用同样方法求得。
对于一场洪水,假如有m个时段雨量,其相应的雨量误差依时间顺序为eP1,eP2,…,ePm,假如有L个时段的流量系列,流量的误差序列为eQ1,eQ2,…,eQL,则降雨误差与流量误差之间的关系可以表达为式(10):
(10)
上式表达为向量矩阵形式为:
EQ=S·EP
(11)
式(11)表达了降雨误差与流量计算误差的响应关系。则面平均雨量误差与流量误差之间的系统响应关系为:
EQ=S·EP+ζ
(12)
面平均雨量误差的最小二乘估计值为:
E′P=(STS)-1STEQ
(13)
式中:ζ为残差向量;E′P为降雨误差的动态系统响应曲线估计向量。由式(13)计算得到的面平均雨量误差系列加上原来的面平均雨量系列重新使用预报模型计算,便可得到通过降雨系统响应曲线反馈修正以后的流域出口断面流量过程。
1.2 产流量误差修正方法
此修正方法将预报模型的汇流部分作为响应系统,如图2中虚线框内系统,通过计算时段产流量所对应的系统响应曲线来修正产流量,进而修正出口断面流量过程。图2中方框内SERM表示蓄满产流,TLSE表示三层蒸散发,SORC表示分水源,FC表示汇流,MMSSR表示马斯京根河道分断连续演算。E为蒸散发,P为降雨,R为产流量,RS、RI和RG分别为划分以后的3种径流成分,Q为坡地汇流后的流量,QT为流域出口的总径流过程。

图2 新安江模型概化系统示意图Fig.2 The generalized system diagram of XAJ model
则产流量和模型预报流量之间的系统响应函数可以表示为:
Q(t)=Q(R,θ,t)
(14)
与面平均雨量误差修正方法类似,由式(13)可得到产流量的修正量的计算式为:
ΔR=(UTU)-1UT[Q(R,θ,t)-Q(RC,θ,t)]
(15)
式中:U为产流量系统响应矩阵;RC为修正前计算产流量系统,则修正后的产流量系列为:
R′C=RC+ΔR
由式(16)计算出修正后的产流量R′C。 将修正后的产流量系列重新用新安江模型进行计算,即可得到修正的流域出口断面的计算流量过程QU。
2 应用对比
2.1 流域介绍
富春江流域面积为18 866 km2,流域内共有28个雨量站,多年平均降雨量为1 659.2 mm。其中兰溪水文站是富春江干流上的重要入库控制站,控制总流域面积的85%,控制范围内有24个雨量站,对于整个流域的洪水控制和管理起着重要作用。富春江水库为调节能力较小的日调节水库,承担着防洪灌溉、发电、城市供水、航运以及平衡下游河道水环境容量和应对突发水质事件等重要功能,因此入库洪水预报的精度非常重要。富春江水库上游的两个重要支流分别是金华江和衢江,两条主要支流上均有径流式电站,其放水流量不规律,尤其是衢江小溪滩径流式电站以上还有大型水库,流域内的水利工程设施给富春江水库的入库洪水预报造成很大的困难。由于富春江流域面积较大,而流域内雨量站个数相对较少,雨量站密度较低(673.8 km2/个),造成雨量站资料代表性不足。对于空间集总式或半分布式水文模型,流域的大小以及流域内雨量站密度会对面平均雨量计算有较大影响。
2.2 应用结果对比
鉴于富春江流域洪水预报误差的两个主要方面的影响,本文将两种不同的预报误差修正方法应用于富春江流域,并对应用结果进行对比分析。本文使用富春江流域2010-2014年间的14场历史洪水进行了验证。两种方法修正后的计算结果如表1所示。
由表1的数据可知,经过两种方法的应用14场历史洪水的预报精度均有明显提高。在面平均雨量误差修正方法中,平均NS系数由修正前的0.769提高到0.848,提高了0.079;径流深相对误平均值由修正前的-1.5%减小到-0.6%,减小了0.9%;洪峰相对误平均值由修正前的-1.1%减小到-0.3%,减小了0.8%;对于产流量误差修正方法,平均NS系数由修正前的0.769提高到0.853,提高了0.084;径流深相对误平均值由修正前的-1.5%减小到-0.6%,减小了0.9%;洪峰相对误平均值由修正前的-1.1%减小到-0.1%,减小了1.0%,结果显示两种修正方法均有明显的效果。
为了分析不同量级洪水修正效果的代表性,本文中将历史洪水分级。由表1可知,14场历史洪水的平均次洪降雨量为206.9 mm,故本文中将降雨量大于平均次洪雨量的历史洪水归为大洪水(1~5号洪水),其余归为中小洪水(6~14号洪水)。验证两种方法对于不同量级洪水修正效果提高的幅度,本文中使用如下指标:
δNS=(NS-M-NS-X)/(NS-C-NS-X)
(17)
式中:NS-M为面平均雨量修正方法的效果;NS-C为产流量修正方法的效果;NS-X为未经修正的新安江模型计算结果。其值大于1则表明面平均雨量误差的修正效果比产流量修正方法修正效果好,小于1则后者修正效果优于前者。修正效果对比如图3所示。
由图3结果可以看出,对于5场大洪水,面平均雨量修正方法的效果比产流量误差修正的效果好,由于富春江流域雨量站密度较低,降雨量较大时,采用雨量站单点雨量代替雨量站单元的面平均雨量进行预报时,由雨量代表性误差造成的预报误差更加明显和突出。对于中小洪水,产流量修正方法的效果比面平均雨量误差修正方法效果好,是因为次洪雨量小,由雨量误差引起的流量误差相对减小,而产流量误差中包含了其他方面误差,因此产流量修正方法对于中小洪水的修正效果较好。但是从修正效果的平均值来看,产流量误差修正方法的修正效果优于面平均雨量误差修正方法。
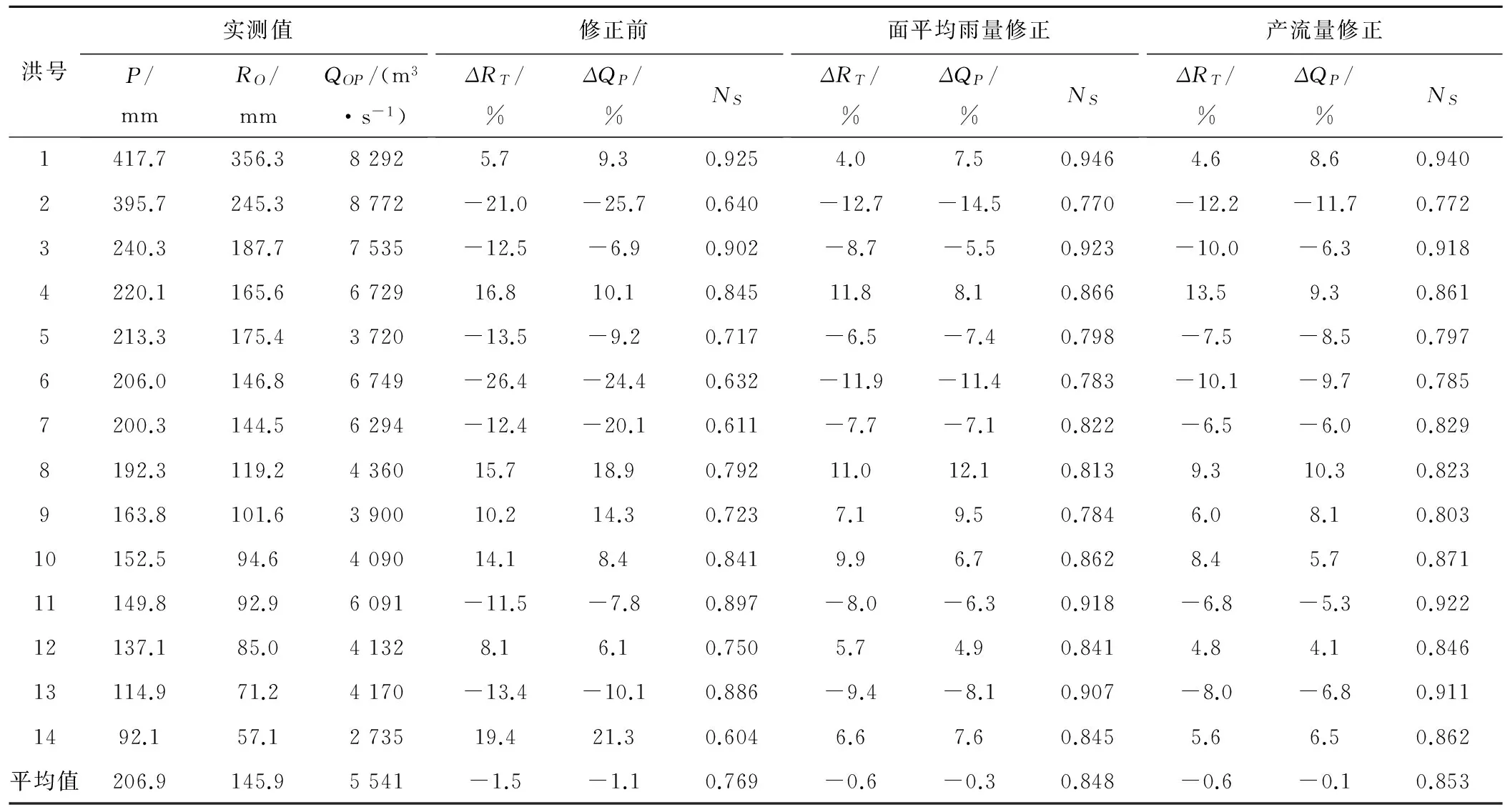
表1 富春江流域14场历史洪水的实测值和修正前后的结果对比Tab.1 The observed values, simulated results and updated results of the 14 flood events in Fuchunjiang basin
注:表中P表示降雨,RO表示实测径流深,QOP表示实测洪峰流量,ΔRT表示径流深相对误差,ΔQP表示洪峰流量相对误差,NS表示Nash-Sutcliffe系数。
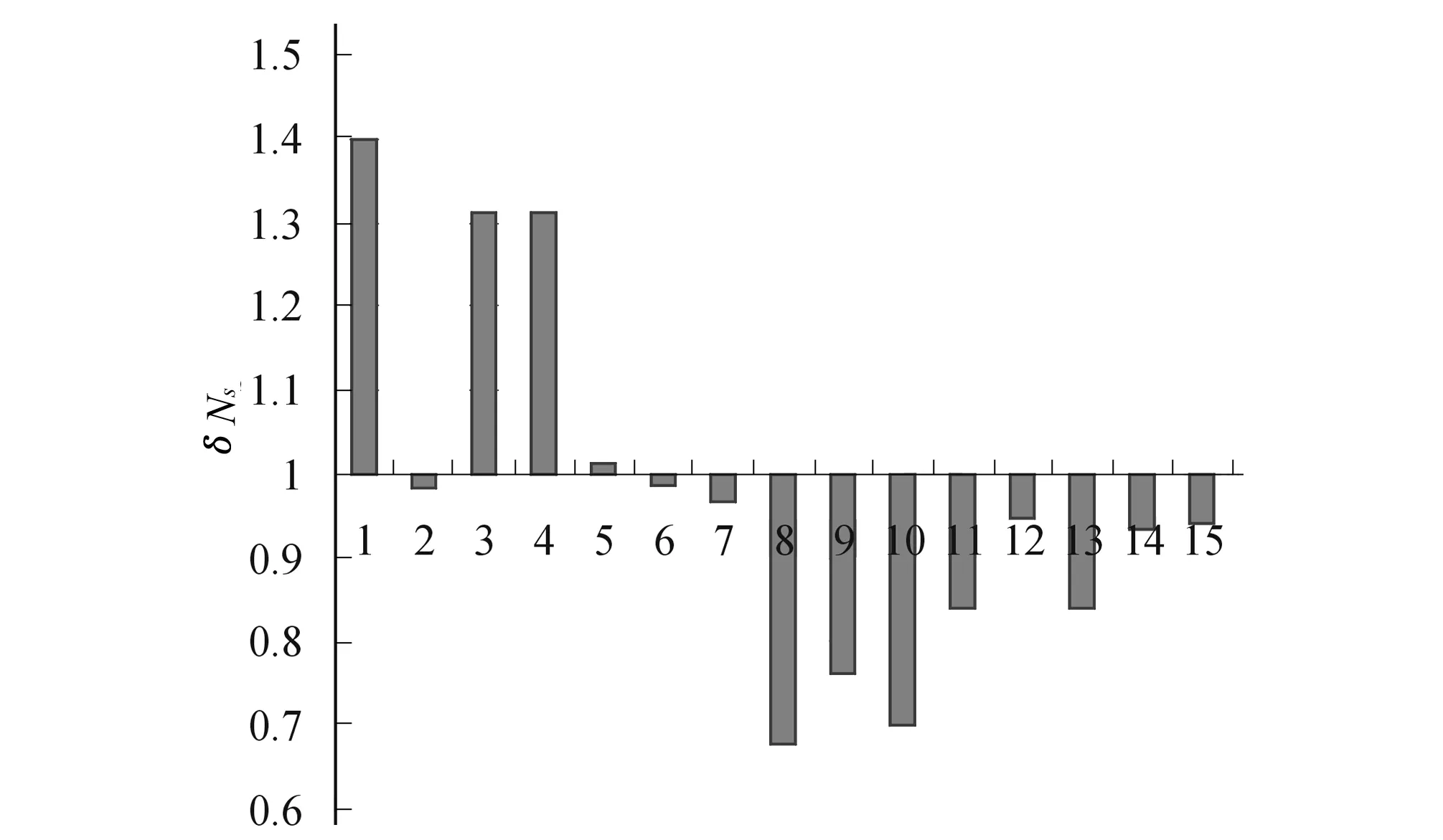
图3 两种方法修正效果对比Fig.3 Improvement comparison of the two updating method
3 结 语
本文将基于系统响应曲线的面平均雨量误差修正方法与产流量误差修正方法应用于富春江流域的相同历史洪水中,通过对应用结果的对比和分析,两种方法修正后的平均NS系数分别由修正前的0.769提高到0.848和0.853,分别提高了0.079 和0.084,均具有较为明显的修正效果。
然而通过不同量级洪水修正效果的对比得出,在对于大洪水进行修正应用时,面平均雨量修正方法的修正效果较好,对于中小洪水,产流量修正方法的效果优于面平均雨量方法的效果。另外,面平均雨量修正方法适用于所有概念性水文模型,因此在次洪降雨量较大且雨量站密度较低的大流域推荐使用面平均雨量修正方法。在应用于次洪降雨量较小的中小型流域时,尤其当使用的水文模型为集总式产流模型(如新安江模型、HYMOD等)时,建议使用产流量修正方法。希望本文的研究结果对于研究者选取适当的实时洪水预报误差修正方法具有一定的指导意义。
□
[1] Komma J, Bloschl G, Reszler C. Soil moisture updating by ensemble kalman filtering in real-time flood forecasting[J]. Journal of Hydrology, 2008,357(3-4): 228-242.
[2] Lee W L, Eugene L P. Accuracy of precipitation measurements for hydrologic modeling[J]. Water Resources Research, 1974,10(4):857-863.
[3] 瞿思敏, 包为民. 实时洪水预报综合修正方法初探[J]. 水科学进展, 2003,14(2):167-171.
[4] Marco F, Anna B, Silvia B, et al. Forecasting discharges at the downstream end of a river reach through two simple Muskingum based procedures[J]. Journal of Hydrology, 2011,399:335-352.
[5] Moradkhani H, Dechant C M, Sorooshin S. Evolution of ensemble data assimilation for uncertainty quantification using the particle filter-markov Chain monte carlo method[J]. Water Resources Research, 2012,48(12), W12520, DOI:10.1029/2012WR012144.
[6] 包为民, 司 伟, 沈国华, 等. 基于单位线反演的产流误差修正[J]. 水科学进展, 2012,23(3):315-322.
[7] Bao W, Si W, Qu S. Flow updating in real-time flood forecasting based on runoff correction by dynamic system response curve[J]. Journal of Hydrologic Engineering, 2014,(19):747-756.
[8] 刘可新, 包为民, 赖善证, 等. 动态系统响应曲线修正方法在乌溪沟流域的应用[J]. 中国农村水利水电, 2014,(12):24-6.
[9] 阙家骏, 包为民. 产流误差的动态系统响应曲线修正方法应用[J]. 三峡大学学报(自然科学版), 2014,36(6):6-9.
[10] 张小琴, 刘可新, 包为民, 等. 产流误差比例系数的系统响应修正方法[J]. 水科学进展, 2014,25(6):789-96.
[11] 刘可新, 包为民, 李佳佳, 等. 基于系统响应理论的分水源误差修正[J]. 水电能源科学, 2014,32(11):44-47.
[12] 杨姗姗, 包为民, 杨小强, 等. 微分响应在降雨误差修正中的应用[J]. 中国农村水利水电, 2015,(1):75-9.
[13] Hamid M, Soroosh S, Hoshin G, et al. Dual state-parameter estimation of hydrological models using ensemble Kalman filter[J]. Advances in Water Resources, 2005,28:135-147.

