一种改进的极限学习机煤与瓦斯突出预测模型*

付　华，李海霞，卢万杰，徐耀松，王雨虹（.辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛505；.辽宁工程技术大学机械工程学院，辽宁阜新3000）



一种改进的极限学习机煤与瓦斯突出预测模型*

付华1*，李海霞1，卢万杰2，徐耀松1，王雨虹1
（1.辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛125105；2.辽宁工程技术大学机械工程学院，辽宁阜新123000）

摘要：较高精度的煤与瓦斯突出预测是煤矿安全生产的必要前提和保证。为了提高煤与瓦斯突出预测模型的预测精度，提出了一种改进的极限学习机煤与瓦斯突出预测模型。首先利用核主成分分析法对煤与瓦斯突出的影响指标进行降维简化处理，提取指标数据的主成分序列；把主成分序列分为训练样本和验证样本，然后在训练阶段，使用训练样本通过结合了全局搜索和局部搜索的文化基因算法对极限学习机的输入权值和隐含层偏差进行优化，得到最佳预测模型；最后，在最佳预测模型中，用验证样本对煤与瓦斯突出强度进行预测。通过实例验证，该模型能够有效预测煤与瓦斯突出强度。与BP、SVM、ELM、KPCA-ELM等预测模型相比，该模型具有更高的预测精度。

关键词：煤与瓦斯突出；预测模型；极限学习机；核主成分分析法；文化基因算法

煤与瓦斯突出是煤矿井下一种及其复杂的动力现象［1］，是煤矿井下含瓦斯煤岩以粉碎状从煤岩层中向采掘空间急剧运动，并伴随有大量瓦斯喷出的一种强烈动力过程。我国是世界上煤与瓦斯突出最严重的国家之一［2-3］。随着矿井开采深度的不断增加，煤与瓦斯突出日益加剧，并且高地应力、高瓦斯压力更容易导致煤与瓦斯突出的发生［4-5］。因此，能够准确地预测煤与瓦斯突出，对煤矿安全生产有很重要的实际意义。

极限学习机ELM（Extreme Learning Machine）［6-7］是一种单隐层前馈神经网络SLFN（single-hidden layer feedforward network），其结构简单，具有极强的学习能力和泛化能力，能够逼近复杂的非线性函数，在模式识别、回归估计等领域得到了广泛的应用［8］。ELM是一种特殊的前馈神经网络，其输入层权值、隐含层权值和隐含层偏差均是随机产生的，输出层权值是通过计算获得的，在训练过程中不需要调整网络参数，只需设置隐含层神经元个数，即可获得唯一的全局最优解，很好地克服了传统神经网络存在的训练时间长、过拟合等问题。由于输入层权值是随机给定的，ELM具有输出波动大、模型不稳定等特点。因此，在设计ELM网络时，如何确定最优网络结构一直都是研究的重点。文献［9］通过遗传算法（GA）对ELM的输入权值和隐含层偏差进行优化，将GA与ELM相结合，得到了结构紧凑和预测精度高的网络模型。文献［9］的方法为ELM优化提供了很好的方向。

为了提高煤与瓦斯突出预测模型的预测精度，提出了一种核主成分分析法和改进的极限学习机（Memetic-ELM）相结合的预测模型。运用核主成分分析法KPCA（Kernel Principal Component Analysis）对影响煤与瓦斯突出的指标因素进行降维简化处理，提取指标因素的主成分序列；在极限学习机预测模型中引入结合了全局搜索和局部搜索的Memetic算法，优化极限学习机的网络参数——输入权值和隐含层偏差，同时用主成分序列的训练样本训练极限学习机网络，得到最佳预测模型；最后，结合验证样本数据，利用模型对煤与瓦斯突出强度进行预测。

1　煤与瓦斯突出预测指标的选取

煤与瓦斯突出是煤矿生产过程中常发生的严重自然灾害之一，严重影响煤矿的安全生产和技术经济指标，又对煤矿工作人员的人生安全造成巨大伤害。因此，能够准确预测煤与瓦斯突出是一件至关重要的事情。由于各个煤矿的大小、地理位置、开采情况等不同，煤与瓦斯突出的情况也是各不相同的。确定煤与瓦斯突出的预测指标，是准确预测煤与瓦斯突出的理论基础。

煤与瓦斯突出的影响因素较多且关系复杂，大多数人赞同煤与瓦斯突出是地应力、瓦斯和煤结构的物理学性质等多个因素综合作用的结果［10-11］。根据煤矿安全相关研究以及突出事故的历史数据，结合我国煤矿突出的特点，将影响煤与瓦斯突出的因素归纳为3大类：煤性质、瓦斯因素与地质因素，在这3大类指标下又分16个3级指标，如图1所示。在本文的预测模型中，将这16个指标构建为煤与瓦斯突出危险性评价指标体系。

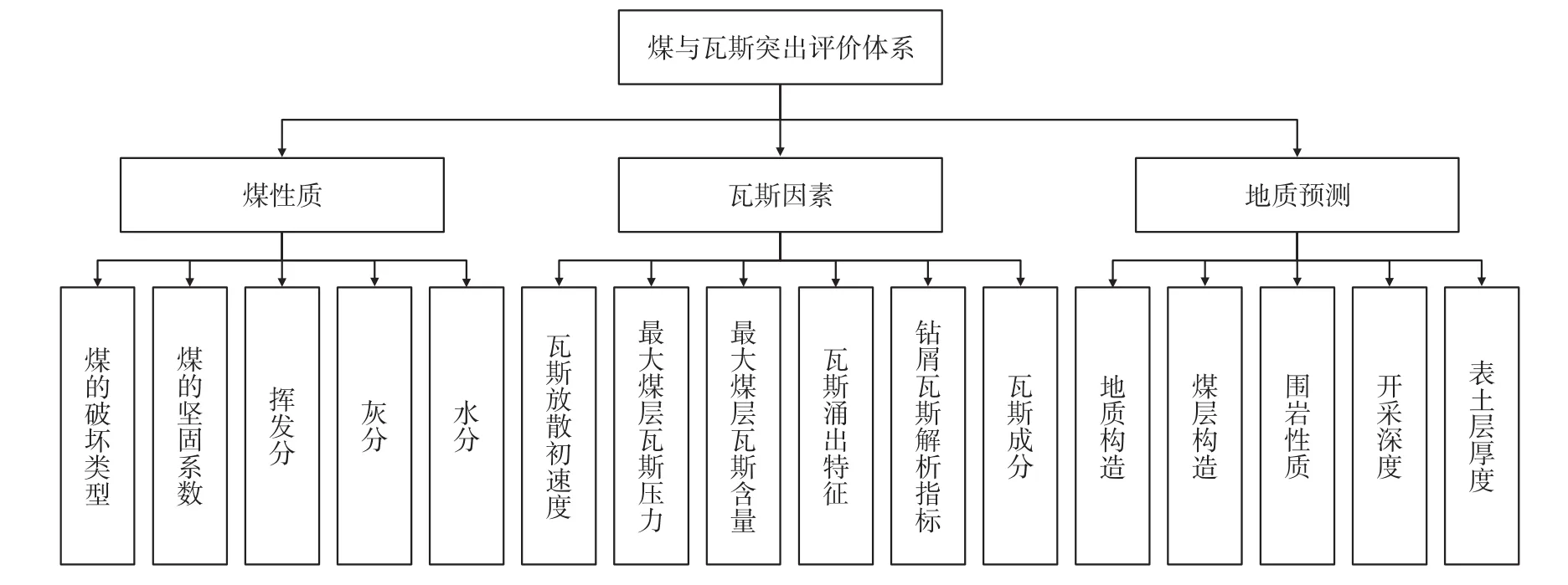
图1　危险性评价指标体系结构图

2　预测模型的建立

图1中的16个三级指标是针对全国各地的煤矿提出的，范围较广，针对性不强。由于各个煤矿的地理环境、开采情况、仪器设备等不同，从而各个指标占的比重有所不同，因此要选取最符合所预测矿井的指标进行建模。为了保证降低指标个数和提高模型的预测精度，选用KPCA对指标进行主成分分析，提取主要评价指标，减少数据冗余量和预测模型的训练时间；再将主要指标值带入ELM网络进行学习训练和预测，同时用Memetic算法优化ELM的网络参数——输入权值和隐含层偏差，得到最佳预测模型。

2.1基于KPCA的指标提取

近年来，随着对神经网络研究的深入，核方法的运用得到迅速的推广和重视。KPCA是将核函数融入到PCA中，是一种处理非线性问题的方法，其主要思想是通过非线性映射函数将输入矢量映射到一个高维特征空间，然后在特征空间中进行线性可分计算主成分［11-12］。

在影响煤与瓦斯突出的16个三级指标中，通过KPCA计算提取出占比重较大的几个三级指标。设为煤与瓦斯突出的一组指标向量，其中xi∈Rd，N为指标向量个数，d表示指标向量的维数。首先，在非线性空间中引入非线性映射ϕ，使输入空间中样本点x1，x2，…，xN变换为特征空间F中的样本点ϕ(x1)，ϕ(x2)，...，ϕ(xN)。其次，在特征空间中，引入核函数Ki.j。然后，在特征空间中求解特征空间上的特征值λ和特征向量ω，即可得到一组主成分指标。然后，计算各个主成分指标的贡献率，并把贡献率由大到小进行排列，第k个主成分的贡献率表示为，则累计贡献率为

若前m个主成分指标的累计贡献率超过一定值（一般取为80%~95%），则求得的主成分指标可以充分体现原16个指标中的数据信息。

2.2极限学习机预测模型

极限学习机是Guangbin Huang为了解决前馈神经网络学习速度缓慢的问题，进而提出的一种新的单隐层前馈神经网络。在建立的ELM煤与瓦斯突出预测模型中，设ELM的隐层节点有N个，训练样本集为(xi，ti)∈RN×RM，其中xi=[xi1，xi2，…，xiN]T，ti=[ti1，ti2，…，tiM]T，隐层激活函数为g(x)，则预测模型表示为：

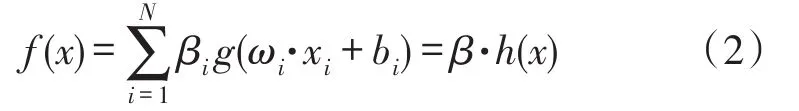
式中，ωi为网络输入神经元到第i个隐层节点的输入权值；bi为第i个隐含层节点的偏差；βi为第i个隐层节点到输出神经元的输出权值；h(x)为隐层输出权阵。可简化为

在模型训练过程中，ωi和bi是随机产生的，不需要调整，通过线性方程组Hβ=T求解其最小二乘解，即为对ELM网络进行训练，建立ELM预测模型。

式中，H+为隐层输出矩阵T的Moore-Penrose广义逆。

ELM随机产生输入层权值和隐含层偏差，通过计算求得输出权值，避免了在迭代过程中调整神经网络参数的繁琐；相对于传统的学习算法（如BP算法），其学习速度更快、泛化性能更强。因此，将ELM应用于煤与瓦斯突出预测中，能大大提高预测的精度和计算效率。

2.3Memetic算法对ELM模型参数的优化

由ELM的原理可知，ELM存在随机产生输入层权值和隐含层偏差的缺点，使得模型的泛化能力和稳定性不理想。因此，本文提出用Memetic算法对ELM模型参数寻优的一种方法。

Memetic算法［13-15］是一种基于种群的全局搜索和基于个体的局部搜索的混合算法，它结合了群体算法搜索范围大的优点和局部搜索算法的深度优势。该算法实质上是一种框架，在此框架下采用不同的搜索策略可以形成不同的文化基因算法。针对ELM的参数优化问题，本文采用浮点数编码的遗传算法进行全局搜索，用下山单纯法作为局部搜索策略。

运用Memetic算法优化ELM模型参数的优化，具体步骤如下：

Step 1求解煤与瓦斯突出预测寻优函数的可行解，使用二进制编码为搜索空间的浮点型串结构数据。

Step 2通过随机的方法生成煤与瓦斯突出模型初始群体解P。

Step 3对初始产生的M个个体，按照杂交概率任意选取两个进行杂交运算，产生新一代群体的两个新个体。

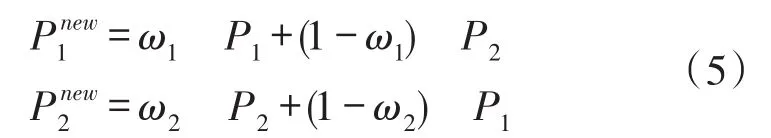
式中，P1和P2为种群中随机选择的两个父个体；为通过交叉运算子运算后产生的子代对应新个体；ω1、ω2为［0，1］上随机选取的参数。

Step 4在产生的新群体中，按照一定变异概率选取若干个体，按下式进行变异操作。

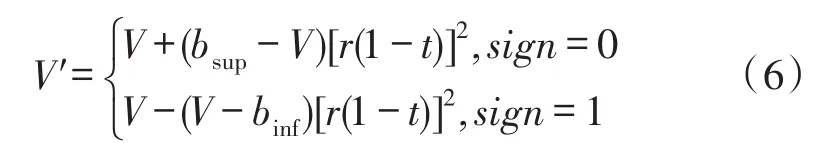
式中，V是选中的变异参数；V′为变异后的参数；sign随机取0或1；bsup和binf分别为参数取值的上界和下界；r为［0，1］上产生的随机数；t=gc/gm为种群进化标志，其中gc是种群的当前进化代数，gm是种群的最大进化代数。

Step 5计算每个染色体的适应度Ji=f(xi)。

Step 6按照一定选择概率从当前变异群体中选择M个适应度高的个体，使它们成为下一次迭代过程的新个体。每个个体的选择概率为：

Step 7采用MATLAB中自带的Fminsearch优化函数来实现对当前种群中的所有个体采用单纯法进行局部搜索。

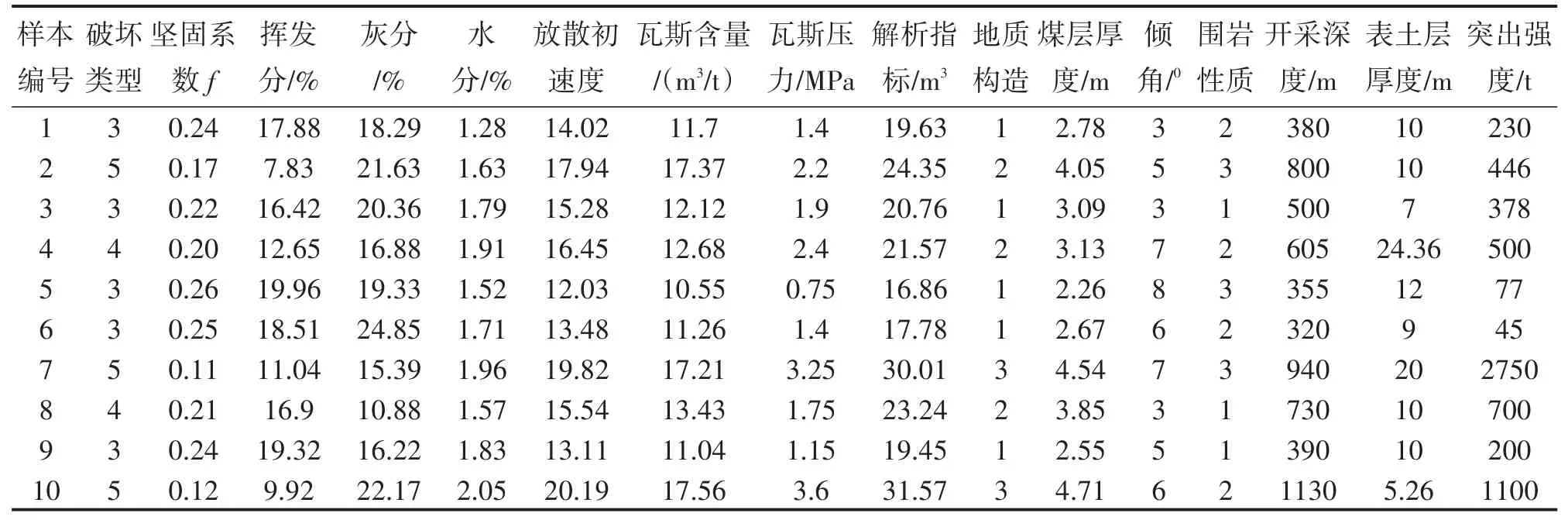
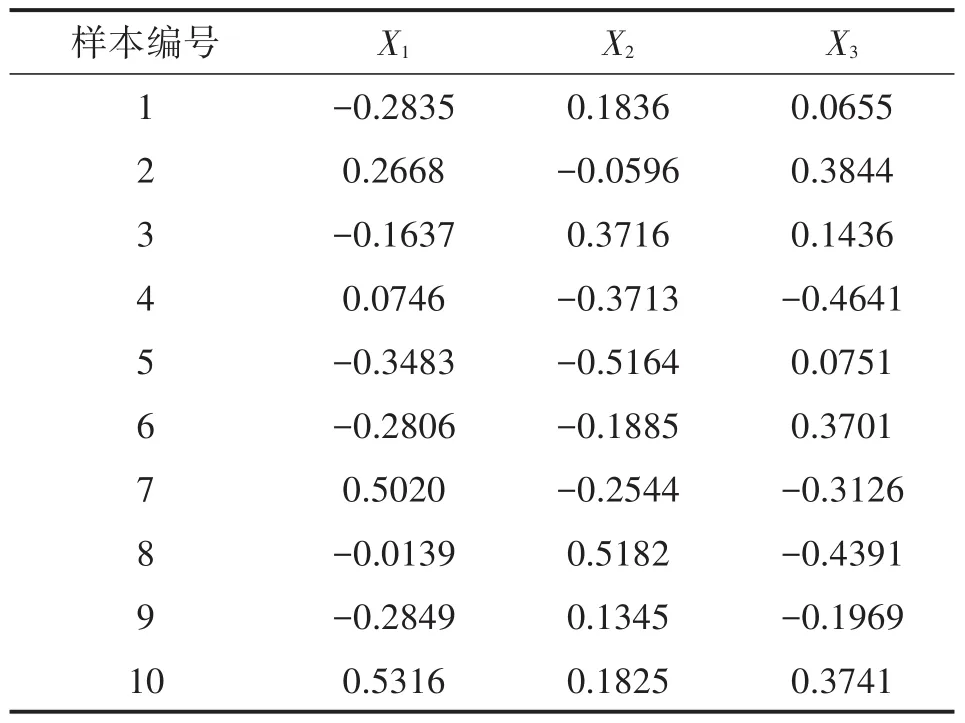
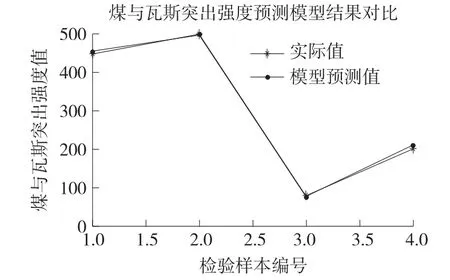
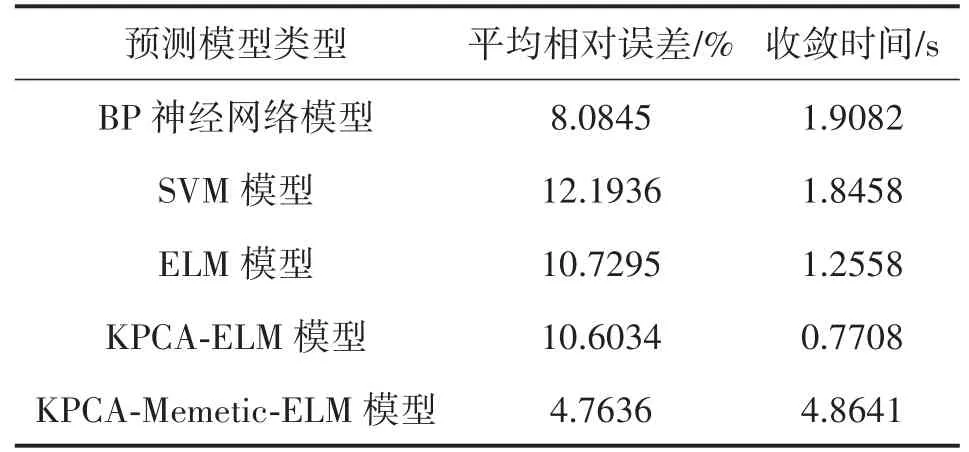
Step 8令进化代数gc=gc+1，如果gc

Step 9输出最优解，建立ELM预测模型。

3　实例分析

根据图1中的危险指标评价体系，选取某矿区的煤与瓦斯突出系统中的相关三级指标因素作为本预测模型的样本集，见表1所示。其中，由于瓦斯涌出特征指标是可解吸瓦斯含量和煤体性质的复合指标，瓦斯成分指标是指其中碳氢含量比例，这两个指标适用于纵向比对，因此本文不作考虑；根据煤的亮度、光泽、构造、节理性质以及断口、强度等特征，煤的破坏类型划分为5类，依次用1~5表示；煤层构造重点针对煤层厚度、倾角等煤层特征；根据围岩性质特征，粉砂岩记为1，砂质泥岩记为2，含砂最低的泥岩记为3。因此，适用于本煤矿的三级指标一共是15个。

表1　煤与瓦斯突出系统指标因素样本集

对样本集进行归一化预处理，然后通过KPCA提取15个三级指标中占主导地位的主成分因素。根据累计贡献率为0.85以上的主成分基本上包含了全部特征所具有的信息，将主成分贡献率由大到小排列，计算可得排列前三项的主成分累计贡献率达0.882 0，它们的贡献率分别为0.651 9、0.133 2、0.096 9。根据主成份选取标准，累计贡献率大于0.85的前3名三级指标完全可替代原来的15项三级指标。因此，选取前3个主成分作为建立ELM预测模型的新指标。以这3个新指标为基础，计算ELM网络的核矩阵在相对应的特征向量上的投影X1、X2、X3，即经过KPCA降维简化后得到的煤与瓦斯突出三级指标主成分数据，见表2。

采用Memetic算法对ELM预测模型参数进行优化，取得最佳预测模型。把样本数据分为两组：选取第2、4、5、9组数据作为检测样本，其余数据作为训练样本。建立一个三层神经网络结构的ELM预测模型，其中经过KPCA提取的三个新指标作为网络输入变量，煤与瓦斯突出强度作为网络输出变量。设置Memetic算法初始参数：变异概率为0.1，杂交概率为0.95，种群规模为10，最大迭代次数为100。在Memetic算法中以公式（3）为寻优函数开始寻优，通过迭代计算到大概20代左右便可找到全局最优的ELM模型输入权值和隐含层偏差，得到最佳预测模型。对优化的ELM模型进行煤与瓦斯突出预测验证，预测结果如图2所示。

表2　KPCA降维后的主成分因素

图2　预测模型的预测结果图

由图2可知，本文提出的一种改进的极限学习机煤与瓦斯突出预测模型的预测值逼近真实值，其预测准确性良好。为了更好地说明该模型的预测性能，通过与BP、SVM、ELM、KPCA-ELM网络预测模型进行对比，预测对比结果如表3所示。在对比中，BP神经网络模型根据文献［16］采用3层网络结构，15个输入节点，31个隐含层神经元，1个输出节点，激励函数为Sigmoid函数，学习率为0.01，训练次数为300次，预测结果的平均相对误差为8.084 5%，收敛时间为1.908 2 s；SVM模型根据文献［17］选用RBF核函数，采用GA对SVM网络参数进行寻优，选取的惩罚参数C=100、核参数σ=10，预测结果的平均相对误差为12.193 6%、收敛时间为1.845 8s；ELM模型和KPCA-ELM模型采用的是传统的ELM网络模型，其中隐层激活函数为Sigmoid函数，隐层节点数的搜索范围为［1，20］，寻到最优隐层节点数，预测结果的平均相对误差分别为10.729 5%、10.603 4%，收敛时间分别为1.255 8 s、0.770 8 s。

由表3可知，ELM模型的预测速度比BP神经网络模型、SVM模型的预测速度快很多；提出的预测方法比BP、SVM、ELM、KPCA-ELM模型的预测精度明显提高了；提出的预测方法引入了Memetic算法，其网络建模耗时相对较长。由于较高精度的煤与瓦斯突出预测是煤矿安全生产的必要前提和保证，在合理的预测时间范围内，更加注重预测模型的预测精度，因此，提出的预测模型比较适用于煤与瓦斯突出这类预测精度要求高的领域。

表3　预测模型预测结果对比

4　结论

①煤与瓦斯突出指标对准确预测煤与瓦斯突出强度有很重要的影响，利用核主成分分析法提取影响煤矿突出的主要指标，极大地提高了突出预测的训练速度。

②将Memetic算法和ELM网络相结合，引入到煤与瓦斯突出预测研究中，提出了一种改进的极限学习机煤与瓦斯突出预测模型，很好地提高了突出的预测精度。

③通过实例验证和与其它模型进行对比，该模型具有较好的预测功能，大大提高了煤与瓦斯突出预测的精度，适用于煤与瓦斯突出预测，对煤矿的安全生产和经济效益都有重要的意义。

参考文献：

[1]闺江伟，张小兵，张子敏.煤与瓦斯突出地质控制机理探讨［J］.煤炭学报，2013，38（7）：1174-1178.

[2]付华，王馨蕊，杨本臣，等.基于MPSO-CWLS-SVM的瓦斯涌出量预测［J］.传感技术学报，2014，27（11）：1568-1572.

[3]李成武，解北京，曹家琳，等.煤与瓦斯突出强度能量评价模型［J］.煤炭学报，2012，37（9）：1547-1552.

[4]崔鸿伟.煤巷掘进工作面突出预测指标及其临界值研究［J］.煤炭学报，2011，36（5）；808-811.

[5]刘雪莉，游继军.新型煤与瓦斯突出预测指标确定及应用［J］.煤炭科学技术，2015，43（3）；56-58.

[6] Huanu U B，Wand D H，Lan Y. Extreme Learning Machines：A Survey［J］. International Journal of Machine Learning and Cyber⁃netics，2011，2（2）：107-122.

[7] Huanu G B，Zhou H M，Dinu X J，et al. Extreme Learning Ma⁃chine for Regression and Multiclass Classification［J］. IEEE Transactions on Systems，Man，and Cybernetics，Part B：Cybernet⁃ics，2012，42（2）：513-529.

[8]张弦，王宏力.限定记忆极端学习机及其应用［J］.控制与决策，2012，27（8）：1206-1210.

[9]王辉，刘达，王继龙.基于谱聚类和优化极端学习机的超短期风速预测［J］.电网技术，2015，39（5）：1307-1314.

[10]关维娟，张国枢，赵志根，等.煤与瓦斯突出多指标综合辨识与实时预警研究［J］.采矿与安全工程学报，2013，30（6）：922-929.

[11]高宏宾，侯杰，李瑞光.基于核主成分分析的数据流降维研究［J］.计算机工程与应用，2013，49（11）：105-109.

[12]王雨虹，付华，张洋.基于KPCA和CIPSO-PNN的煤与瓦斯突出强度辨识模型［J］.传感技术学报，2015，28（2）：271-277.

[13] Liu Shixin，Chen Di，Wang Yifan. Memetic Algorithm for Multi-Mode Resource- Constrained Project Scheduling Problems［J］. Journal of Systems Engineering and Electronics，2014，25（4）：609-617.

[14] Zhou Jiarui，Zhu Zexuan，Ji Zhen. A Memetic Algorithm Based Feature Weighting for Metabolomics Data Classification［J］. Chi⁃nese Journal of Electronics，2014，23（4）：706-711.

[15]王洪峰，汪定伟，黄敏.动态环境中的Memetic算法［J］.控制理论与应用，2010，27（8）：1060-1068.

[16]曲方，张龙，李迎业，等.基于BP神经网络的煤与瓦斯突出预测系统开发［J］.中国安全科学学报，2012，22（1）：11-16.

[17]师旭超，韩阳.煤与瓦斯突出预测的支持向量机（SVM）模型［J］.中国安全科学学报，2009，19（7）：26-30.

付华（1962-），女，辽宁阜新人，教授，博士（后），博士生导师。主要从事智能检测和数据融合等方而的研究。主持国家自然基金2项、主持及参与国家863和省部级项目30余项，发表论文60余篇，申请专利24项，fxfuhua@163.com；

李海霞（1987-），女，四川蓬溪人，硕士研究生。专业：控制理论与控制工程，主要研究方向计算机测控技术与应用，m15541841065@163.com。

The Multi-Criteria On-Line Modeling and Filter for Random Error of MEMS Groscope*

DAI Jinhua1，ZHANG Lijie2*
（1.Inner Mongolia University of Technology College of Information Engineering，Hohhot 010051，China；2.Inner Mongolia University of Technology College of Electric Power，Hohhot 010051，China）

Abstract：As the random error of some MEMS gyroscope had weak correlation，the Multi-criteria curve method was introduced to identify the time-sequence model with a intercept. Using this model，the random error model of the MEMS gyroscope could be established on line without zero mean offline processing. Based on this model，an aug⁃menting state vector was used to design the Kalman filter which had been used to filter real-timely. The results of the experiment showed that AR（2）model with a intercept could be used as a good MEMS gyroscope random error model. After the on-line modeling and real-time filtering，50% of the standard deviation of the random error had been reduced and the random error of MEMS gyroscope was effectively restrained.

Key words：MEMS gyroscope；time-sequence model；on-line modeling；Kalman filter

doi：EEACC：2575；7220；763010.3969/j.issn.1004-1699.2016.01.014

收稿日期：2015-07-23修改日期：2015-09-20

中图分类号：TP39；TP183；TP212

文献标识码：A

文章编号：1004-1699（2016）01-0069-06

项目来源：国家自然科学基金项目（51274118，70971059）；辽宁省科技攻关项目（2011229011）；辽宁省教育厅基金项目（L2012119）