立足三个方面，培养小学生几何直观能力

江苏连云港市青口中心小学（222100）乔玲玲



立足三个方面，培养小学生几何直观能力

江苏连云港市青口中心小学（222100）乔玲玲

［摘要］几何直观贯穿数学教学的始终，它凭借图形的直观性特点，使复杂的问题简单化，能够有效帮助学生深入数学本质，发展数学思维。在小学数学教学中，教师要立足画图策略、空间几何、数形结合三个方面，培养学生的几何直观能力。

［关键词］几何直观小学数学教学策略

几何直观，是指借助直观图形进行思维感知的一种数学能力。在小学数学教学中，几何直观贯穿教学始终，是发展学生智力的核心内容。教学中，如何才能在课堂中发挥几何直观的作用，建构小学生几何直观能力？

一、立足画图策略，运用数学表征

在小学数学学习中，大多数学生头脑中难以形成直观的几何模型，导致解题思路混乱。究其原因，与学生缺乏画图策略分不开。基于此，教师要培养学生看图、读图、作图的能力，帮助学生建构画图策略，使其学会运用数学表征分析和解决问题，逐步提高几何直观能力。

例如，“分数应用题”的一道习题：将一根绳子剪去20%后又接上了5米，比原来短了3米，这根绳子原来长多少米？因为这道题中的数量关系比较复杂，学生初看题目感到毫无头绪。此时我引导学生采用画图的方法梳理数量关系，将已知和未知一一呈现出来：

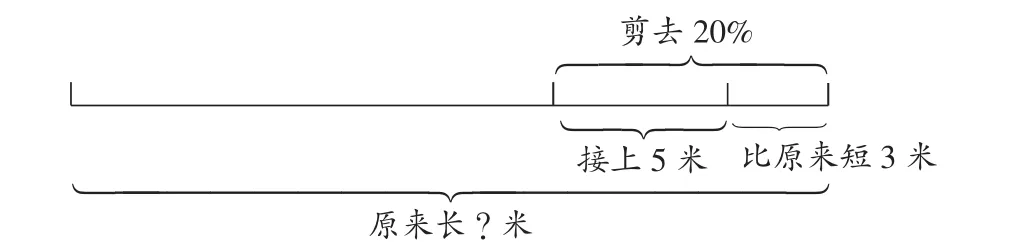
图1

在图中可以清楚看到，绳子原来的长度是未知的，已知条件是原来长度的20%被剪去后再加上5米比原来短3米。由此学生可根据线段图列出等量关系式，即“原来长度的80%”＋5等于“原来的长度－3”。设原来长度为x，则列出方程式“80%x＋5＝x－3”，得到结果为40米。我追问：“想一想，你从这道题中获得了什么启示？”学生认为，遇到这样复杂的应用题时，要先用线段图梳理数量关系，找出直观的数学表征，而后进行分析，从而找到完满的解决方案。

在以上教学环节中，教师立足画图策略，带领学生紧扣已知和未知进行数量关系的梳理，引导学生采用线段图进行分析，使学生很快找到问题的核心所在，实现几何直观能力的发展。

二、立足空间观念，培养想象能力

课程标准已将空间观念作为一个主要目标。何谓空间观念？在小学阶段，具体包含以下几个方面：其一，根据物体特征抽象出几何图形；其二，根据几何图形想象出所描述的实际物体；其三，能够想象出物体的方位和相互之间的位置关系；其四，能够描述图形的运动和变化。在教学中，教师可借助几何直观，发展学生的空间观念，培养学生的数学想象能力。

例如，教学“长方体和正方体的体积和表面积”时，我设计了空间想象的教学活动：先在黑板画出长方体的六个面，然后擦去面，紧接着擦去几条棱，让学生根据剩下的三条棱确定长方体的形状。学生通过棱的信息，想象对应的面，从而确定长方体的形状（如图2）。

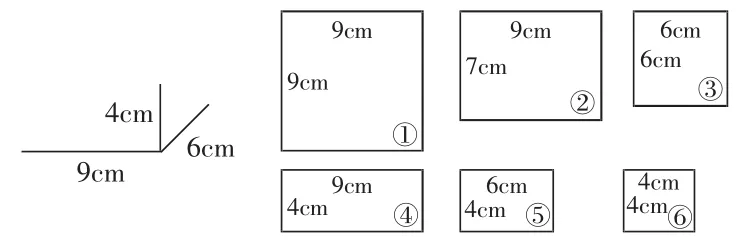
图2

教师通过擦去面和棱，帮助学生建立面的特征，并由线到面再到体，从一维到二维再到三维，使学生通过提取和分析表象，对长方体有了深刻认知。学生不但在想象中逐步建构了空间观念，还大大提升了空间想象能力。

三、立足数形结合，促进直观感知

数形结合不但在数学中应用广泛，在日常生活中也有很大的作用。在教学中，教师不但要借助图形，将抽象的数学概念变得直观简单，还要将图形问题转化为代数问题，使问题表达更加精确。“数”和“形”的相互渗透，不仅使解题简洁明了，还利于学生几何直观能力的形成。

例如，“乘法口诀”的习题：如图3所示，一个小三角形表示数字5，那么这个大三角形表示数字几？请列式计算。

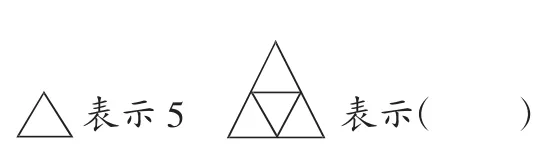
图3

学生一开始完全摸不着头脑，不知道该如何解决。此时我围绕数与形展开引导，让学生观察大三角形里有几个小三角形。学生很快得出共有4个小三角形。我问：“4个小三角形能用什么数字表示？为什么？”学生根据乘法的意义，认为这是表示4个5相加，可以通过乘法计算，列出算式“4×5＝20”。

通过这样的教学设计，学生领悟到数中有形、形中有数，有效突破了数与形的界限，促进了学生对数和形的直观感知。

总之，学生几何直观能力的培养并非一朝一夕就能完成的，教师要使抽象的问题直观化、隐蔽的问题明朗化，才能够有效帮助学生深入数学本质，使学生的几何直观能力得到长足的发展。

（责编金铃）

［中图分类号］G623.5

［文献标识码］A

［文章编号］1007-9068（2016）01-081