心有灵犀怎点通

江苏南京市长江路小学（210018）丁爱平



心有灵犀怎点通

江苏南京市长江路小学（210018）丁爱平

［摘要］理解学生是“为促进学习而教”的基础。剖析现状，重点从实践层面提出“绝对信任——‘理解学生’的情感动力，智慧倾听——‘理解学生’的客观前提，巧妙替换——‘理解学生’的智能秘钥”等操作策略。

［关键词］数学教学心有灵犀理解学生

理解学生是“为促进学习而教”的基础。如果教师缺乏对学生的理解，那么他的教学将是一厢情愿、一身疲惫与一声叹息。面对精灵一般的学生，我们反反复复地追问着：他们到底在想什么？师生之间如何才能心有灵犀、息息相通？

一、其实你不懂我的心：教师思维与学生思维的尴尬误解

1．现象之一：教师思维强势，禁锢学生思维

【案例1】不就和我的一样嘛！

三年级下册的笔算“25×30”。学生独立尝试，教师给出如右解答：

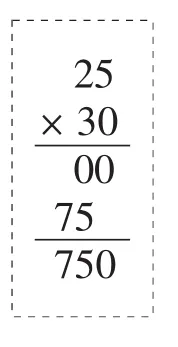
师：看到这个计算方法，你有什么想说的？

生1：0乘25没有任何意义——

师（立刻打断）：啊？0乘25没有意义吗？

生（肯定地）：嗯。

师：我们做过0乘几的算式题吗？（生都说做过）

师：0乘任何数都等于0啊！是有意义的。再仔细看看，这个竖式有什么问题？

生2：第一步的两个0太麻烦了，可以直接算25×3，再加一个0。

师（微笑）：请你到黑板上写出来！生1（嘀咕）：不就和我的一样嘛！

我曾经多次在这个班上过课。生1思维活跃、自由大胆。听课时，当我听到生1“0×25没有任何意义”这句话时，直觉告诉我，他想说的是“0×25反正等于0，没有必要先乘一遍”。而执教的教师抓住“0乘25没有意义”的字面含义来做文章，用“是否做过0乘几的算式题”来反驳学生，教师思维是很清晰的：如果算式没有意义，则算式不存在。问题是，学生的思维与教师的思维并不同步。在此，学生的思维呈现两种不同的层面：其一，0×25等于0，没有必要计算这一步，学生口中所说的“没有意义”即“没有必要”；其二，0乘25等于0，“等于0”就是表示没有意义。第二层面的学生思维仅仅是本节课的一个非核心目标的小知识点，教师应积极回应第一层面的学生思维，挖掘出它的价值，然后再厘清“0×25＝0”的意义。因此生1对教师存在极大的不满，就在于教师过于强势，缺乏对学生思维的理解。

2．现象之二：标准答案横行，打压学生思维

【案例2】哪里有5啊？

“用乘法口诀求商”的例题：10个小朋友打乒乓球，2人一组，一共可以分成几组？

生1：二五一十。

师：题目里哪里有5啊？（生1悻悻坐下）

生2：10除以5等于2。

师：哪里有5啊？嗯，再想想怎么列式呢？

生3：10除以2等于5。（师满意地笑了）

教师心中高高悬挂着标准答案，对于学生的想法如同检测产品，不完全相同的一概果断扔掉。学生是怎样考虑问题的？生1想的是“求几个2是10？”这难道没有合理性吗？生2在听到教师“枪毙”乘法的声音后，立马换成了除法。生3想：前两个都不对，就剩下10除以2等于5了。教师对答案的苛求貌似严谨，实则严重打压了学生思维的灵性。

二、心有灵犀一点通：教师“理解学生”的方法寻绎

1．绝对信任——“理解学生”的情感动力

人与人之间需要平等和民主与理解和信任。印度诗人泰戈尔说过：“爱和信任是理解的别名。”在数学课上，教师不要总是紧紧地攥着“对不对”“严密不严密”来苛求学生，要充分地信任学生，当学生的言说不够准确、不够全面时，不要用怀疑的语调、手势或立刻换人补充纠正，而是要大胆地相信他！舍得花时间，让他把心里的想法说出来、说下去。上述案例1中，如果教师一开始不是武断地打断生1的发言，而是让他把话说完，教学的境界就大不同了。

2．智慧倾听——“理解学生”的客观前提

当下，“能讲”的数学教师在某种意义上比不上“会听”的教师。周星驰在一部电影中有一句经典台词：“你不说，我怎么知道？”放在教学中，教师要理解学生的思维，一定要认真倾听学生的所思所想。课堂上，学生能说的，教师“闭嘴”；学生说错的，教师不轻易“插嘴”；学生实在说不出，教师才“动嘴”。

【案例3】真的是180°吗？

教学“三角形的内角和”时，我问：“三角形的内角和真的是180°吗？”学生马上说“是”。我请学生大声读这句话，读着读着，学生陷入了沉思……

生1：大家看我这个三角板，90°＋45°＋45°＝180°。真的是180°！

生3：你这样还是三角形吗？

生2：我是反着想的，如果内角和不是180°，它就不是三角形。（生恍然大悟）

生4：我画一个长方形，分成两个一样的三角形，用360°÷2＝180°。（生鼓掌）

生5：我把平行四边形分成两个一样的三角形，可是怎么得出“125°＋30°＋30°＝185°”？

生6：我直接画了一个三角形，测量后发现内角和真的是180°。

生7：不如全班每个人都画不同的三角形，再量量看是不是180°？

生8：画来画去总共就48个三角形，你怎么知道世界上所有的三角形都是这样？

生9：量的方法不好，量角器多一点点少一点点，都会有误差。

生10：三角形内角和是180°。这句话是人为制造的，他们当时制造的时候也会有误差，那么用有误差的方法得到的观点还对吗？（师生都懵了）

生11：就算量的方法有误差，也是量角器和人有误差，不是三角形的内角和有误差！

（其他学生愣了一会儿后鼓起了掌）

学生不断地跳出他人的思路，质疑有力：用三角板来举例说明——从反面去思考——借助四边形的分割，发现测量法——48个例子的不完全归纳似乎水到渠成——被生10的“误差制造论”打破，师生都懵了——生11斩钉截铁的回应又缓解了氛围——认可从长方形里的分割——课后继续“破译”。高质量的质疑、分析、再质疑、再分析……教师几乎插不上嘴，也没有必要插嘴。教师这种看似无为的倾听其实是一种智慧，是在倾听中理解着学生的理解。

在大班化教学中，教师要在40分钟内无一遗漏地倾听每一个学生的表达根本不可能，因此可以让学生写，写出课堂上意犹未尽的思考，一张简单的小纸条、QQ留言、电子邮件，都可以跟教师互动交流。这样的方式满足了学生一吐为快的愿望，也让教师对学生的思维有了更深的理解。

3．巧妙替换——“理解学生”的智能秘钥

一边是学生的自由不羁和天真烂漫，一边是数学特有的理性精神。如果教师死死抱着成人思维的模式，缺失对学生思维的揣摩、假想、预演，那么他所教的数学必定是生涩而冷漠的，难以走进学生心灵的。教师要乐于做一个长大的学生，经常有滋有味地想：如果我是学生，会怎么想呢？在一次次思维乃至精神的替换中走近学生、理解学生。

【案例4】不是很容易吗？

教学“乘法分配律”后，我给出一道练习题“29×19＋29”，很多学生不会做。“奇怪，这不是很容易的吗？”但我没有急于询问学生的困惑所在，而是试着把自己当成学生，把课件再看一遍，课本上的以及这两天的补充练习再浏览一遍，发现所做的练习都是“提取一个非整十数，另外两个乘数一定能凑成整十数或整百数”。在“29×19＋29”中，29和19都有凑整的趋势，找不到鲜明的非整十数。原来，凑整的条件反射已经形成，算式本身的意义、结构却被忽略掉了。我把自己的想法讲述给学生听，他们在惊讶中更多了一份亲昵。

当天家庭作业中有一题“99×37＋99＝□×（□＋□）”，又有学生写为“37×（99＋1）”。“奇怪了，刚刚上过凑整的当，怎么一转身就忘了呢？”我努力让自己跳脱批改作业的情境，回到师生分享“29×19＋29”的画面……“19个29加上1个29等于20个29，如果当成19×30，计算虽然很简便，但是意思是错的”。原来学生认为，无论算式的意义、结构如何，运用乘法分配律一定是为了计算简便。简便，始终占据上风。再看这道题，如果写成99×（37＋1），99×38一点都不简便啊，那肯定是用错运算律了。我又回到学生中间，询问他们的想法，果然与我不谋而合。

在教学中，很多教师站在“教”的高岗上，把数学“投递”给下面的学生，俯瞰着学生的学习表现，面对学生的错误，他们很焦虑，该讲的都讲了，该练的也都练了，学生是怎么回事啊？其实，只要教师能够站在“学”的层面上，试着用学生的思维思考问题，就能循着学生的思维轨迹，找到问题的所在，获得对学生的宽容与理解。

总之，学生是一个跳跃着的精灵，他们无时无刻不在获得新的生长。因此，理解学生，也许是一个永远也无法穷尽答案的命题，但我们将付出全部的爱与智慧，和学生相知相和、心有灵犀，共同徜徉在美好的教学之境。

（责编金铃）

［中图分类号］G623.5

［文献标识码］A

［文章编号］1007-9068（2016）01-017