挖隐含 构函数 巧证数字型不等式
2016-03-18 05:54甘肃魏正清
教学考试(高考数学) 2016年3期
甘肃 魏正清
挖隐含 构函数 巧证数字型不等式
甘肃 魏正清
近几年高考压轴题中的有些数字型不等式,若从正面去直接证明,往往感到非常棘手,但若能深入研究不等式本身的结构特征,挖掘潜在信息,从题目已知的函数入手,恰当的取特值,巧妙的构造函数模型,构造恒成立不等式,常常会出其不意,攻其不备,巧妙破解一类高考压轴题.本文例述证明这类数字型不等式的模式化策略.
【例1】(2011·全国Ⅱ理)(1)设函数f(x)=ln(1+x)-,证明:当x>0时,f(x)>0;
(2)从编号1到100的100张卡片中每次随机抽取一张,然后放回,用这种方式连续抽取20次,设抽得的20个号码互不相同的概率为p.
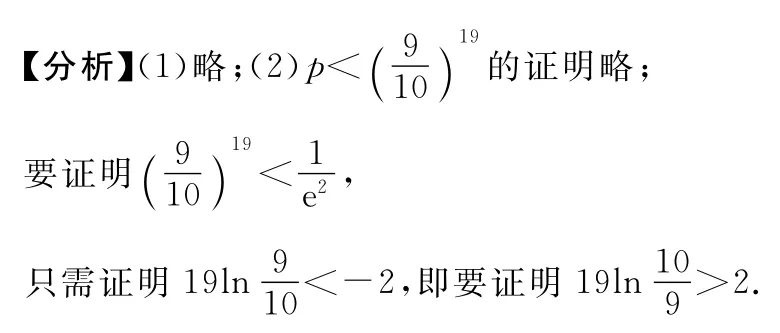
潜在信息 只需证明对数小于或大于某个常数,也就是需要构造对数不等式.
隐含条件 由(1)知当x>0时,f(x)>0恒成立.

【例2】(2014·新课标Ⅱ理)已知函数f(x)=exe-x-2x.
(1)讨论f(x)的单调性;
(2)设g(x)=f2(x)-4bf(x),当x>0时,g(x)>0,求b的最大值;

潜在信息1 只需寻求对数不等式.
隐含条件1 由(2)知当b≤2时,g(x)>0恒成立.

(1)求常数b的值;
(2)当0≤x≤1时,关于x的不等式f(x)≥0恒成立,求实数a的取值范围;

于是当x∈(0,1)时,g(x)<0,得f′(x)<0,故f(x)在(0,1)上单调递减.
从而f(x)<0,x∈(0,1)恒成立.
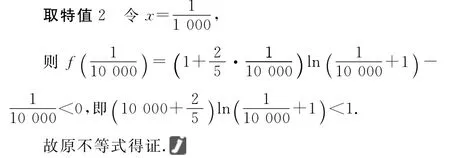
(作者单位:甘肃省临泽一中)
猜你喜欢
中学生数理化(高中版.高二数学)(2022年6期)2022-06-30
中学生数理化(高中版.高二数学)(2022年6期)2022-06-30
数学物理学报(2022年2期)2022-04-26
新世纪智能(数学备考)(2021年9期)2021-11-24
中学生数理化(高中版.高二数学)(2021年4期)2021-07-20
数学年刊A辑(中文版)(2021年1期)2021-06-09
新世纪智能(数学备考)(2020年9期)2021-01-04
中学数学杂志(初中版)(2019年4期)2019-09-18
中学生数理化·高一版(2018年10期)2018-11-08
山西大同大学学报(自然科学版)(2016年4期)2016-11-27

