基本不等式解题“五先五后”策略
2016-03-18 05:54陕西特级教师
教学考试(高考数学) 2016年3期
陕西 李 歆(特级教师)
基本不等式解题“五先五后”策略
陕西 李 歆(特级教师)
基本不等式是高中数学的重要内容,是求解函数最值和证明不等式的重要工具,也是高考中常考的重要知识点.但同学们在解题时,因对基本不等式的“内涵”理解肤浅,对数学问题的“题情”识别不清,导致二者之间的“嫁接”链条缺失,造成解题的出错率往往较高,有鉴于此,本文介绍基本不等式解题的“五先五后”策略,供同学们复习时参考.
一、先变形,后拆项

二、先判断,后添项

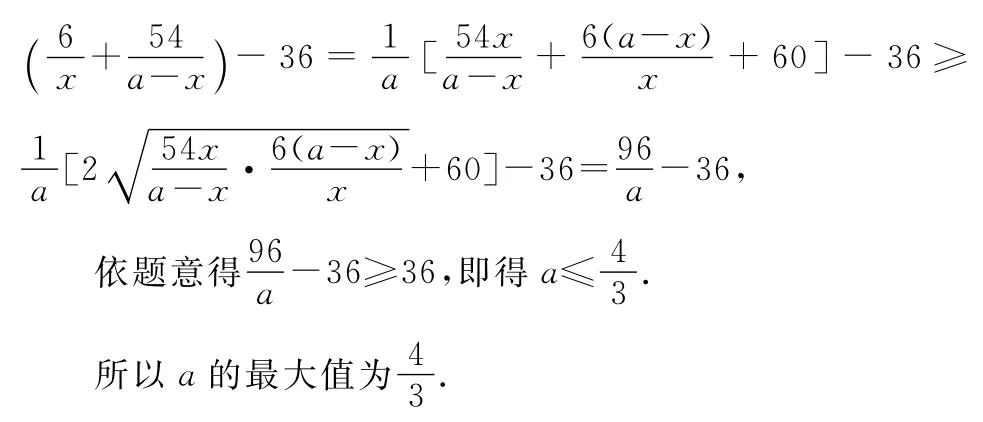
【点拨】(1)“1”的代换法是数学中最常用的一种解题方法,此解正是通过的巧妙实施,才使解题顺利通畅,达到了“山重水复疑无路,柳岸花明又一村”的效果.

三、先放缩,后叠乘

【分析】这是一个数列不等式,通常用数学归纳法证明,但从k到k+1难度较大,注意到不等式左边每一项中的分数分母依次相差2,可考虑依次先将前面分数的分子变为后面分数的分母,然后利用基本不等式放缩后再用叠乘的方法解决.

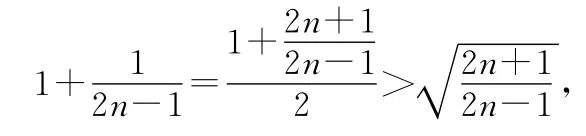
以上各式两边分别相乘,得

【点拨】数列不等式的证明,是高考考查的热点和重点.解这类问题,要从不等式内在的结构特点入手,寻找突破口.此解通过把不等式左边乘积中的各项,分别转化为两个数的平均数的形式,从而为应用基本不等式搭起了一个平台,使问题解决精彩绝妙.
四、先分离,后消元
【例4】已知x,y∈R+,且x-y=xy,x-4y-a=0,求实数a的取值范围.
【分析】实数a在条件等式x-4y-a=0中,可知a=x-4y,但此式含有两个未知数x和y,可由另一个条件等式x-y=xy中把x或y分离出来,然后代入求解.

【点拨】此题也可以利用“1”的变形技巧求解:由x-y= xy,得,则,以下略.
五、先引参,后代入

(作者单位:陕西省武功县教育局教研室)
猜你喜欢
中学生数理化·七年级数学人教版(2021年11期)2021-12-06
中学生天地(C版)(2021年4期)2021-04-22
中学生天地(C版)(2021年2期)2021-03-01
中学生数理化·七年级数学人教版(2020年11期)2020-12-14
数学小灵通(1-2年级)(2020年9期)2020-10-27
福建基础教育研究(2019年1期)2019-09-10
中学生数理化·七年级数学人教版(2019年11期)2019-09-10
福建基础教育研究(2019年1期)2019-05-28
新高考·高一数学(2018年5期)2018-11-22
读写算(中)(2015年11期)2015-11-07

