一类含有等式的向量题的解题方法
浙江 李承法
一类含有等式的向量题的解题方法
浙江 李承法
向量题目常有等式c=λa+μb(λ,μ∈R)出现,对于这类等式相关问题处理得当,可有效提高解题效率.笔者就此类问题常用的解题方法作了整理,以飨读者.
一、两边平方法

【评注】将等式化为c=λa+μb(λ,μ∈R)形式后,若已知其中的向量模或夹角的,可采用两边平方法求得问题的解.
【变式练习】在平面上给定边长为1的正三角形OAB,动点C满足,则点C的轨迹为( )
A.线段 B.圆 C.椭圆 D.双曲线

二、两边数量积法

A.30° B.45°
C.60° D.90°

【评注】已知向量等式中有关向量的模或夹角的,可以在等式两边同时乘上适当的向量,得到方程或方程组,从而求得问题的解.

A.外心B.内心
C.重心D.垂心


三、几何法
【例4】O是平面上一定点,A,B,C是平面上不共线的三点,动点P满足则动点P的轨迹一定通过△ABC的( )
A.外心 B.内心
C.重心 D.垂心




【评注】利用向量加法的平行四边形法则或者平面向量基本定理,图形的几何性质(本例运用解直角三角形)数形结合来处理,直观易解.



四、坐标法
【例6】(2013·温州一模)已知平面向量a,b,e,满足|e|=1,a·e=1,b·e=2,|a-b|=2,则a·b的最小值是________.
【解析】设e=(1,0),a=(x,y),b=(m,n),则可得x=1,m=2,∴a=(1,y),b=(2,n),由|a-b|=2得|(-1,yn)|=2,∴1+(y-n)2=4,(y-n)2=3,即y2+n2=2yn+3,又y2+n2≥-2yn,∴y2+n2=2yn+3≥-2yn,∴yn≥
【评注】在题设条件中有多个向量等式时,用向量的坐标来转化方程(组)或者不等式组来求解.
【变式练习】(2015·浙江模拟)已知向量a⊥b,|a-b|=2,定义:cλ=λa+(1-λ)b,其中0≤λ≤1,若,则|cλ|的最大值为( )


五、投影定义法
【例7】如图4,O为△ABC的外心,AB=4,AC=2,∠BAC为钝角,M是边BC的中点,则的值为( )
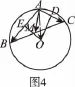
A.4B.5C.7D.9

【变式练习】(2013·温州一模)已知平面向量a,b,e,满足|e|=1,a·e=1,b·e=2,|a-b|=2,则a·b的最小值为____________.
【简解】如图5,设e,a,b都以O为起点,终点分别为E,A,B,由向量数量积的几何意义知,点A在垂直于e的直线l1上,且O到直线l1的距离为1,点B在垂直于e的直线l2上,且O到直线l2的距离为2,由|a-b|=2知,|AB|=2,设M为线段AB的中点,由向量积化恒等式得a·b=,因此求a·b的最小值就转化为求|OM|的最小值.显然点M的轨迹为垂直于e的一条直线l3,而O到直线l3的距离为

在各地模拟题和高考题中,含有c=λa+μb(λ,μ∈R)的向量题屡屡出现,常考常新,对这样的向量试题不应该惧怕,综上可知用向量的“数”和“形”两个属性,运用两边平方,两边数量积,坐标法或几何法,涉及平面向量数量积的问题还可以用投影—数量积几何意义或者向量积化恒等式来求解,可以有效解决问题.
(作者单位:浙江省开化中学)

