含参导数问题的五种求解策略
甘肃 张建虎
含参导数问题的五种求解策略
甘肃 张建虎
以函数为载体,以导数为工具,考查函数性质及导数应用为目标,是最近几年函数与导数交汇试题的显著特点和命题趋向.运用导数确定含参数函数的参数取值范围是一类常见的探索性问题,主要是求存在性问题或恒成立问题中的参数的范围.解决这类问题,主要是运用等价转化的数学思想,通过分离参数、数形结合、分类讨论等思维方法进行求解.而求解策略的恰当选择,取决于求解策略是否准确,本文就此类含参数的导数问题做如下阐述.
1.分离参数,化为最值问题
(1)当a=1时,求函数f(x)的单调区间和极值;
(2)当x∈[1,2]时,不等式f(x)>2恒成立,求a的取值范围.

【评注】本题中,参数a可以用含x的函数来表示,因此想到分离参数,进而转化为最值问题.上述解法可以实施的前提是变量a可以比较方便地“分离”出来,用含x的函数来表示,且可以确定新函数g(x)=f′(x)在区间(-1,1)是单调递增的.若变量a无法分离,或新函数h(x)的单调性无法确定(h(x)存在极值点,但又无法求出此极值点),那“分离参数”这个方法在此就不合适了.为此,本题还提供一种对此类问题的一般性解法.
【变式练习】设函数f(x)=kx3-3x+1,x∈R,若对于任意x∈[-1,1]都有f(x)≥0成立,求k的取值范围.
【提示】分x>0,x=0,x<0依次讨论并对k的取值范围求交集,即得k=4.
2.分类讨论,逐一分析
题目见【例1】

【评注】虽然解法一可以避免分类讨论,简洁程度明显优于解法二.但解法二给出了求函数最值的基本方法,适用范围较广,也要引起足够的重视.
【变式练习】函数f(x)的导数f′(x)=a(x+1)(x-a),若f(x)在x=a处取得极大值,求实数a的取值范围.
【提示】对a进行逐一分类讨论.答案是a∈(-1,0).
3.化为以参数为新变元的问题
【例2】 已知函数f(x)=x2+alnx-2,若f(x)+1≥0恒成立,求实数a的取值范围.
【分析】本题虽然可以分离参数,但需对lnx是否大于0讨论,这样一个问题变成了两个问题,比较浪费时间.

∴a=-2是φ(a)的极大值点,也是φ(a)的最大值点.
∴φ(a)≤φ(-2)=0,又φ(a)≥0,∴a=-2,即a∈{-2}.
【评注】“分离参数”的解法虽然比较简洁,但有一定的局限性.当分离参数的方法受阻时,只能转为直接求最值,同时,分离参数后,对新函数的导函数讨论会陷入既无法定号、又无法求出极值点的尴尬境地,因此不适合用分离参数解决.只能直接对f(x)求导,讨论其单调性,求出f(x)最小值(是一个关于a的函数),进而转化为对关于参数a的函数的分析.

4.逆推求函数最值,进而得出参数范围
【例3】(2012·新课标卷)设函数f(x)=ex-ax-2.
(1)求f(x)的单调区间;
(2)若a=1,k为整数,且当x>0时,(x-k)f′(x)+x+1>0,求k的最大值.
【解析】(1)f(x)的定义域为(-∞,+∞),f′(x)=ex-a.
若a≤0,则f′(x)>0,f(x)在(-∞,+∞)单调递增.
若a>0,则当x∈(-∞,lna)时,f′(x)<0;当x∈(lna,+∞)时,f′(x)>0,所以f(x)在(-∞,lna)上单调递减,在(lna,+∞)上单调递增.
(2)由于a=1,所以(x-k)f′(x)+x+1=(x-k)(ex-1)+x+1.

由(1)知,函数h(x)=ex-x-2在(0,+∞)单调递增.而h(1)<0,h(2)>0,所以h(x)在(0,+∞)存在唯一的零点.故g′(x)在(0,+∞)存在唯一的零点.设此零点为α,则α∈(1,2).
当x∈(0,α)时,g′(x)<0;当x∈(α,+∞)时,g′(x)>0.所以g(x)在(0,+∞)的最小值为g(α).又由g′(α)=0,可得eα=α+2,所以g(α)=α+1∈(2,3).
由于①式等价于k<g(α),故整数k的最大值为2.
【评注】本题中,由于g′(x)不能直接定号,因此采取以g′(x)为新的起点,令h(x)=ex-ax-2,进而对h(x)进行求导分析.由对h′(x)的符号讨论得出h(x)的单调性,进而得出h(x)的最值;再由h(x)的符号,得出g(x)的单调性,进而得出g(x)的最值.可谓步步逆推,思维缜密.

5.数形结合解含参数的导数题
(解法1)代数逻辑逐一推理求解
直线l:y=kx-1与曲线y=f(x)没有公共点,等价于关于x的方程在R上没有实数解,即关于x的方程:在R上没有实数解.
令g(x)=xex,则有g′(x)=(x+1)ex,
当x∈(-∞,-1)时,g′(x)<0.所以g(x)单调递减;当x∈(-1,+∞)时,g′(x)>0.所以g(x)单调递增.故当x=-1时,,同时当x趋于+∞时,g(x)趋于+∞,所以g(x)的取值范围为
综上①②,得k的最大值为1.
(解法2)以“形”助“数”,图形直观求解
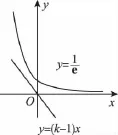
直线l:y=kx-1与曲线y=f(x)没有公共点,等价于关于x的方程在R上没有实数解,等价于函数的图象无交点.
【评注】画出与条件相对应的图形,实现“数”向“形”的转化,再根据“形”的特征及性质,建立符合条件的关系式,实现“形”向“数”的转化,这种“数”与“形”融为一体的解题方法,是解函数综合问题的重要方法.因此,巧妙运用“数形结合”思想解题,可以化抽象为具体,回避数的冗长与生涩难懂,效果事半功倍.
【变式练习】(2011·河南省联考)已知函数f(x)=x3+2x2-ax+1.若函数g(x)=f′(x)在区间(-1,1)上存在零点,求实数a的取值范围.
【提示】此题可以用分离参数转化为3x2+4x=a在区间(-1,1)上的有解问题,也可转化为直线y=a与曲线y=3x2+4x在(-1,1)上的交点问题,同时要数形结合.
(作者单位:甘肃省张掖市临泽一中)

