W=-ΔEp在弹簧问题中的应用题型剖析

郑行军

(福建省福鼎市第一中学,福建　福鼎　355200)



W=-ΔEp在弹簧问题中的应用题型剖析

郑行军

(福建省福鼎市第一中学,福建福鼎355200)

摘要：弹簧类问题多为综合性问题,弹簧在伸缩过程中涉及力、加速度、功和能等多个物理概念及其规律,此类问题具有很强的综合性,是高考的难点之一.利用模型化方法归纳出中学阶段出现的弹簧功能关系题型,使学生在分析此类问题时,能掌握有效的解题思路,可培养学生构建物理模型的思维能力和系统分析物理问题的能力.

关键词：弹簧;功能关系;形变量

1已知弹簧在某位置的弹性势能,利用W=-ΔEp直接求解

例1：如图1所示,轻质弹簧一端固定,另一端与质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h.圆环在C处获得一竖直向上的速度v,恰好能回到A，弹簧始终在弹性限度之内,重力加速度为g,则圆环().

图1

A． 在下滑过程中,加速度一直减小

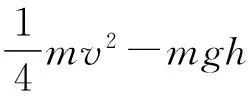
D． 上滑经过B的速度大于下滑经过B的速度

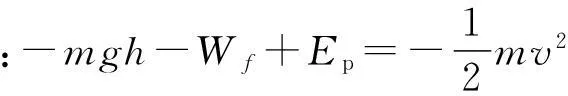
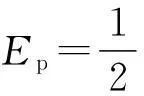
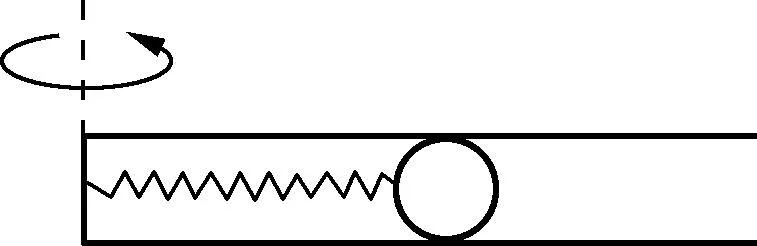
图2

A． 小球和弹簧组成的系统机械能守恒

3单物体连弹簧型

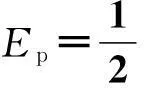
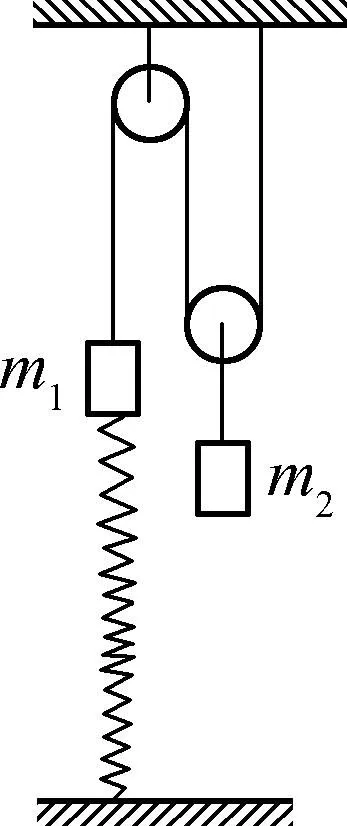
图3

例3：如图3是一组滑轮装置,绳子都处于竖直状态,不计绳子和滑轮质量及一切阻力,悬挂的两物体质量分别为m1=m,m2=4m,m1下端通过劲度系数为k的轻质弹簧与地面相连(重力加速度为g,轻质弹簧始终处于弹性限度之内)，求:

(1) 系统处于静止时弹簧的形变量;

(2) 用手托住m2且让m1静止在弹簧上,绳子绷直但无拉力,放手后两物体的运动发生在同一竖直平面内,求m2运动的最大速度．

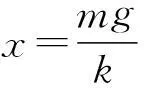
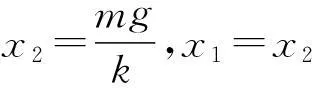
4多物体连弹簧型

该题型在设置题目条件时,应使前后两次弹簧的弹性势能增量绝对值相同,即|ΔEp1|=|ΔEp2|,分析题目时可先求出前后两次弹簧始末位置的形变量,得出|ΔEp1|=|ΔEp2|,进而得到|W1|=|W2|.利用形变量变化求出物体运动的位移,然后利用动能定理或能量守恒定律分别列出前后两次物体运动的方程求解.

图4

例4：如图4所示,用轻弹簧将质量均为m=1kg的物块A和B连接起来,将它们锁定在空中,弹簧处于原长状态,A距地面的高度h1=0.15m.同时释放两物块,设A与地面碰撞后速度立即变为零,由于B压缩弹簧后被反弹,使A刚好能离开地面(但不继续上升).已知弹簧的劲度系数k=100N/m,重力加速度g=10m/s2.

(1) 求物块A刚到达地面的速度;

(2) 求物块B反弹到最高点时弹簧的弹性势能;

(3) 若将B物块换为质量为2m的物块C(图中未画出),仍将它与A锁定在空中且弹簧处于原长,从A距地面的高度为h2处同时释放,C压缩弹簧被反弹后,A也刚好能离开地面,求此时h2的大小.

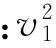
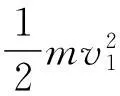
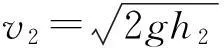
由以上例题分析可知,在解决弹簧功能关系问题时,如果能从模型入手,找出不同模型的特点及相应的解题方向,并以此为突破口分析物体的运动情况,运用物理规律进行解答,有关弹簧的功能问题都可以得到解决.

参考文献：

[1] 龚新志.弹簧类问题求解策略[J].物理教学探讨，2008，(3).

[2] 昊国法.功能关系在弹簧题型中之应用[J].理科考试研究，2014，(19).