电子-质子碰撞中的双强子关联现象
王宏民, 孙献静
(1. 装甲兵工程学院基础部, 北京 100072; 2. 中国科学院高能物理研究所, 北京 100049)
电子-质子碰撞中的双强子关联现象
王宏民1, 孙献静2
(1. 装甲兵工程学院基础部, 北京 100072; 2. 中国科学院高能物理研究所, 北京 100049)
通过分析不同色偶极模型得到的未积分胶子分布函数的适用性,选取了适用于碰撞能量较低的电子离子对撞机电子-质子深度非弹性散射实验的理论模型,并设计出一种能够解决当胶子动量分数较大时未积分胶子分布问题的数值方法。在此基础上,基于胶子饱和理论,在领头阶近似下研究了电子离子对撞机能量下电子-质子深度非弹性散射过程中的双强子关联现象。计算结果表明:理论值与在不考虑Sudakov效应下PYTHIA程序模拟出的实验结果基本一致。相关理论预言有待于电子离子对撞机实验验证。
双强子关联;胶子饱和机制;深度非弹性散射
双强子关联现象是研究硬散射过程中胶子内在动力学机制直接有效的途径,因此研究这一课题具有十分重要的物理意义。目前,美国相对论重离子对撞机(Relativistic Heavy Ion Collider,RHIC)测得了质子-质子以及氘核-金核碰撞过程中双强子关联现象的实验数据[1],并且研究者在胶子饱和理论框架下很好地解释了相关实验现象[2]。由于即将运行的电子离子对撞机(Electron-Ion Collider,EIC)将进行电子-质子(electron-proton,e-p)及电子-原子核(electron-nucleus,e-A)深度非弹性散射过程中双强子关联的实验测量[3],因此迫切需要关于e-p(A)深度非弹性散射过程中双强子关联现象的理论研究。由于电子离子对撞机双强子关联实验的碰撞能量较小(10 GeV×100 GeV和20 GeV×100 GeV),需要涉及到当胶子动量分数较大时未积分胶子分布函数的计算,因此选取适当的计算未积分胶子分布函数的理论模型是本文的难点。计算未积分胶子分布函数的模型和方法很多,如:CGC(Color Glass Condensate)模型[4]、AdS/CFT (Anti-de Sitter-space/Conformal Field Theory) 模型[5]、MV(McLerran-Venugopalan)模型[6]、GBW(Golec-Biernat Wusthoff)模型[7]以及考虑次领头阶修正的SF(Sudakov Factor)方法[8]等。此外,未积分胶子分布函数还可以通过求解rcBK(running coupling Balitsky-Kovchegov)或BK(Balitsky-Kovchegov)演化方程得到[9]。在以上模型和方法中,AdS/CFT模型和rcBK(或BK)演化方程适用于较小胶子动量分数区域;MV模型、GBW模型和SF方法适用于较大胶子动量分数区域。笔者将从其中选取适当的模型研究e-p深度非弹性散射过程中的双强子关联现象。
1 双强子关联的计算方法
双强子关联概率的定义式可以写为
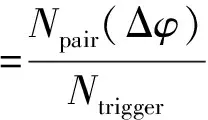
(1)
式中:Ntrigger为产生的触发强子数;Npair(Δφ)为产生的触发与伴生强子对,其中Δφ为触发和伴生强子之间的方位角。
在胶子饱和理论框架下,双强子关联函数可以表示为
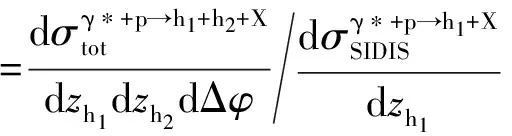
(2)

φ(xg,qT)Htot(zq,k1T,k2T)×
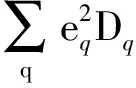
(3)
式中:C0为归一化因子;zq为夸克相对于入射虚光子的动量分数;zh1和zh2分别为触发强子和伴生强子相对于入射虚光子的动量分数;ph1T和ph2T分别为触发强子和伴生强子的横向动量;k1T和k2T分别为产生的夸克对中夸克和反夸克的横向动量,它们与ph1T和ph2T之间的关系可以表示为[11]
k1,2T=ph1,2T/(zh1,2/zq);
(4)
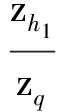
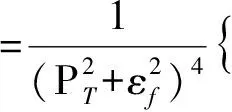
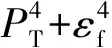
(5)

式(2)中分母为单举深度非弹性散射(Single-Inclusive Deep Inelastic Scattering, SIDIS)过程中强子产生截面,在领头阶近似下它可以表示为[11]
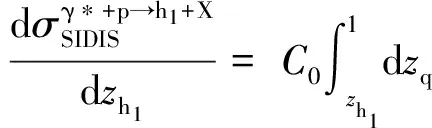
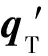
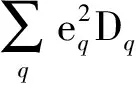
(6)
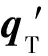
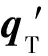
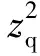
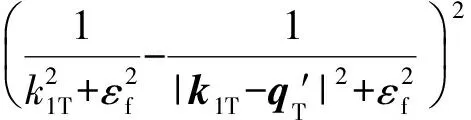
(7)
其中,y为虚光子与入射电子之间的能量分数。
2 适用于电子离子对撞机能量的色偶极模型
为了计算碰撞能量较小的电子离子对撞机e-p深度非弹性散射实验的碰撞截面,笔者选取了适用于求解胶子动量分数xg较大时未积分胶子分布函数的色偶极模型,即MV模型[6]、GBW模型[7]和SF模型[8]。3种模型的偶极散射振幅分别表示为
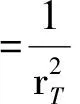
(8)
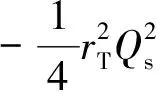
(9)
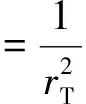
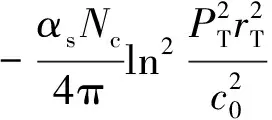
(10)
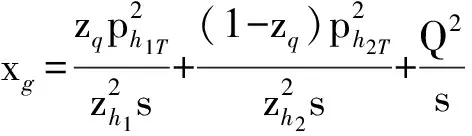
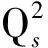
(11)
相对应的未积分胶子分布函数由偶极散射振幅通过傅里叶变换得到[14]:
φMV,GBW,SF(xg,qT) = ∫d2rTeiqT·rTNMV,GBW,SF(xg,rT) =
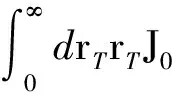
NMV,GBW,SF(xg,rT)。
(12)
式中:J0(rTqT)为第一类零阶贝塞尔函数[15]。
3 计算结果与讨论
3.1 不同模型的未积分胶子分布函数分布
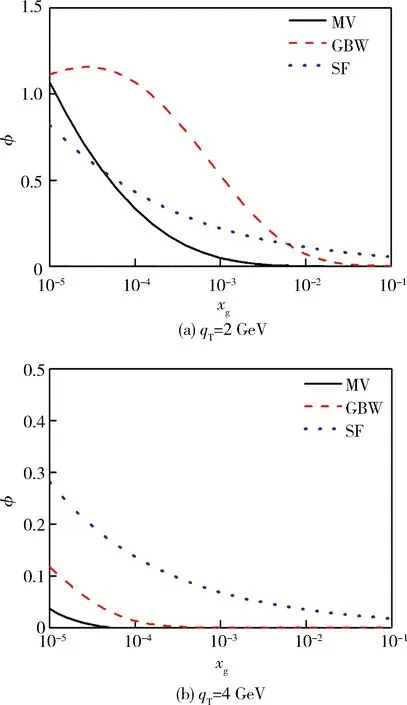
图1 不同模型的未积分胶子分布图
图1给出了qT=2、4 GeV时3种不同色偶极模型计算出的未积分胶子分布函数随胶子动量分数xg变化图。可以看出:1)当xg很大时,MV模型和GBW模型的数值趋于0, 说明当xg→0时这2个模型不适用;2)随着qT增大,3种模型的数值均急剧减小。
考虑图1的计算结果,同时注意到SF模型仅适用于考虑散射截面一阶修正情况,MV模型涉及对第一类零阶贝塞尔函数的高振荡积分[16],因此笔者采用GBW模型。GBW模型的优点在于可以由式(12)得到解析的未积分胶子分布函数:
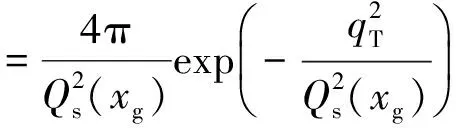
(13)
由于GBW模型在xg较大时不适用,因此当xg>0.01时笔者采用的未积分胶子分布函数为[11]
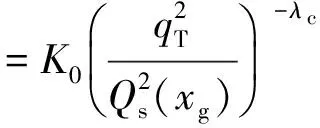
(14)
式中:K0为确保当xg=0.01时式(13)与式(14)相等而引入的常数;λc为异常维度。
3.2 e-p散射中π0介子双强子关联曲线
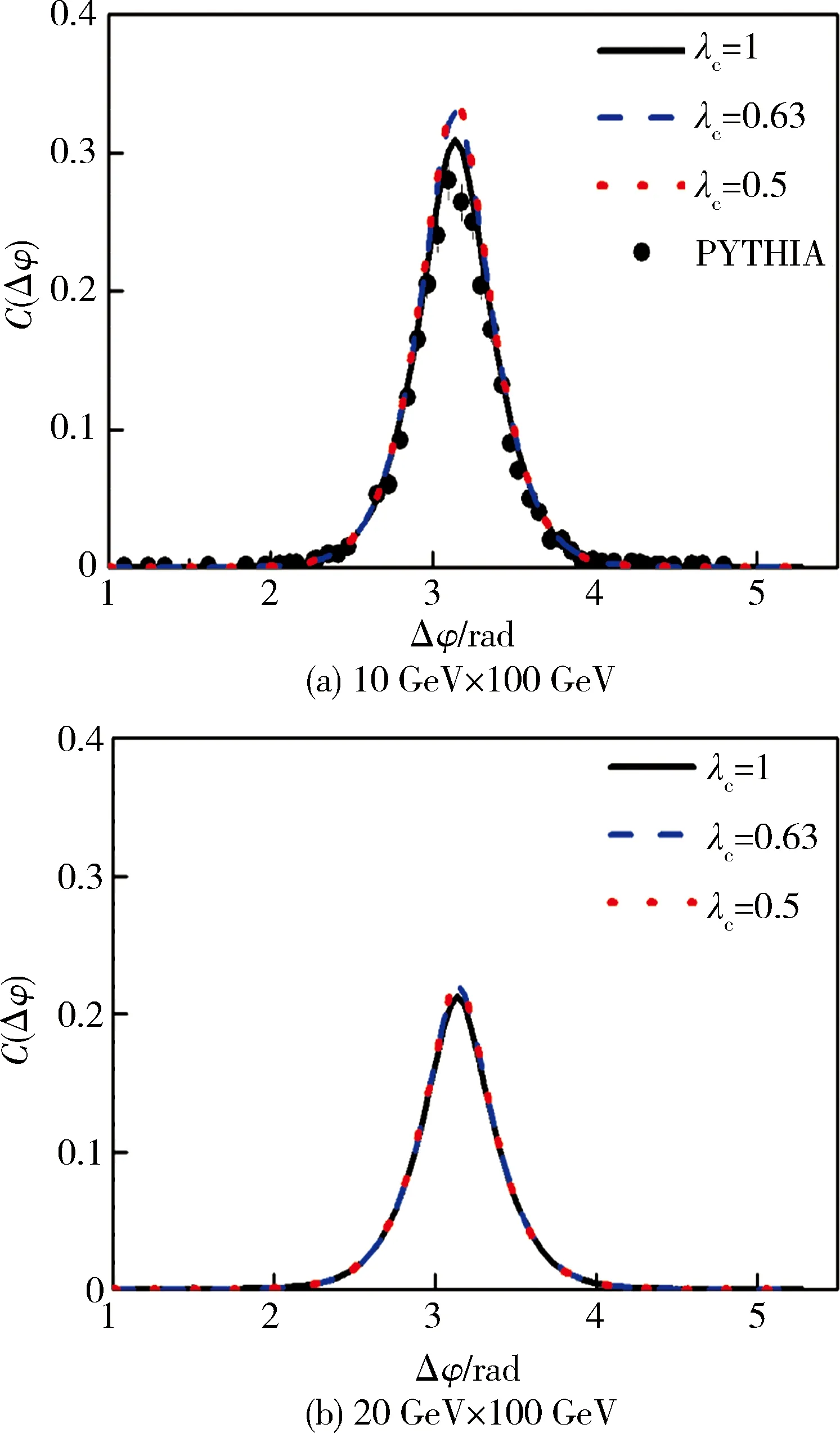
图2 e-p深度非强性散射过程中π0介子双强子关联曲线
图2给出了当碰撞能量分别为10 GeV×100 GeV和20 GeV×100 GeV时e-p深度非弹性散射过程中的π0介子产生的双强子关联曲线,各变量的取值区间分别为:1 GeV2 通过研究电子离子对撞机能量下的电子-质子深度非弹性散射过程中的双强子关联现象,可知胶子饱和理论是解决硬散射过程中双强子关联现象的有效方法。然而,本文没有考虑次领头阶修正的影响,这将是笔者下一步研究的重点。 [2] Stasto A, Xiao B W, Yuan F. Back-to-back Correlations of Di-hadrons in dAu Collisions at RHIC [J]. Phys Lett B, 2012, 716(3/4/5): 430-434. [3] Accardi A, Albacete J L, Anselmino M, et al. Electron Ion Collider: The Next QCD Frontier [EB/OL]. (2012-12-07)[2016-06-10]. http://arxiv.org/abs/1212.1701. [4] Watt G, Kowalski H. Impact Parameter Dependent Color Glass Condensate Dipole Model [J]. Phys Rev D, 2008, 78(1): 014016. [5] Kovchegov Y V, Lu Z, Rezaeian A H. Comparing AdS/CFT Calculations to HERA F2Data [J]. Phys Rev D, 2009, 80(7): 074023. [6] McLerran L, Venugopalan R. Computing Quark and Gluon Distribution Functions for Very Large Nuclei [J]. Phys Rev D, 1994, 49(5): 2233-2241. [7] Golec-Biernat K, Wusthoff M. Saturation Effects in Deep Inelastic Scattering at Low Q2and its Implications on Diffraction [J].Phys Rev D, 1999, 59(1): 014017. [8] Mueller A H, Xiao B W, Yuan F. Sudakov Double Logarithms Resummation in Hard Processes in the Small-x Saturation Formalism[J]. Phys Rev D, 2013, 88(11):114010. [9] Albacete J L, Armesto N, Milhano J G, et al. Nonlinear QCD Meets Data: A Global Analysis of Lepton-proton Scattering with Running Coupling Balitsky-Kovchegov Evolution [J]. Phys Rev D,2009,80(3):034031. [10] Dominguez F, Marquet C, Xiao B W, et al. Universality of Unintegrated Gluon Distributions at Small x [J]. Phys Rev D,2011,83(10):105005. [11] Marquet C, Xiao B W, Yuan F. Semi-inclusive Deep Inelastic Scattering at Small x [J]. Phys Lett B, 2009, 682(2):207-211. [12] Albino S, Kniehl B A, Kramer G. AKK Update: Improvements from New Theoretical Input and Experimental Data [J]. Nucl Phys B, 2008, 803(1/2):42-104. [13] Wang H M, Hou Z Y, Sun X J. Energy Dependent Growth of Nucleon and Inclusive Charged Hadron Distributions [J]. Chin Phys C, 2015, 39(11):114105. [14] Dumitru A, Hayashigaki A, Marian J J. The Color Glass Condensate and Hadron Production in the Forward Region [J]. Nucl Phys A, 2006, 765(3/4): 464-482. [15] 杨华军. 数学物理方法与计算机仿真[M]. 北京:电子工业出版社, 2006:373-375. [16] 王宏民, 任志明, 王洋,等. 重离子碰撞中的量子饱和机制 [J]. 装甲兵工程学院学报, 2010, 24(4): 85-87. [17] Altarelli G, Parisi G. Asymptotic Freedom in Parton Language [J]. Nucl Phys B, 1977, 126(2): 298-318. [18] Kovchegov Y V. Small-x F2Structure Function of a Nucleus Including Multiple Pomeron Exchanges [J]. Phys Rev D,1999,60(3): 034008. [19] Fadin V S, Lipatov L N. Next-to-leading Corrections to the BFKL Equation from Gluon and Quark Production [J]. Nucl Phys B, 1996, 477(3):767-805. [20] Zheng L, Aschenauer E C, Lee J H, et al. Probing Gluon Saturation through Dihadron Corrections at an Electron-Ion Collider [J]. Phys Rev D,2014,89(7):074037. (责任编辑:尚彩娟) Dihadron Correlations in Electron-proton Collisions WANG Hong-min1, SUN Xian-jing2 (1. Department of Fundamental Courses, Academy of Armored Force Engineering, Beijing 100072, China; 2. Institute of High Energy Physics, Chinese Academy of Science, Beijing 100049, China) By analyzing the applicability of the unintegrated gluon distribution functions obtained from different color dipole model, the model, which applies to the electron-proton deep inelastic scattering at electron ion collider with lower collision energy, is chosen. The method to solve the problem of the unintegrated gluon distribution at large gluon momentum fraction is designed. Then, in the gluon saturation formalism, the dihadron correlations in deep inelastic scattering from electron-proton collisions at electron ion collider energies are studied at leading order. It is shown that the theoretical results are in good agreement with the data from the PYTHIA simulations without Sudakov factor. The predictive results will be verified by the future electron ion collider experiments. dihadron correlations; gluon saturation formalism; deep inelastic scattering 1672-1497(2016)05-0107-04 2016-08-10 国家自然科学基金资助项目(11305195/A050509) 王宏民(1975-),男,副教授,博士。 O572.24+3 A 10.3969/j.issn.1672-1497.2016.05.0224 结论