基于BWDSP100的高性能FFT实现

(中国电子科技集团公司第三十八研究所孔径阵列与空间探测安徽省重点实验室， 安徽合肥 230088)

0 引言

随着数字技术的发展，基于时频域二维处理的算法以其优越的性能逐渐成为信号处理算法的主流，时域-频域间的相互转换成为数字信号处理中重要的一环。自从20世纪60年代库利图基发展出快速傅里叶变换(FFT)以来，FFT一直是时频域转换的首要工具。正是基于对FFT运算在诸多领域中广泛应用的重视， Freescale, TI, ADI等国际主流DSP芯片厂家纷纷采用FFT运行时间作为表征芯片性能的重要参数。对于一款高性能DSP而言，如何实现高效FFT运算是芯片走向实用的重要一环[1-2]。

1 芯片介绍

BWDSP100芯片(即“魂芯一号”)是中国电子科技集团公司第三十八研究所自主研发的一款高性能、超标量浮点运算DSP芯片。该处理器融合了多种现代芯片设计理念并加以扩展，充分发挥并行处理的优势和特点，可以满足大数据量、实时性要求高的数字信号处理、数据处理等工程应用要求。基于该芯片的雷达信号处理机已经完成设计，并在雷达数字阵列的大规模数字波束形成(DBF)中得到应用[3-5]。

BWDSP100采用宏作为基本处理模块。其片内拥有4个处理宏(X/Y/Z/T)，每个宏拥有4个乘法累加器、8个ALU运算器、2个移位器、1个特定运算单元及64个32位寄存器，内嵌28 Mbit SRAM(24 Mbit数据空间，4 Mbit程序空间)，单宏单周期内能够完成8次浮点加减法及4次浮点乘法运算。同时它也支持32位和16位定点运算。考虑到取数效率，BWDSP100内部拥有3个结构相同、相互独立工作的地址发生器(U/V/W)，可以通过来自译码器的立即数或者来自通用寄存器组的数据，对地址发生器的内部寄存器进行初始化。地址发生器利用这些初始化信息作为地址计算所需的基地址和偏移量。整个芯片内部架构如图1所示。

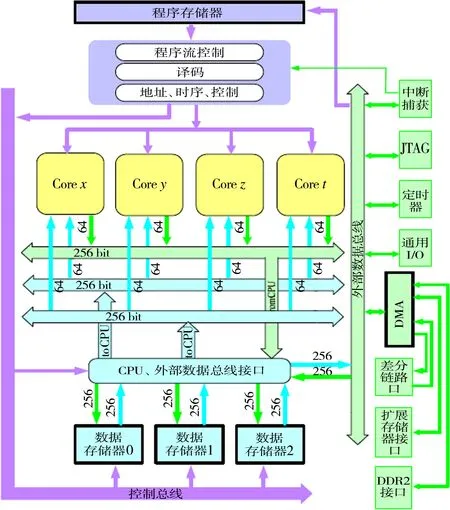
图1 BWDSP100内部架构

BWDSP100内部24 Mbit数据空间采用SRAM搭建而成，不存在Cache命中问题。整个存储部件分为3组(memory block)，分别称为B0，B1，B2，每组又由8个独立存储器组成，每个存储器的存储容量为32 K×32 bit。因而器件内部数据存储器总数为3×8=24个。这样的配置可以保证存储单元在数据传输高峰情况下能够同时提供两组256 bit的数据给执行核，与此同时接收一组从执行内核送过来的256 bit的数据。BWDSP100与ADI公司TS201设计性能比较如表1所示。不考虑读写带宽的前提下，BWDSP100的性能是TS201的8倍。

表1 BWDSP100与TS201的性能比较

2 算法选择

对于FFT算法来说，其数学表达虽然一致，但具体实现架构却千差万别。针对硬件特点选择合适的处理算法会让实际程序在处理性能、实用性等方面得到较大的提升。以ADI公司的TigerSHARC系列芯片为例，虽然TS201与TS101保持了指令向下兼容，但是同样的1 024点FFT，TS101的运行周期数为9 872，TS201的运行周期数却为12 170。在针对TS201的内部DRAM存储新特性改用SingLeton算法优化后，ADI提供的新程序1 024点FFT运行周期数为9 419，运算性能得到了明显提升。

因此，为了满足设计指标，必须针对BWDSP100结构特点对FFT算法架构进行选择，这样才可能贴近工程实际需要，充分发挥芯片特点，给出真正反映芯片性能的测试结果。

2.1 频域分解与时域分解

FFT算法可以分为频域分解(DIF)与时域分解(DIT)两种结构形式。两种结构的区别在于：频域分解是在两点DFT之后有旋转因子，时域分解是在两点DFT的节点之前有旋转因子。很显然，如果在第一级蝶形运算中加入适当的旋转因子，时域分解法的乘法系数可以完成对输入数据实部虚部的不等加权；如果在最后一级蝶形运算中加入适当的旋转因子，频域分解法的乘法系数可以实现对输出数据实部虚部的不等加权。从工程上看，时域分解法的不等加权既可以实现对前方数字化通道不一致的补偿，也可以实现对输入数据取共轭从而方便复用FFT程序得到IFFT的共轭结果。此时只要对输出结果取共轭就可以得到正常IFFT结果。相较于另外编写一套IFFT函数，复用FFT程序可以进一步减小程序体积，因此，基于BWDSP100的FFT标准函数采用时域分解FFT算法实现。

2.2 原位算法与非原位算法

原位(in-place)FFT运算是指在不附加缓冲的情况下，FFT的输入及输出结果可以在同一地址空间。非原位(not-in-place)FFT运算则指在不附加缓冲的情况下，输入及输出结果必须在不同地址空间。很明显，相较于非原位FFT运算，原位FFT占用的存储空间更少。

原位FFT必须通过位反序才能获得正确结果。2的n阶FFT需要进行n位的位反序。记某数s的二进制表现形式为(Sn-1Sn-2…S0)，则其对应的逆序数S为(S0S1…Sn-1)。相应的s称为原序数。将按原序排列的某个矢量改为按逆序排列的过程称为位反序操作。显然，对于连续原序数系列来说，其对应的逆序数序列必定非连续。在原位FFT实现中，如果单独增加一级位反序处理必然会降低程序效率，最好的办法是将位反序操作与蝶形运算结合起来，在运算中完成位反序。非原位FFT可以通过调整运算架构避免位反序操作。这种调整的代价是要么输入地址的数据在运算中被改写，要么必须增加额外缓冲。

位反序对程序效率的影响在于两点：计算逆序数导致的计算延迟和逆序本身引发取数不连续所导致的读写速度下降。现代DSP(包括BWDSP100芯片)大都具有逆序取数功能，逆序数的计算延迟可忽略不计；逆序循环可以保证取数的局部连续性，改善逆序读写带宽。逆序循环的实质在于提取s的最低m个比特与最高m个比特单独进行逆序交换。由于最低m个比特的顺序标号具有连续性，表现在存储上即具有地址临近的特点，所以采用逆序循环算法后可以连续读写以充分利用芯片带宽。同时由于逆序数与原序数间互为逆序，因此这种部分逆序交换的结果必然具有封闭性(即循环性)[6-7]。如果处理芯片内部寄存器足够，可以对循环体涉及到的数据进行暂存和重组，从而实现原位FFT。实际编程中为提升效率而引入了多级合并，此时BWDSP100芯片内部寄存器数量不足以支持这种暂存和重组操作。基于效率优先的考虑，最终选择了基于逆序循环的带位反序操作的非原位算法。在不增加额外缓冲的前提下，输入地址的数据在运算后也可以保留下来。其算法架构如图2所示。

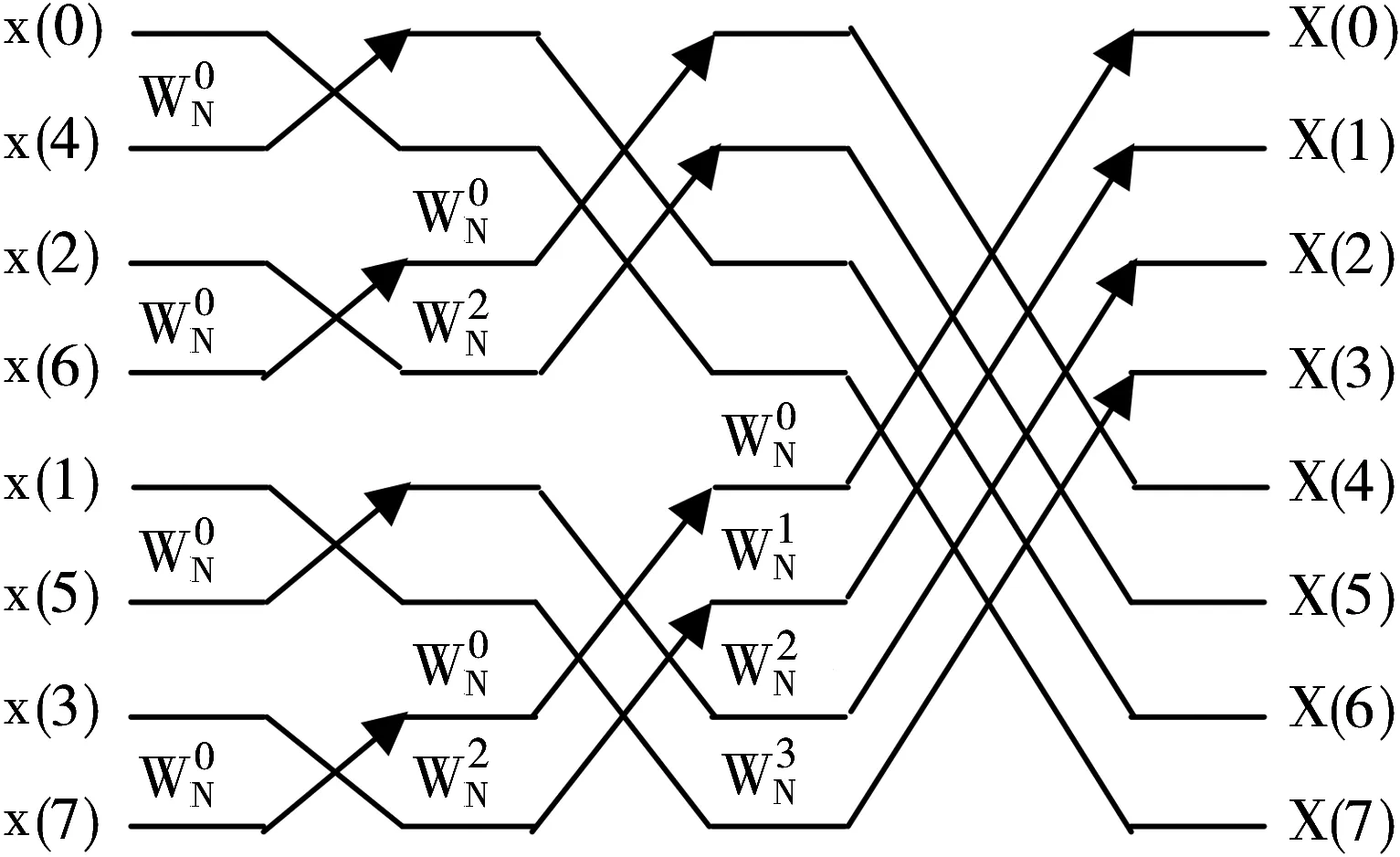
图2 8点时域分解原位FFT算法架构

3 算法实现

3.1 运算能力与IO能力的匹配

如前所述，BWDSP100芯片具有非常强大的浮点运算功能，其单核单周期内能够完成8次浮点加减法及4次浮点乘法运算。与之相比，BWDSP100芯片的数据吞吐能力略显不足，其单核单周期可以读取两个浮点复数(64 bit×2)，存储一个浮点复数(32 bit×1)。

FFT基本运算为形如(a+bj)±(c+dj)×(Wr+Wij)的蝶形运算。单个蝶形运算的运算量是4次浮点乘法和6次浮点加减法，对应芯片I/O能力的要求是读取3个浮点型复数(两个运算数、一个旋转因子)，存储两个浮点型复数(两个运算结果)。与BWDSP100芯片能力相比，BWDSP100可以在单周期内完成单个蝶形计算，但是无法在单周期内完成相应的IO操作。为了充分发挥芯片的运算性能，必须进行多阶合并。如果进行两阶合并的话，两个周期内要求芯片的I/O能力降低为：读取4个复数(两个运算数、两个旋转因子)，存储2个复数(两个运算结果)，BWDSP100芯片可以满足这一要求。由于此时乘法运算能力已经全部应用完毕，更多阶数的合并并不能带来更大的得益，反而造成程序复杂度增加。因此，两阶合并是比较合理的选择。

两阶合并带来的问题是FFT长度被强制要求为2的偶数次方，这在很多应用场合使用十分不便。观察图2可以发现，时域分解FFT算法的前两级均为特殊旋转因子(第一级为全1，第二级为1和-j)，这样单个蝶形运算只需要进行4次加减法。前后两级蝶形运算合并后共8次加减法，即使考虑到不等加权带来的4次乘法，两级运算一个周期即可完成。于是再次遇到了数据吞吐能力不足的问题。继续延用前面所提的多阶合并办法解决这个问题。多阶合并的最大限制由芯片运算核所拥有的内部存储器个数给出。由于BWDSP100芯片单核拥有64个内部存储器，合并阶数最高可以达到四阶。采用判断处理的办法。对于偶数阶，采用四阶合并；对于奇数阶，采用三阶合并。这样既解除了FFT长度必须为2的偶数次方限制，又提高了程序的运行效率。

3.2 充分发挥IO带宽

2.2节已经指出采用逆序循环可以充分发挥芯片的IO带宽。本节将对其具体实现作出说明。

在第1节已经指出，BWDSP100内部数据存储器分为3组，每组由8个32 bit独立存储器组成，合并为一组256 bit数据提供给4个执行核，每个核从中可以获得64 bit数据。8个32 bit独立存储器地址分布如图3所示。

图3 8个32 bit独立存储器地址分布图

如果拼成256 bit数据的几个地址落到了同一个存储器就会发生地址冲突。此时，程序流水会被打断，只有当冲突的数据按周期全部读写至各独立存储器的缓存后，程序才会继续执行。

流水打断会对读写带宽产生极大的影响，为了解决这个问题，在程序编制中应该尽量保证一组所取数据存放在不同存储器中。BWDSP100的位反序取数指令如下所示[6]：

{x,y,z,t}Rs+1:s=br(C)[Un+=Um,Uk]

{x,y,z,t}Rs+1:s=br(C)[Vn+=Vm,Vk]

{x,y,z,t}Rs+1:s=br(C)[Wn+=Wm,Wk]

指令中的br前缀代表位反序寻址，前缀br后的立即数C代表位反序的位数，它决定了指令中的哪些位元需要反序。例如指令br(7)[U0+=U1,U2]=R1:0，反序控制参数值为7，表明将地址的[7:0]位进行反序操作。它产生的4 对地址是：[反序(U0)]、[反序(U0)+1]；[反序(U0)+2×U2]、[反序(U0)+2×U2+1]；[反序(U0)+2×2×U2]、[反序(U0)+2×2×U2+1]；[反序(U0)+3×2×U2]、[反序(U0)+3×2×U2+1]。4对地址所取得的数据依次存放到4个执行核X/Y/Z/T的R1和R0中去。而基地址寄存器U0 将被修改为[U0+U1] ，用不反序的U0 值进行基地址的自增。

可以看出，若U2设置为1，则指令所涉及到的4对地址连续，可以保证分布在8个独立存储器中，不会发生地址冲突。如果限制输入数据地址为8的边界(即低3位为000)，再将增量U1设置为8，则连续的4对取数地址可以等效为FFT逆序数的最低2 bit单独进行逆序交换的逆序循环，如图4所示。

图4 最低2 bit单独逆序交换取数图

图中*号表示任意取值。可以看出，将s的最低2 bit转化为地址基址U0后，采用4组地址发生器即可实现对所有逆序地址的连续内存访问，完全规避了地址冲突的风险。完成核间数据交换后，就可以得到正确顺序的处理结果。根据逆序循环原理，该处理结果同样占据输出地址空间的4段连续内存，保证了输出存储时的数据带宽。需要注意的是，由于复数占据了2个地址，因此实际逆序地址计算中逆序位数为FFT阶次n加2。要求输入FFT数据地址的第n+1位必须为0以保证取数首址的正确。

在编程实现时发现，由于在这种三级/四级合并的编程中，已经尽可能地发挥了BWDSP100的处理能力，再加入核间数据交换操作，其单个周期的并发指令数、ALU资源等都将成为瓶颈。而如果为此增加额外指令周期则影响了程序效率。

仔细研究图2所示算法架构，可以看出：在后面的处理中，除最后两级外，其余各级顺序读入的4个运算核的数据刚好分处在4个不同的FFT组内。各组旋转因子完全相同，运算步骤完全相同，编程十分方便。最后两级中可以进行高两位和低两位的逆序交换，从而完成整个逆序操作。由于最后两级BWDSP100的运算任务并不饱满(芯片支持单周期完成8次加减法实际只需要6次加减法)，这种交换操作可以在不影响效率的前提下插入原程序中运行，问题得到了圆满的解决。由于需要最后两级完成交换操作，程序能够实现的最小FFT点数为32点，基本可以满足工程实现需要。

3.3 提高程序的通用性

FFT运算所需要的位反序位数由FFT的长度决定。设FFT长度N为2的n次阶，则FFT运算所需的位反序位数为n，如果考虑到复数占据了2个地址，则BWDSP100位反序取数指令中位反序的位数需要设置为n+2。前面指出，BWDSP100的位反序取数指令中位反序的位数为固定常数，这就意味着一种FFT位反序只能处理对应点数的FFT。如果在实际应用中需要多种长度的FFT，就需要配备多种位反序操作。这样既增大了程序体积也降低了程序效率。

记原序数s的二进制表现形式为(Sn-1Sn-2…S0)，如果对其尾部添加m个零，记为s*(Sn-1Sn-2…S00m-1…0100)，则其对应的逆序数S*为(0001…0m-1S0S1…Sn-1)。可以看出，对新的原序数s*进行n+mbit位反序后得到的新的逆序数S*与原来的逆序数S数值相等。采用这样的办法，可以将原本位数不同的位反转操作统一扩充到固定点数，对应需要修改的是原序数的递增量。而BWDSP100指令中该递增量是可变的。设新的固定位反转位数为n+m，则新的递增量由原来的20改变为2m。BWDSP100芯片内部数据地址空间分配如图5所示。

图5 BWDSP100内部数据地址空间分配

从图5可以看出，BWDSP100内部数据Cache分为了3块，每块256K字。从地址角度看共18 bit。对于位反序取数指令{x,y,z,t}Rs+1:s=br(C)[Un+=Um,Uk]，Uk取1，固定位反序位数C应该取17。考虑到一个复数数据需占有2个字地址空间，Um的值应该为2(17-r)，式中r为FFT阶数。

由于芯片内部有X/Y/Z/T 4个运算核，所取数据将分落到这4个核中，为避免在前面的四级合并中因逆序而进行数据交换，考虑保留前后各2 bit地址到最后交换。将此2 bit考虑后，Um的值为2(19-r)。

这样修改后，新的程序可以适应各种2的整数次幂FFT处理。同时，由于对原序数尾部添0，逆序数对应头部填充了多个0，而BWDSP100指令中直接将计算得到的逆序数作为取数地址，因此带来的限制是输入FFT数据必须放在3个内部数据块的某一首地址。在实际工程应用中，这个限制条件对于可以进行绝对地址操作的BWDSP100而言比较容易实现。

4 测试结果

程序编制完成后，在BWDSP100评估板上进行了基于硬件的实际性能测试，与TS201芯片比较结果如表2所示。

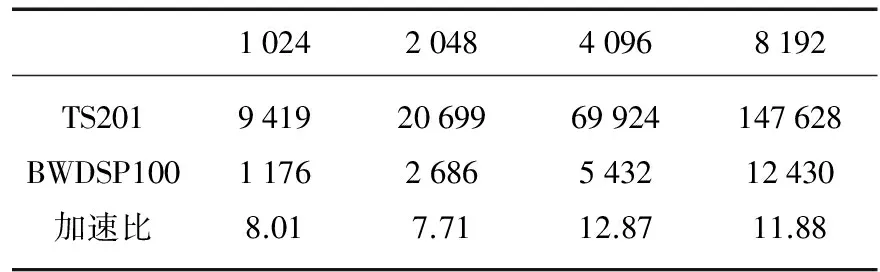
表2 BWDSP100与TS201 复数FFT周期数比较

从表2可以看出，BWDSP100的1 024点FFT性能达到TS201的8倍，满足原设计指标。2 048点FFT由于程序前端只进行了三阶合并，性能有所下降。从4 096点开始，BWDSP100采用SRAM的优势开始体现，较TS201性能有了较大的提升。

5 结束语

基于BWDSP100硬件特点，本文有针对性地给出了FFT算法实现中遇到的问题及解决办法。与国际成熟的DSP相比，最终FFT性能达到了设计理论要求。尽管本文基于特定平台，但文中给出的方法对BWDSP100应用及其他芯片FFT实现均有一定的参考作用。

[1] 袁琪,杨康,周建江,等. 大点数FFT算法C6678多核DSP的并行实现[J]. 电子测量技术, 2015, 38(2):74-80.

[2] 张杰,顾乃杰,张明. 龙芯3B处理器上FFT算法向量化研究[J]. 小型微型计算机系统, 2015, 36(7):1639-1643.

[3] 史鸿声,穆文争,刘丽. 基于“魂芯一号”的雷达信号处理机设计[J]. 雷达科学与技术, 2012, 10(2):161-164.

SHI Hongsheng, MU Wenzheng, LIU Li. Design of Radar Signal Processor Based on HunXin-1 Chip[J]. Radar Science and Technology, 2012, 10(2):161-164.(in Chinese)

[4] 许德刚. 基于BWDSP100处理器的无源雷达信号处理系统[J]. 舰船电子对抗, 2015, 38(2):72-75.

[5] 贾光帅,洪一,刘小明,等. 基于“魂芯一号”的自适应截位浮点乘法实现[J]. 雷达科学与技术, 2015, 13(3):324-327.

JIA Guangshuai, HONG Yi, LIU Xiaoming, et al. Implementation of Adaptive Truncation of Floating-Point Multiplier Based on BWDSP100 Processor[J]. Radar Science and Technology, 2015, 13(3):324-327.(in Chinese)

[6] 方志红,张长耀. 逆序循环在原位FFT中的应用[C]∥全国第21届计算机技术与应用学术会议, 合肥:中国科学技术大学出版社, 2010:43-46.

[7] 方志红,张长耀,俞根苗. 利用逆序循环实现FFT运算中倒序算法的优化[J]. 信号处理, 2004, 20(5):533-535.