阵元失效条件下MIMO雷达成像方法研究

， ， ， 2,

(1.南京信息工程大学气象灾害预报预警与评估协同创新中心， 江苏南京 210044；2.南京信息工程大学江苏省气象探测与信息处理重点实验室， 江苏南京 210044；3.南京信息工程大学电子与信息工程学院， 江苏南京 210044)

0 引言

多输入多输出(Multiple Input Multiple Output, MIMO)雷达作为一种新体制雷达技术，最近受到科研人员的广泛关注和研究。与传统的相控阵雷达相比，MIMO雷达能显著提高参数的可识别能力和角分辨率，提高波束设计的灵活性，具有更优的目标检测性能和参数估计性能[1]，而且还可通过虚拟天线扩展阵列孔径，提升目标可识别数目的上限[2]。

近年来，压缩感知(Compressed Sensing, CS)[3-4]理论广泛应用于MIMO雷达成像。在实际雷达探测场景中，目标个数仅占据少量的分辨单元，则MIMO雷达接收到的回波信号是稀疏的，因此可以使用CS理论解决MIMO雷达的成像问题。文献[5]建立了加权lq范数最小化的MIMO雷达成像模型，并利用迭代方法重构出较高精度的目标三维像。为了提高MIMO雷达成像的实时性，文献[6]研究了基于SL0算法的MIMO雷达成像方法，该方法利用更加陡峭的双曲正切函数来逼近l0范数，并采用修正牛顿法求解近似l0范数最小化问题，提高了MIMO雷达的成像精度和速度。

为了提高成像质量，MIMO雷达一般采用较大的信号带宽以提高目标的距离分辨率，此时传统均匀采样需要较高的采样速度，而数据存储速度与采样速度又相差近100倍，巨大的速度不匹配会导致数据溢出丢失，影响雷达系统的整体性能，因此均匀采样对雷达系统的硬件要求很高。为了降低MIMO雷达的硬件实现难度，文献[7]通过非均匀采样方式获得 MIMO雷达的回波信号矩阵，并证明了该矩阵满足低秩性，即该矩阵的特征值具有稀疏特性，然后利用矩阵填充(Matrix Completion, MC)技术将非均匀采样的回波矩阵恢复成完整的均匀采样数据矩阵。在实际环境中，由于恶劣的自然环境、人为的干扰和硬件的使用寿命等众多影响，可能会出现MIMO雷达的部分接收天线关闭或损坏，已关闭或损坏的接收阵列天线将无法获得目标回波数据，这种情况定义为阵元失效。在阵元失效情况下，接收天线输出信号为零，此时MIMO雷达回波信号矩阵中对应失效阵元位置处存在整行元素的丢失情况即整行元素为零，从而导致信号矩阵不再具有强不相干性[8]。因此无法利用矩阵填充技术将非均匀采样的数据恢复成完整的均匀采样数据，导致MIMO雷达成像存在一定程度的恶化。

本文首先在MIMO雷达回波信号矩阵中对应失效阵元位置处的行元素上叠加微小的服从高斯分布的随机扰动量，使其能满足矩阵填充条件，再利用矩阵填充技术将非均匀采样的MIMO雷达回波数据矩阵恢复成完整的均匀采样数据矩阵，然后利用迭代加权lq最小化方法估计出目标场景向量。由于对失效阵元的回波数据未能有效利用，因此目标场景向量估计值存在较大的误差，影响MIMO雷达的三维成像质量。为了进一步提高目标场景向量的重构精度，利用已获得的目标场景向量粗估计值和感知矩阵重构出失效阵元的目标回波数据，再次利用矩阵填充和迭代加权lq最小化方法获得更接近最佳稀疏度的目标场景向量估计值，从而解决了阵元失效条件下的MIMO雷达成像问题。

1 阵元失效条件下非均匀采样MIMO雷达信号模型

m=1,…,Mt,h=1,…,H

(1)

d(ωh)=[1,ejωh,…,ej(L-1)ωh]T,h=1,…,H

(2)

式中，⊙为Hadamard积。则多普勒频移信号矩阵可表示为

(3)

(4)

PΩ(Y) =PΩ(YS)

(5)

式中，PΩ为投影算子，定义为

(6)

假设MIMO雷达出现r个接收天线关闭或损坏，它们的位置序号分别为n1,n2,…,nr，则在非均匀采样回波矩阵YS中存在r行与失效阵元位置相对应的行元素全为零，即

YS(ni,∶)=01×(L+P-1)，i=1,2,…,r

(7)

2 基于失效阵元丢失数据重构的MIMO雷达成像方法

由于MIMO雷达的非均匀采样回波矩阵YS存在整行元素为零的情况，即YS不再具有强不相干性，因此无法利用矩阵填充将非均匀采样的YS恢复成完整的均匀采样数据Y。为此，在矩阵YS中对应失效阵元位置处的行元素上叠加微小的服从高斯分布的随机扰动量，使其能满足矩阵填充条件，即

(8)

(9)

由于矩阵的秩函数是非凸的、非连续的，直接求解秩最小化问题比较困难，因此一般利用核范数最小化方法代替秩最小化方法来求解矩阵填充问题[10]，即可将式(9)转换成凸优化问题：

(10)

式中，‖·‖*表示矩阵的核范数，其值等于矩阵的奇异值之和。

A= [v1,1,1,v1,1,2,…,vP,K,H]

(11)

α= [α1,1,1,α1,1,2,…,αP,K,H]T

(12)

y≈Aα+n

(13)

式中，n=vec(N)。

本文采用迭代加权lq最小化算法[5]来估计MIMO雷达目标场景向量，通过求解式(14)的目标函数可获得目标场景向量α的估计值：

(14)

(15)

(16)

将接收信号矢量yR按向量矩阵化运算改写成矩阵形式，即

(17)

由式(17)可知，在重构矩阵YR中失效接收阵元位置所对应行数据可认为是失效阵元所丢失的目标回波数据，提取矩阵YR中的这些行数据并替换MIMO雷达的接收信号矩阵YS中相同位置的行数据，即可恢复出失效阵元的目标接收数据：

(18)

3 仿真与分析

为了验证本文方法在阵元失效条件下MIMO雷达成像方面的优势，本文设计了利用迭代加权lq方法、MC-lq方法和本文方法进行MIMO雷达成像的对比实验，其中，迭代加权lq方法表示直接采用迭代加权lq方法对阵元失效条件下的非均匀采样MIMO雷达回波信号中估计出目标场景向量； MC-lq方法表示先利用矩阵填充技术将非均匀采样的MIMO雷达回波数据矩阵恢复成完整的均匀采样数据矩阵，再利用迭代加权lq方法估计出目标场景向量。

仿真参数设置：MIMO雷达系统的发射天线个数Mt=5，接收天线个数Mr=25，天线阵列按均匀线阵布置，发射天线间隔dt=2.5λ0，接收天线间隔dr=0.5λ0；发射信号选取噪声调频信号[11]，发射波形的采样个数L=32；回波噪声选取均值为零、方差为σ2的加性高斯白噪声，回波信噪比定义为

(19)

式中， tr(·)表示求矩阵的迹。目标场景的距离单元数P=12；雷达扫描的角度范围[-30°，30°]，角度划分间隔为1°，则划分后的角度单元数K=61；目标的多普勒频移用角度表示，即Φh=

定义重构信噪比如下：

(20)

仿真1： MIMO雷达距离-角度-多普勒成像

图1为MIMO雷达在多普勒单元5°处的距离-角度成像，其中，图1(a)为真实目标的距离-角度分辨单元分布，图1(b)、(c)和(d)分别为利用迭代加权lq方法、MC-lq方法和本文方法估计获得的目标距离-角度成像图，其中回波信噪比为20 dB，采样率N=0.85。由图1可知，由于回波信号存在采样数据和失效阵元数据丢失情况，迭代加权lq方法的距离-角度成像旁瓣电平较高，而且在真实目标附近存在许多虚假目标，导致目标的距离-角度成像质量下降比较严重；MC-lq方法利用矩阵填充方法能将非均匀采样数据恢复成完整的均匀采样数据，因此其成像旁瓣电平要低于迭代加权lq方法，然而该方法对失效阵元的回波数据未能有效利用，导致该方法的目标距离-角度像仍然出现较大偏差；本文方法能够以较高的精度估计出目标的距离和角度信息，从而能获得高质量目标像。

(a)真实目标场景

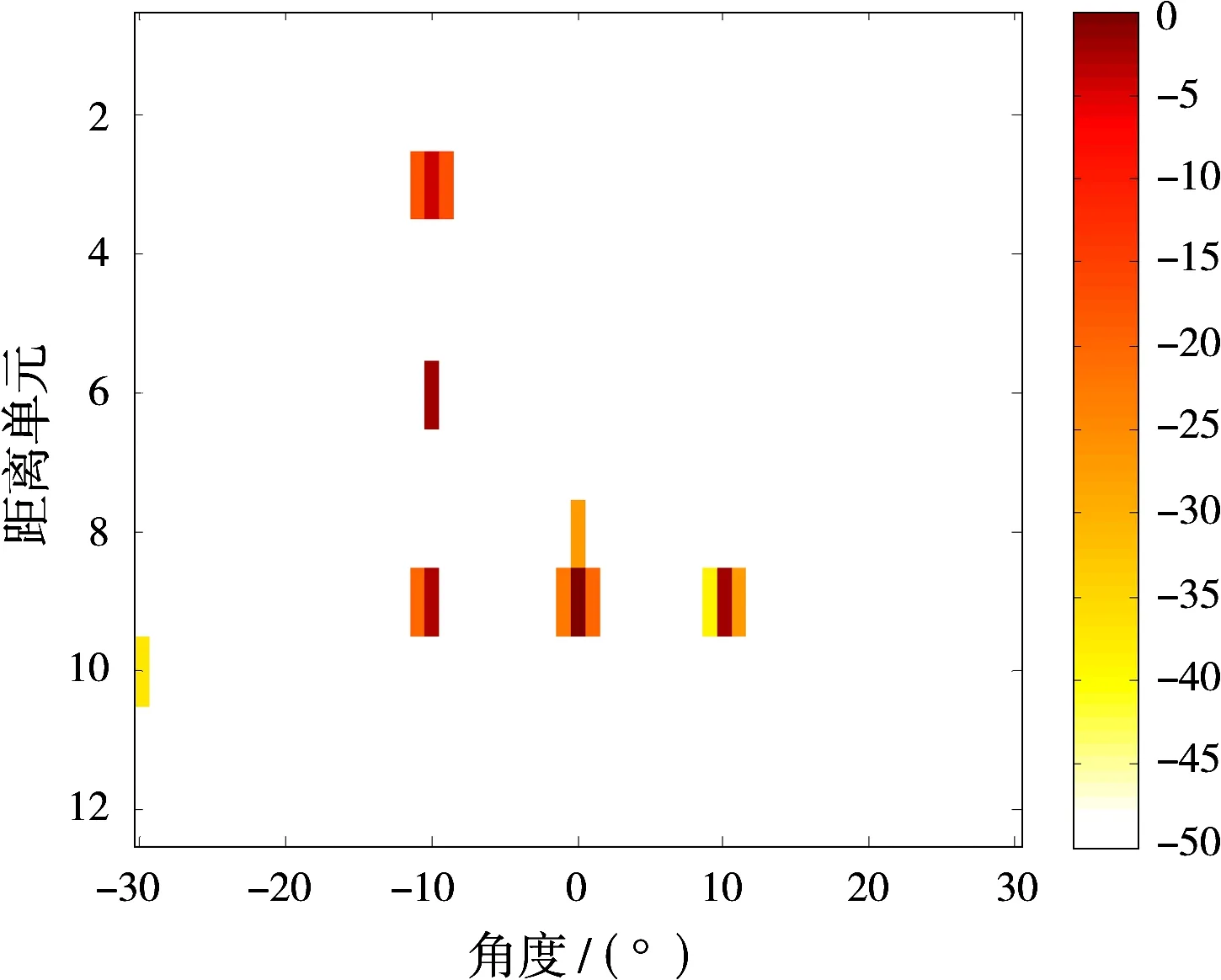
(b)迭代加权lq方法估计

(c)MC-lq方法估计

(d)本文方法估计 图13种方法在采样率N=0.85时距离-角度成像结果

图2为MIMO雷达在角度单元-10°处的距离-多普勒成像图，其中，图2(a)是真实目标的距离-多普勒分辨单元分布；图2(b)、(c)和(d)分别为采用迭代加权lq方法、MC-lq方法和本文方法获得的目标距离-多普勒成像结果图，其中回波信噪比为20 dB，采样率N=0.85。由图2可知，相比于迭代加权lq方法和MC-lq方法，本文方法能有效恢复出丢失的采样数据和失效阵元数据，从而能有效地重构出具有较高精度的目标距离和多普勒二维像，并与真实目标场景基本保持一致。

(a)真实目标场景

(b)迭代加权lq方法估计

(c)MC-lq方法估计

(d)本文方法估计 图23种方法在采样率N=0.85时距离-多普勒成像结果

仿真2： 3种方法的重构信噪比与采样率的变化关系

选取回波采样率在0.5～1之间均匀变化，回波信噪比SNR=20 dB，重复100次蒙特卡洛实验。图3为3种方法的重构信噪比与回波信号采样率的变化关系。由图3可知，本文方法对目标场景向量的重构信噪比明显高于迭代加权lq方法和MC-lq方法；MC-lq方法的重构信噪比在采样率N=0.6后就趋于稳定，这是由于当回波采样率大于0.6时，矩阵填充方法就能成功将非均匀数据恢复成完整的均匀采样数据；当采样率N=1即此时MIMO雷达的回波信号表现为完整的均匀采样数据时，由图3可知MC-lq方法和迭代加权lq方法具有类似的重构信噪比，但是由于它们未充分利用失效阵元的丢失数据，致使目标场景向量的重构性能仍然劣于本文方法。

图3 当SNR=20 dB时3种方法的重构信噪比与采样率的变化关系

仿真3： 3种方法的重构信噪比与回波信噪比的变化关系

选取回波信噪比在0～25 dB之间变化，回波信号采样率N=0.85，重复100次蒙特卡洛实验。图4为3种方法的重构信噪比与回波信噪比的变化关系。由图4可知，虽然在低回波信噪比下本文方法的目标场景向量误差与MC-lq方法和迭代加权lq方法相差不大，但是随着回波信噪比的增加，本文方法能凭借所恢复的失效阵元所丢失的目标数据，从而使其重构信噪比远优于MC-lq方法和迭代加权lq方法，能以较高的精度重构出目标的距离-角度-多普勒三维像。

图4 当采样率N=0.85时3种方法的重构信噪比与回波信噪比的变化关系

4 结束语

MIMO雷达的天线阵列在实际使用中不可避免地存在由于器件老化及物理损坏等因素而出现阵元失效情况。由于失效天线阵元在整个接收时间内输出信号为零，因此MIMO雷达接收信号矩阵中存在整行元素丢失现象，从而导致目标成像质量恶化。本文在失效阵元输出的整行或整列零元素上叠加微小的服从高斯分布的随机扰动量，使其能满足矩阵填充条件，并利用矩阵填充和迭代加权lq方法获得目标场景向量粗估计值，然后根据目标场景向量粗估计值和感知矩阵重构出失效阵元的目标接收数据，从而能以较高程度重构了目标的三维像。该方法解决了失效阵元对目标场景重建存在一定程度偏差的问题，提高了目标成像质量，保证在不更换已损坏接收天线的情况下，仍然使得MIMO雷达成像系统正常工作，在一些维修不便或者耗资庞大的场合发挥重要作用，具有重要的军事意义。

[1] XU J, LIAO G, ZHU S, et al. Joint Range and Angle Estimation Using MIMO Radar with Frequency Diverse Array[J]. IEEE Trans on Signal Processing, 2015, 63(13):3396-3410.

[2] 窦道祥,李茂,何子述. 单基地MIMO雷达降维Power-ESPRIT算法[J]. 雷达科学与技术, 2015, 13(1):76-80, 85.

[3] DONOHO D L. Compressed Sensing[J]. IEEE Trans on Information Theory, 2006, 52(4):1289-1306.

[4] CANDES E J, WAKIN M B. An Introduction to Compressive Sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2):21-30.

[5] GONG Pengcheng, SHAO Zhenhai. Target Estimation by Iterative ReweightedlqMinimization for MIMO Radar[J]. Signal Processing, 2014, 101(C):35-41.

[6] FENG J J, ZHANG G, WEN F Q. MIMO Radar Imaging Based on Smoothedl0Norm[J]. Mathematical Problems in Engineering, 2015, 2015(1):1-10.

[7] SUN S, BAJWA W U, PETROPULU A P. MIMO-MC Radar:A MIMO Radar Approach Based on Matrix Completion[J]. IEEE Trans on Aerospace and Electronic Systems, 2015, 51(3):1839-1852.

[8] CANDES E J, PLAN Y. Matrix Completion with Noise[J]. Proceedings of the IEEE, 2009, 98(6):925-936.

[9] CANDES E J, TAO T. The Power of Convex Relaxation:Near-Optimal Matrix Completion[J]. IEEE Trans on Information Theory, 2010, 56(5):2053-2080.

[10] CAI J F, CANDES E J, SHEN Z. A Singular Value Thresholding Algorithm for Matrix Completion[J].SIAM Journal on Optimization, 2008, 20(4):1956-1982.

[11] 王超宇,贺亚鹏, 胡恒,等. 基于贝叶斯压缩感知的噪声MIMO雷达目标成像[J]. 南京理工大学学报, 2013,37(2):262-268.