几何直观

麻炳铃

[摘 要]几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。在教学上，通过引导学生对比多种方法，挖掘几何直观内涵，培养学生的几何直观能力。

[关键词]几何直观 解决问题 能力培养

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2016）05-076

《义务教育数学课程标准（2011年版）》指出：“借助几何直观可以把复杂的数学问题变得简明、形象，有助于学生梳理探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。”而在实际教学中，部分教师在认识上存在着一定的局限性，在课堂教学中，仅仅重视培养逻辑推理能力，忽视对学生几何直观能力的培养。因此，全面地理解几何教育的价值，重视几何直观，使学生能够灵活地运用“以形助数”这把“利剑”，巧妙地解决复杂的数学问题，真正有效地提高学生的几何直观能力，这应是一线教师努力的方向。

一、巧用对比，感受几何直观价值

心理学家皮亚杰根据儿童的认知理论将儿童的认知分为四个阶段：感知运动阶段、前运算阶段、具体运算阶段、形式运算阶段。而小学阶段的学生正处于第三阶段，他们很难理解复杂的数量关系，如果能借助图形使数量关系直观化、形象化、简单化，那么找到解题的方法相对也较容易。要想让学生主动地以形助数，首先应该让其感受几何直观的内在价值，激起他们内在的驱动力。这就要求教师在平时的教学中选择合适的教学内容，引导学生感受和领悟图形的价值。

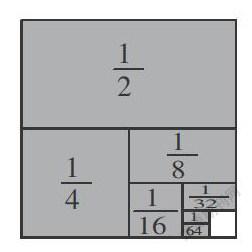
例如，计算“+++++”时，大部分学生用通分的方法，比较繁琐。这时教师就可引导学生观察图1，轻松得出“要求‘+++++’的和，其实就是要求出图中所有阴影部分的面积之和，而‘图中所有阴影部分的面积=1-空白部分的面积’，空白部分的面积其实等于最后一个加数的大小，即，所以+++++=1-=”。

通过对比方法，借助图形的直观性特点将抽象的数转化成直观的图形，在“形”与“数”的对应中，将一道复杂的运算转化成求图形的阴影部分面积，不仅降低了运算的难度，加深了学生对数的意义的理解，同时也为学生对算理的理解打开了一条新的通道。这样的学习过程不仅能让学生感受到豁然开朗的轻松愉悦，也能让学生萌发主动应用几何直观的意识。

二、适时操作，积累几何直观经验

直观，虽然没有经过严格的逻辑推理，却能有效促进人们对观察对象的全貌和本质的把握。借助几何图形的直观，常常能发现图形之间的关系，甚至会产生对相关数量之间关系的猜想。正如“语感”、“数感”那样，学生也只有在平时的动手操作中不断地积累，才能逐步提高几何直观素养。

例如，新北师版四年级下册“优化”的教学片断。

师：要想尽快吃上饼，至少需要多长时间？

生1：只要12分钟。

生2：只要9分钟。

师：看来大家有不同的意见。请把老师提供的圆形纸片当做饼，先模拟一下烙饼过程，再把你的想法在课堂作业本上表示出来。（生迫不及待地开始动手操作）

师：谁来说说你是怎么烙饼的？

生3：假设数学书是“锅底”，这三张圆形纸片是三个“饼”。我是先烙第一个饼的正面和第二个饼的正面，再烙第一个饼的反面和第二个饼的反面，接着烙第三个饼的正面，最后烙第三个饼的反面。所以共需要3×4=12（分钟）。

生4：我是用圆形纸片表示饼，第一次先烙第一个饼的正面和第二个饼的正面，第二次烙第一个饼的反面和第三个饼的正面，第三次烙第二个饼的反面和第三个饼的反面。所以只要3×3=9（分钟）。

师：为什么生4比生3所用的时间少呢？

生5：因为生3在第三次和第四次烙饼的时候，没有同时烙两个饼，浪费了空间。

师：生4所用的时间会是最少的吗？

生6：会，因为它每次都烙两个饼，没有浪费空间。

……

在操作中，学生用圆形纸片替代饼，再将圆形纸片抽象成圆形符号，经历了“实物直观→替代物直观→符号直观”的抽象过程。正因为借助直观图形，并动手操作，学生才能轻而易举地把烙饼过程抽象成图形符号和数学语言，学生既明白了怎样烙饼才能更省时间的道理，抽象思维又得到了发展，在一定程度上积累了几何直观经验。

三、挖掘本质，凸显几何直观内涵

运用几何直观研究问题，通常要先把研究的“对象”抽象成“图形”，再把“对象之间的关系”转化为“图形之间的关系”，从而把所研究的问题转化为关于“图形的数量或位置关系”的问题，然后借助图形进行思考、分析，从而找到解题思路。因此，教师应在培养学生利用几何直观描述与分析问题的意识与能力上下工夫，这就意味着，对几何直观的教学，教师要关注学生表述问题的过程，以及表述之后的反思与顿悟。没有反思与顿悟，学生可能获得了几何的方法，却未必获得“几何直观”的能力。

例如，教学“3的倍数特征”时，大多数教师都采用“先让学生在100以内的数表中圈出是3的倍数的数，然后引导学生观察这些数有哪些共同特点，进而探索出3的倍数特征——各个数位上的数字的和是3的倍数”。这样的课给人感觉缺少一点“深度”，即对“3的倍数特征本质”的挖掘。教师不妨再追问学生两个问题——

师：为什么3的倍数的特征是各个数位上的数字的和呢？（生表示疑惑）。

师：我们用小棒数量来表示数43（4捆小棒加3根小棒），每捆小棒都有10根，3根3根地分，每捆还剩下几根？

生1：还剩下1根。

师：这样4捆共剩下几根？

生2：4根。

师：这时只要把这4根小棒再加上个位上的3根小棒，所以要看43是不是3的倍数只要看十位数字与个位数字的和。

师（再次追问）：如果这个数是三位数，你能解释其中的道理吗？

生3：也是一样的道理。百位上的数字如果是“6”，表示600根，每100根一捆，3根3根地分以后，也还是剩下1根，6捆总共剩下6根，所以只要用百位上的数字“6”加十位上的数字和个位上的数字，即各个数位上的数字的和。

师：这位同学条理非常清楚，相信同学们也能用同样的方法解释更大的数。

通过追问学生两个数学问题：“为什么3的倍数的特征是各个数位上的数字的和？”和“如果这个数是三位数，你能解释其中的道理吗？”进一步激发学生进行数学思考。学生借助直观的小棒，能够发现：“4捆小棒就是表示十位数中的40，单独的3根小棒表示个位的数字3。紧接着要判断是不是3的倍数只要看每捆中剩下的小棒与单独小棒的总数之和。”学生不仅知其然，还能知其所以然，在观察、分析中学生的几何直观能力得到了提升。

“冰冻三尺，非一日之寒。”培养学生的几何直观能力同样需要一个长期、循序渐进的过程，需要教师在教学中长期关注，有意识地渗透，不断地将学生的思维引向深处，真正提高学生的几何直观能力。

（责编 童 夏）