多尺度内聚模型颗粒群振动挤压破碎数值模拟研究

郭进山，祁步春，蔡改贫，夏刘洋，曾艳祥

（江西理工大学 机电工程学院，江西 赣州 341000）

多尺度内聚模型颗粒群振动挤压破碎数值模拟研究

郭进山，祁步春，蔡改贫，夏刘洋，曾艳祥

（江西理工大学 机电工程学院，江西 赣州 341000）

不规则钨矿石颗粒的破碎特性是离心选矿机设计的重要依据，本研究通过对不同几何形状的结构及内聚力多尺度两个方面构建不同形状的矿石颗粒群模型，利用EDEM进行颗粒群在振动及无振动条件下的数值模拟试验，分别对颗粒群模型在振动及无振动条件下的挤压破碎效果进行对比分析，并分析颗粒群的破碎特性及力学分布特性。研究结果表明：在一定振动参数下颗粒群的破碎率均高于无振动情况，并且随着振幅的增加，在不同频率下模型破碎率大体上呈增加趋势；对比无振动条件下模型破碎率，表明振动参数有利于颗粒群模型的破碎。

多尺度；内聚力；颗粒群；振动挤压；破碎率

矿石实际是由大量细观颗粒及内部孔隙组成，颗粒与颗粒之间存在的胶结物质将颗粒聚合成一个整体。其破碎特性是离心选矿机研究的重要参数。

基于离散单元法引入颗粒材料的多尺度模型[1]，其核心就是细观尺度的团簇，Plesha等[2]针对复杂形状颗粒体提出了颗粒簇的概念。Mcdowell等[3]建立了等边直角三角形颗粒模型，使断裂后的等边直角三角形可进行进一步断裂。该模型的缺点在于无法模拟矿石颗粒间的孔隙特点，但这种断裂思想值得借鉴。楚锡华等[4]在分析土体颗粒破碎的力学机理和工程效应时，通过引入多尺度分级模型，定义不同尺度的基本颗粒和颗粒簇，建立了可模拟颗粒破碎的多尺度分级离散颗粒模型来模拟颗粒破碎过程。黄俊宇等[5-6]基于离散元方法（DEM）构建脆性颗粒材料多尺度模型，对多尺度模型所涉及的两种接触模型和两种黏结模型的参数进行分析。内聚力区域最早的模型由Dugdale提出[7]。此理论在模拟脆性材料的断裂、韧性材料的动态断裂和破碎、混凝土的动态Bazilina测试等方面均有显著效果[8-11]。

本研究对，某钨矿石破碎形状进行统计分析，其中大部分为不规则碎片颗粒，其形状为类圆形、类梯形、类菱形与类三角形，并通过对不同几何形状的结构描述及内聚力多尺度两个方面构建不同形状的矿石颗粒群模型，利用EDEM进行颗粒群在振动及无振动条件下的数值模拟试验，分别对颗粒群模型在振动及无振动条件下的挤压破碎过程进行描述，并分析颗粒群的破碎特性及力学分布特性，为钨矿石颗粒群的破碎机理及振动下的破碎特性提供一定的理论依据。

1 多尺度内聚力模型构建

1.1 不同几何形状多尺度结构构建

结构体的形状并非单一，参考实际矿石形状并结合颗粒簇之间的接触类型可构成不同形式三级结构体颗粒模型，试验以三角形、四边形（菱形）以及圆形为例进行多尺度颗粒模型构建描述。其中，类三角形多尺度模型部分典型结构示意图如图1所示。

图1为三角形形状的多尺度颗粒模型结构图。其中模型T1为单点连接模式结构图，可表示成3A；模型T2为两点三角连接与两点平行连接模型组合构成的结构图，可表示成2B+C；模型T3为两点平行连接模型结构图，可表示为3C。

类菱形多尺度模型部分结构如图2所示。图2为菱形结构多尺度颗粒模型图。同样，模型R1可表示为5A；模型R2表示为5C；模型R3表示为3C+ 2B；模型R4表示为2C+3B；模型R5则表示为C+4B。从构成形式上，模型R1、R2为各向同性体，模型R3、R4、R5则表现为各向异性。

图1 三角形颗粒多尺度结构模型图Fig.1 Multi-scale structure model of triangular particles

图2 菱形颗粒多尺度结构模型图Fig.2 Multi-scale structure model of diamond particles

在由4个颗粒簇构成的菱形结构颗粒模型基础上，增加3个颗粒簇，形成“6+1”结构类圆形颗粒结构体。此时，一级颗粒簇与二级颗粒簇在结构上达到了统一，“6+1”结构类圆形结构体同样以“6+1”结构的颗粒簇进行替换，其典型结构如图3所示。

图3 类圆形颗粒多尺度结构模型图Fig.3 Multi-scale structure model of circular particles

如图3所示，类圆形多尺度模型有以上10种典型组合方式，其中模型C1～C6表示单点连接模式向两点连接模式的依次转换，6种结构模型的连接方式由最初的12A转换为6B+6C，通过增加两点连接个数减少单点连接来减小模型整体的内部孔隙，从而达到致密的模型结构，如模型C6所示。模型C7与模型C6内部孔隙相同，而模型C7在结构上为全两点平行接触，结构上表现为各向同性。由于增加B类型的连接有助于减小模型内部孔隙，则可构建模型C7的变形体C8、C9、C10，其内部孔隙依次减小，模型C10达到“6+1”形式结构体最致密填充。

综上所述，以“6+1”结构颗粒簇作为多尺度模型基本结构能很好地形成多种结构的颗粒宏观结构体，具体表现在：一是能最大程度上保证原始圆形颗粒结构体的几何形状；二是能形成较低的内部孔隙，能体现岩石致密性特点。

1.2 多尺度结构的内聚力定义

颗粒模型中最基本单元为一级颗粒，同时也是离散元模拟中最基本的元素。一级颗粒为刚性不可破颗粒，即粒子本身不能发生变形及破坏。由于有最小粒子的限制，使得模型在模拟破碎方面具有缺陷。一般而言，模型所定义的最小粒子越小越能模拟真实颗粒破碎过程，但同时计算量会急剧增大，因此一级颗粒尺寸的选取应考虑到模型的计算量。本研究拟采用三级颗粒模型来定义内聚力。

2 颗粒群模型及试验方案

在离散元软件EDEM中，采用上述18种典型结构形状的多尺度内聚颗粒模型建立颗粒群破碎模型，如图4、图5所示。为了便于分析计算，在仿真中限制了颗粒在Y方向上的运动，因此只考虑颗粒在X-Z平面内的平移以及绕Y轴的转动。图中颗粒群模型中有3种形状的颗粒模型包含18种结构，每个类型有2个相同结构颗粒模型，共生成二级颗粒198个，一级颗粒1 386个，二级颗粒黏结键528个，一级颗粒黏结键2 376个，颗粒群模型中颗粒单元体半径为1.5 mm。

图4 颗粒群模型初始生成状态图Fig.4 Initial generating state diagram of particle swarm model

振动台位移方程设为余弦运动，其中振幅A为0.5mm、2mm与4mm；频率f为5Hz、20Hz和100Hz，进行全组合振动挤压仿真试验，试验共9组。9组试验均取底板压缩速率vc=20 mm/s进行振动挤压破碎仿真。同时进行无振动挤压破碎，对比施加振动与纯挤压下颗粒群模型的破碎效果的异同之处。

图5 颗粒群模型自重平衡状态图Fig.5 Self-weightequilibriumstatediagramofparticleswarmmodel

3 仿真结果分析

3.1 振动对颗粒群模型破碎效果对比分析与无振动

通过上述对施加振动及无振动条件下颗粒群模型破碎过程的描述可知，两种情况下颗粒群模型的破碎过程均体现了多尺度内聚颗粒模型的破碎特点。但是在处于相同压缩位移下，颗粒群模型中黏结键断裂分布情况有一定差别。统计颗粒群模型破碎率随压缩位移变化情况如图6所示。

图6 有无振动下破碎率随压缩位移变化Fig.6 Variation of crushing rate with the diversified compression displacementundertheconditionsofvibrationandwithoutvibration

图6中分别描绘了颗粒群模型在振动条件下（A=2 mm、f=5 Hz）与无振动条件下颗粒群模型整体破碎率随压缩位移的变化情况。观察图中两条曲线，可明显得出在压缩过程中，当振动板以A=2 mm、f= 5 Hz进行振动时的模型破碎率均高于无振动加载。并且，随着压缩位移的增加，模型破碎率间的差值整体呈增加趋势，在压缩位移为4 mm时的2%增加到压缩位移为32 mm时的20%左右。结果表明，在对颗粒群模型进行压缩的同时，对振动板施加A=2 mm、 f=5 Hz的振动加载有利于模型的破碎，使得模型具有更好的破碎效果。

3.2 振动参数对颗粒群破碎效果的影响分析

为了进一步分析振动参数对多尺度内聚颗粒模型颗粒群在振动挤压加载条件下的破碎效果，分别对不同振幅和频率组合下的颗粒群模型的破碎率随压缩位移的变化情况进行描点绘图，如图7、图8、图9所示。

图7 f=5 Hz不同振幅下破碎率随压缩位移变化Fig.7 Variationofcrushingratewiththediversifiedcompression displacementunderdifferentamplitude(f=5Hz)

图7中三条曲线由上到下分别为在频率为5Hz，振幅为4mm、2mm、0.5mm组合下颗粒群模型整体破碎率随压缩位移增加的变化情况。图中的每一节点表示一次碾压的结束，在频率取5Hz时振动板共振动8次。从图中可以明显看出，A=0.5mm、f=5Hz时的模型破碎率曲线与无振动时模型破碎率较为接近，并且最终破碎率相一致，表明在频率f=5 Hz下，取较低振幅A=0.5mm时，振动对颗粒群模型的破碎基本上无影响；随着振幅的增加，模型整体破碎效果越好，在振幅取4mm时，模型最终破碎率达到100%。

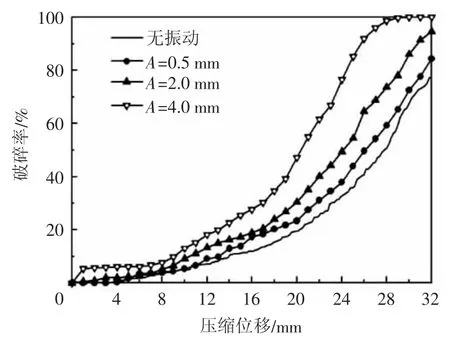
图8 f=20 Hz不同振幅下破碎率随压缩位移变化Fig.8 Variationofcrushingratewiththediversifiedcompression displacementunderdifferentamplitude(f=20Hz)

图8为频率增加到20 Hz，振幅为4 mm、2 mm、0.5 mm组合下的颗粒群模型破碎率随压缩位移变化情况，此时振动板在压缩位移32 mm内共振动30次。从图中可以看出，在相同压缩位移下随着振幅的增加，模型破碎率同样呈增加趋势；并且在振幅A= 4 mm下，当压缩位移达到28 mm时，模型破碎率就已达到100%。同样在较低振幅A=0.5 mm下，模型破碎率曲线与无振动破碎率曲线相差很小，模型最终破碎率相差4%左右。

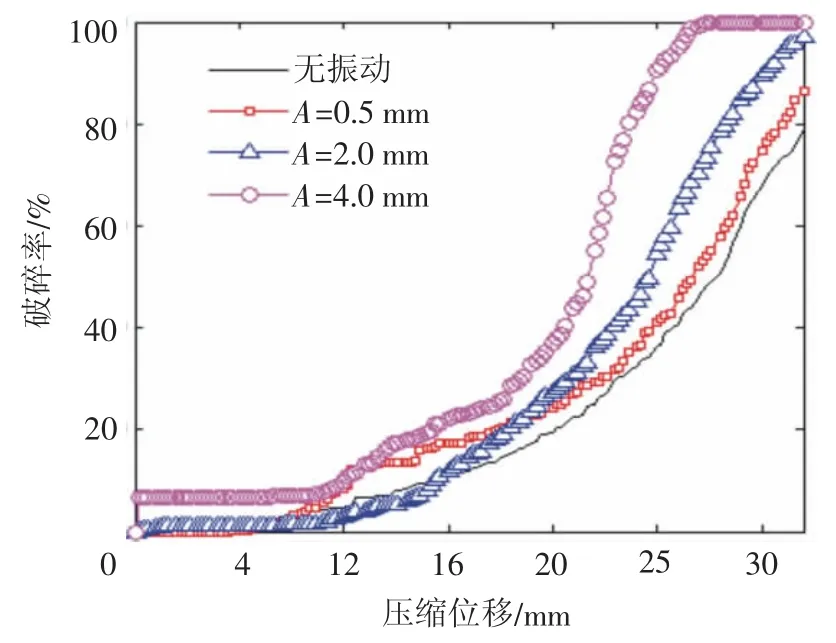
图9 f=100 Hz不同振幅下破碎率随压缩位移变化Fig.9 Variation of crushing rate with the diversified compression displacement under different amplitude(f=100 Hz)

图9为频率f取100 Hz下颗粒群破碎率随压缩位移变化情况。在该频率下，振动板共振动150次。观察图中曲线，在压缩位移小于8 mm情况下，在振幅为0.5 mm及2 mm时，模型破碎率接近0，几乎没有发生破碎；当振幅增加到4 mm时，模型破碎率从开始时刻瞬间增加到8%左右后保持不变。当压缩位移大于8 mm时，三组振动参数下模型的破碎率均开始增加。特别的，在压缩位移8～18mm内，振幅2 mm下模型破碎率低于振幅0.5 mm；在压缩位移18～32 mm内，振幅2 mm下模型破碎率却高于振幅0.5 mm下的模型破碎率，这是由于在压缩前期高频振幅振动下颗粒群随机排列后内部形成的强力链较多，颗粒群处于稳定状态，破碎较为困难，而高振幅下作用时间长能量聚集较大，这种稳定状态被打破发生破碎现象；低振幅或无振动条件下颗粒群排列幅度较小或无排列，颗粒群处于亚稳定状态，易发生破碎现象。在振幅为4 mm时，当压缩位移达到25 mm左右时，模型破碎率已达到100%。

通过观察图7～图9中曲线变化规律可大致得出以下结论：在压缩距离为15 mm以下时，颗粒群模型的破碎率随压缩距离的增加增长缓慢，当压缩距离大于15 mm时，颗粒群破碎率明显加快。这是由于在压缩距离小于15 mm之内，颗粒群主要发生三级颗粒的破碎，三级颗粒由于形状结构的非统一性，使得破碎为选择性破碎，又由于振动挤压的加载方式使得颗粒群整体结构发生重排，因此造就破碎率增长缓慢；然而当压缩距离大于15 mm后，破碎区域内部基本上全为二级颗粒，由于二级颗粒大小形状相同并且几乎布满整个破碎区域，因此在受到压缩时，二级颗粒成区域性发生破碎，造成颗粒群破碎率急剧增长；各频率下颗粒群模型的破碎率随着振幅的增加而增大，这是由于在振动挤压下颗粒群重新排列后更为密实，振幅越小作用时间越短，能量聚集较少，颗粒群未来得及破碎，故破碎率较低。

3.3 颗粒群力链演变过程分析

颗粒群模型由于其内部三级颗粒结构的非统一性，在进行振动挤压破碎时，三级颗粒之间发生碰撞形成力的传递，三级颗粒内部同样也存在力的传递现象。基于力链分布情况可对多尺度内聚颗粒模型颗粒群的振动挤压破碎过程进行描述。

图10为颗粒群在第一次碾压过程中颗粒受力情况，从图中可以看出，由于颗粒模型结构的不规则性，受到振动板挤压时，仅在破碎区域中间部位产生了较大压力，图中黑色颗粒表示颗粒受挤压力较大，灰色表示受挤压力较小。并且，模型受力集中于三级颗粒与三级颗粒之间的接触点处与三级颗粒和几何体接触处（图10中方框处所示），这是由于多尺度内聚颗粒模型在破碎前作为一个整体参与计算。因此，多尺度内聚颗粒模型颗粒群受到压缩时，首先在相互接触的三级颗粒之间产生压力，随后扩展到三级颗粒的内部，形成力的传递。

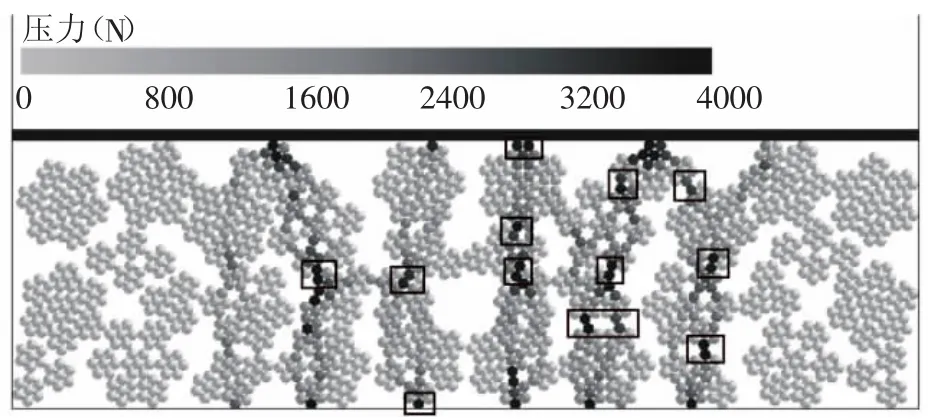
图10 颗粒群第一次压缩过程中颗粒受力云图Fig.10 Stress cloud images of the particles during the particle swarm's first compression

由图11展示了多尺度内聚颗粒群模型在振动挤压条件下，振动板每次压缩到最低点时模型内部黏结键形成力链的变化情况和碾压第一遍到第八遍多尺度内聚模型颗粒群所形成的力链分布。力链上的力具体表示为颗粒间黏结键上所受的法向力，键颜色的深浅表示键上力的强弱。

由图11可见，颗粒群模型受到压缩所产生的力链传递方向基本与外载荷（压缩）方向平行，图中黑色线段为压缩过程中形成的强力链，形成强力链的颗粒间具有较大变形，一般形成准直线，传递较大份额的挤压力；其他颗粒间的接触变弱，传递较小的挤压力，形成了弱力链，图中灰白色线段所示。

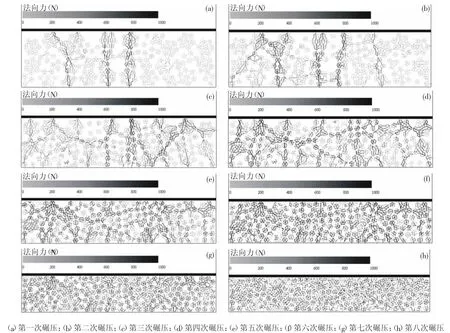
图11 颗粒群模型力链分布Fig.11 Force distribution of particle swarm model

如图11（a）和图11（b）所示，在挤压初期由于三级颗粒结构的非统一性，所形成强力链的数目一般较少，却支撑起颗粒体系的大部分挤压力，相对的弱力链数目则较多，几乎均匀分布于颗粒群体系中，对强力链形成辅助作用，同时参与强力链断裂后的重构。随着底部边界的上升，破碎区域面积逐渐减小，三级颗粒也逐步发生破碎形成大量二级颗粒集合体及部分二级颗粒，此时破碎区域内模型形状的统一性相对提高，导致颗粒群模型由于挤压所产生的强力链数目增多，如图11（c）和图11（d）所示。随着压缩的继续，三级颗粒及二级颗粒集合体进一步发生破碎，使得破碎区域中的二级颗粒逐渐增多，二级颗粒结构的单一性使得颗粒群模型结构更加均匀，从而使得压缩形成的力链也更加均匀的分布于颗粒群体系中，如图11（e）和图11（f）所示。同样，最终二级颗粒由于挤压的继续逐渐破碎成一级颗粒，一级颗粒为统一大小的圆形颗粒，此时颗粒群体系中颗粒之间形成的力链几乎布满整个破碎区域，并且力链的强度极大的统一，如图11（g）和图11（h）所示。

以上从力链的角度阐述了多尺度内聚颗粒模型颗粒群的振动挤压破碎过程，结果表明：通过观察力链的分布变化情况，可体现多尺度内聚颗粒模型的破碎特点，即典型形状的多尺度内聚模型三级颗粒首先受自身及相接触颗粒形状结构的影响，破碎成二级颗粒及二级颗粒集合体；随后少数存在于压缩路径上的二级颗粒会先一步破碎成一级颗粒，而二级颗粒集合体会继续破碎成二级颗粒，此过程结束后颗粒群模型结构统一性增加，结构的不均匀性减小，最终二级颗粒全部破碎成一级颗粒，完成三级颗粒颗粒群的振动挤压破碎。

4 结论

对颗粒群模型在振动及无振动条件下的挤压破碎进行分析得出如下结论：

（1）振动参数为A=2 mm、f=5 Hz下模型破碎率在任意一处压缩位移下均高于无振动情况；

（2）随着振幅的增加，在不同频率下模型破碎率大体上呈增加趋势；对比无振动条件下模型破碎率，表明振动参数有利于颗粒群模型的破碎。

（3）通过从力链的角度对颗粒群模型的振动挤压破碎过程进行分析，结果表明颗粒群模型的破碎过程依然符合多尺度内聚颗粒模型的破碎特点。

[1] HUANG J Y，XU S L，ZHENG W，et al.Compression responses of brittle granular materials subjected to dynamic loading[C]// Proceedings of 3rd International Conference on Heterogeneous Materials Mechanics.Shanghai:[s.n.]，2011：869-872.

[2] PLESHA M E，EDIL T B，BOSSCHER P J.Modeling particle damage in discrete element simulations[J].Computer Methods and Advances in Geomechanics，2001：581-585.

[3] MCDOWELL G R，BOLTON M D，ROBERTSON D.The fractal crushing of granular materials[J].Mechanics and Physies of Solids，1996，44（12）：2079-2102.

[4] 楚锡华，李锡夔.离散颗粒多尺度分级模型与破碎模拟[J].大连理工大学，2006（3）：319-326. CHU Xihua，LI Xikui.Hierarchical multi-scale discrete particle model and crushing simulation[J].Journal of Dalian University of Technology，2006（3）：319-326.

[5] 黄俊宇，徐松林，王道荣，等.脆性颗粒材料的动态多尺度模型研究[J].岩土力学，2013，34（4）：922-932. HUANG Junyu，XU Songlin，WANG Daorong，et al.Investgiations on the intrinsic mechanisms of strain rate effects of brittle granular materials[J].Chinese Jouranl of Solid Mechanics，2013，34（4）：922-932.

[6] HUANG Junyu，XU Songlin，HU Shisheng.Influence of particle breakage on the dynamic compression responses of brittle granular materials[J].Mechanics of Materials，2014（68）：15-28.

[7] DUGDALE D S.Yielding of steel containing slits[J].Journal of the Mechanics Solids，1960（8）：100-108.

[8] 王承强，郑长良.裂纹扩展过程中线性内聚力模型计算的半解析有限元法[J].计算力学学报，2006，23（2）：156-151. WANG Chengqiang，ZHENG Changliang.Semi-analytical finite elementmethod forlinearcohesiveforcemodelin crack propagation [J].Chinese Journal of Computational Mechanics，2006，23（2）：156-151.

[9] 张 东，黄晓明，赵永利.基于内聚力模型的沥青混合料劈裂试验模拟[J].东南大学学报（自然科学版），2010，40（6）：1276-1281. ZHANG Dong，HUANG Xiaoming，ZHAO Yongli.Simulation of indirect tension test of asphalt mixtures based on cohesive zone model[J].Jouranl of Southest University（Natural Science Edition），2010，40（6）：1276-1281.

[10]孙家啟，纪冬梅，唐家志.内聚力模型在裂纹萌生及扩展中的应用[J].上海电力学院学报，2016，32（2）：129-139. SUN Jiaqi，JI Dongmei，TANG Jiazhi.Application of cohesive zone model on crack initiation and propagation[J].Journal of Shanghai University of Electric Power，2016，32（2）：129-139.

[11]刘海涛，严明星.基于改进的内聚力模型模拟沥青混合料裂纹扩展[J].城市道桥与防洪，2015，8（8）：222-226. LIU Haitao，YAN Mingxing.Simulation of asphalt mixture crack propagation based on modified cohesive zone mode[J].Urban Roads Bridges&Flood Control，2015，8（8）：222-226.

Numerical Simulation for the Multi-scale Cohesive Model Particle Swarm's Vibration Extrusion

GUO Jinshan,QI Buchun,CAI Gaipin,XIA Liuyang,ZENG Yanxiang

(School of Mechanical&Electrical Engineering,Jiangxi University of Science&Technology,Ganzhou 341000,Jiangxi,China)

To determine the characteristics of irregular broken tungsten ore particles,the different shapes ore particle swarm models are built from the two aspects of the different geometry structure and multi scale cohesive.Numerical simulations of particle swarm are established under the conditions of vibration and without vibration by using EDEM. The crushing effects of these two kinds of conditions are compared by analyzing the fracture characteristics and mechanical distribution characteristics of particle swarm.The results show that:The crushing rate of particles with certain vibration parameters is higher than that without vibration.With the increase of the amplitude,the breaking rate of model at different frequencies also rises.In comparison with the model breaking rate without vibration,the vibration parameters are favorable to the fragmentation of the particle swarm model.

multi scale;cohesive force;particle swarm;vibration extrusion;crushing rate

TF351.1+1；TD453

A

10.3969/j.issn.1009－0622.2016.06.014

2016-09-14

国家自然基金项目（51464017）；江西省高等学校科技落地计划项目（KJLD13045）；江西省研究生创新专项基金项目（YC2015-S284）

郭进山（1989-），男，河南濮阳人，硕士研究生，主要研究方向物料高效破碎进技术研究。

蔡改贫（1964-），男，江西赣州人，教授，主要从事（近）净成形新技术研究与装备开发、物料高效破碎先进技术研究与装备开发。