APT无动力布料器的设计与仿真分析

刘飞飞，曾燕兵，高堂盼，古帅奇，刘龙细

（1.江西理工大学 电气工程与自动化学院，江西 赣州 341000；2.江西理工大学 机电工程学院，江西 赣州 341000）

APT无动力布料器的设计与仿真分析

刘飞飞1，曾燕兵2，高堂盼2，古帅奇2，刘龙细2

（1.江西理工大学 电气工程与自动化学院，江西 赣州 341000；2.江西理工大学 机电工程学院，江西 赣州 341000）

介绍了目前我国APT人工布料过程的基本现状，针对人工布料劳动强度大、效率低，且影响工作人员健康等问题，通过对APT无动力布料器数学模型的运动分析，研究设计了一种能够实现无动力自动均匀布料的装置。运用FLUENT软件仿真，采用k-ε湍流模型与壁面滑移相结合的方法，得到无动力布料器出口速度和出口压力云图。结果表明，进料口速度在10 m/s左右，可以驱动布料器旋转，物流均匀散落，可以实现无动力均匀布料，同时仿真结果验证了布料器设计的合理性。

APT布料器；数学模型；无动力；均匀布料；FLUENT仿真

0 引言

仲钨酸铵（简称“APT”），是钨的初级制品，是制造钨制品、硬质合金的重要原料，是中国重要的出口商品之一。在生产工艺中，制取的APT混有氯离子，此时须对APT和氯离子混合水溶液进行布料、洗涤和干燥等处理流程，以滤除氯离子，而实现布料器的均匀布料是完成APT洗涤过滤的关键环节。目前，国内外对布料机和布料器布料装置的研究，重点在两个范围：高炉炼铁和烧结矿石。此外，在冷凝造粒、垃圾焚烧、混凝土输送、道路建设等也有相关的研究，但在谷物、颗粒饲料、APT等的布料机研究上，并不多见[1]。据调查发现，目前国内绝大部分生产企业APT的布料过程都是通过管子洒在过滤池内，凹凸的地方使用人工刮平的方式，如图1所示。人工布料过程劳动强度大、效率低，不能实现均匀布料，各层的密实度不同，使得洗涤过滤不充分，不利于杂质的滤除，而且现场的氨挥发后的气味对人具有强烈的刺激性，影响操作员的情绪和健康，同时增加生产成本，甚至有时会造成生产中断，不仅浪费了钨矿等物质资源和人力资源，还影响了企业的效益。为了实现自动均匀布料，提高企业的生产效益，实现环保和节能。文章研究设计了一种节能装置，该装置依靠APT固液混合料无动力冲击驱动布料器旋转，以实现布料器自动均匀布料。

图1 APT人工布料过程Fig.1 APT artificial distribution process

1 APT无动力布料器数学模型

1.1 物料流初速度的模型

实际生产表明，物料在装料罐内的下降为“漏斗流”；而一般都采用存仓公式计算物料出装料罐的初速度v0[2]。存仓公式主要是用来求“活塞流”式的放料[3]，此公式存在使物料流量系数取值不准确的问题。

本研究数学模型中物料的初速度的计算采用水力学的连续性方程[4]。

式中：Q为实测物料出装料罐的流量，m3/s；A为装料罐的投影面积，m2；Lx装料罐的周边边长，m；Di为物料的平均粒径，m。

其中A、Lx与γ的关系如下[5]：

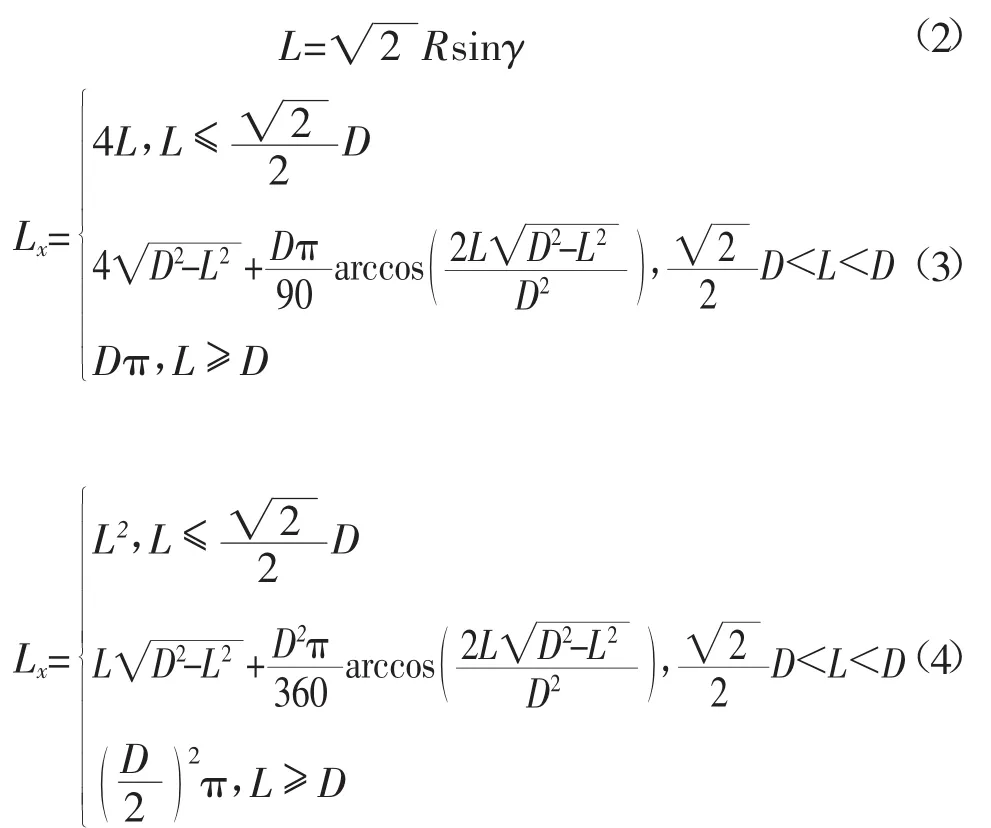
式（2）、（3）和（4）中R为装料罐内阀板旋转半径，m；D为装料罐喉管直径，m。

式（1）的Q与开度γ的关系，通过实测数据得到如下回归方程关系：

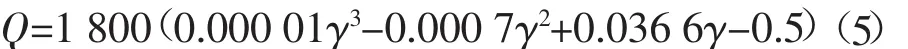
把式（2）、（3）、（4）、（5）代入（1）就可以求出不同开度物料出装料罐的初速度v0。

1.2 物料在下料管上的运动模型

物料以初速度v0落入进料口，通过APT固液混合物的冲击力驱动布料器以ω速度旋转，同时物料在竖直方向上做以加速度为g的下滑运动，假设物料的质量为m，下料管的有效长度为h。物料在下料管上的受力情况如图2所示，受到以下力：重力（mg）；旋转引起的惯性离心力（F1=-4mhπ2ω2）；管壁对物料的支持力（R=4mhπ2ω2）；管壁的摩擦力（μR）；科氏力（F2=2mvω）。物料的冲击力使布料器保持匀速转动，在相比之下，科氏力可以忽略不计。在竖直方向，物料所受力的总和如式（6）。

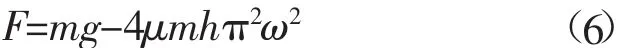
图2 物料在下料管上的受力分析Fig.2 Stress analysis of the material on the feeding pipe

1.3 物料撞击底部的速度变化

物料撞击底部，速度发生变化，同时运动方向也发生变化，伴随着对物料的冲击现象。由于物料是沿着下料管下落的，碰撞底部时物料速度发生变化。质量为m的物料以v1速度向底部冲击，在冲击瞬间发生能量损失。对于物料流中的每一个质点，碰撞是多次的，方向也各不相同，但都会因摩擦冲量而减少其运动速度。但具体减少到多大，目前还没有非常精确的计算公式，一般都是通过试验测得特定条件下的速度折算系数η，得到速度v2=ηv1。

1.4 物料流布料轨迹确定

物料的运动轨迹如图3所示，物料离开下料管末端后，在竖直方向只受到重力的作用。根据牛顿定律可以列出运动方程，如式（7）所示。

在对式（8）进行积分，积分限为：t=0，z=zl。zl为物料的自由落体有效高度。

假设布料桨叶的长度为L，则物料在离开布料桨叶到罐体底部的运动时间为t，可以用式（10）表示。

物料在布料桨叶方向上的运动距离如式（11）所示。

物料在切线方向上的运动距离如式（12）所示。

从式（11）、（12）可以求出物料落点离旋转轴中心线距离r。

同时满足r≤R，R为罐体半径，m。

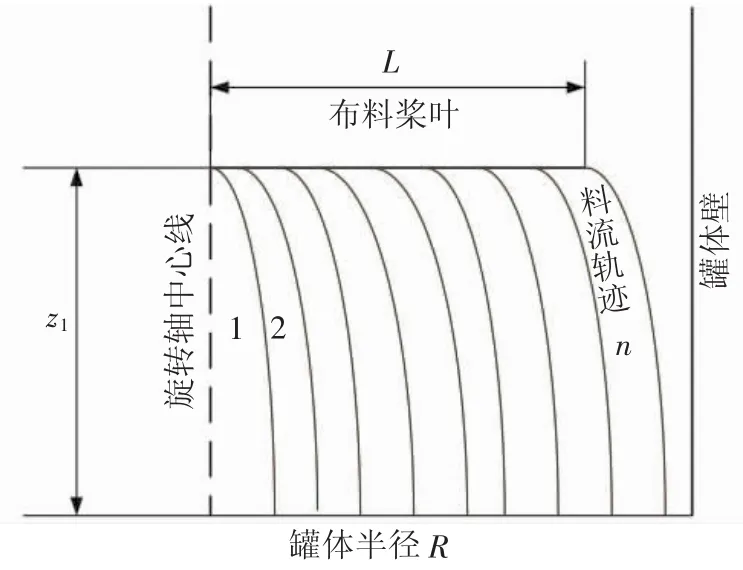
图3 物料运动轨迹示意Fig.3 Sketch map of material flow trajectory

2 APT无动力布料器的机构设计

2.1 设计流程

结合上述的数学模型分析和精度要求进行装配工艺分析，确定实现各功能的机构原理，依据机构原理进行机构和零部件的设计，完成整体结构的装配，从而使各功能在无干涉情况下实现布料动作。具体设计流程如图4所示。

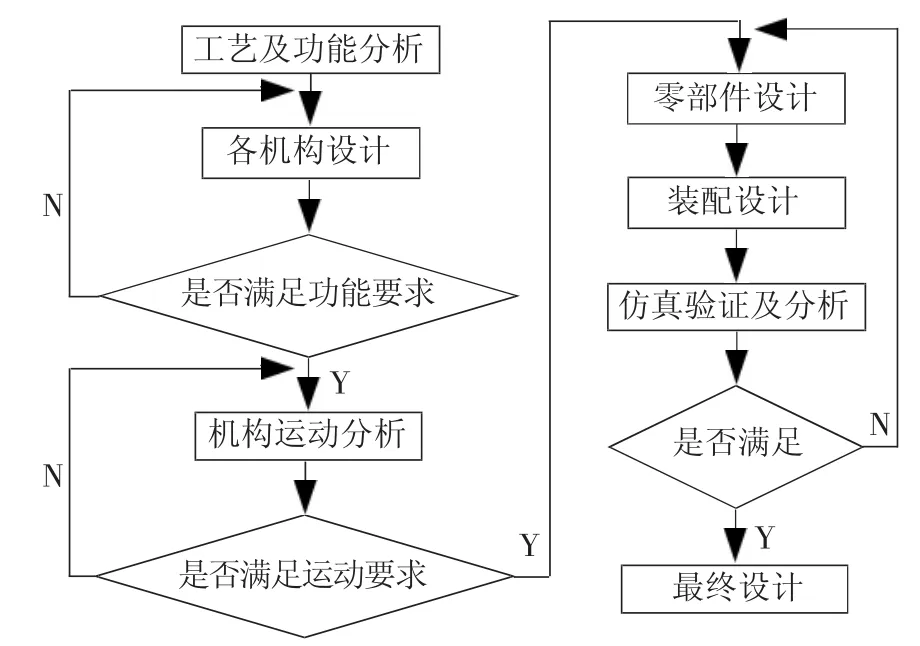
图4 设计流程Fig.4 Flow chart

2.2 总体设计

总体设计如图5，包括进料口，洗涤入口，在洗涤入口和进料口交汇处下方设置上罐体，上罐体上设置有布料组件，上罐体旁边设置有气缸，气缸设置在固定的横梁上。物料在一定的高度以一定的速度从进料口进入，靠着物料的冲击力驱动涡轮式布料器，使布料器旋转起来，实现均匀布料，物料流轨迹不重叠，各层密实度一致。

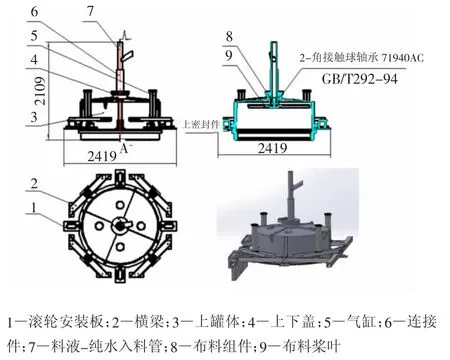
图5 APT无动力布料器总体设计Fig.5 General design of APT without power distributor

2.3 布料机构设计

物料通过进料口连续的加入冲击布料组件导料桨叶，使布料组件旋转，接着物料沿着导料桨叶流向布料桨叶，物料随着布料组件的旋转，沿布料桨叶均匀的散落在上罐体、下罐体和过滤介质组成的腔体内，同时抽滤口打开，将物料中的液体抽离，进行干燥操作。布料组件三维模型如图6所示。

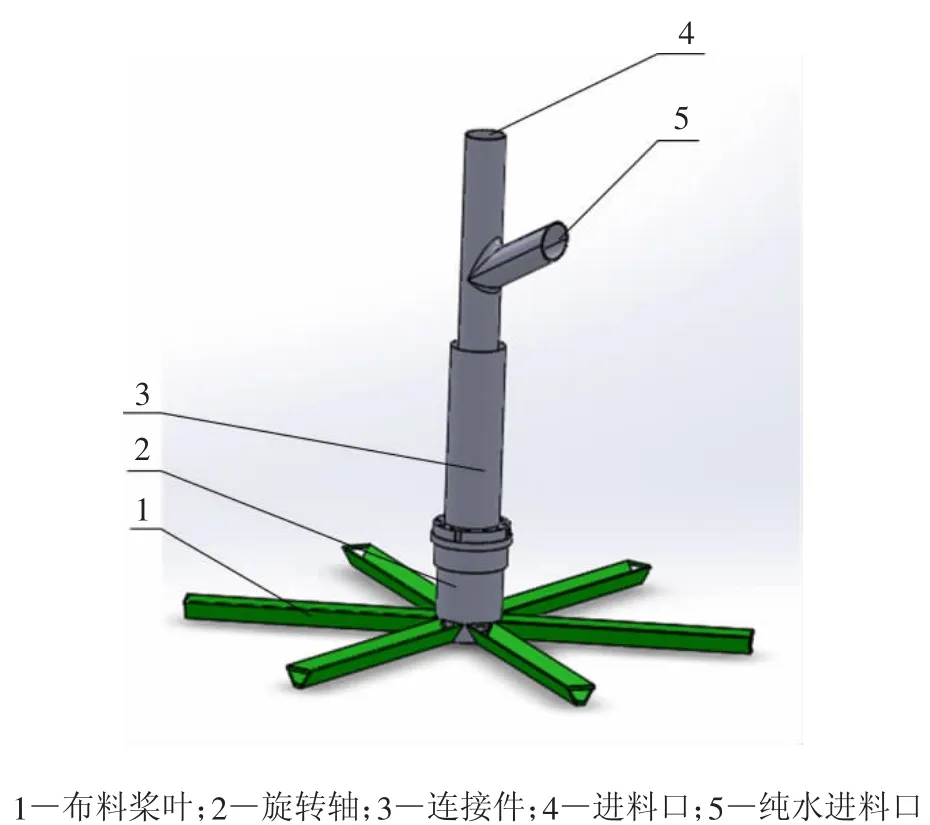
图6 布料组件三维模型Fig.6 3D model of distributing assembly

布料组件主要机构如图7所示。包括旋转主轴、套筒、传动部分、涡轮导料桨叶和布料桨叶。

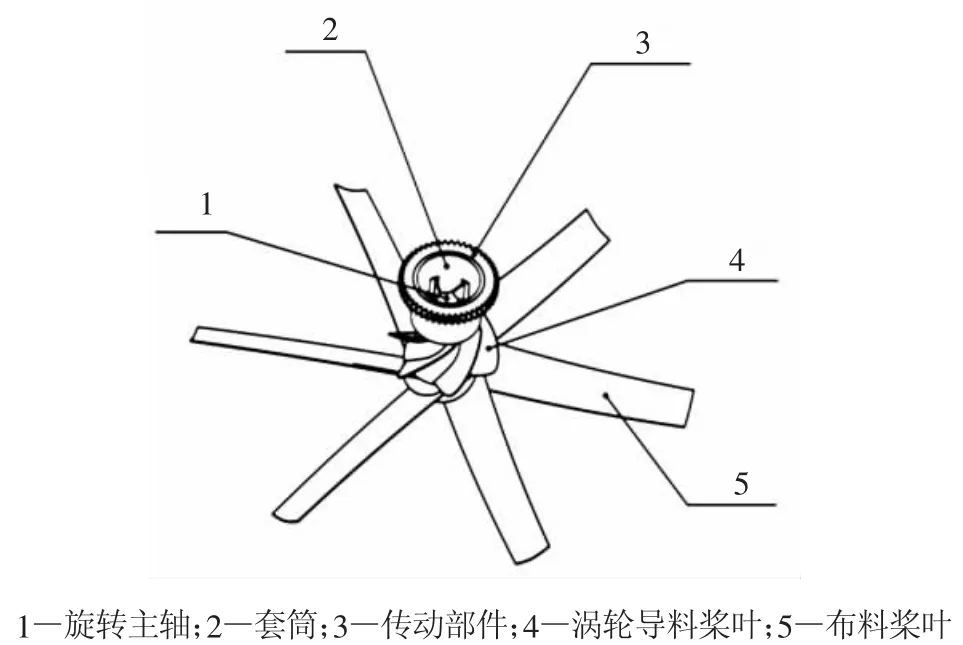
图7 布料组件主要机构Fig.7 Major mechanism for distributor

3 APT无动力布料器FLUENT仿真

从上述的分析可知，整个布料过程，并不是规则统一的，流体的流动杂乱无章，仅仅采用数值分析的方法显然很难得出流体的流动情形，为了进一步分析流体的流动，在设计过程中采用了FLUENT流体仿真方法对布料组件进行了分析。

3.1 湍流模型

FLUENT提供的湍流模型包括：k-ε模型，SST模型，SSG模型和BSL模型，它们各有优、缺点。其中k-ε湍流模型是应用最广泛、最完整的湍流模型，计算速度快，能较精确的预测物料流的散布率。其中湍流方程为：

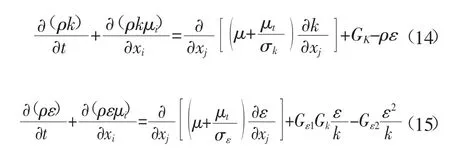
该模型假设流动为完全湍流，分子黏性的影响可以忽略。它能较好地解决较小压力下的自由剪切流问题，但当逆压梯度变大时并不适用，并且两方程模型计算量大，收敛困难，对网格划分要求严格。

3.2 网格划分

为了提高网格的质量，初始计算网格由FLUENT软件中的Gambit程序完成。为了便于仿真，简化模型。将Solidworks建立的布料组件三维模型导入前处理软件Gambit中，进行结构化网格划分。网格划分结果如图8所示，生成的网格为六面体结构化网格，网格总数为85 982个。

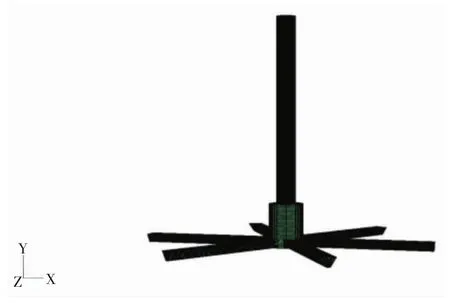
图8 Gambit网格划分结果Fig.8 Division results of Gambit grid

3.3 边界条件的设定与计算方法

在FLUENT仿真计算中，设置边界条件是仿真结果正确与否的一个关键因素。文中研究的流体是APT，其液态密度是2.2g/cm3，动力黏度是0.32MPa·s；流体的初始速度设置为10 m/s，方向垂直于截面，进料口直径为100 mm，长度1 500 mm。采用k-ε湍流模型与壁面滑移函数处理法相结合的方法，有效地提高了计算结果的精确度，并且对二次流现象的模拟效果更加显著。设置迭代次数为600次，计算并输出结果。

3.4 仿真与结果分析

使用FLUENT软件求解流场，计算结束并观察残差曲线（图9）是判断收敛的最基本方法。大多数情况下残差下降4个数量级（即收敛精度为10-4），就可以认为计算已经收敛。从图9中可知，上述设置的参数符合要求，使仿真得到收敛。通过简化仿真模型，可以大大地减少仿真时间，提高仿真速度，使仿真的结果更加准确。从速度分布图（图10）、出口速度分布图（图11）和出口压力分布图（图12）可以看出，进料口速度在10 m/s左右，物料的冲击力可以驱动涡轮式布料器旋转起来，离旋转轴越远，速度越大，物料均匀散落，物料流轨迹不重叠，各层密实度一致，可以实现无动力均匀布料，同时出口的压力也保持稳定，这与实现均匀布料的要求一致，说明模拟结果是合理的，机构的设计是正确的。

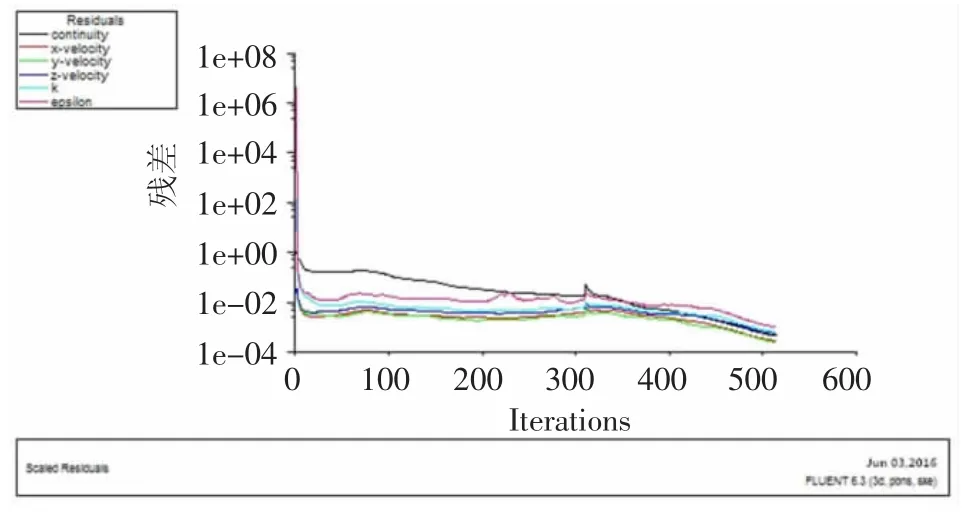
图9 残差曲线Fig.9 Residual curve

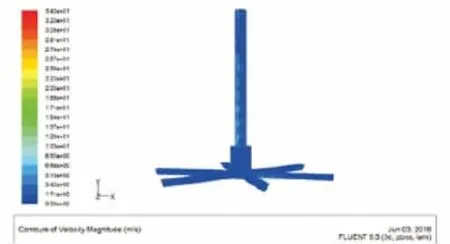
图10 速度分布图Fig.10 Velocity distribution diagram

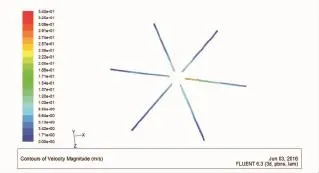
图11 出口速度分布图Fig.11 Velocity distribution diagram for outlet

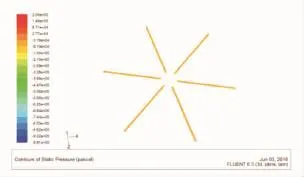
图12 出口压力分布图Fig.12 Distribution diagram for outlet pressure

4 结论

（1）采用k-ε湍流模型与壁面滑移函数处理法相结合的方法，对布料器内部的流体进行仿真，能够较好的模拟内部的二次流现象。对以后布料器内部的仿真提供一定的理论基础，同时有很好的借鉴意义。

（2）在布料器内部流体的初始速度设置为10m/s，进料口直径为100 mm，长度1 500 mm情况下，能够满足要求。初始速度偏小，布料器不能够旋转，实现不了均匀布料；初始速度偏大，布料器能够旋转，但是实现不了均匀布料。同时改变初始速度和进料管的长度也可以得到布料器旋转，实现均匀布料的这一结果。

[1] 王维兴.中国炼铁技术发展评述[J].河南冶金，2008，16（5）：4-9. WANG Weixing.Comments on the development of China's iron making technology[J].Henan Metallurgy，2008，16（5）：4-9.

[2] 刘云彩.高炉布料规律[M].北京：冶金工业出版社，2005.

[3] 陈令坤，于仲洁，周曼丽.高炉布料数学模型的开发及应用[J].钢铁，2006，41（11）：13-16. CHEN Lingkun，YU Zhongjie，ZHOU Manli.Blastfurnace mathematical model of the development and application of[J]. Steel，2006，41（11）：13-16.

[4] 王 平.串罐无料钟料流轨迹与宽度测定及其分析 [J].钢铁，2003，38（3）：8-12. WANG Ping.Measurement and analysis of the track and width of the bell less material flow in a series of bell jar[J].Steel，2003，38（3）：8-12.

[5] 闫洪波，郑 鸿，张玉宝，等.基于Solid Edge的包钢BG-Ⅲ型布料器设计[J].机械工程师，2010（9）：89-91. YAN Hongbo，ZHENG Hong，ZHANG Yubao，et al.The design of solid type III distributor of steel clad steel BG-mechanical engineer based on Edge[J].Mechanical Engineer，2010（9）：89-91.

[6] 朱红钧，林元华，谢龙汉.FLUENT 12流体分析及工程仿真[M].北京：清华大学出版社，2011：1-5.

[7] JOAN C.Developments in the north American iron and steel industry[J].Iron＆Steel Technology，2004，1（3）：23.

[8] 邱立杰，张国福，郝 明.基于FLUENT的弯管内部流场的数值模拟[J].辽宁石油化工大学学报，2013，33（1）：48-52. QIU Lijie，ZHANG Guofu，Hao Ming.Numerical simulation of internal flow field of elbow pipe based on FLUENT[J].Journal of Liaoning Shihua University，2013，33（1）：48-52.

[9] 朱清天，程树森.高炉料流轨迹的数学模型[J].北京科技大学学报，2007，29（9）：932-936. ZHU Qingtian，CHENG Shushen.Mathematical model of blast furnace material flow path[J].Journal of University of Science and Technology Beijing，2007，29（9）：932-936.

[10] YAO Meihong，ZHANG Hengfeng.Numerical study of aerostatic bearing based on CFX[J].China Mechanical Engineering，2012，23（22）：2681-2684.

Design and Simulation Analysis of APT without Power Distributor

LIU Feifei1,ZENG Yanbing2,GAO Tangpan2,GU Shuaiqi2,LIU Longxi2

(1.School of Electrical Engineering and Automation,Jiangxi University of Science and Technology,Ganzhou 341000,Jiangxi,China;2.School of Mechanical and Electrical Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,Jiangxi,China)

Based on introducing the current situation of APT artificial material distribution process,we designed a device through the motion analysis of distributor mathematical model.The invention can realize the automatic uniform distribution without power by overcoming the disadvantages of the artificial process,including labor intensity,low efficiency,and harmful to workers'health.The outlet velocity and outlet pressure diagram are obtained by FLUENT software based on the turbulence model and wall slip.The results show that the distributing device can be driven to rotate when the inlet velocity is about 10 m/s,and the logistics evenly scattered.Therefore,the uniform distribution can be realized.At the same time,the simulation results verify the rationality of the design of the distributor.

APT distributor;mathematical model;no power;uniform distribution；FLUENT simulation

TF302；TF351.2

A

10.3969/j.issn.1009－0622.2016.06.013

2016-06-20

刘飞飞（1962-），男，江西信丰人，教授，博士，主要从事矿冶装备及其自动化、检测技术和特种装备机器人方面的研究。