向量背景下的面积问题



向量背景下的面积问题

林波

(江苏省扬州大学数学科学学院,225002)

随着新课标的实施,向量进入了中学数学,从而改变了中学几何教学的内容与形式,同时也影响和改变着中学生的思维模式与方式.近年来,出现了以向量为背景的面积问题,给我们提出了新的课题.本文首先给出向量坐标下的三角形面积公式,再举例说明它的应用,以期抛砖引玉.

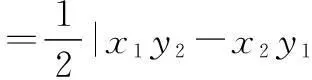
分析参考答案是利用线性规划思路作出平面区域D,若从向量加法的平行四边形法则与数乘向量的定义考虑,则过程更为简洁.

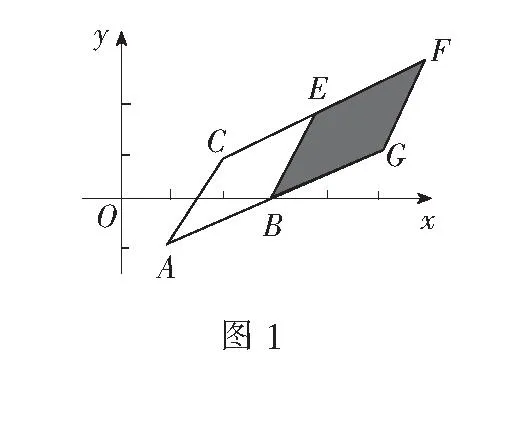
分析解决本题的关键是弄清λ、μ的几何意义.

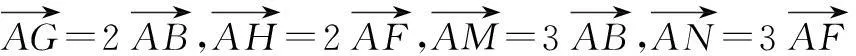
λ+μ=3t+3(1-t)=3.

同理可知,当点P在直线GH上时,

λ+μ=2.

因此,所求点P组成区域为图中阴影矩形,其面积

(1)求双曲线的离心率;

(2)设O为坐标原点,动直线l分别交直线l1,l2于A,B两点(A,B分别在第一、四象限),且∆OAB的面积为8.试探究:是否存在总与l有且只有一个公共点的双曲线E?若存在,求双曲线E的方程;若不存在,说明理由.

联立l与l1的方程,解得

例5已知过定点P(2,0)的直线l交抛物线y2=4x于A、B两点,若O为坐标原点,求∆OAB面积的最小值.

①

整理得y1y2=-8.

②