三角函数“变角”技巧的探究



三角函数“变角”技巧的探究

郭俊

(江苏省南京市东山外国语学校，211103)

从2007年至2015年的高考题来看:历年来三角函数是高考的重头戏,而在三角函数的求值、化简和证明的过程中,往往又会出现很多相异的角,这时我们必须要理清角与角之间的关系,要懂得观察它们之间的角的特征.如果我们在解题过程中缺乏对角的分析,加上三角函数的公式众多,就会导致考生对三角函数“难以把握”,因此我们有必要掌握“变角”的技巧,真正地识别“变角”的“玄机”.下面就三角中常用到的一些变角技巧来进行举例分析,让我们一起来领悟“变角”的实质,真正地掌握“变角”的技巧,使考生在运用“变角”时达到融会贯通的境界.

一、 “变角”的实质

在解决三角函数问题时首先要熟练三角公式,要对公式的“正用、逆用、活用”熟练掌握,同时要对“变角”的本质进行把握,所谓的“变角”法,实际上就是一种整体运算思想在以三角问题中的形式的再现,用已知角来表示所求角.因此只要我们在解题过程中把握其“实质”——找出“已知角”和“目标角”的关系,用“已知角”来表示目标角,通过对角进行“拆、凑、配”等操作,最终很好地将问题解决.

解由α,β为锐角,知0<α+β<π,

所以sin(α+β)>0,cosβ>0,所以

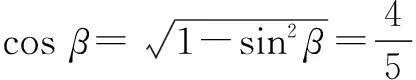
所以sinα=sin[(α+β)-β]

=sin(α+β)cosβ-cos(α+β)sinβ

评注从上面的过程分析可知:对于三角函数的“变角”策略首先是要观察已知角与目标角之间的关系,要通过对角恰当的凑、拆、配等基本操作技巧来找出已知角与目标角之间的关系,α=(α+β)-β是例1求解的关键.从上面的解答过程我们可知:利用‘配角法’求值时一般分为三步:一是找出已知角和目标角之间的关系,二是求相关已知角的范围,三是求出相关角的三角函数值,特别是第一步直接关系到第二步计算正确与否.

分析本题只要观察已知角α+β、α-β和目标角2α之间的关系,懂得将2α=(α+β)+(α-β)表示出来,问题就可以解决了.

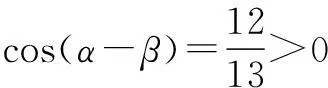
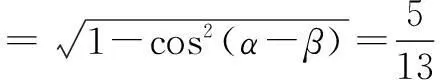
所以sin 2α=sin[(α+β)+(α-β)]=sin(α+β)cos(α-β)+cos(α+β)sin(α-β)

二、 “变角”的活用

在解题过程中弄清楚已知角与未知角之间的内在关系,要懂得选取一个目标,其余各个角都朝着这个目标转化,再按照题意配出相应的角,最终创造出使用三角函数的有关公式的条件,以达到化简和论证的目的.

cos(α+45°)

∴sinα=sin[(α+45°)-45°]

=sin(α+45°)cos 45°

-cos(α+45°)sin 45°

评注本题若将sin(α+45°)展开为sinα、cosα的表达式，再结合sin2α+cos2α=1解方程组求sinα,则过程繁琐. 但借助非特殊角α与特殊角45°的关系,用α=(45°+α)-45°进行配凑，显然简化了求解过程.

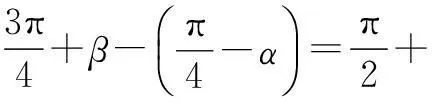
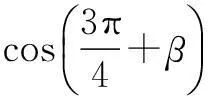
只要应用两次诱导公式就可以解题.

所以cos 2x

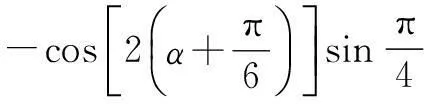
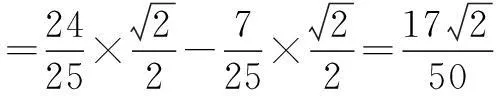
从上面的例题分析可以知:我们要在解题中充分理解变角的实质,当已知条件中的角与所求角不同时,需要通过恰当的“拆”、“凑”、“配”等方法实现角的转化,一般是寻求它们的和、差、倍、半等关系.在实行变角的过程中,有时需用特殊角帮助实现角的转换，有时还要整体地进行考虑,懂得用整体代换的思想来解决问题.