思维品质在初中数学教学中的培养

李楷春

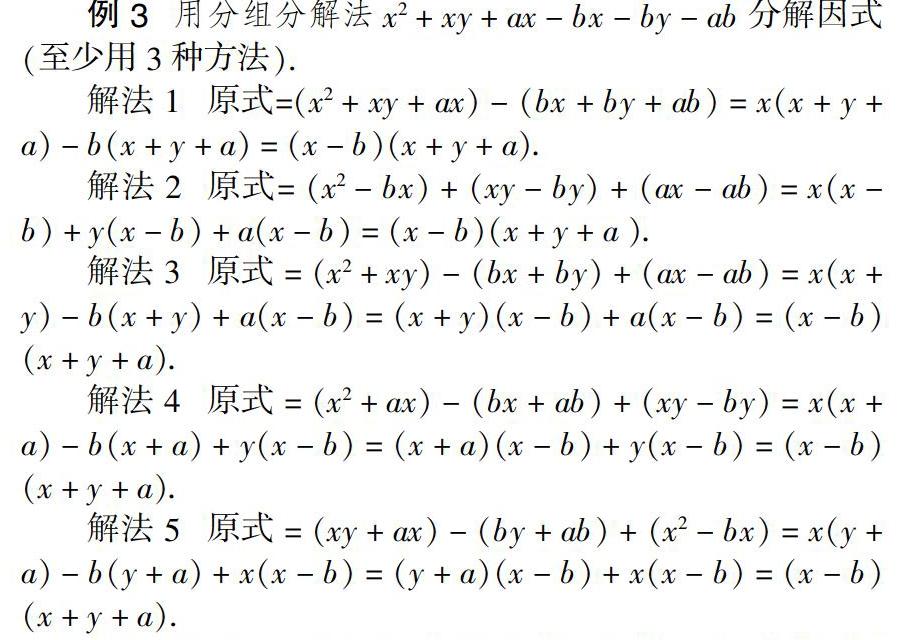
【摘要】 灵活性、批判性、严谨性和广阔性是数学的基本思维品质，本文探讨了在初中数学课堂教学过程中培养学生思维品质的策略与方法.

【关键词】 数学教学；思维品质；数学思维

数学是思维的体操，数学教学的目的不仅使学生掌握知识，更重要的在于培养学生的思维能力，而要做到这一点，必须培养学生良好的思维品质.

一、善于观察，联想转化，培养学生思维的灵活性

观察是认识事物最基本的途经，它是了解问题、发现问题和解决问题的前提，是联想的基础. 联想是问题转化的桥梁，转化是解数学题的一种十分重要的方法. 怎样解题及解题的速度如何取决于能否由观察到的特征，灵活运用有关知识，作出相应的联想，找到问题的突破口，不断深入，把复杂问题转化为简单问题，把抽象问题转化为具体问题.

例1 已知m < 0，n > 0且m + n < 0.试比较m，n，-m，-n，m - n，n - m的大小.

分析 这是比较有理数大小的问题，直接比较抽象复杂. 因为在数轴上表示的数，右边的总比左边的大，由此联想到数形结合的数学思想，通过数轴来比较这几个数的大小. 根据已知条件m < 0，n > 0且m + n < 0.得|m| > |n|， 把m，n，-m，-n，m - n，n - m这6个数转化在数轴上：

这样很容易比较出它们的大小m - n < m < - n < n < - m < n - m ，充分体现了思维的灵活性.

二、善于提出问题，敢于发表自己的见解，培养学生思维的批判性

学生在解题的过程中，往往受思维定式或别人提示的影响，解题盲目附和，不能提出自己的看法，这不利于培养思维的批判性，只有鼓励学生积极地独立思考，对题目解法发表自己的见解，才能增强思维的批判性.

例2 一次考试出了25道题，答对一题给4分，不答或答错一题倒扣1分，如果一名学生得90分，他答对了多少道题？

解 设他答错了x道题，根据题意，得25 × 4 - 5x = 90.解得x = 2，∴ 25 - x = 25 - 2 = 23.所以他答对了23道题.

分析 传统的思维方法是：设他答对了x道题，则答错了（25 - x）道题，根据题意，得4x - （25 - x） × 1 = 90，解得x = 23，他答对了23.道题. 上面这名学生的解法没有盲目附和，他考虑到试卷满分25 × 4 = 100分，错一道题实际要扣5分，那么错x道题实际要扣5x分，根据题意列出方程25 × 4 - 5x = 90，先算出答错了2道题，在算出答对了23道题. 在这里学生能对题目敢于发表自己的独特见解，有助于思维批判性的培养.

三、准确把握概念和判断，全面思考问题，培养学生思维的严谨性

概念含糊不清是思维不严谨的体现，也是解题出错的主要原因，因此在教学中，讲解概念要始终抓住事物的本质，事物的全体、事物的内部联系，把概念的内涵和外延讲明白，对容易出错的地方，可以有意制造若干错误结论，让学生发现，以加深对概念的理解.

例如，在讲“点到直线的距离”这一概念时，有意提出以下几个错误结论：（1）从直线外一点到这条直线的垂线的长度叫做点到直线的距离；（2）从直线外一点到这条直线的垂线段叫做点到直线的距离；（3） 从直线外一点到这条直线的线段的长度叫做点到直线的距离；让学生辨析，使他们准确把握点到直线的距离是从直线外一点到这条直线的垂线段的长度，是“数量”而不是“图形”.

数学上定理和公式都是在一定的条件下成立的，如果忽略了成立的条件，解题中难免会出现错误，因此要引导学生注意公式和定理成立的条件. 思考问题不全面，以偏概全是中学生常犯的错误，它是思维不严谨的突出表现. 要纠正学生的这种错误，必须经常指导学生全面审题，找出问题的各种可能性，使他们养成全面考虑问题的良好思维习惯. 四、一题多解，培养学生思维的广阔性

通过不同的方法解同一道数学题，可以开阔学生的思路，巩固所学知识，还可激发学生学习的积极性，提高他们学习数学的兴趣，一题多解不但要注意每种解法的特点，而且要善于发现解题规律，从中找出最有意义的简捷方法，教师引导学生进行一题多解，关键是教会学生如何思考，只有“从结论出发，紧扣题目的已知条件”的思考方法，才是解题的万能钥匙，只有学会思考，才能使问题迎刃而解.

例3 用分组分解法x2 + xy + ax - bx - by - ab分解因式（至少用3种方法）.

解法1 原式=（x2 + xy + ax） - （bx + by + ab） = x（x + y + a） - b（x + y + a） = （x - b）（x + y + a）.

解法2 原式= （x2 - bx） + （xy - by） + （ax - ab） = x（x - b） + y（x - b） + a（x - b） = （x - b）（x + y + a ）.

解法3 原式 = （x2 + xy） - （bx + by） + （ax - ab） = x（x + y） - b（x + y） + a（x - b） = （x + y）（x - b） + a（x - b） = （x - b）（x + y + a）.

解法4 原式 = （x2 + ax） - （bx + ab） + （xy - by） = x（x + a） - b（x + a） + y（x - b） = （x + a）（x - b） + y（x - b） = （x - b）（x + y + a）.

解法5 原式 = （xy + ax） - （by + ab） + （x2 - bx） = x（y + a） - b（y + a） + x（x - b） = （y + a）（x - b） + x（x - b） = （x - b）（x + y + a）.

分析 这是一道考察分组分解因式的习题，分组分解因式的关键是分组要合理，分组后分解因式能够继续进行下去，解法1、2较简单，分组后直接提公因式，解法3、4、5难度较大，它们都分成3组，但分组后3组之间没有公因式，而前两组之间有公因式，前两组之间提公因式后，才能与第三组之间产生公因式. 解法3、4、5的分解思路由解法1、2的分解结果（x - b）（x + y + a）挖掘出来较为简单，因为分解结果有因式（x+y+a），这一因式可变形为[（x + y） + a]、[（x + a） + y]、[（y + a） + x]，由此推出解法3、4、5. 经过以上分组训练，可提高学生分组分解因式的能力，拓宽解题思路，培养他们思维的广阔性.

数学思维的灵活性、批判性、严谨性和广阔性这四种思维品质不是孤立的，它们是相互联系、相互渗透、相互制约的. 只有全面发展这四种思维品质，才能有效地培养学生的思维能力，从而提高他们的数学素质.