扫描高考中的线性规划问题



扫描高考中的线性规划问题

罗礼明

(湖南省炎陵县第一中学，412500)

线性规划问题在实际生活、生产中应用十分广泛,也是高中数学中的重点内容之一.近年来在全国各地的高考数学命题中,线性规划类问题已逐步成为高考的一个新热点,它以其实用性、工具性和交互性,备受人们的关注.题型也越来越开放,从单一的、静态的线性规划发展到较全面的、动态的线性规划.常有一些综合性、探索性等新型试题出观.本文以近两年高考中的线性规划题为例,就线性规划问题进行归纳总结.

一、静态可行域下的目标函数最值问题

1.形如z=ax+by+c截距型线性目标函数的最值

(A)-7(B)-1(C)1(D)2

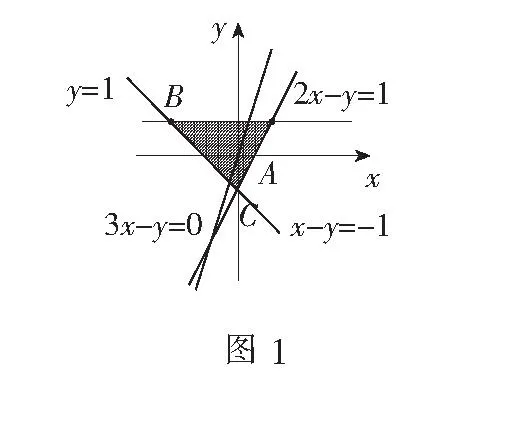
分析作出可行域,作直线l:3x-y=0,平行移动l利用数形结合法求最值.

解画出可行域如图1中的阴影部分,作直线l:3x-y=0,平移l,可知当x=-2,y=1时,zmin=3×(-2)-1=-7,故选A.

评注对线性规划问题,求目标函数的最值的一般步骤为:一画二移三求.其关键是准确作出可行域,理解目标函数的意义.利用z的几何意义,结合可行域找出取最值的点,通过解方程组求出最优解,代入目标函数,求出最值.在画可行域时,首先必须找准可行域的范围,其次要注意目标函数对应的直线斜率的大小,从而确定目标函数取到最优解时所经过的点.

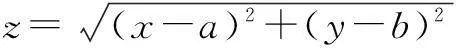
(A)[2,8] (B) [4,13]

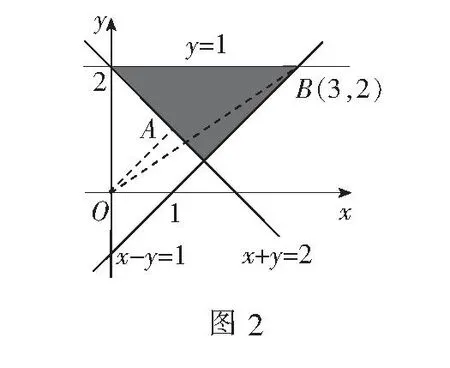
分析将目标函数z=x2+y2看作可行域中的点P(x,y)与原点距离的平方来求解.

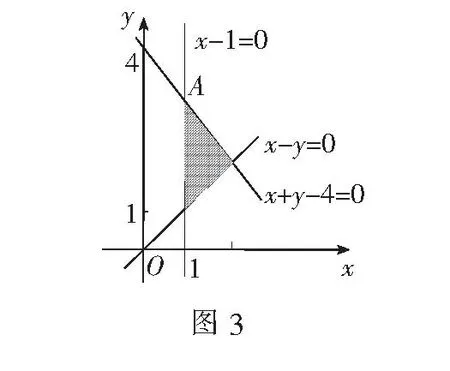
解可行域为如图2所示的三角形内部及其边界,z=x2+y2表示可行域中的动点P(x,y)到原点O(0,0)距离的平方.从而有

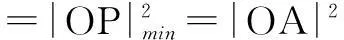
二、动态可行域下的线性目标函数问题

1.形如z=ax+by+c截距型线性目标函数逆向问题

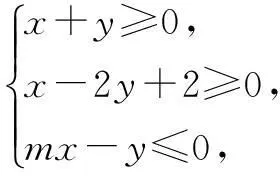
(A)-2(B)-1(C)1(D)2

评注本题考查含参数的线性规划问题,解此类问题要善于从已知的可行域(动态区域)中找出不变的区域.先要对目标函数进行分析,什么时候目标函数取到最大值,其次要对m的符号讨论,以确定可行域.解该类题目时候,往往还要将目标直线的斜率和可行域边界的斜率比较,否则很容易出错.

2.平面区域的面积问题

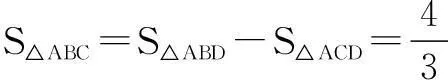
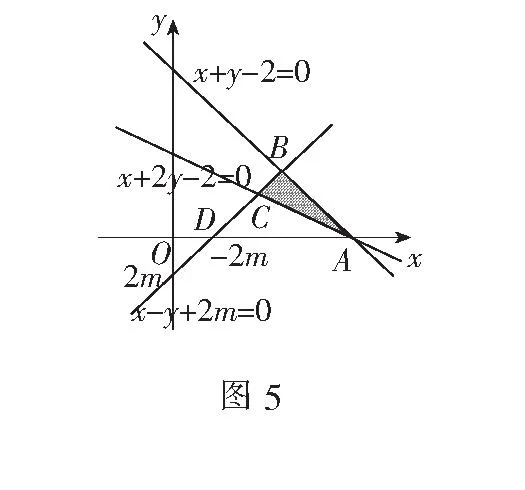
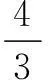
评注平面区域的面积问题主要有两类题型:(1)求已知约束条件下平面区域的面积;(2)根据平面区域面积的大小求所含参数的值.求解时需抓住两点:① 正确判断平面区域的形状,如果形状不是常见的规则平面图形或面积不易求,则需要进行分割;② 求参数问题时一般涉及一条动直线,确定其位置至关重要,有时还需要对动直线的位置进行分类讨论.

三、线性规划与其他知识的交汇

1.线性规划与柯西不等式的整合

分析先由线性目标函数的最优解得出a,b的关系式,再用柯西不等式求a2+b2的最小值,也可以转化为二次函数求最值.

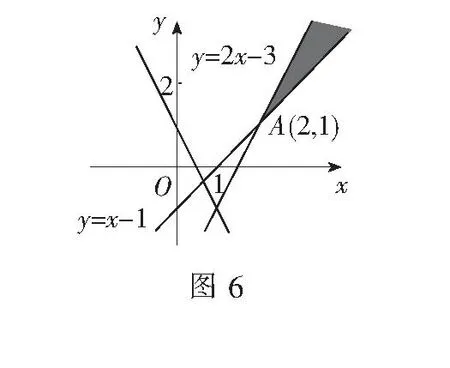
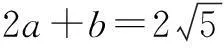
2.线性规划与平面向量的整合

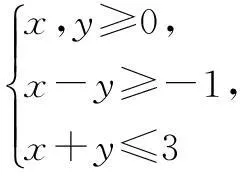
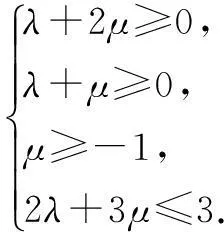
作出不等式组表示的平面区域,得到如