一种栅格化矢量地图的拾取交互方法

俞 信,郭 毓,王 洋

(1.南京理工大学 自动化系，江苏 南京 210094；2.中国科学院电子学研究所苏州研究院，江苏 苏州 215000)

一种栅格化矢量地图的拾取交互方法

俞 信1,郭 毓1,王 洋2

(1.南京理工大学 自动化系，江苏 南京 210094；2.中国科学院电子学研究所苏州研究院，江苏 苏州 215000)

针对纹理法渲染的栅格化矢量地图难以直接进行交互的问题，设计了一种栅格化矢量地图的拾取交互方法。基于实际面型矢量顶点数目多、多边形分离、空洞多边形等特性，改进了传统的射线求交判断点是否在多边形内的算法，使其可适用于实际面型矢量拾取；同时，提出了一种基于半平面连续链的新型内角和算法，可大幅降低传统内角和算法的计算量，实现了栅格化矢量地图的拾取交互。应用不同复杂程度的矢量数据进行相关实验，结果表明，在明显提高矢量渲染效率的同时，避免了在三维场景下矢量渲染不贴地的情况下，可以实现矢量兴趣要素拾取，且所提矢量拾取方法实时性良好，拾取响应时间只取决于矢量数据本身复杂度，与三维地形复杂度无关，可以满足GIS的需求。

矢量地图交互；要素拾取；栅格化；射线求交；内角和

0 引 言

空间查询和交互是地理信息系统(GIS)的必备功能，无论是二维还是三维GIS，现有的实现方法都是通过鼠标的点选方式获取矢量要素的空间坐标，执行矢量高亮显示和属性查询操作[1-2]，这种方法的前提是场景中的矢量地图是基于几何法渲染的。文献[3]从屏幕发出射线与地形节点进行相交运算获取地理坐标，计算得到地理包围矩形，继而得到该地理包围矩形内的矢量要素数据。文献[4]采用视点相关的数据动态调用策略，实现了视景体内矢量线、面对象的动态查询和检索，此方法取决于三维地形数据的复杂度。文献[5]提出了只考虑当前屏幕中可见矢量要素的方法，提高了拾取效率。

目前，三维场景下的矢量地图渲染方法主要分为两种：几何法[6-8]和纹理法[9-10]。几何法中，二维矢量与三维地形融合过程复杂，需要不断计算顶点位置，在顶点之间进行插值，效率较低，不合理的插值会出现矢量数据的“悬空”或“入地”现象，难以确保矢量数据贴合地面[11]。纹理法将矢量数据栅格化为纹理后，通过纹理映射投影到三维地形上，无需考虑矢量数据贴地的问题，且效率较高，但较之几何法，纹理法可能会导致在相机视距较小时出现边缘走样[12]。另外，针对矢量地图交互问题，几何法可以直接利用射线法与矢量模型节点作相交测试得到兴趣要素，进行后续的高亮和属性查询等操作；而纹理法无法直接进行矢量地图交互，其本质是利用栅格化后的地图加载效率而舍弃了矢量的实时可交互性。相较于几何法，纹理法的优势是其较高的渲染效率使矢量数据与三维地形完美的融合。

为此，设计了一种栅格化矢量地图的交互方法，基于实际面型矢量顶点数目多、多边形分离、“空洞”多边形等特性，对普通的射线求交判断点是否在多边形中的算法进行了改进，提出了一种基于半平面连续链的新型内角和算法，提高了拾取效率。此交互方法既保留了栅格化矢量地图渲染快、贴合地面的优点，又能进行拾取交互，解决了栅格化矢量地图难以直接进行交互的问题。利用不同复杂度的矢量数据进行交互实验后，在矢量地图渲染效率明显提高的前提下，拾取效率良好，证明所提方法可用于实际GIS系统。

1 栅格化矢量地图拾取交互设计

1.1 坐标转化

空间坐标的相互转化是矢量地图交互的基础。矢量地图拾取交互操作的第一步是鼠标点击，点击处获取的是屏幕坐标，而大多数矢量数据存储的坐标信息都是基于WGS84经纬度坐标系的。因此，需将屏幕坐标转换为常用的经纬度坐标。

首先，从屏幕坐标系转换到世界坐标系，转换表达式为：

(1)

其中，Mmodel-view、Mprojection和Mscreen分别代表参与坐标变换的模型视点矩阵、投影矩阵和窗口矩阵。

接着，从世界坐标系转换到经纬度坐标系。经度、高度和纬度的计算表达式如下：

L=tan-1(Y/X)

(2)

(3)

(4)

其中，X,Y,Z为世界坐标系的三个坐标；L,N,H为经纬高三个分量。

1.2 拾取交互流程设计

与栅格数据相比，矢量数据最大的优势是支持空间分析以及属性查询。当采用纹理法渲染矢量数据时，矢量数据转化为栅格数据，按照栅格的方式渲染至三维场景中，此时不能按照传统的几何法渲染的矢量地图的交互方式实现拾取。文中设计的栅格化矢量地图拾取交互方法流程如图1所示。

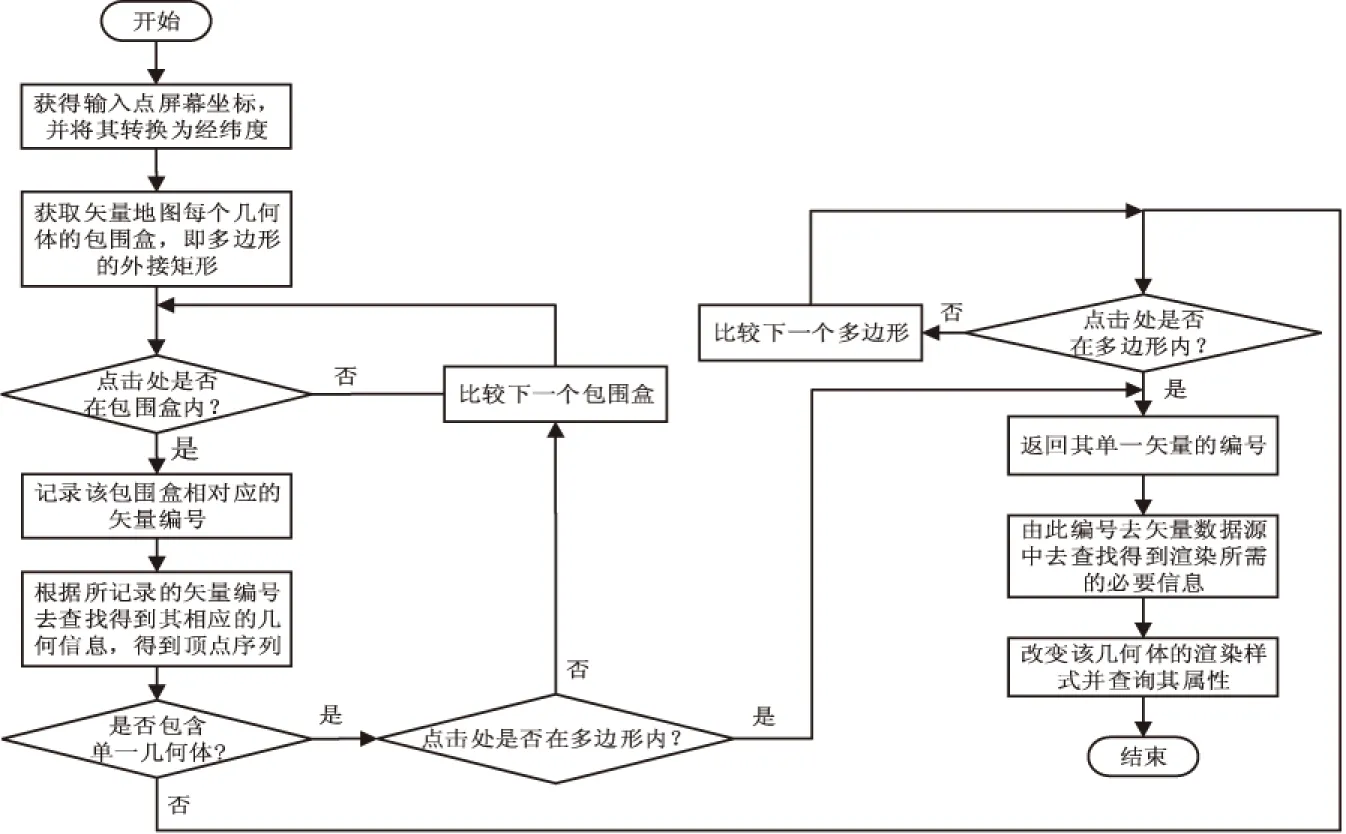
图1 栅格化矢量地图拾取流程

对图1有以下几点说明：

(1)执行包围盒与点位置的包含关系判断的原因是：当点不在矢量要素的包围盒内时，一定不在矢量要素中的多边形中，当点位于包围盒里时再执行判断算法，提高了计算效率。

(2)经包围盒的位置判断得到矢量要素，若矢量要素的几何类型为单一的多边形时，无需分离其几何体，只需执行点是否在多边形内的判断即可；若一个矢量要素包含多个几何体时，则需分解要素，继而执行改进后的点在多边形内的判断算法。

(3)由于矢量地图拾取的唯一性，只需满足点在多边形内即可获得包含输入点的几何要素编号，即可跳出循环，提高检索效率。

由图1可知，栅格化矢量地图的拾取交互问题转化成为点是否在多边形内的判断问题，拾取效率将取决于点在多边形内判断算法的执行效率。

2 问题描述

2.1 射线求交法存在的问题

传统射线求交法[13]的基本原理为：对于普通凸多边形而言，只要从所选点向左延伸一条射线，得到与多边形的交点个数，若交点个数为奇，则该点在多边形内，否则该点不在多边形内。

传统射线求交法适用于单一的多边形，由于面型矢量数据的特殊结构，它不适用于实际面型矢量。如中国海南岛，在地图上与其他省份属于分离的多边形；南非内的莱索托国，一个多边形内有一个或多个“空洞”。当在此类矢量地图上进行拾取操作时，用户需要将该矢量要素全部显示为高亮，而不是点击中国时，不显示海南岛。

2.2 内角和算法的不足

内角和的基本原理为：点Q与多边形P的每条边界构成的夹角之和若为±2π，则Q在P内，否则，Q在P外。对于单一的，顶点数目较少的多边形而言，内角和算法简单快捷，但是对于实际的矢量数据而言，多边形顶点繁多，且无规则可言。计算每一个边界内角时需进行大量的反三角函数计算，既耗时又消耗计算机内存，不利于实时交互。

3 改进的点在多边形内的判断算法

3.1 改进的射线求交法

结合矢量数据特点，对点在多边形内的判断算法进行改进，使得当点位于一个多边形时可以检索到其关联多边形，或者当点位于空洞多边形时，判断点不在多边形中，改进算法主要步骤如下：

Step1：当一个矢量要素包含多个多边形时，分离一个矢量要素中的所有几何体，并遍历所有几何体；

五是建立了社会监督制度。制定下发了 《天津市河道水生态环境社会监督员聘请与管理办法》《实行 “河长制”管理的河道“河长”公示牌设立工作要求》，全市共聘请社会监督员290名，设立河长公示牌400个。向社会公布监督电话，共受理河道水环境社会监督投诉事项34件，办结率100%。

Step2：设包含鼠标点击处的多边形数目为n，对于每个分离出来的多边形都利用射线求交法进行判断，当点位于该多边形内时，n加1；

Step3：只有当n=1时才认为该矢量要素被选中，返回其要素编号。

该改进方法将矢量要素解耦，得到多个无关联的多边形，继而分别判断多边形与点的几何关系。对于分离多边形，鼠标点击位置只可能在一个多边形中，而对于有空洞的多边形，点击处可能落在空洞多边形中，导致n大于1，只有当n为1时才代表点落在外围的多边形中且不在空洞多边形中。

3.2 基于半平面连续链的新型内角和算法

(1)基本概念。

引入半平面连续链[14]的概念，以检测点Q为参考坐标系原点，在多边形P中，位于点Q右边的顶点组成的多边形链称为相对于Q点的右半平面连续链；位于点Q左边的顶点组成的多边形链称为相对于Q点的左半平面连续链；位于点Q上边的顶点组成的多边形链称为相对于Q点的上半平面连续链；位于点Q下边的顶点组成的多边形链称为相对于Q点的下半平面连续链，如图2所示。

图2 半平面连续链

文献[14]已证明引理：对于简单多边形的半平面连续链Lk～k+m，点Q与Lk～k+m上的每个边界的夹角之和等于点Q与Lk～k+m上的两个端点夹角，即Δθ(Lk～k+m)=∠PkQPk+m=Δθ(PkPk+m)。

(2)算法改进。

有了上述引理的理论基础，可对多边形内角和算法进行改进，不需要针对多边形的每条边界都计算边界内角，而只需将多边形P分割成n条半平面连续链。如图2中，竖直的虚线将多边形P分成了左右半平面连续链，横向的虚线将多边形P分成了上下半平面连续链。

相邻多边形链的相邻顶点与Q的夹角的计算方法为：

多边形内角即为所有多边形链内角与相邻多边形链的相邻顶点与点Q的夹角之和，以图2中多边形为例，则多边形内角为：

∑Δθ(P)=Δθ(L2～5)+Δθ(L6～9)+Δθ(L10～11)+Δθ(L12～1)+∠P1QP2+∠P5QP6+ ∠P9QP10+∠P11QP12

(7)

若∑Δθ(P)=0，则点Q位于多边形P外，否则，点Q位于多边形P内。

4 实 验

4.1 实验环境

实验环境：Intel® Core(TM) i5 CPU、1.9 GHz、内存8 GB，操作系统为Windows 7，开发环境为Visual Studio 2013，利用C++实现。实验数据采用格式为shapefile的矢量数据。

4.2 三维场景下栅格化矢量地图拾取可视化效果

图3为几何法和纹理法渲染某地区矢量时矢量要素的拾取可视化效果。可见，在二维矢量与三维地形的融合过程中，几何法的渲染结果出现了断线情况，而纹理法未出现。图3为文中算法在拾取彼此分离或有空洞的矢量要素时的可视化效果，验证了算法同样适用于特殊矢量要素。

图3 矢量要素的拾取可视化效果

4.3 矢量要素拾取效率对比

以三种不同复杂度的面型矢量为实验数据，进行拾取响应时间测试实验，拾取响应时间定义为在屏幕上点击后到相应矢量要素高亮显示的时间。图4为三种不同复杂度的矢量数据分别使用文中改进的射线求交法、新型内角和算法的拾取响应时间。

图4(a)为复杂度最低的矢量的拾取响应时间，可见射线求交法的拾取效率远比新型内角和算法高，这是因为当要素数目较少时，内角和算法需要计算反正切函数，消耗时间较长，而射线求交法的计算次数较少；当矢量复杂度上升时，由图4(b)与(c)可知，新型内角和算法的拾取响应时间基本维持不变，在0.2～0.3 s之间，而射线求交法的拾取响应时间逐渐提升，当矢量数据较复杂时，拾取响应时间在1.2 s左右。实验结果表明：对于常用的矢量数据而言，改进的射线求交法的拾取响应时间在几十毫秒左右，可以供用户使用，而当矢量数据复杂度提升时，新型内角和算法拾取效率更高，满足用户实时性需求。

图4 三种不同复杂度的矢量数据拾取响应时间

4.4 内角和算法改进前后复杂度分析

对于一个顶点数为N的多边形P而言，普通的内角和算法需要计算N次反正切函数、N次二维向量叉乘、N次二维向量点乘以及N次二维向量求模函数。当使用改进的内角和算法时，假设将多边形P分成n条半平面连续链，则由式(5)、(6)可知，此时需要计算2n次反正切函数、2n次二维向量叉乘、2n次二维向量点乘以及2n次二维向量求模函数。对于实际矢量要素中的多边形而言，N远大于2n。因此，在对普通内角和算法改进后，判断点在多边形内的效率得到大幅提升。

对于不同数目顶点的多边形，使用传统的内角和算法和改进的内角和算法，程序响应时间如图5所示。

图5 内角和算法改进前后响应时间对比

可见，当多边形顶点数目较小时，改进的内角和算法效率提升得不明显，当顶点数目较大时，改进的内角和算法的计算效率明显比传统的内角和算法高，而且当顶点数目在5 000以上时，传统的内角和算法所需的时间过长，不适合实时拾取，而改进的内角和算法能满足实时拾取的要求。

5 结束语

文中设计了一种栅格化矢量地图的交互方法，基于实际面型矢量顶点数目多、多边形分离、空洞多边形等特性，改进了传统的射线求交判断点是否在多边形内的算法；同时，提出了一种基于半平面连续链的新型内角和算法，实现了栅格化矢量地图的拾取交互。通过对三种复杂度不同的矢量进行拾取实验后，验证了所提算法的有效性。实验结果表明，该算法拾取效率良好，且拾取响应时间只取决于矢量数据本身的复杂度，与三维地形复杂度无关，可以供三维GIS使用。

[1]YangL,ZhangLQ,KangZZ,etal.Anefficientrenderingmethodforlargevectordataonlargeterrainmodels[J].ScienceChinaInformationSciences,2010,53(6):1122-1129.

[2]KerstingO,DöllnerJ.Interactive3DvisualizationofvectordatainGIS[C]//ProceedingsoftheACMworkshoponadvancesingeographicinformationsystems.NewYork,NY,USA:AssociationforComputingMachinery,2002:107-112.

[3] 康 来,赵 健,宋汉辰,等.面向二维GIS矢量数据三维可视化的地形匹配技术研究[J].计算机科学,2009,36(11):262-265.

[4] 孙文彬,单士刚,白建军,等.实时栅格化的全球矢量数据可视化及交互操作[J].中国矿业大学学报,2013,42(5):845-850.

[5]ZhiY,GaoY,WuL.Animprovedalgorithmforvectordatarenderinginvirtualterrainvisualization[C]//Procof2013 21stinternationalconferenceonIEEE.[s.l.]:IEEE,2013.

[6]WangX,LiuJ,BiJ.Renderingofvectordataon3Dvirtuallandscapes[C]//Procof2009 1stinternationalconferenceoninformationscienceandengineering.Piscataway,NJ,USA:IEEEComputerSociety,2009:2125-2128.

[7]SunW,ShanS,FengC.Geometry-basedmappingofvectordataandDEMbasedonhierarchicallongitude/latitudegrids[C]//Procof2010 2ndinternationalconferenceongeoscienceandremotesensing.Piscataway,NJ,USA:IEEEComputerSociety,2010:215-218.

[8]WangS,ZhongE,LuH.Aneffectivealgorithmforlinesandpolygonsoverlayanalysisusinguniformspatialgridindexing[C]//Procof2015 2ndIEEEinternationalconferenceonspatialdataminingandgeographicalknowledgeservices.Piscataway,NJ,USA:IEEEComputerSociety,2015:175-179.

[9]ZhangX,SuiZ,WuL.Aprocessingandschedulingmethodforvectorrenderinginglobal3DGIS[C]//Procof2011 19thinternationalconferenceongeoinformatics.[s.l.]:IEEE,2011.

[10] 李 融,郑文庭.三维地形高质量实时矢量叠加绘制[J].计算机辅助设计与图形学学报,2011,23(7):1106-1114.

[11]XuY,SuiZ,WengJ.Visualizationmethodsofvectordataonadigitalearthsystem[C]//Procof2010 18thinternationalconferenceongeoinformatics.Piscataway,NJ,USA:IEEEComputerSociety,2010:1-5.

[12] 陈 鸿,汤晓安,谢耀华,等.基于视点相关透视纹理的矢量数据在三维地形上的叠加绘制[J].计算机辅助设计与图形学学报,2010,22(5):753-761.

[13]DingJ,WangQ,WuK,etal.ThestudyofrobustalgorithmfororientationandpointinclusionqueryforpolygoninGIS[C]//Procof2011internationalconferenceonremotesensing,environmentandtransportationengineering.Piscataway,NJ,USA:IEEEComputerSociety,2011:2756-2760.

[14] 丁 健.基于GIS的野战给水保障辅助决策关键算法研究[D].北京:中国科学院研究生院,2005.

A Picking Interaction Method of Rasterized Vector Map

YU Xin1,GUO Yu1,WANG Yang2

(1.Department of Automation,Nanjing University of Science and Technology,Nanjing 210094,China; 2.Institute of Electronics of Chinese Academy of Sciences,Suzhou 215000,China)

Aiming at the problem that the vector map rendered based on texture is difficult to realize the interaction,an interactive method of the rasterized vector map is designed.Based on the characteristic of polygonal vector which has a great quantity of vertices,separate polygon and holey polygon,the traditional ray intersection method determining whether a point is in a polygon is improved to apply to polygonal vector.Meanwhile,an interior angle summation based on half-plane continuous chain which could reduce the computation of the traditional interior algorithm is proposed.The experiment is done by using vector data with different degrees of complexity.The result shows that the efficiency of rendering based on rasterization is significantly increased and the bad overlaying performance of vector rendering in 3D scene is improved.Vector map interaction could be realized in this case.The proposed interaction method which is only according to the degrees of complexity of vector data and has nothing to do with the degrees of complexity of terrain,guarantees favorable performance of real-time to meet the need of GIS.

vector map interaction;feature picking;rasterization;ray-intersection;interior angle summation

2015-12-27

2016-04-21

时间：2016-09-19

国家自然科学基金资助项目(61473152)；南京理工大学研究生创新实践计划项目

俞 信(1991-)，男，硕士研究生，研究方向为时空大数据可视化技术；郭 毓，教授，博士，研究方向为智能控制、图像处理。

http://www.cnki.net/kcms/detail/61.1450.TP.20160919.0839.020.html

TP301

A

1673-629X(2016)10-0118-05

10.3969/j.issn.1673-629X.2016.10.026