一类乘性有理样条权函数神经网络灵敏度分析
张代远,王雷雷
(1.南京邮电大学 计算机学院,江苏 南京 210003;2.江苏省无线传感网高技术研究重点实验室,江苏 南京 210003;3.南京邮电大学 计算机技术研究所,江苏 南京 210003)
一类乘性有理样条权函数神经网络灵敏度分析
张代远1,2,3,王雷雷1
(1.南京邮电大学 计算机学院,江苏 南京 210003;2.江苏省无线传感网高技术研究重点实验室,江苏 南京 210003;3.南京邮电大学 计算机技术研究所,江苏 南京 210003)
样条权函数神经网络是一种新型的神经网络,它克服了传统神经网络收敛速度慢、初值敏感、局部极小的问题。因其能精确学习给定的样本,并且结构简单、训练速度快,因此被广泛关注。结合分子三次、分母一次的有理样条函数和样条权函数神经网络的优势,研究了分子三次、分母一次乘性有理样条权函数神经网络,并对其灵敏度进行了理论分析和实验仿真。通过理论分析和仿真可以看出,该神经网络具有分子三次、分母一次的有理样条和样条权函数神经网络的优越特性,在一定扰动范围内,该样条权函数神经网络的灵敏度稳定,具有很强的抗干扰能力。
样条权函数;样条插值;神经网络;灵敏度分析
0 引 言
随着云计算、机器学习和大数据计算的蓬勃兴起,人工神经网络理论和方法得到了更加广泛的关注和应用。但是传统的BP算法往往存在局部极小、不收敛或者收敛速度慢、初值敏感等缺陷。这些缺陷极大限制了神经网络在实际工程中的应用。许多学者对传统的BP算法进行了多方面的改进,比如采用遗传算法调整网络参数[1],优化初始权值或者其他参数[2]等。但是这些改进无法从根本上克服梯度下降类算法的缺点。文献[3]提出了新的神经网络(样条权函数神经网络)及其训练算法,该算法能够精确学习给定的样本,克服了传统算法(如BP算法等)存在的局部极小、收敛速度慢、初值敏感等缺点。由于样条插值在曲线和平面设计中的重要作用,许多学者对其进行了大量研究[4-5],发现分子三次、分母一次的有理样条[6]能够很好地逼近目标函数,而且通过选取适当参数可以使其获得很好的形状控制能力[7]。
当输入样本或者权值存在扰动时,样条权函数神经网络的输出会发生变化。从理论上分析这些变化对于整个网络系统产生的影响是很重要的。灵敏度作为神经网络的一个重要指标,可以分析这些变化给系统带来的影响,而且有不少学者对灵敏度或者神经网络灵敏度做过分析[8-11]。文中结合分子三次、分母一次的有理样条函数和样条权函数神经网络的优势,研究分子三次、分母一次乘性有理样条权函数神经网络,利用文献[10]中对灵敏度的定义,对其灵敏度进行了分析。该神经网络具有分子三次、分母一次的有理样条和样条权函数神经网络的优越特性,可以被广泛应用到工程实践中。
1 分子三次、分母一次乘性有理样条权函数神经网络
文献[3]提出的样条权函数神经网络,只有两层。为了简单起见,这里引用多输入单输出的乘性样条权函数神经网络结构,如图1所示。其中输入样本向量是m维,因此输入端有m个节点,每个输入端节点通过连接权前馈连接到所有乘法单元。对于多输入多神经输出网络,可以得到类似的网络结构[3]。

图1 多输入单输出乘性样条权函数神经网络结构
从图中可以看出,输入向量x有m维,其中xi,i=1,2,…,m为m维输入向量的第i个分量。假设有N+2个训练样本,则xi的向量表示为:
(1)
那么对应输出节点的向量表示为:
(2)
(3)
乘积因子ρi表示每一个输入端节点对相应输出的贡献大小,ρi越大说明输入节点在网络训练中对输出的影响越大。近似权函数si(xi)由输入向量xi和输出向量fi决定,所以对应的插值点为:
(4)
既然已经得到了插值点,那么就可以通过数学上的插值方法精确通过这些插值点(样本点),所以说权函数神经网络是精确学习算法,就是说经过训练的网络能够精确“回想”起已经学过的样本。
插值理论方法丰富多彩,考虑到实际样本可能会在极点附近,或者一些应用中需要考虑形状控制时,有理函数具有一定的优势。因此文中采用分子三次、分母一次有理样条函数作为权函数,这与文献[3]所采用的插值多项式是不同的。
根据文献[6-7],对分子三次、分母一次有理样条函数给出如下定义:

(5)
(6)
(7)
其中
(8)
(9)
Δp=(fp+1-fp)/hp,αp,βp>0,为形状控制参数。
2 分子三次、分母一次乘性有理样条权函数神经网络灵敏度分析
2.1 灵敏度的统计学定义
对图1所示的神经网络,统计灵敏度定义[10]为:
(10)

对于多个输入样本,假设第p个输入样本的灵敏度为Sp,p=0,1,…,N+1,通常,可以采用以下两种方式来评价神经网络的统计灵敏度。
采用所有样本中的最大灵敏度:
(11)
采用所有样本的平均灵敏度:
(12)
2.2 模型逼近误差和逼近噪声误差分析
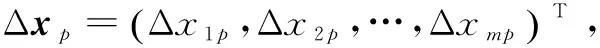
(13)
根据上述的神经网络理论噪音误差输出值的运算方法,对网络输出值的理论噪音误差进行具体分析。
先考虑输出层第j个神经元理论噪音输出误差。同样地,假设第p个不含噪声的标准输入样本为
在这种输入情况下,第j个神经元的理论输出值为:
(14)
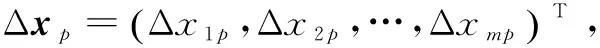
则第j个神经元的理论噪音输出误差为:


(17)

因为δip→0,所以
(18)
因此可得:
(19)
将Dip,Fip,δip代入式(19)可得:
(20)

(21)
而对于多输入多输出乘性样条权函数逼近噪声误差的表达式,可以由式(21)增加反映输出节点序号的加下标j表示。

(22)
因此可得:
显然,根据式(13)可知,多输入多输出的输出层误差可以表示成如下的矩阵形式:
(24)
此时可以将式(11)或式(12)中增加反映式(24)中行、列的下标即可。这样可以得到多维输出神经网络灵敏度,因此根据式(10)、(11)、(12)、(24)就可以计算出分子三次、分母一次乘性有理样条权函数神经网络的统计灵敏度。
3 仿真实验
下面进行数值仿真实验,验证分子三次、分母一次乘性有理样条权函数的灵敏度稳定性。
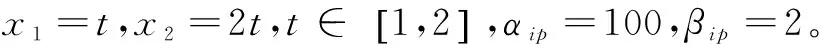
R=(Y*-Y)/Y
(25)
其中,Y*表示没有扰动时的输出;Y表示有扰动时的目标输出。
灵敏度的实际仿真值采用数理统计[13]的方法求得,对不同组的扰动利用式(21)计算网络输出层误差,然后再统计出扰动的标准差和网络输出层误差的方差,按照式(10)计算灵敏度仿真值。平均相对误差曲线和灵敏度曲线分别如图2和图3所示。

图2 平均相对误差曲线(学习曲线为x1=t,x2=2t)

图3 灵敏度曲线(学习曲线为x1=t,x2=2t)

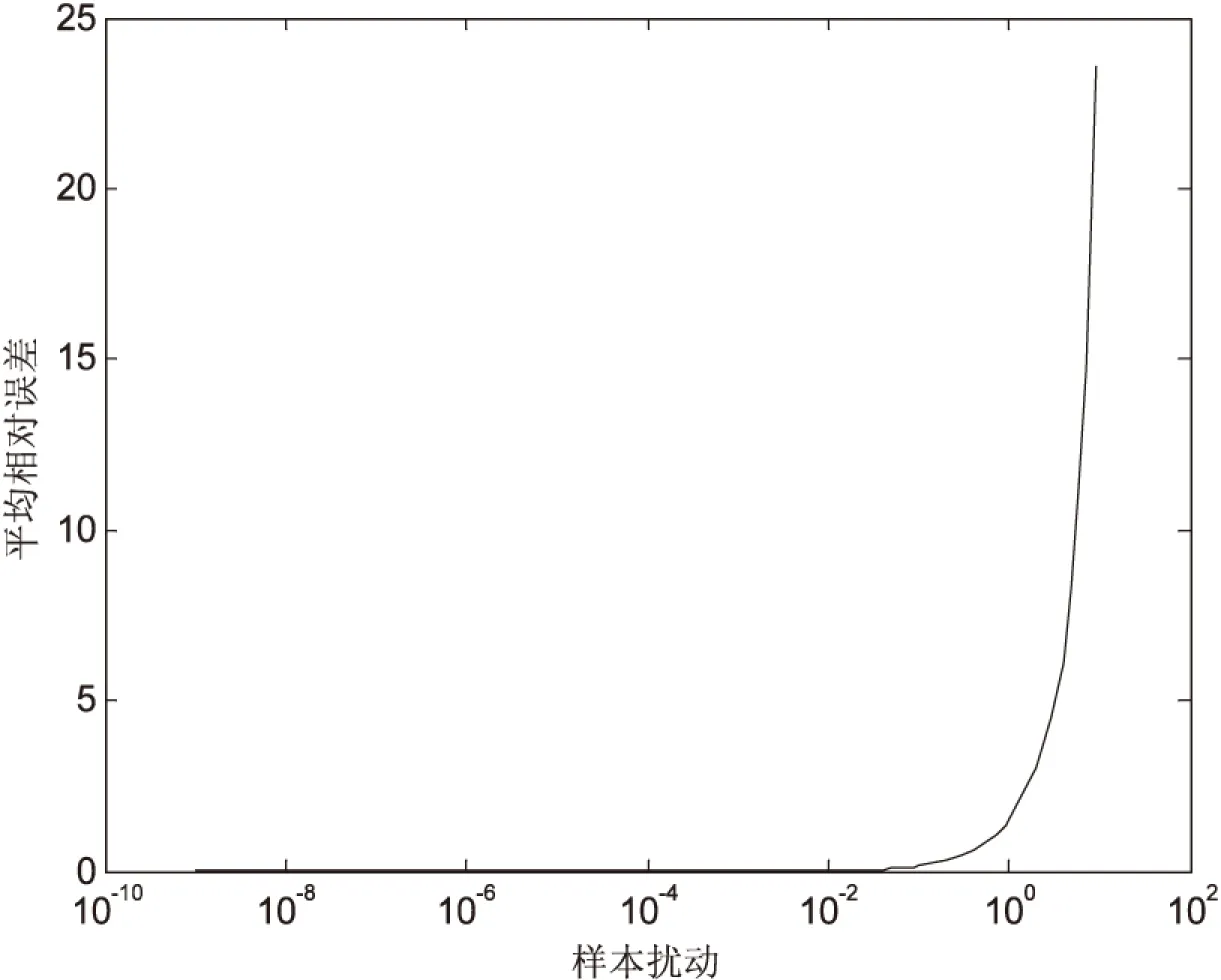
图4 平均相对误差曲线(学习曲线为x1=t2,x2=sin0.5t)

图5 灵敏度曲线(学习曲线为x1=t2,x2=sin0.5t)

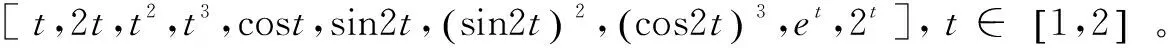
输入维数对平均相对误差的影响如表1所示。

表1 输入维数对平均相对误差的影响
从表1可以看出,当输入维数m≤1 000时,平均相对误差非常小,即Z*非常接近Z。而根据UCIrvineMachineLearningRepository的数据,92%的数据集输入属性个数小于1 000,因此式(21)具有实用性和代表性。
4 结束语
文中将样条权函数神经网络和分子三次、分母一次的有理样条相结合,研究分子三次、分母一次乘性有理样条权函数神经网络灵敏度。通过理论分析和仿真实验,表明当扰动在较宽的变化范围内,灵敏度值非常稳定。在此扰动范围内神经网络的仿真输出与目标样本的理论输出偏差很小,能与目标样本较好匹配。说明当样本扰动在一定范围内时,分子三次、分母一次乘性有理样条权函数神经网络的网络泛化能力[14]不会受到外界噪声的影响,即具有较强的抗干扰能力,可以广泛应用于工程实践的各个领域。
[1]KhashmanA.Amodifiedbackpropagationlearningalgorithmwithaddedemotionalcoefficients[J].IEEETransactionsonNeuralNetworks,2008,19(11):1896-1909.
[2]WedgeD,IngramD,McLeanD,etal.Onglobal-localartificialneuralnetworksforfunctionapproximation[J].IEEETransactionsonNeuralNetworks,2006,17(4):942-952.
[3] 张代远.神经网络新理论与方法[M].北京:清华大学出版社,2006.
[4]SunQ,BaoF,DuanQ.Shape-preservingweightedrationalcubicinterpolation[J].JournalofComputationalInformationSystems,2012,8(18):7721-7728.
[5]BaoF,SunQ,DuanQ.Pointcontroloftheinterpolatingcurvewitharationalcubicspline[J].JournalofVisualCommunication&ImageRepresentation,2009,20(4):275-280.
[6]DuanQ,DjidjeliK,PriceWG,etal.Arationalcubicsplinebasedonfunctionvalues[J].Computers&Graphics,1998,22(4):479-486.
[7]DuanQ,DjidjeliK,PriceWG,etal.Weightedrationalcubicsplineinterpolationanditsapplication[J].JournalofComputational&AppliedMathematics,2000,117(2):121-135.
[8] 张代远.零代价函数条件下的前馈神经网络统计灵敏度分析[J].模式识别与人工智能,2004,17(4):510-515.
[9]ZhangD.Anewalgorithmoftrainingneuralnetworksbyorthogonalweightfunctionsandsensitivityanalysis[C]//Procof2012IEEE5thinternationalconferenceonadvancedcomputationalintelligence.[s.l.]:IEEE,2012:324-327.
[10]ChoiJY,ChoiCH.Sensitivityanalysisofmultilayerperceptronwithdifferentiableactivationfunctions[J].IEEETransactionsonNeuralNetworks,1992,3(1):101-107.
[11]LiCG,LiHF,ZhangYF,etal.Sensitivityanalysisofmultilayerperceptronbasedonelasticfunction[C]//Procofinternationalconferenceonmachinelearningandcybernetics.[s.l.]:IEEE,2010:1490-1493.
[12]ZhangDY,WangLL.Erroranalysisofneuralnetworkwithmultiplyneuronsusingrationalsplineweightfunctions[J].AppliedMechanicsandMaterials,2015,713-715:1716-1720.
[13]NgWWY,YeungDS,RanQ,etal.Statisticaloutputsensitivitytoinputandweightperturbationsofradialbasisfunctionneuralnetworks[C]//ProcofIEEEinternationalconferenceonsystems,manandcybernetics.[s.l.]:IEEE,2002:503-508.
[14]ZhangDY.Analysisofgeneralizationforanewkindofneuralnetwork[J].AdvancedMaterialsResearch,2013,760-762:2023-2027.
Sensitivity Analysis of Neural Network with Rational Spline Weight Functions Using Multiplicative Neurons
ZHANG Dai-yuan1,2,3,WANG Lei-lei1
(1.College of Computer,Nanjing University of Posts and Telecommunications,Nanjing 210003,China;2.Key Laboratory of Jiangsu High Technology Research for Wireless Sensor Networks,Nanjing 210003,China;3.Institute of Computer Technology,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
The neural network with spline weight function is a new kind of neural network,which overcomes many problems such as slow convergence speed,sensitive to initial value and local minima.It is widely concerned because of its accurate learning approach to given patterns,simple network topology,fast training speed and so on.Based on the advantage of neural network with spline weight function,the sensitivity of neural network with cubic numerator and linear denominator of rational spline weight functions using multiplicative neurons is discussed,and the accuracy of analytical results is verified by simulation.Both the theoretical analysis and simulation results show that when the disturbance is in a certain range,the sensitivity of this kind of spline weight function neural network is very stable,and is featured with strong noise resistance.
spline weight function;spline interpolation;neural network;sensitivity analysis
2016-01-05
2016-05-12
时间:2016-09-19
江苏高校优势学科建设工程资助项目(yx002001)
张代远(1957-),男,教授,博士,硕士生导师,研究方向为人工智能、计算机体系结构、计算机应用等;王雷雷(1991-),男,硕士研究生,研究方向为智能计算技术与应用。
http://www.cnki.net/kcms/detail/61.1450.TP.20160919.0841.038.html
TP301
A
1673-629X(2016)10-0050-05
10.3969/j.issn.1673-629X.2016.10.011

