幅相控制精度对射频仿真目标位置误差的影响*
武鹏飞,何秋茹
(北京仿真中心 航天系统仿真实验室,北京 100854)
仿真技术
幅相控制精度对射频仿真目标位置误差的影响*
武鹏飞,何秋茹
(北京仿真中心 航天系统仿真实验室,北京 100854)
在射频仿真系统中,目标的精确位置是通过对三元组辐射信号的幅度和相位控制来实现的,幅度和相位控制精度直接影响目标位置的模拟精度。基于波因廷矢量法建立了三元组合成位置模型,以两元组为例,分析了二元组合成位置特性及其对幅度和相位的灵敏度特性,建立了合成位置误差与幅相控制精度关系的数学模型,并给出了合成位置误差的分布规律,结论具有工程指导意义。
射频仿真;三元组;波因廷矢量;目标位置误差;幅度灵敏度;相位灵敏度
0 引言
随着精确制导技术的发展,对具有多散射中心的复杂体目标与分布式杂波的仿真已经成为射频仿真试验的重要任务[1]。这就要求射频仿真系统具备模拟多个等效辐射中心的能力。但是现有的系统在单通道中同一时间只能模拟一个等效辐射中心[2-3]。为此,国内学者在这方面进行了深入研究,提出了引入相位控制,增加控制维数的解决方案。
引入三元组相位信息的控制方法是一种全新的阵列控制方法,其性能直接影响到仿真试验精度,进而影响到被试设备的故障甄别和结论鉴定。所以,分析新方法中幅相控制精度对辐射中心位置误差的影响,验证该方法的可行性很有必要。
本文详细推导了三元组合成位置模型。在此基础上以二元组为例,分析了模型的合成位置特性及其对幅度、相位的灵敏度特性,建立了合成位置误差与幅度、相位控制精度关系的数学模型。最后,通过大量的仿真计算,分别给出了幅度控制精度和相位控制精度对目标位置误差的影响及其误差分布特性,以期作为工程实践的参考。
1 三元组合成位置模型
三元组合成模型建立了三元组天线辐射信号的幅度、相位与所需模拟目标的球坐标的对应关系,是目标模拟的关键[4]。
如图1所示建立坐标系,阵列球坐标系原点为O,x轴水平指向目标阵列的中心OA;y轴垂直向上;z轴按右手直角坐标系来确定[5]。
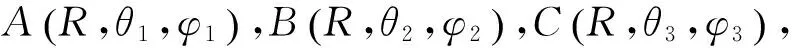
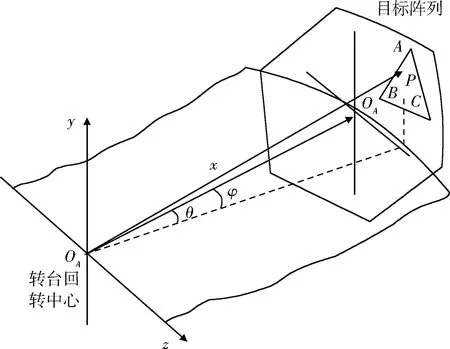
图1 转台坐标系[8]Fig.1 Table coordinate system
若三元组3个天线A,B,C辐射信号的幅度与初始相位分别为E1,E2,E3和ψ1,ψ2,ψ3,则三元组三个天线辐射信号在三轴转台回转中心处的电场可表示为[9-10]:
(1)
磁场可表示为
(2)
其中,球坐标系下的单位向量与直角坐标系下的单位向量的转化关系如下[11]:
(3)
设E总和H总为3元组三个天线辐射信号在三轴回转中心处的合成场,满足矢量叠加原理[7-8],则波因廷矢量可表示为[5]
(4)
令βi=ψi-kR,将式(1)和(2)通过式(3)化为直角坐标系下的表达式,然后带入式(4)中化简,可表示为[9]
(5)
式中:X,Y,Z可表示为
(6)
(7)
(8)
根据几何关系[12-13],可得
(9)
(10)
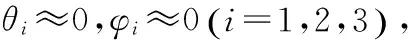
(11)
(12)
式(11)和(12)即为三元组合成位置模型的表达式。
2 目标位置的幅度、相位灵敏度分析
2.1 幅度、相位灵敏度定义
为了分析幅度、相位控制精度对目标位置误差的影响,首先分析目标位置的幅度、相位灵敏度特性。根据灵敏度定义[14-15]可知,目标高低角和方位角的幅度灵敏度表达式为
(13)
目标高低角和方位角的相位灵敏度表达式为
(14)
因此,本文首先从二元组入手,结合解析表达式与等高线分析目标位置的幅度、相位灵敏度特性,然后将其特性扩展到三元组,建立合成位置误差与幅相控制精度关系的数学模型。
2.2 二元组目标位置特性
以高低角θ通道为例,二元组合成位置的表达式为
(15)
式中:δ=ψ1-ψ2,表示2个辐射信号的相位差。
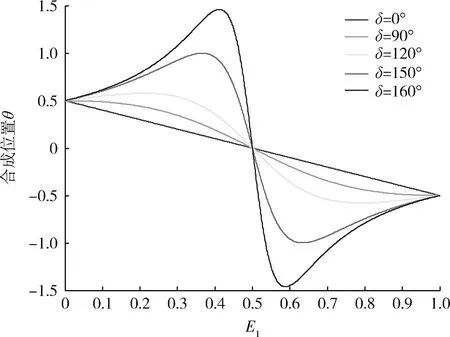
图2 合成位置与幅度相位的对应关系Fig.2 Relationship between location and the control of amplitudes and phases
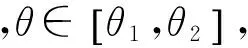
2.3 目标位置的幅度灵敏度特性
合成位置θ相对于幅度E1灵敏度表达式为
(16)
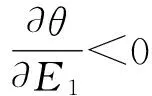
(17)
由此可知,若目标位置位于二元组外部,则存在一个相位差使得目标位置的幅度灵敏度为零。
在单元间距归一化和二元组幅度归一化条件下,作目标位置为0.1~1.0的10条等高线和幅度灵敏度为-0.1~0.1的11条等高线,如图3所示。
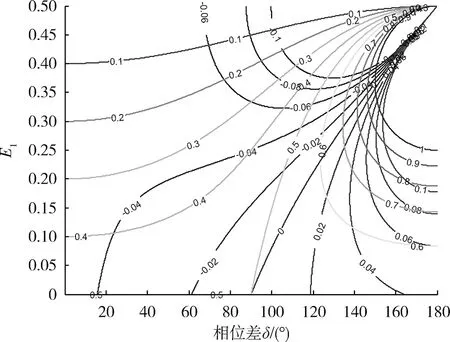
图3 目标位置和幅度灵敏度的等高线Fig.3 Contour lines of target position and amplitude sensitivity
2.4 目标位置的相位灵敏度特性
合成位置θ相对于相位差δ灵敏度表达式为
(18)
特别的,当E1=E2,即目标位置位于二元组连线的中点时,当E1=0或E2=0,即目标位置位于二元组辐射单元上时,目标位置的相位灵敏度恒为0。
在单元间距归一化和二元组幅度归一化条件下,作目标位置为0.1~1.0的10条等高线和相位灵敏度为0~0.05的10条等高线,如图4所示。
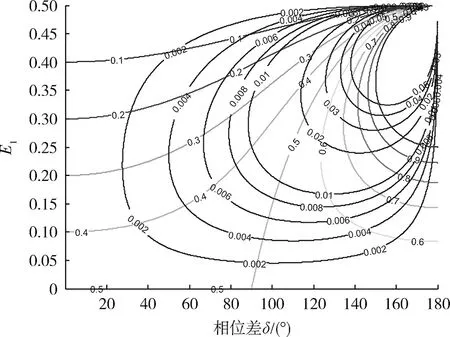
图4 目标位置和相位灵敏度的等高线Fig.4 Contour lines of target position and phase sensitivity
显然,合成位置的相位灵敏度为0的等高线为图中四条边(E1=0,E1=0.5,δ=0°,δ=180°)构成的矩形,即在相位灵敏度零点的表达式中,幅度和相位是相互独立的。除合成位置位于二元组端点以及中点的特殊情况以外,若合成位置位于二元组内部,合成位置的相位灵敏度的零点为δ=0°;若合成位置位于二元组外部,相位灵敏度的零点为δ=180°。
3 幅、相控制精度对目标位置误差的影响
3.1 幅度控制精度对目标位置误差的影响

(19)
将式(13)代入式(19),从二元组合成位置的幅度灵敏度特性入手,根据三元组和二元组的相似性,建立三元组合成位置误差与幅度控制精度关系的数学模型,用数值计算的方法得出合成位置误差的分布数据,以此分析幅度控制精度对目标位置误差的影响。

设幅度控制最大误差0.5 dB,相位控制最大误差为0°,将方位角误差、高低角误差以及目标位置误差分布数据作等高线分析,如图5~7所示。
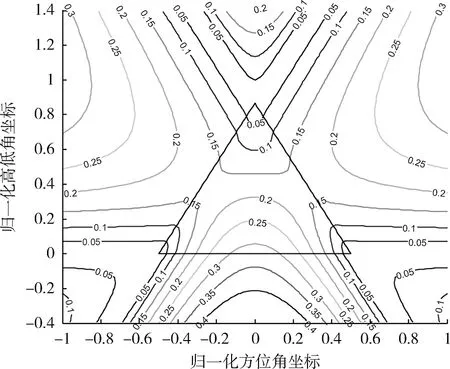
图5 幅度控制精度引起的方位角φ误差等高线分布图Fig.5 Contour lines of azimuth angle φ error generated by amplitude control precision
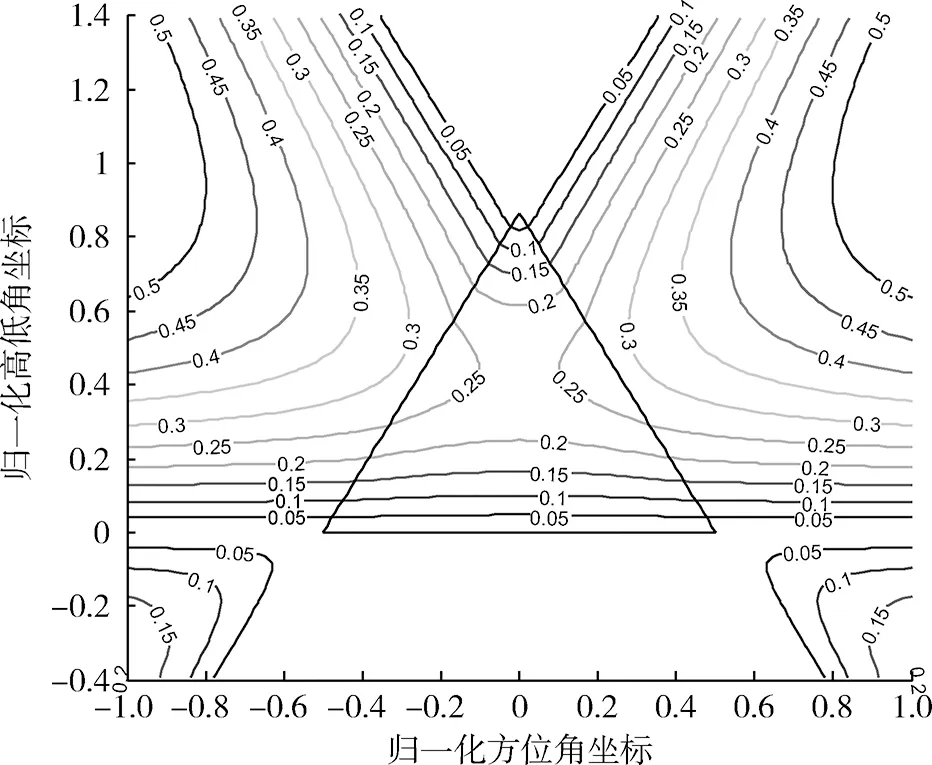
图6 幅度控制精度引起的高低角θ误差等高线分布图Fig.6 Contour lines of altitude angle θ error generated by amplitude control precision

图7 幅度控制精度引起的目标位置误差等高线分布图Fig.7 Contour lines of target position error generated by amplitude control precision
从式(19)和图5~7中可以看出:
(1) 由幅度控制精度引起的目标位置误差大小与三元组各辐射单元的相对位置有关,且目标位置误差大小与三元组单元间距成正比。
(2) 在三元组内部,若目标位于三元组底边中点(即方位角通道中点),由幅度控制精度引起的方位角误差最大;若目标位于三元组高线中点(即高低角通道中点),由幅度控制精度引起的高低角误差最大;若目标位于三元组重心,由幅度控制精度引起的目标位置误差最大。若目标位于三元组顶点,则由幅度控制精度引起的方位角误差、高低角误差、目标位置误差均为最小。
(3) 当目标位于三元组外时,由幅度控制精度引起的目标位置误差分布呈对称性。根据误差分布等高线可将三元组外的区域划分为6个子区域,其中,三元组顶点所对子区域的目标位置误差明显小于三元组各边所对子区域的目标位置误差。在同一子区域,目标位置误差随着目标与三元组距离的增大而增大。
3.2 相位控制精度对目标位置误差的影响
(20)
将式(14)代入式(20),同理,从二元组合成位置的相位灵敏度特性入手,建立合成位置误差与相位控制精度关系的数学模型,用数值计算的方法给出合成位置误差的分布数据,以此分析相位控制精度对目标位置误差的影响。
设相位控制最大误差为5°,幅度控制最大误差0 dB,在三元组归一化坐标系中,将方位角误差、高低角误差以及目标位置误差分布数据作等高线分析,如图8~10所示。
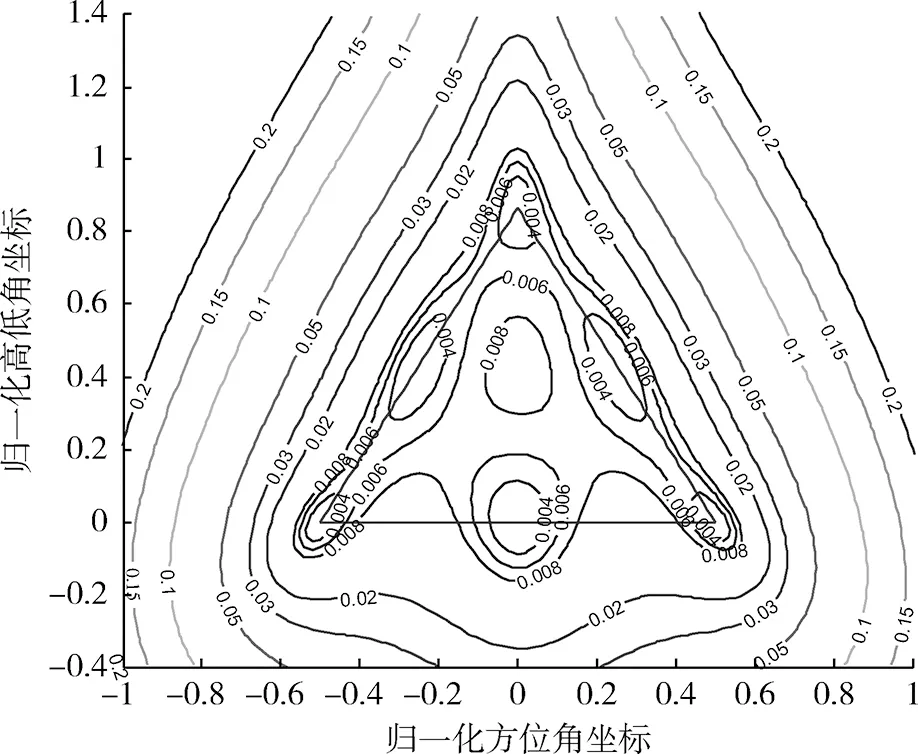
图8 相位控制精度引起的方位角φ误差等高线分布图Fig.8 Contour lines of azimuth angle φ error generated by phase control precision
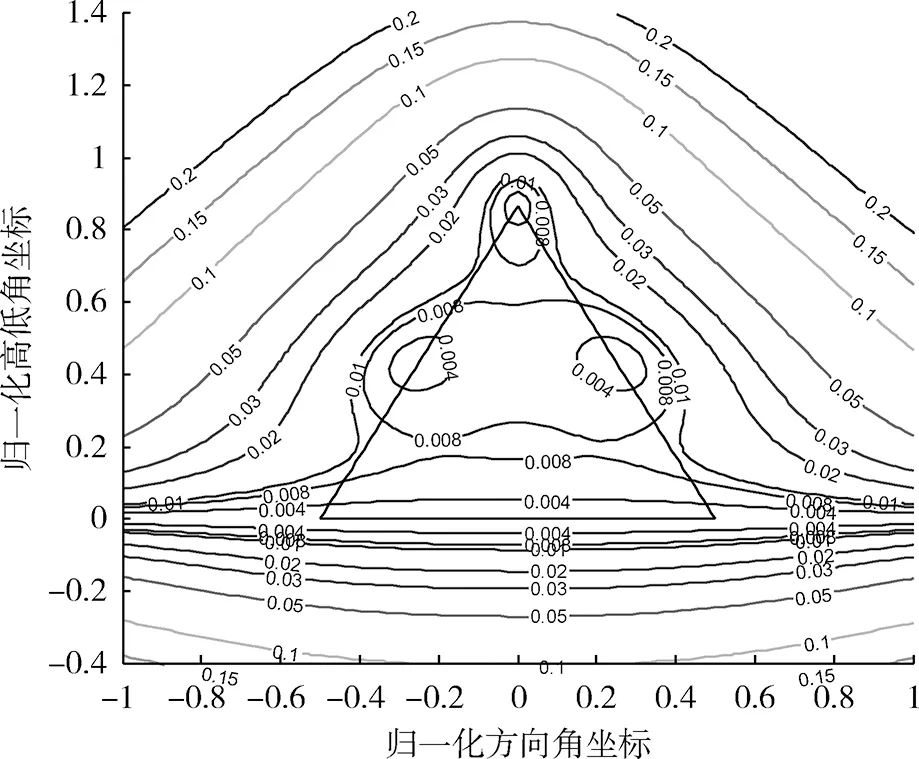
图9 相位控制精度引起的高低角θ误差分布图Fig.9 Contour lines of altitude angle θ error generated by phase control precision
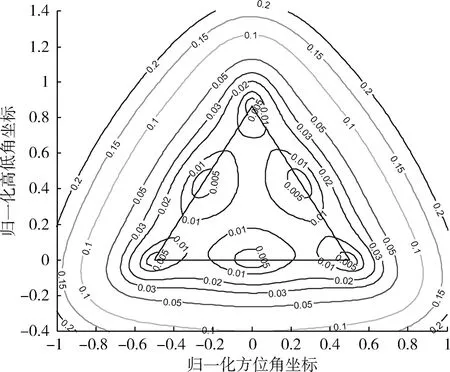
图10 相位控制精度引起的目标位置误差等高线分布图Fig.10 Contour lines of target position error generated by phase control precision
从式(20)和图8~10中可以看出:
(1) 由相位控制精度引起的目标位置误差大小与三元组各辐射单元的相对位置有关,且标位置误差大小与三元组单元间距成正比。
(2) 在三元组内部,若目标位于三元组重心,由相位控制精度引起的目标位置误差最大;若目标位于三元组顶点以及各边中点,由相位控制精度引起的方位角误差、高低角误差以及目标位置误差均为最小。
(3) 当目标位于三元组外时,由相位控制精度引起的目标位置误差分布呈连续性,随着目标与三元组之间距离的增大,目标位置误差也在增大。
4 结论
本文在三元组合成位置模型的基础上,从二元组出发,分析了二元组合成位置特性及其对幅度和相位的灵敏度特性,分析了幅相控制精度对合成位置误差的关系,经过仿真计算,得到如下结论:
(1) 幅相控制精度引起的目标位置误差大小与三元组单元间距成正比,在工程中三元组单元间距应根据仿真任务中对目标位置精度的要求选取;
(2) 在三元组内部,幅相控制精度引起的目标位置误差分布是连续的。在三元组重心,幅相控制精度引起的目标位置误差最大;在三元组顶点,幅相控制精度引起的目标位置误差最小。在同一位置,由幅度控制精度引起的目标位置误差远大于由相位控制精度引起的目标位置误差。因而在工程中常放宽对相位控制精度的要求,重点提高幅度控制精度。
(3) 当目标位于三元组外时,随着目标与三元组之间距离的增大,幅相控制精度引起的目标位置误差也在增大;在同一位置,由幅度控制精度引起的目标位置误差和由相位控制精度引起的目标位置误差相差不大。所以在工程中,三元组的有效控制范围是有限的,且提高幅度控制精度和提高相位控制精度同等重要。
[1] BISHOP C B. Error Analysis of Point Targets in HWIL Simulation[C]∥1994 SCSC, 1994:373-378.
[2] RUSSELL R F, MASSEY S. Radio Frequency System Simulator[R]. AIAA Paper, 1972:72-861.
[3] 毛继志, 郭陈江, 张麟兮,等. 幅相误差对射频仿真系统目标位置精度的影响[J]. 系统仿真学报, 2003, 15(8):1149-1151. MAO Ji-zhi,GUO Chen-jiang,ZHANG Lin-xi,et al. The Influence of Amplitude and Phase Error for Target Position Error in REFF[J]. Journal of System Simulation,2003, 15(8):1149-1151.
[4] 王泗宏, 黄惠明, 李军,等. 射频仿真幅相控制误差对目标位置精度的影响分析[J]. 飞行器测控学报, 2007(2):59-63. WANG Si-hong,HUANG Hui-ming,LI Jun,et al. Analysis of the Influence of Amplitude and Phase Errors on Target Position Precision in REFF[J]. Journal of Spacecraft TT&C Technology, 2007(2):59-63.
[5] Robert S Elliott. Antenna and Design[R]. Prentic-Hall. Inc., 1981.
[6] JACKSON R, VAMIVAKES A N. An Overview of Hardware-in-the-Loop Simulation for Missiles [R].AIAA,1997.
[7] ZHANG H, WANG J, Yin X. Study on Feed Configurations of Wideband Slot Antenna[C]∥ Microwave Conference, 2008. APMC 2008. Asia-Pacific. IEEE, 2008:1-4.
[8] HOWARD D D.Radar Target Glint in Tracking and Guidance System Based on Echo Signal Phase Distortion[C]∥Proc. NEC,1959,15:840-849.
[9] DUNN J H, HOWARD D D. RADAR Target Amplitude, Angle, and Doppler Scintillation from Analysis of the Echo Signal Propagating in Space[J]. Microwave Theory & Techniques IEEE Transactions on, 1968, 16(9):715-728.
[10] Elliott R S. Antenna Theory and Design[J]. Antenna Theory & Design, 1981, 129(2):B27.
[11] POLKINGHORNE A A. Radio Frequency Simulation System (RFSS) System Design Handbook[R]. Boeing Company D243-10004-1,1975.
[12] BELROSE F. Radio Frequency Simulation System (RFSS) Capabilities Summary[R]. Boeing Company Technical Report, 1982.
[13] LI Hua,ZHOU Jian-jiang,ZHAO Han-wu,et a1.Stealth Treatment of Turntable in Ultra-Wideband Radio Frequency Simulation System[C]∥2010 IEEE International Conference on Ultra-Wideband.IEEE Press,2010:l-4.
[14] GONG Shu-feng,PAN Ming-hai.Influence of Linear Frequency-Modulated and Frequency Agility on Accuracy of Azimuth Simulation of Three-Element-Array[J].Radar & ECM,2010,30(2):18-21.
[15] MASUDA Y,TANABE M,SHINONAGA M.A Simple Method for Estimation of Maximum Spurious Radiation Level from Phased Array Antennas[C]∥2009 ICROS-SICE International Joint Conference.Kawasaki,2009:3042-3046.
Influence of Amplitude and Phase Precision for Target Position Error in RF
WU Peng-fei, HE Qiu-ru
(Beijing Simulation Center,Science and Technology on Spacial System Simulation Laboratory, Beijing 100854,China)
Accurate target position is simulated through the control of radiation signals’ amplitudes and phases in the triad of antennas in the radio frequency simulation. For this reason the control precision of amplitudes and phases directly affects the target position precision. Based on the poyting vector method, the triad of antennas synthetic theoretical model is concluded. For the tuple of antennas, the synthetic theoretical and the sensitivity of amplitudes and phases are analyzed. The mathematical model of the corresponding relationship between synthetic theoretical error and the control precision of amplitudes and phases is concluded. Then, the distribution regularities of synthetic theoretical error are given. The conclusions are of high significance to engineering application.
radio frequency; triad antennas; poyting vector; target position error; amplitudes sensitivity; phases sensitivity
2016-03-14;
2016-06-02
有
武鹏飞(1989-),男,山西朔州人。硕士生,研究方向为控制科学与工程。
10.3969/j.issn.1009-086x.2016.06.028
TJ765.3;TP391.9
A
1009-086X(2016)-06-0167-07
通信地址:100854 北京142信箱30分箱
E-mail:wupf_73@163.com

