有质量弹簧振子的弹簧内力

陈奎孚 黄 峰 蒋 晓 赵建柱

(1中国农业大学理学院,北京 100083; 2北京农业职业学院机电工程学院，北京 102208; 3中国农业大学工学院,北京 100083)

有质量弹簧振子的弹簧内力

陈奎孚1黄 峰1蒋 晓2赵建柱3

(1中国农业大学理学院,北京 100083;2北京农业职业学院机电工程学院，北京 102208;3中国农业大学工学院,北京 100083)

文章分析了有质量弹簧振子的弹簧内力，并用Matlab工具进行图形化展示.分析表明：弹簧质量不可忽略时，弹簧各断面上内力是断面位置的函数；对振子均匀拉伸-释放所建立的振动，弹簧内力随时间的变化规律不再是简谐波；随着弹簧质量的增加，内力偏离简谐波越来越明显；质点质量为零时, 内力随时间的变化规律为周期性方波.

弹簧振子；波动；偏微分方程；内力

弹簧振子是大学物理教学的经典例子.在这个经典例子中，一般都忽略不计弹簧的质量.若与质点相比，弹簧不是很轻，就需要考虑弹簧的质量.弹簧质量必须考虑的弹簧振子本质上是波动问题，研究它的工具变得复杂，相应的物理现象也复杂得多.就该问题，国内已经发表了很多文章[1-8]，朱洪玉对这一问题做了很系统的总结，对相关争议进行了澄清[9].

需要特别指出的是：有些特性，它们在弹簧质量可忽略的情形下是显而易见的，但在波动问题下就不那么直观了.比如，若弹簧质量不计,则其内力并不随弹簧的断面位置而变化(为了表述清晰，我们把弹簧当成圆柱体，垂直于弹簧轴线的横截面称为弹簧的断面)；然而，若弹簧质量必须考虑，其断面上内力变化规律可能会很复杂.柯红卫等研究了简谐振动的弹簧内力[10]，但在考虑弹簧质量情形下，纯简谐振动的实现很困难，比如通常所讨论的例子均匀拉伸后释放所建立的振动，并非简谐振动，而是多个本征振动叠加在一起的复合振动.可以推测此情形下，弹簧内力随时间和空间的变化规律应当不会很简单.但由于以前技术限制，大多教科书或学习辅导书往往止步于冗长的级数表达式.这样做，一则不直观，另则也不容易激发学生深入探究的兴趣.

本文将对弹簧质量必须考虑的振子的弹簧内力进行探究，并利用数学工具软件MATLAB的计算和图形功能把其复杂性展示出来，让学生对其复杂性有直观的认识，进而促进学习兴趣.

1 模型

在图1所示的模型中，设弹簧原长为l, 劲度系数k，弹簧的质量m′均匀分布(线密度ρl=m′/l)，质点的质量为m(为了方便讨论，后文经常使用质量比βm=m′/m这个参数).记位于弹簧原长x断面的位移为u(x,t).弹簧的波动方程为[1-4](也可参照弹性杆的纵向振动[11])

ut t=v2uxx

(1)

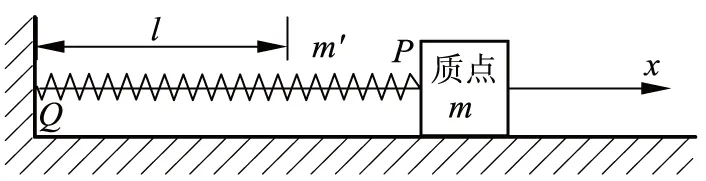
图1 模型

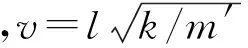
由边界条件(2)和(3)可导出第i阶无量纲本征频率μi方程[11]

βmcosμi-μisinμi=0

(4)

无量纲本征频率μi与有量纲的本征圆频率ωi之间的关系为

(5)

对应的本征函数如下

(6)

2 本征振动

2.1 内力

为了与文献[10]尽量一致，暂且假定振子发生了一阶本征振动(如果要发生这样的自由振动，必须精心控制弹簧各断面的初位移和初速度，使得二者与第一阶本征函数仅相差一个比例系数).

对这种特殊振动，弹簧各断面的位移为

(7)

其中,A和α分别为质点的振幅和振动初相位.注意质点m最大位移是Asinμ1，而不是A.

对质量不计的轻弹簧(m′=0)，弹簧内力沿轴线不变，且等于作用在弹簧两端的所谓“弹力”.但当质量不能忽略时，弹簧内力沿轴线变化规律正是本文要探究的问题.下面通过弹簧的局部变形来确定弹簧内力.

考虑未变形时位于x的断面.记该断面的局部伸缩率(在单位长度上的伸缩)为ux(ux=∂u/∂x)，相应的内力则能写成κux，其中κ是与弹簧劲度系数k有关的比例系数.为了确定κ与k的关系，假定弹簧退化成无质量情形，则弹簧总伸长量(此时发生均匀变形)为lux，由弹簧胡克定律得到的弹力为k×(lux)，它也等于从局部伸缩率角度的κux.这样得到κ=kl.利用这个关系，有质量弹簧各断面的内力可表示为(适合于任何形式的振动)

F(x,t)=klux

(8)

将式(7)代入式(8)有

(9)

2.2 表观劲度

通常说法“弹力与位移成正比”中：“位移”指的是质点m的位移，也就是图1中P点位移u(l,t)；力则是弹簧作用在质点上的力，它也等于式(9)取x=l(P点)的函数值.由式(7)和式(9)可知P端的弹力与该端点位移仍成正比，但是比例系数

(10)

不再恒等于弹簧的劲度系数k.文献[10]已指出这一点，但是文献[10]是基于动态时弹簧仍均匀变形的假定，所得到kB与式(10)有一定差异.

kB和k的关系与μ1有关，进而与质量比βm有关.

Q端的弹力和P端质点m位移比值为

(11)

它与文献[10]结果也有不同.

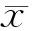
可化为

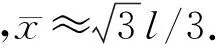
2.3 化解“佯谬”

因为动态下弹簧变形不均匀，其质心加速度üC(t)既非ü(l,t)/2，也非ü(l/2,t).正确的做法是对ü(x,t)进行积分平均得到质心加速度，即

也就是

(12)

弹簧所受合外力为

(13)

式(12)和式(13)表明弹簧运动没有违背质心运动定理.如果都能从第一原理出发并经严密数学演绎，就不会出现文献[12]的“佯谬”现象.

3 均匀拉伸模式

3.1 级数解

把弹簧准静态地均匀拉伸到一定长度之后释放，所形成的初条件为

对应这个初条件的振动并非简谐振动[2,13]，从文献[14]和[15]可以找到其级数解.这一问题在数学上完全等同于弹性杆一端带质点的自由振动问题[16,17].上述文献止步于位移的级数解，本文进一步探究弹簧内力特性.

采用本文的符号，各断面的位移函数表示如下：

(16)

其中系数

(17)

将式(16)代入式(8)有

(18)

式中系数

(19)

从式(18)和式(19)可以看出弹簧的内力与x关系复杂，远非“弹簧上各点张力变化呈线性变化”[18].

3.2 图形展示

先看两端Q和P处(见图1)的力，即

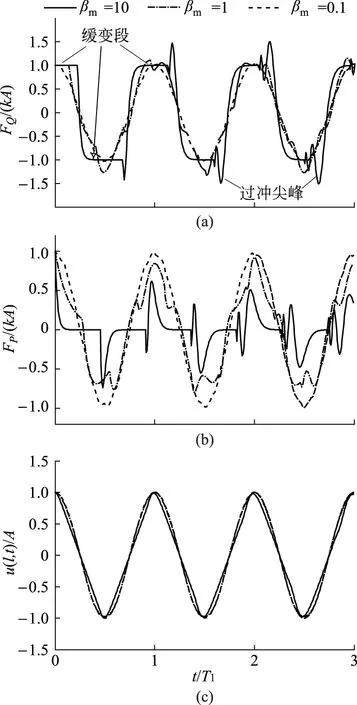
图2 释放初始阶段的力与位移

为了直观感受力的复杂性，使用MATLAB工具对式(20)和(21)进行了计算.两式均为级数和，我们只能取有限项来近似.数值实验表明，取10项即可.但为保险起见，图2中数据是取了前5000项之和.图2(a)和2(b)分别给出了刚释放不久左端FQ(t)和右端FP(t).质量比选择了βm=10(重弹簧),1和0.1(轻弹簧)3种情形.

振子的基频(第一阶频率)与βm有关.为了方便比较，图2中横坐标用振子基频所对应的周期T1作了无量纲化处理，这样使3条曲线按照基频的周期对齐.

图2(a)和2(b)直观地揭示了:βm越大，弹簧两端受力偏离简谐波越严重；随时间增长，不规则性也越明显.βm=10的曲线看不出有什么周期，而且有明显的过冲尖峰(弹簧左端面在过冲尖峰的瞬间受力可超过kA).在左端面,βm=10的曲线有明显的缓变段，这是因为处于右端的质点m释放之后，波动的作用需要一段时间后才能传到左端，在波动达到之前弹簧左端弹力保持不变.波动达到左端墙面后反射，再向右传.在没有传出之前，也同样存在缓变段.但是缓变段的时长因各阶本征振动不同步而变短.

总之,波传播总是需要时间的，因此只要弹簧有质量，弹簧左端力在一开始就有缓变期，只是βm越小，缓变期越短.

可以想象，随时间增长，力的不规则性肯定会增加.图3是1000T1～1003T1时段的变化曲线.除了时段外，图3条件与图2完全相同.图3的不规则性更加明显.如果βm比较小，变化曲线还是接近正弦波的，就如同文献[19]所报告的“位移、速度、加速度和力随时间的变化曲线,……,它们与理想的正弦曲线是接近的”，因为该文最大的βm为105.10/(11.98+80)=1.1426(当然实验测量电路一般都有低通滤波环节，它也会抑制高频波动).

为了体会介于Q和P之间内力的复杂性，图4用瀑布图的方式显示了沿轴线均匀分布的21个断面上内力随时间变化曲线(βm=10).图中x坐标对应断面的位置.图4(a)中最前面(x=0)一条粗线就是图2(a)中实线，而最后面(x=l)的粗线就是图2(b)中的实线.从该图可以体会内力的复杂性.在波动从P端向Q端传递过程中，图2(a)所标注的缓变段在Q点最长，而越靠近P点越短，这是因为波动来的越早.图4(b)与图3对应，可看出随时间增长，内力的不规则性非常明显.

3.3 定性解释

再回到图2.与力相比，图2(c)的质点位移曲线较为规则，尽管它也是无穷多个本征振动累加.数学上，图2和图3(c)通过数学式(8)与各自(a)和(b)联系起来.图3(c)图对整个弹簧变形的空间积分，而积分有平滑作用，即把频率高(对应高阶本征振动)的波动平滑掉，所以右端点的位移曲线较光滑.(a)和(b)两图反映内力，与局部伸缩率成正比.而局部伸缩率是位移对空间的微分，会突出频率高的成分.

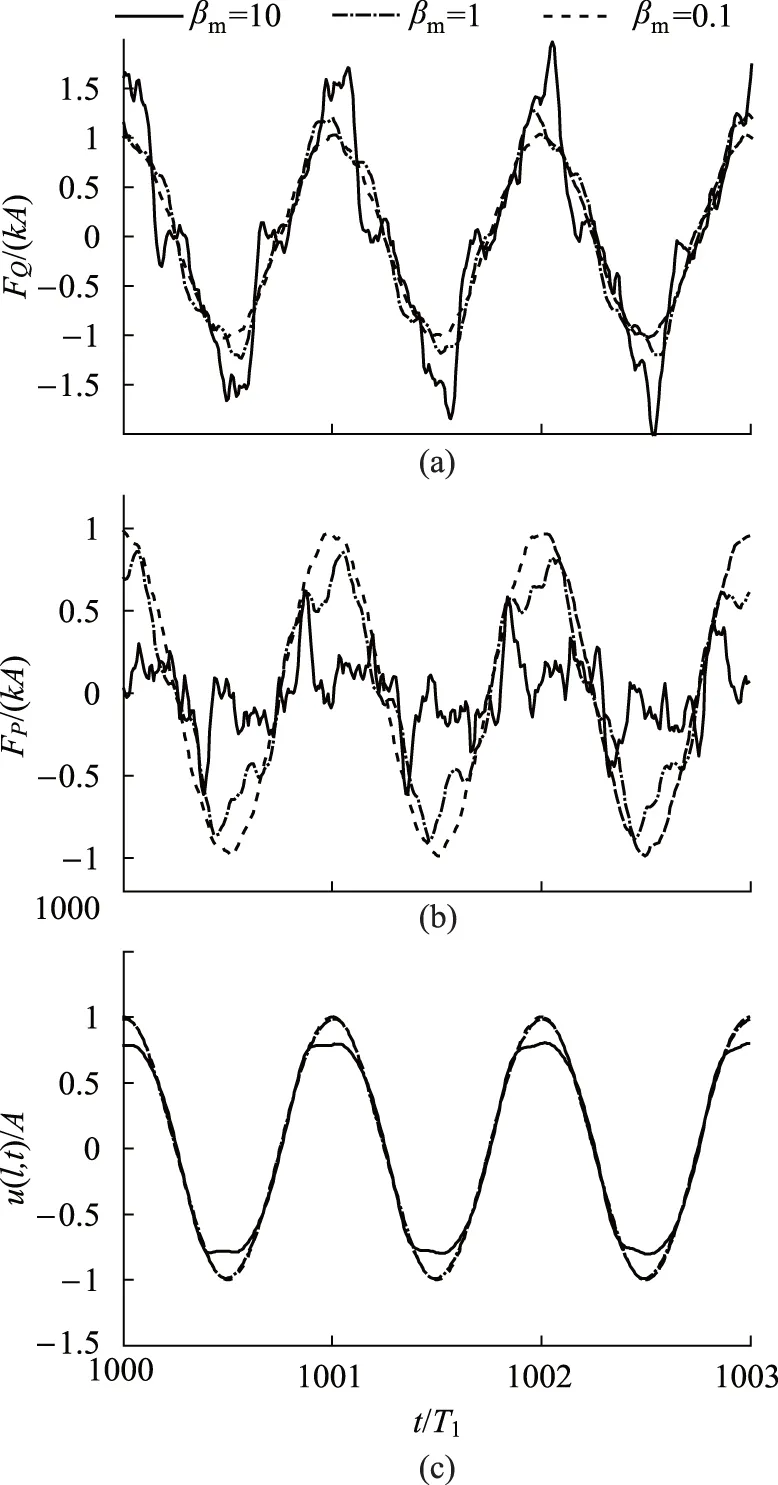
图3 释放长时间后的力与位移

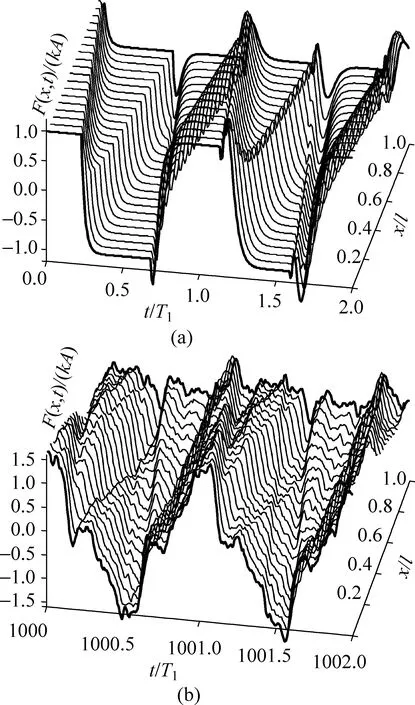
图4 内力复杂性

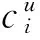
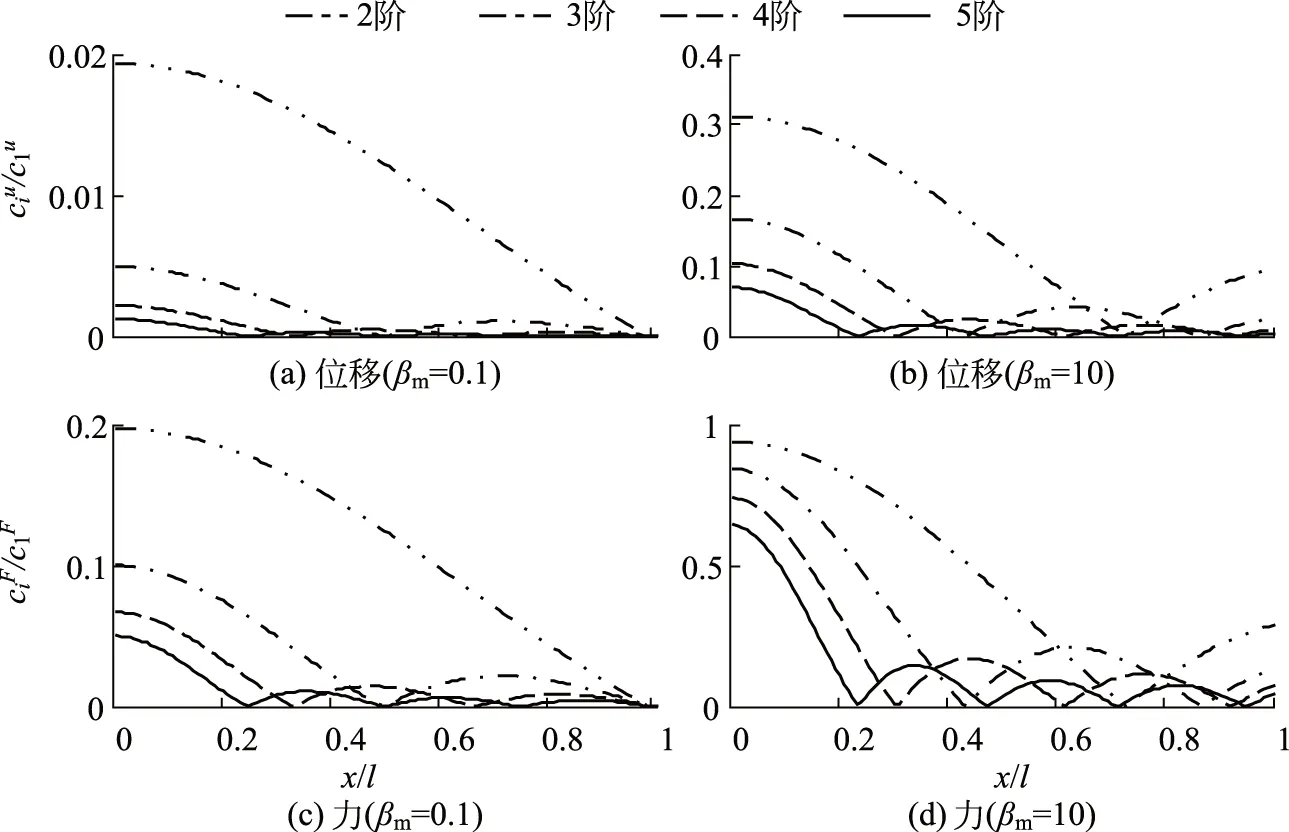
图5 非基频本征函数的贡献

为了对收敛速度有个直观体会，图5显示了位移和力的前2～5阶系数与基频系数比值.当质量比βm相对较小时(βm=0.1)，无论是力，还是位移，非基频的系数都比较小(图5(a)和图5(c)).图5(b)和图5(d)的βm比较大(βm=10，即质点质量只有弹簧质量的1/10)，此时位移第二阶系数可达基频的31%,力的第二阶系数可达基频的94%.显然，若βm比较大，就必须考虑高阶本征函数的贡献.

4 纯弹簧情形

4.1 位移

当质点m=0，振子只剩下弹簧了.此时βm=m′/m→∞.从式(4)可解出

μi=iπ/2

(22)

代入式(18)有

(23)

利用三角函数的积化和差公式，也可以将式(23)表示成方向相反的行波叠加

u(x,t)=R(x+vt)+R(x-vt)

(24)

其中

(25)

可以验证R(x)是周期为4l的三角波，如图6所示.

4.2 内力

弹簧内力为

F(x,t)=kl[R′(x+vt)+R′(x-vt)]

(26)

因为R(x)是分段函数，我们也必须对F(x,t)作分段处理.F(x,t)是以4l/v为周期的周期函数，故只需研究一个基本周期内的特性，因此时间限制为0≤t≤4l/v，而x的限制为0≤x≤l.在这两个限制下，x-vt应小于-4l而大于l.这个范围有两个分段点，即x-vt=-l,-3l，也就是t=(x+l)/v,(x+3l)/v.而对x+vt也有两个分段点，t=(l-x)/v和t=(3l-x)/v.再把周期边界的t=0和t=4l/v两个点加上，于是在基本周期内有6个关键点，它们把一个基本周期分成5段.相关信息汇总于表1.

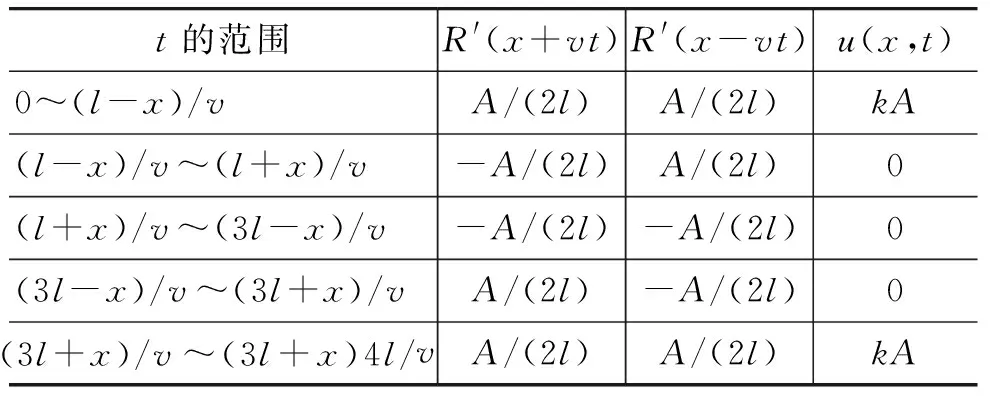
表1 弹簧内力

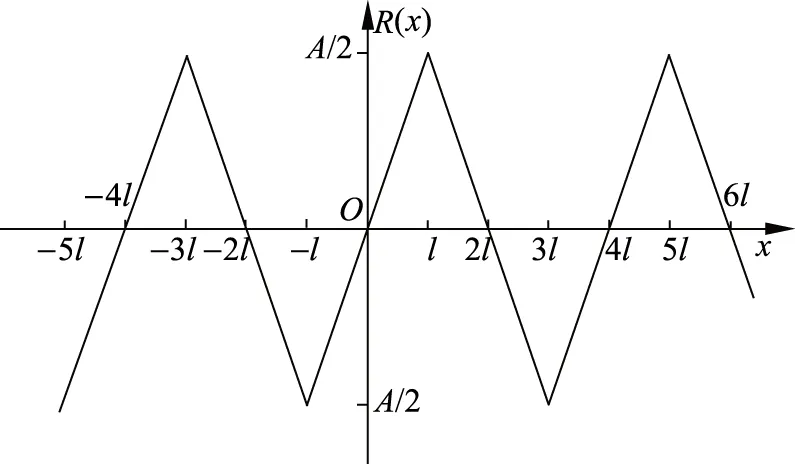
图6 行波波形

图7画出了x=0,l/4,l/2和3l/4共4个断面内力在一个基本周期内变化.x=0对应弹簧的左端，该处的内力不是拉，就是压，而在其他断面处弹簧存在不受力的状态，这是因为在该时段此断面无弹性波.此外各断面内力随时间变化呈不连续的方波.

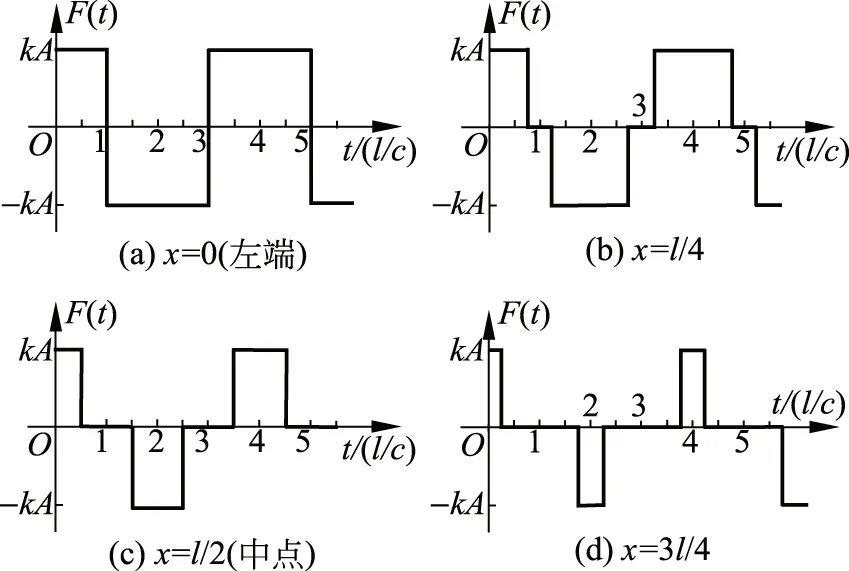
图7 质点质量为零情形的弹簧内力

4.3 验证牛顿第二定律

质心的加速度为

即

根据图6,R′(x)为偶函数，所以第二项和第四项都等于-R′(vt).第三项为R′(l-vt)=R′(vt-l).再根据图4可知R′(vt-l)=-R′(vt+l)，故而上式的第一项和第三项相抵消.最后有

üC(t)=-2v2l-1R′(vt)

与式(26)取x=0相比较，同样可知质心运动也没有违背牛顿定律(注意加速度正方向指向右，而按内力方向规则，弹簧左端的内力向左，从而上式右端有负号).

5 结语

弹簧质量振子是物理教学的经典模型.该模型相关知识的挖掘和积累，对丰富课堂教学、促进探究性学习仍具有现实意义.本文针对典型情形，就有质量振子的弹簧内力，进行了详细的探究.典型的情形包括本征振动，弹簧均匀拉伸-释放所建立的振动等.

研究发现振子的内力与相关文献所声称的有差异，而弹簧均匀拉伸-释放所建立的自由振动也不是简谐振动，尤其是内力偏离简谐更明显.弹簧质量越大，内力偏离简谐波越严重.用MATLAB工具以图形展示了这种不规则性.当质点质量零时，内力变成时间的周期性方波函数.

[1] 丁履成,司明扬.有质量的弹簧的振动问题[J].大学物理,1985,4(9):15-18.

[2] 刘大鹏,关荣华.弹簧质量对弹簧谐振子圆频率的影响[J].大学物理,1995,14(10):22-24.

[3] 于凤军,王春明.弹簧系统振动周期的近似公式[J].大学物理,2012,31(3):13-15.

[4] 沈钟伟,张峰.弹簧质量对振动周期的影响[J].大学物理,2013,32 (3):44-45.

[5] 王锋, 唐国金.考虑弹簧质量的振子精确解[J].物理与工程,2003,13(2):28-30.

[6] 何连超.有质量弹簧的振动周期探讨[J].物理与工程,2011,21(5):1-2.

[7] 任保文.弹簧的振动[J].物理与工程,2014,24(1):19-21.

[8] 陈奎孚,贾贵儒,黄峰.对有质量弹簧的振子基频作近似的若干算法之比较[J].大学物理,2014,33(8):18-20.

[9] 朱洪玉.关于质点弹簧系统在重力作用下的静平衡与振动[J].大学物理,2009,28(1):1-10.

[10] 柯红卫,刘坦,赵耀.有质量弹簧的振动与弹性力[J].大学物理,2013,32(5):17-18.

[11] 陈奎孚.机械振动基础[M].北京:中国农业大学出版社,2011:312-318.

[12] 田蓬勃,赵强.弹簧振子佯谬[J].物理与工程,2002,12(1):12-13.

[13] 黄兆梁.对有质量弹簧的振子系统振动周期的探讨[J].大学物理,2011, 30(5):32-34.

[14] 徐世良.数学物理方法解题分析[M].南京:江苏科学技术出版社,1983:519-527.

[15] 陈奎孚,付志一,高阳.弹簧质量不能忽略的振系之自由振动[C].北京力学会.第20届学术年会论文集, 北京,2014：640-644.

[16] 林琼桂.与质点连结的弹性杆的振动[J].大学物理,2004,23(3):18-20.

[17] 徐建军,胡嗣柱.用Laplace变换法求解端点系有集中质量的弹性杆的振动问题[J].大学物理,2004,23(12):12-17.

[18] 于秀安.计算有质量弹簧的形变量[J].技术物理教学,2013,21(2):85-86.

[19] 褚幼令,陈乃东,王挚平.弹簧振子振动特性的计算机实时测量[J].大学物理,1998,17(5):32-34.

■

THE SPRING’S INTERNAL FORCE OF THE VIBRATOR WITH A MASSIVE SPRING

Chen Kuifu1Huang Feng1Jiang Xiao2Zhao Jianzhu3

(1College of Science, China Agricultural University, Beijing 100083;2Schools of Mechanical & Electrical Engineering, Beijng Vocational College of Agriculture, Beijing 102208;3College of Engineering, China Agricultural University, Beijing, 100083)

The spring’s internal force of a vibrator with a light spring is trivially a constant, while the case with a massive spring is much sophisticated. This problem was investigated in detail, and was visualized by the mathematical tool Matlab. This study shows, firstly, that the spring’s internal force varies along the spring’s length for a massive spring case. Secondly, the vibration established by uniformly stretching and releasing the spring is not a simple harmonic motion; as a result, the spring’s internal force deviates from the simple harmonic pattern. Thirdly, the deviation is more and more significant as the spring mass increases. Finally, the internal force lends itself to be a square wave when the lumped mass is null.

mass-spring vibrator; wave motion; partial differential equations; internal force

2015-06-03；

2016-02-28

2015年度北京高等学校教育教学改革立项项目(编号：2015-ms049;名称：以工程教育认证为导向的车辆工程专业实践教学改革研究与实践).

陈奎孚,男，教授.从事力学和振动的教学与研究.chenkuifu@cau.edu.cn

赵建柱，男，副教授.主要研究方向为车辆动力学.zhjzh@cau.edu.cn

陈奎孚,黄峰,蒋晓,等. 有质量弹簧振子的弹簧内力[J]. 物理与工程，2016，26(5)：6-11，15.