某型充气式再入减速热防护结构优化分析

黄明星 王伟志

（北京空间机电研究所，北京 100094）

某型充气式再入减速热防护结构优化分析

黄明星 王伟志

（北京空间机电研究所，北京 100094）

随着航天技术的不断发展，充气式再入返回技术逐步成为国际上的研究热点。文章以充气式再入返回系统为背景，对柔性热防护结构进行了优化分析。首先，参考美国充气式再入返回试验中典型的充气式再入返回系统热防护材料和结构设计，建立了柔性热防护结构的一维传热模型。然后，根据差分算法，推导出了柔性热防护结构各功能层传热控制方程的离散格式。文章以材料的耐热能力为约束条件，柔性热防护结构各功能层的材料和铺层这两个参数为优化变量，得到了给定热边界条件下柔性热防护结构的优化方案。最后，通过差分算法计算出柔性热防护结构各功能层再入过程中的温度响应，并用ANSYS有限元方法对结果进行了验证。计算结果表明各功能层的材料分别为Nextel720、Refrasil 2000、Upilex，对应的铺层数分别为 1、3、1时，为最优的柔性热防护结构设计方案，此时柔性热防护结构的面密度为2.128kg/m2。

充气再入 气动热 优化设计 热防护 航天返回

0 引言

随着充气式再入返回技术越来越受到人们的重视，其关键的柔性热防护结构也日益成为人们研究的热点。充气式再入返回的热防护系统（thermal protection system，TPS）采用了结构和热防护的一体化设计，其热防护结构不仅要承受热载荷，而且还要承受再入、减速过程的气动载荷，因此必须考虑材料的高温变形和温度对材料性能的影响，另外高温下材料的气体渗漏性也必须极低。此外，为了保证其气动性能，充气式再入返回系统柔性热防护结构充气后也不能有较大的形变[1-3]。

充气式再入返回系统柔性热防护结构由防热层、绝热层、气密层组成。防热层位于TPS的最外面，承受最高的温度和剪切应力，主要用来阻隔热流。防热层多使用高强轻质的柔性编织材料，如氧化铝纤维（Nextel）、碳纤维等。中间的绝热层承受的温度较防热层低，主要用来防止热流向TPS内部传递，多使用碳纤维隔热毡布、无定形二氧化硅隔热毡布等。气密层用来防止气体渗漏，保持充气结构的形状，多使用聚酰业胺（Kapton）薄膜[4]。图1为充气式再入返回试验（inflatable reentry vehicle experiment，IRVE）系列典型充气再入系统，其中是红色部分为柔性热防护结构。图2为IRVE的一种基准柔性热防护结构[5]。

图1 IRVE系统Fig.1 System of IRVE

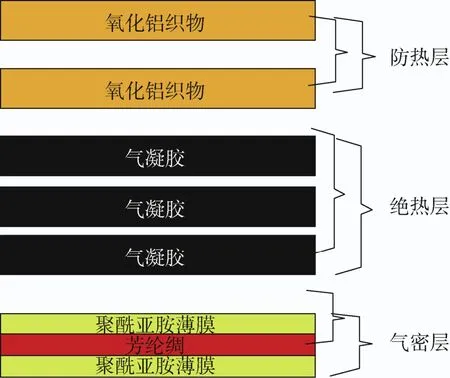
图2 柔性热防护结构Fig.2 Flexible thermal protection structure

国内充气式再入返回系统柔性热防护结构还处于理论研究阶段，国外大多是通过风洞试验及飞行试验来研究不同材料、结构的柔性热防护结构的热学性能及力学性能[5-6]。

本文以充气式再入返回系统柔性热防护结构为研究对象，建立了柔性热防护结构的一维传热模型，然后采用差分算法对柔性热防护结构功能层铺层及材料分别进行优化分析，得到满足防热要求且质量最小的设计方案。最后通过差分算法及ANSYS软件仿真对最优设计方案再入过程各功能层的温度响应进行估算，并用ANSYS仿真结果对差分算法进行了验证。

1 模型描述与求解

本文的研究对象为采用钝—锥外型的充气式再入系统如图 3所示，外形参数参考 IRVE的设计先例[7-8]，刚性球头半径r=0.3m。锥体部分采用可充气展开的柔性热防护结构，半锥角为60°，展开的底部半径为 2.05m。考虑到充气式再入系统从空间站返回的情况，再入高度可取110km，再入速度取第一宇宙速度7.8km/s，再入角为–2°。

1.1 柔性热防护结构传热模型

充气式再入返回系统再入过程中热环境不断变化，所以对柔性热防护结构各功能层温度响应的求解可以看作非稳态温度场的导热问题[7]。文献[8]中Patran Thermal和Thermal Desktop等软件仿真结果表明只考虑一维传热精度就足以满足计算要求。因为文中采用差分形式对传热控制方程进行离散，所以建立柔性热防护结构一维传热的差分传热模型。

柔性热防护结构由防热层、绝热层、气密层 3个功能层组成，每一功能层都由很多铺层紧密结合而成，其由外向内的厚度方向设为x，只考虑沿着厚度方向的一维传热，如图4所示。把柔性热防护结构各功能层离散成单元，防热层、绝热层、气密层的内部离散单元厚度分别为ΔxF、ΔxJ、ΔxQ，下标F、J、Q分别表示防热层、绝热层、气密层。为了更加准确的确定表面单元的温度，表面单元厚度为内部单元的一半。图中T表示温度，下标u、v、w则表示相应功能层最后一个离散单元编号。每个功能层的单元数可以根据求解方程稳定性要求而相应增加。T∞、H分别是气密层内侧空气温度和对流传热系数。

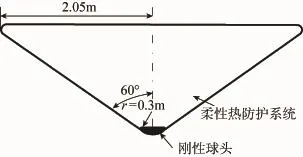
图3 展开的充气式再入返回系统Fig. 3 Deployed inflatable reentry vehicle

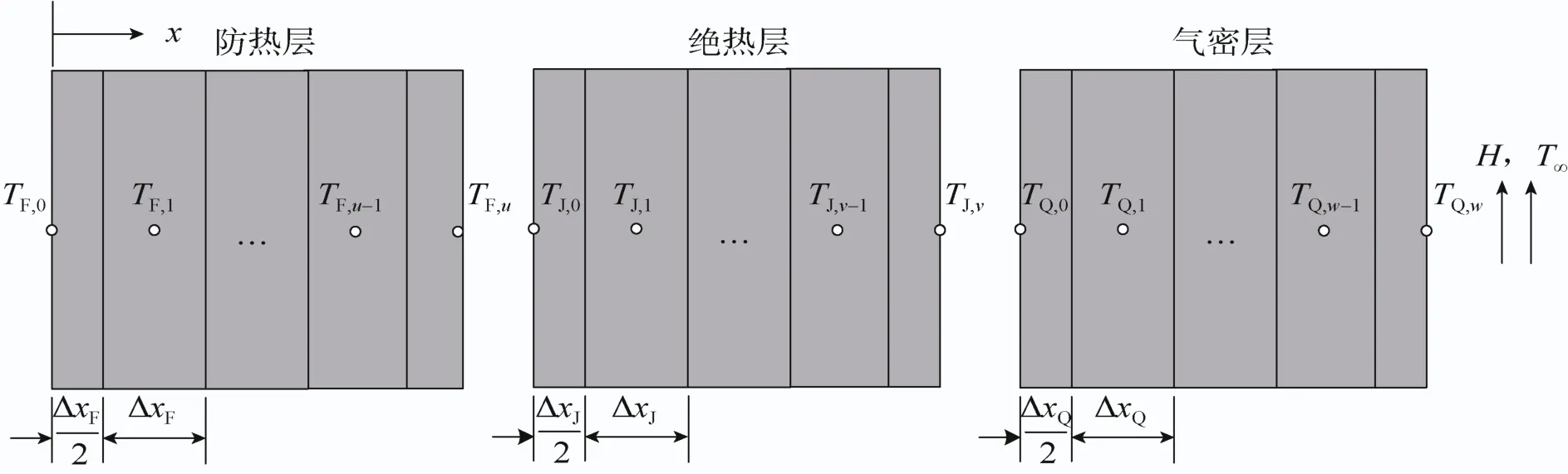
图4 柔性热防护结构一维传热模型Fig. 4 One dimensional thermal model of flexible thermal protection structure

由于柔性热防护结构各功能层内部铺层是紧密粘连在一起，故在分析其传热时有如下假设[6]：

1）只考虑固体之间的热传导，不考虑辐射和对流；

2）各功能层的接触面的接触热阻相同且不随着温度变化，不考虑功能内部的接触热阻。

1.2 材料参数与控制方程

根据能量守恒原理和傅里叶定律建立不稳定温度场差分方程。将柔性热防护结构划分单元，各接触面温度如上图4所示。单元的控制方程为[9]：

式中 ρ、c、λ分别是材料的密度、比热容和导热系数；t为时间。

使用古典显式差分格式，时间方向取向前差分，空间方向的二阶导数取中心差分[10-11]，对单元的控制方程进行离散有：

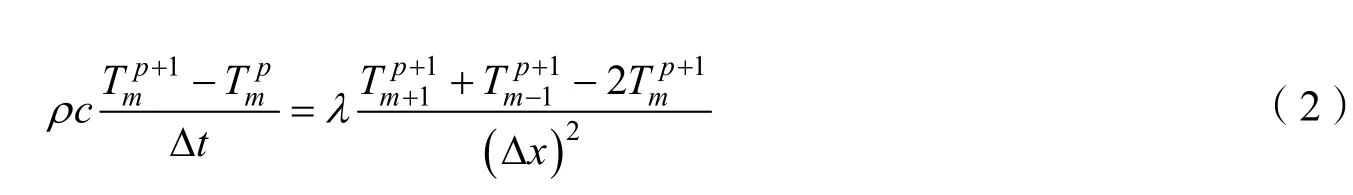
式中 Δt为时间间隔；Δx为各功能层离散单元的厚度；下标m表示内部离散单元编号；上标p表示时间离散点。

对于防热层中间单元，由有限差分分析可以得到其显式离散格式：

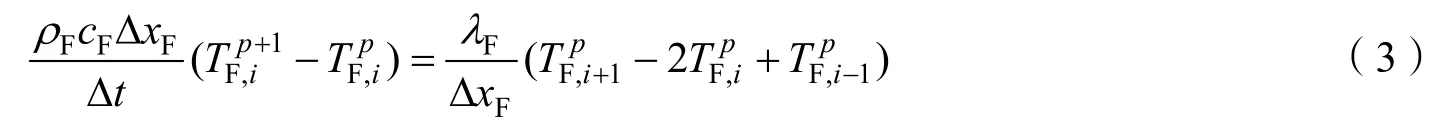
式中 下标i为功能层中铺层编号。

对于绝热层中间单元有：

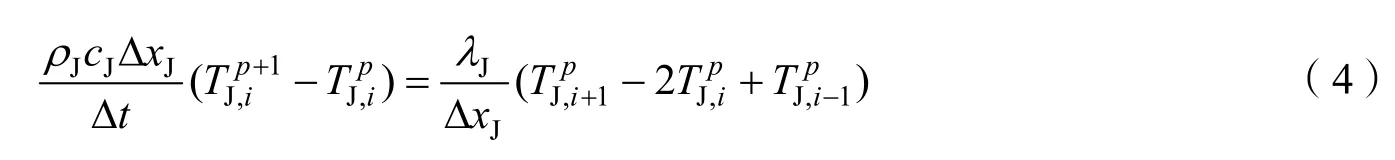
对于气密层中间单元有：

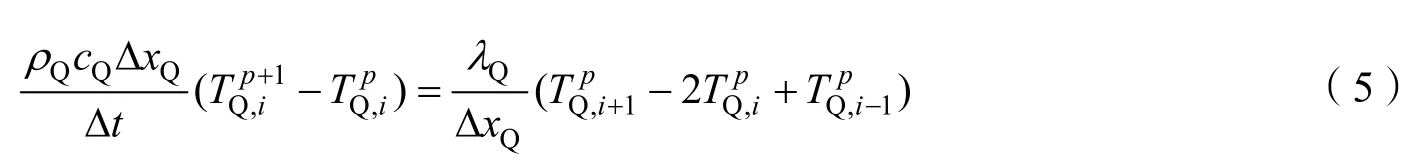
如果考虑各功能层之间的接触热阻，那么各功能层的接触面温度将不再相等，假设防热层与绝热层的接触热阻为R1，绝热层与气密层的接触热阻为R2，对于接触处单元，其离散形式分别为：

1）对于防热层与绝热层接触单元有：

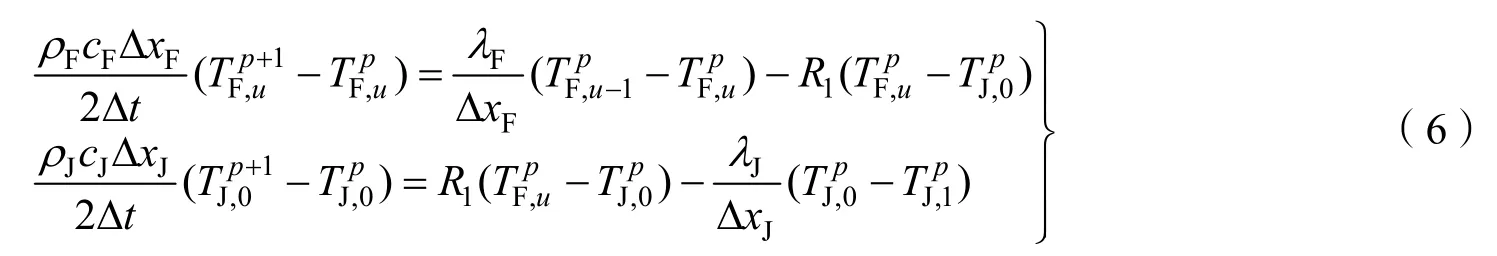
2）对于绝热层与气密层接触单元有：

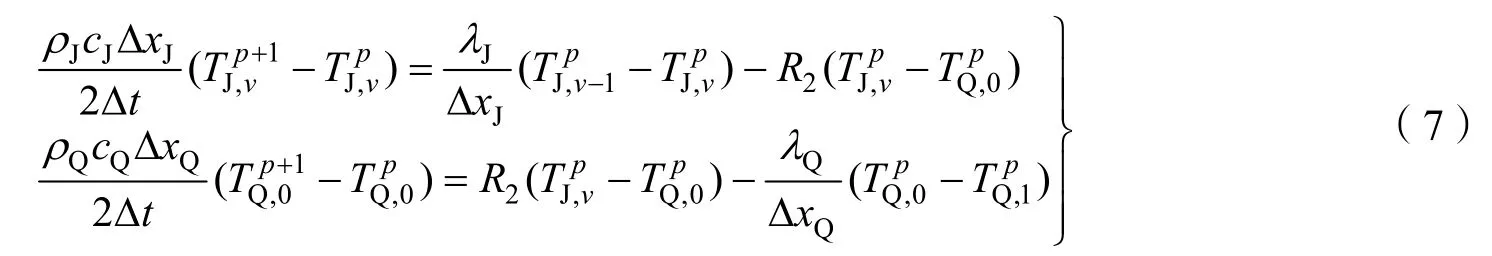
对于气密层的右边界条件有：

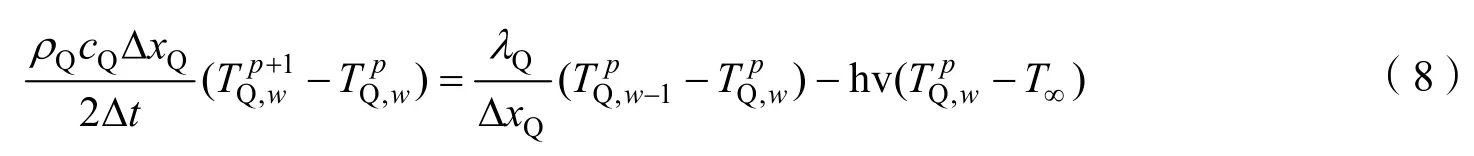
数值差分算法求解初值和边值问题，每步计算总会产生舍入误差，为了保证有限差分格式计算结构稳定，必须使所求温度单元前一时刻有关的系数不能小于零，必须满足[11]

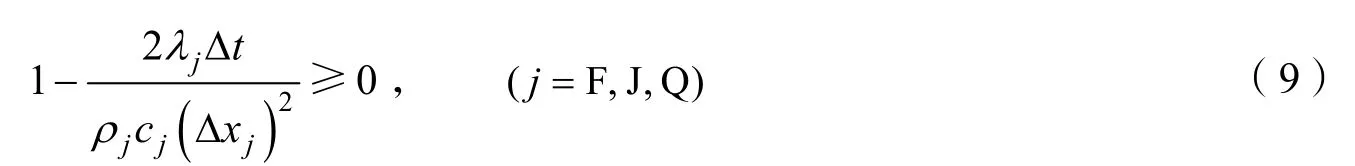
因此在用古典显式差分格式进行数值计算时，必须根据结果的稳定与否来实时调整求解的时间步长及空间步长，从而确保求出正确的柔性热防护结构各功能层的再入温度响应。

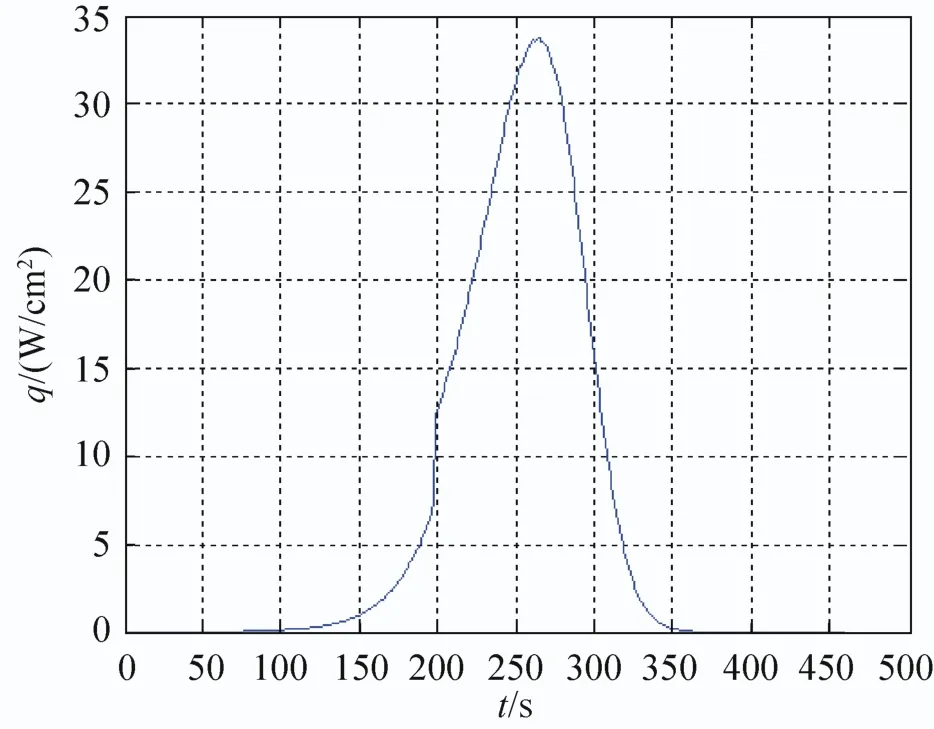
图5 柔性热防护结构外热流变化曲线Fig.5 External heat flux of flexible thermal protection structure

1.3 边界条件与初始条件

柔性热防护结构的防热层外边界为壁面边界条件，其再入过程的热流变化可以根据工程算法计算给出，如图5所示，图中q为热流密度，其最大值约为34W/cm2。再由柔性热防护结构表面能量守恒关系得到其温度变化，以此作为差分计算时柔性热防护结构防热层外表面的温度。在t=200s处是自由分子流与过渡流的分界点，因为热流计算桥函数的原因，此处出现了奇点。

柔性热防护结构气密层内侧并不是完全绝热，故采用对流边界条件，对流系数可根据对流环境[12]初步取为40W/(m2·K)。柔性热防护结构各功能层在再入过程开始时的初始温度都取为293K。

2 柔性热防护结构的优化设计

充气式再入返回系统返回过程中，其柔性热防护结构的表面温度可以达到1 000K以上，因此必须有足够的厚度以达到防热目的，但是另一方面，为了方便折叠包装，降低成本，又要求柔性热防护结构的厚度和质量越小越好。下面对柔性热防护结构进行防热与质量的一体化优化。

2.1 约束条件和优化目标、方法

充气式再入返回系统柔性热防护结构的防热层、绝热层、气密层厚度分别为hF、hJ、hQ，各功能层每种材料的铺层厚度分别为hF0、hJ0、hQ0，铺层厚度一般与材料的品牌/型号相关，且为定值。各功能层的铺层层数分别为kF、kJ、kQ则有：

各功能层材料最高使用温度分别为TFlim、TJlim、TQlim，每一种材料选择方案中防热层、绝热层、气密层的最高温度分别为TFmax、TJmax、TQmax。为了求出满足要求的且质量最小的柔性热防护结构，列出优化的约束条件及目标函数[13]。

约束条件为：

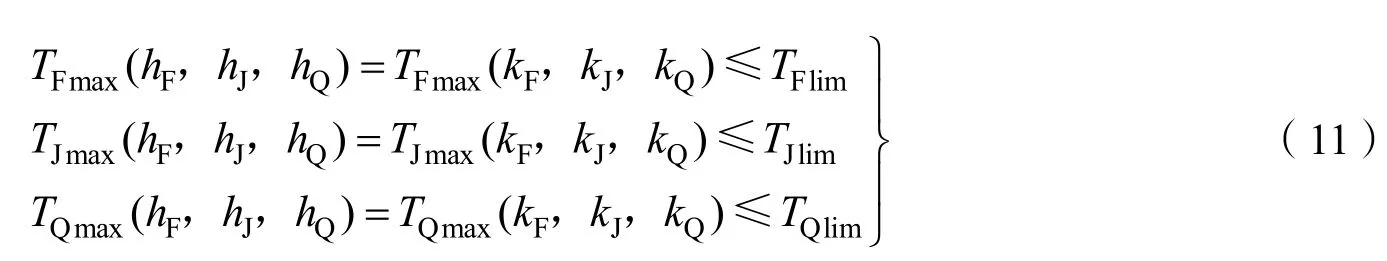
为了使柔性热防护结构的质量尽可能的小，选取柔性热防护结构面密度为目标函数：

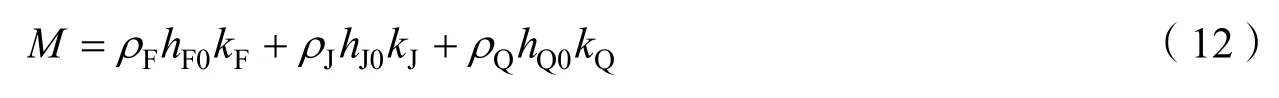
式中 M为柔性热防护结构的面密度。

优化过程分为材料优化及厚度优化两个方面。首先从备选的材料中选出可能满足方案的防热层、绝热层和气密层材料，对于每一种材料组成方案可求出分别满足三个约束条件的 kF、kJ、kQ，每个约束方程求出的kF、kJ、kQ都在三维空间构成一个可行区域，然后把这三个可行区域进行叠加，得到的可行区域就是能满足三个约束条件的铺层数。在这个区域内找出目标函数最小值，最后通过比较不同的材料方案的最小目标函数，从而求出面密度最小的柔性热防护结构设计方案。

2.2 差分算法对热防护层的优化

为了求出目标函数的最小值，在常用的柔性热防护材料[7,14]中选取了可能满足各层最大使用温度的功能层材料。其中防热层材料选择氧化铝纤维织布Nextel 720，因为防热层材料中氧化铝纤维织布Nextel 720与Nextel 440的热学参数基本相同，但前者密度更小[15]。绝热层选取三种材料，气密层选取两种材料，材料选择如表1，柔性热防护结构典型材料的热学参数可以参考文献[8]中的数据。

假设每个功能层只选一种材料，表中可组合出6种可能的材料选择方案。每一种材料选择方案，其每个功能层的铺层数都可以变化，参考充气式再入返回系统相关的文献[16-17]，其热防护结构每个功能层的铺层数一般不超过10，所以在优化过程中设置每功能层的最大铺层数为10层，故每一种材料选择方案都有1 000种铺层设计。采用差分算法编程对6种材料选择方案分别优化求解，求出满足使用温度条件的最小热防护层面密度。图6是进行柔性热防护结构优化设计的编程流程图。

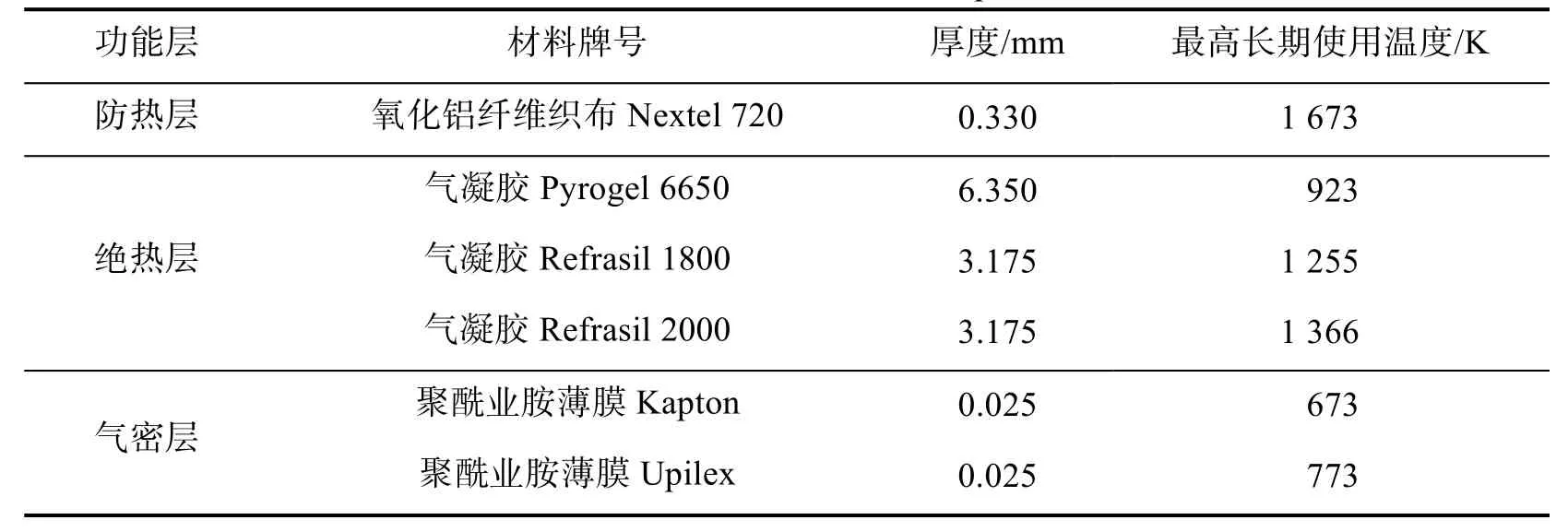
表1 柔性热防护结构材料的选择方案Tab.1 Material selection of flexible thermal protection structure

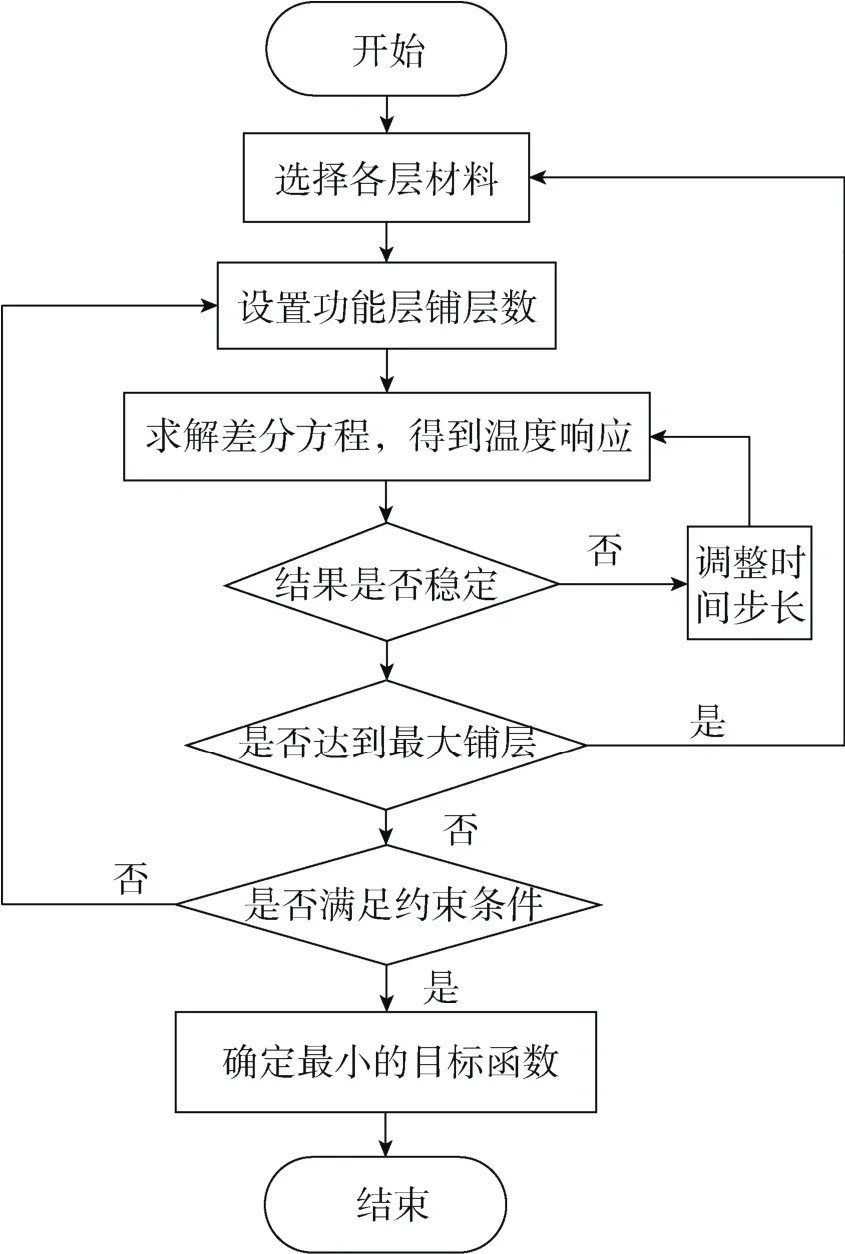
图6 优化流程图Fig.6 Optimization flow

以下对 6种材料选择方案其中一种的优化过程进行详细介绍。当各功能层材料选为：Nextel 720、Refrasil 2000、Kapton时，该材料选择方案1 000种铺层设计优化结果如下：图7～9分别是柔性热防护结构在不同铺层数下TFmax、TJmax、 TQmax分布的四维描述。图中沿着绝热层铺层数方向设置了 10个切片图，每个切片图表示相同绝热层材料铺层数，及不同防热层、气密层铺层数设计方案的温度分布。

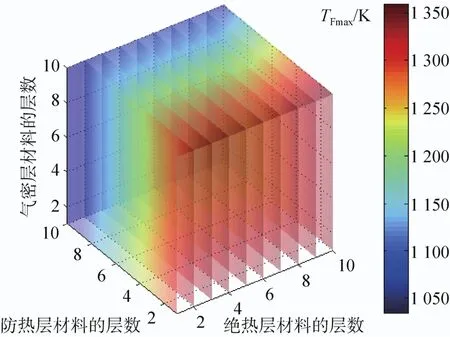
图7 各铺层数下的绝热层外表面温度响应Fig.7 Upper surface temperature response of outer fabric

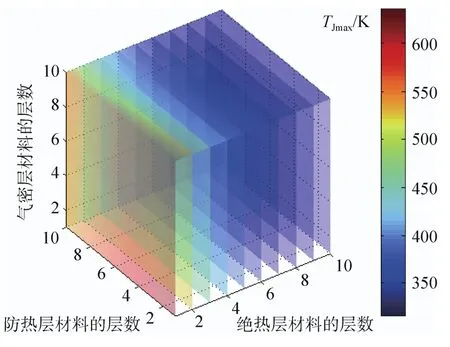
图8 各铺层数下的气密层外表面温度响应Fig.8 Upper surface temperature response of insulator

从图中可以看出TFmax、TJmax、TQmax的最小值均小于相应功能层材料的最高使用温度，所以一定有铺层数使得温度满足约束条件。在数值求解的过程中已经把不满足最大使用温度条件的设计方案去除，故图9中空白表明其部分铺层数不能满足气密层材料的温度约束条件。

把图7～9中分别满足3个温度约束条件的铺层数叠加在一起，其交集就是满足所有温度约束条件的铺层数。

在这些铺层数区域上绘制热防护结构质量分布的四维图，见图10。图中各功能层铺层数方案的颜色对应该方案的柔性热防护结构的面密度，红色表示面密度大，蓝色表示面密度小。图中结果表明，该材料选择方案的最优铺层设计为：防热层、绝热层、气密层的铺层数分别为 1、3、1。此时柔性热防护结构的面密度最小，最小值为2.131kg/m2。

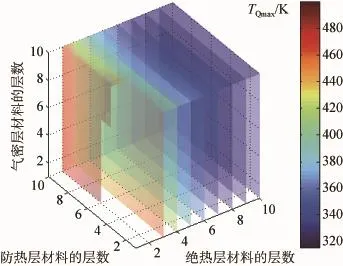
图9 各铺层数下的气密层内表面温度响应Fig.9 Lower surface temperature response of gas barrier

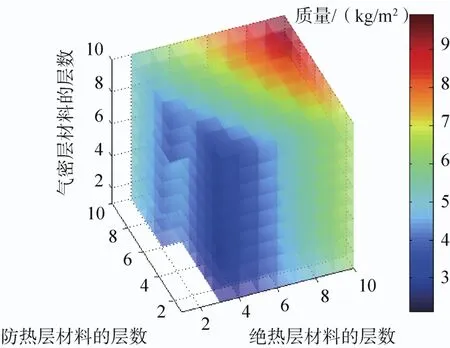
图10 各铺层数下柔性热防护结构的质量分布Fig.10 Mass distribution of various number of layers

同理，可以求出其它5种材料选择方案的最优铺层设计。最后的计算表明：Refrasil 6650的最高使用温度较低，当绝热层材料选择Refrasil 6650时无论如何都不能同时满足3个约束条件。满足约束条件的 4种料选择方案最优铺层设计总结见表 2，其中再入最高温度是指该热防护功能层再入过程中达到的最大温度。从表中可以看出各方案最优铺层设计中功能层的再入最高温度都接近其材料的最高使用温度。

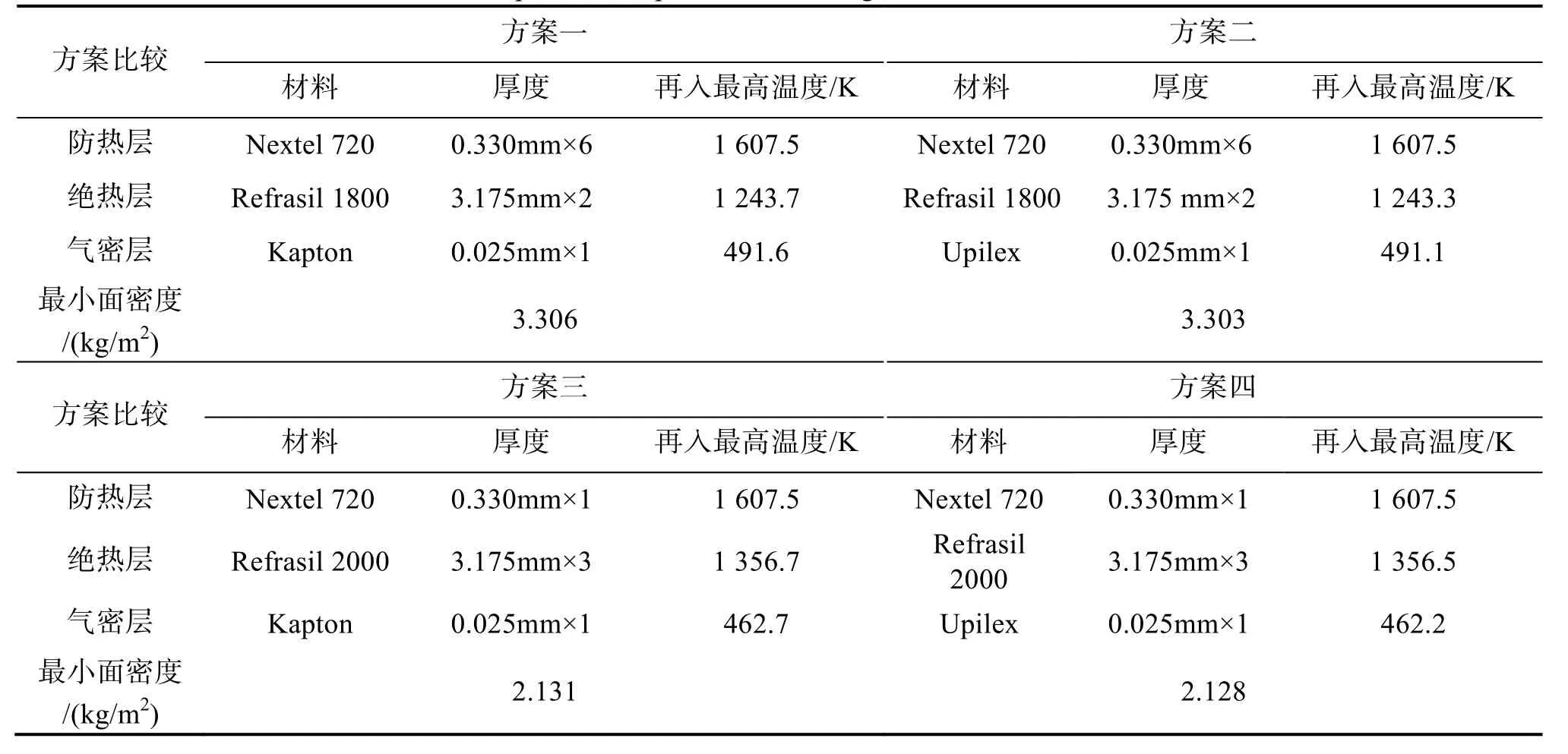
表2 各材料选择方案优化解的对比Tab.2 Comparison of optimization among various material selections

上表中列出了柔性热防护结构各材料选择方案的最优铺层设计，下面通过比较这些材料选择方案的最优铺层设计，来进行柔性热防护结构的材料优化。由于Kapton和Upilex材料热学参数基本相同，所以表中方案一与方案二、方案三与方案四的温度分布基本相同，但是Upilex密度更小，所以气密层材料选择Upilex。

从表中可以看出，柔性热防护结构的最优材料设计为方案四。此时不仅可以满足所有的温度约束条件，而且得到最小的目标函数值，最优柔性热防护结构的最小面密度为 2.128kg/m2，而文献[8]中 IRVE的柔性热防护结构其面密度约为2.62kg/m2。

2.3 最优设计的温度响应及ANSYS验证

对于上文经过铺层及材料优化得到的最优柔性热防护结构，即防热层采用1层Nextel 720，绝热层采用3层Refrasil 2000，气密层采用1层Upilex，分别用差分算法及ANSYS瞬态传热模块进行仿真计算。

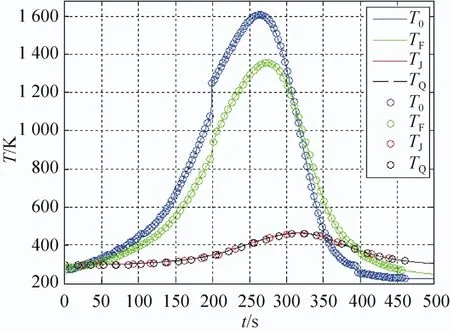
图11 ANSYS与差分算法结果对比Fig.11 Comparison between ANSYS and difference algorithm results

图11是差分计算与ANSYS仿真的结果，图中圆圈表示ANSYS仿真结果，曲线表示差分算法结果。T0表示柔性热防护结构再入过程中防热层外表面的温度变化，由边界条件给出，即图中蓝色部分，其最高温度为1 607.5K。绿色表示绝热层外表面再入过程的瞬态温度响应，其变化规律与外界作用温度一致，再入过程最高温度为1 356.5K，小于防热层材料Refrasil 2000的最高使用温度。红色、黑色分别表示气密层外、内表面再入过程的瞬态温度响应。因为气密层的厚度很小，其外、内表面的温度相差不大，而且经过绝热层之后，气密层再入过程的温度比较小，最高温度在462.2K左右。

对比差分算法与ANSYS仿真得到的柔性热防护结构各功能层的温度变化，可以看出这两种方向得到的结果基本重合，这也验证了文中编写的差分算法的正确性。

3 结束语

本文以某型充气式再入返回系统为背景，通过估算再入过程中热流环境，对柔性热防护结构进行防热与质量的一体化优化设计，并对最优设计方案再入过程的温度响应进行了仿真计算：

1）建立了考虑一维传热的柔性热防护结构的差分传热模型，求取了柔性热防护结构各功能层传热的差分方程；

2）对柔性热防护结构6种材料选择方案的功能层铺层进行了优化，得到了各个材料选择方案的最优铺层设计，然后比较各材料选择方案的最优铺层设计，经过材料及铺层双层优化后得到了最优柔性热防护结构设计，此时各功能层的材料分别为Nextel 720、Refrasil 2000、Upilex，对应的铺层数分别为1、3、1，柔性热防护结构的面密度为2.128kg/m2；

3）分别用差分算法及ANSYS软件对最优的柔性热防护结构的温度响应进行了仿真，结果不仅验证了最优柔性热防护结构的防热性能，而且还证明了文中差分算法的正确性。

本文的研究为柔性热防护结构的防热与质量一体化优化提供了一种有效工具，优化结果可以为相关设计分析提供参考。

References)

[1]曹旭. Al2O3纤维在空间充气式气动阻尼结构中的应用[J]. 航天返回与遥感, 2010, 31(5): 16-21. CAO Xu. The Application of Al2O3Fibers in Space Inflatable Aerodynamic Decelerator Structures[J]. Spacecraft Recovery & Remote sensing, 2010, 31(5): 16-21. (in Chinese)

[2]夏刚, 秦子增, 张晓今. 充气防热罩技术发展现状[J]. 导弹与航天运载技术, 2002, (1): 19-24. XIA Gang, QIN Zizeng, ZHANG Xiaojin. Development Status of Inflatable Thermal Shield Technology[J]. Missiles and Space Vehicles, 2002(1): 19-24. (in Chinese)

[3]王伟志. 充气展开式新型空间回收技术展望[J]. 航天返回与遥感, 2004, 25(1): 1-5. WANG Weizhi. Forecast of the New Type Inflatable Deployment Space Recovery Technology[J]. Spacecraft Recovery & Remote Sensing, 2004, 25(1): 1-5. (in Chinese)

[4] LINDELL M C, HUGHES S J, DIXON M, et al. Structural Analysis and Testing of the Inflatable Re-entry Vehicle Experiment (IRVE)[J]. AIAA Paper, No.1699: 1-4, 2006.

[5] DEL CORSO J A, CHEATWOOD F M, BRUCE W E, et al. Advanced High-temperature Flexible TPS for Inflatable Aerodynamic Decelerators[C]. 21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Dublin, Ireland, 2011, 1: 139-161.

[6] DEL CORSO J A, BRUCE W E, LILES K A, et al. Thermal Analysis and Testing of Candidate Materials for PAIDAE Inflatable Aeroshell[C]. 20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Seattle, Washington, 2009.

[7] LICHODZIEJEWSKI L, KELLEY C, TUTT B, et al. Design and Testing of the Inflatable Aereshell for the IRVE-3 Flight Experiment[C]. 53rd AIAA/ASME/ASCE/AHS/ASC Structures. Structural Dynamics and Materials Conference. Honol-ulu, Hawaii, 2012．

[8] MOSS J N. Low-density Aerodynamics for the Inflatable Re-entry Vehicle Experiment[A]. AIAA Paper, No.1189, 2006.

[9]曹玉璋. 传热学[M]. 北京: 北京航空航天大学出版社, 2001: 152-159. CAO Yuzhang. Heat Transfer[M]. Beijing: Beihang University Press, 2001: 152-159. (in Chinese)

[10]孔祥谦. 有限单元法在传热学巾的应用[M]. 北京: 科学出版社, 1998: 139-145. KONG Xianqian. The Application of the Finite Element Method in Heat Transfer[M]. Beijing: Science Press, 1998: 139-145. (in Chinese)

[11]颜庆津. 数值分析[M]. 北京: 北京航空航天大学出版社, 2012: 252-258. YAN Qingjin. Numerical Analysis[M]. Beijing: Beihang University Press, 2012: 252-258. (in Chinese)

[12]葛新石, 叶宏. 传热和传质基本原理[M]. 北京: 化学工业出版社, 2007: 6. GE Xinshi, YE Hong. Fundamentals of Heat and Mass Transfer[M]. Beijing: Chemical Industry Press, 2007: 6. (in Chinese)

[13]陈立明, 戴政, 谷宇. 轻质多层热防护结构的一体化优化设计研究[J]. 力学学报. 2010, 43(2): 289-294. CHEN Liming, DAI Zhen, GU Yu, Integrated Optimization Design of Light-weight Multilayer Thermal Protection Structures[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 43(2): 289-294. (in Chinese)

[14]DELCORSO J A, BRUCE W E, HUGHES S J, et al. Flexible Thermal Protection System Development for Hypersonic Inflatable Aerodynamic Decelerators[C]. International Planetary Probe Workshop. Toulouse France, 2012: 9, 18-22.

[15]HUGHES S J, WARE J S, DELCORSO J A, et al. Deployable Aeroshell Flexible Thermal Protection System Testing[C]. AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Seattle, Washington, AIAA-2009-2926, 2009.

[16]HUGHES S J, DILLMAN R A, STARR B R, et al. Inflatable Re-entry Vehicle Experiment (IRVE) Design Overview[C]. 18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Germany, 2005: 1-14.

[17]WILDE, DETLEF, WALTHER, et al. Flight Test and ISS Application of the Inflatable Reentry and Descent Technology (IRDT)[J]. Acta Astronautica, 2002: 51, 83-88.

[18]卫剑征, 谭惠丰, 王伟志, 等. 充气式再入减速器研究最新进展[J]. 宇航学报. 2013, 34(7): 881-890. WEI Jianzheng, TAN Huifeng, WANG Weizhi, et al. New Trends in Inflatable Re-entry Aeroshell[J]. Journal of Astronautics, 2013, 34(7): 881-890. (in Chinese)

Optimization on a Flexible Thermal Protection Structure of Inflatable Reentry System

HUANG Mingxing WANG Weizhi

（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

With continuous development of the space exploration, a new inflatable reentry system becomes one of hot spots of international research. On the background of inflatable reentry system, the design of flexible thermal protection structure is analyzed and optimized in this paper. Firstly, one dimensional thermal model of flexible thermal protection structure is established with referring to the typical thermal protection material and structure of IRVE. Then, based on the requirements of differential algorithm, the discretion heat transfer equations of functional layers of flexible thermal protection are derived. Under the condition of thermal capability constraint, the material and the layup number of functional layers are chosen as optimized parameters and a optimizing design program of flexible thermal protection structure is achieved under the given thermal boundary conditions. Finally, this paper proposes a differential algorithm to calculate the temperature response at various functional layers during reentry, and the results are verified by ANSYS. The results show that areal density of the optimal flexible thermal protection structure is 2.128kg/m2with the material being Nextel720, Refrasil 2000 and Upilex, and the layup number being 1, 3 and 1.

inflatable reentry; aerodynamic heat; optimized design; thermal protection; spacecraft recovery

V475.9

A

1009-8518(2016)01-0022-10

10.3969/j.issn.1009-8518.2016.01.003

黄明星，男，1989年生，2013年获得北京航空航天大学飞行器设计与工程学士学位，现在中国空间技术研究院北京空间机电研究所攻读硕士学位，研究方向为再入返回技术。E-mail: hmx1620@163.com。

（编辑：陈艳霞）

2015-08-20

载人航天预研项目