空间再入飞行器热气动弹性数值研究进展
张章 黄伟 唐明章 王伟志
(北京空间机电研究所,北京 100094)
空间再入飞行器热气动弹性数值研究进展
张章 黄伟 唐明章 王伟志
(北京空间机电研究所,北京 100094)
热气动弹性分析关系到空间再入飞行器的气动性能、结构安全和振动特性。文章对空间再入飞行器热气动弹性研究的数值方法和研究进展进行了回顾;总结了热气动弹性数值的模拟内容、气/ 固/热多物理场耦合方法和高超声速气动力、气动热求解方法等方面研究的典型成果与特点;比较了单向耦合分层求解方法与双向耦合方法在热气动弹性分析方面的优缺点,指出气动力、气动热的工程计算方法和降阶方法存在一定误差,采用时域方法求解Navier-Stokes方程的全阶模型获取气动力和气动热更为准确;并对未来的研究趋势进行了展望,提出了需要进一步深入探讨的若干问题,包括空间再入过程气/ 热/固多场耦合物理机制的准确描述、空间充气式再入减速器这类柔性结构的热气动弹性分析以及热气动弹性试验验证等三个方面。
空间再入 热气动弹性 数值研究 气/固/热耦合
0 引言
空间再入飞行器一般指的是飞行马赫数 Ma>5,冲出大气层后再次进入大气层的飞行器。返回舱、充气式再入减速器等返回型航天器以及火箭、远程弹道导弹都属于空间再入飞行器的范畴。空间再入飞行器大多以高超声速进入大气层,需要承受高温气动加热、高速气流冲击、强激波以及激波/附面层干扰、高温气流热化学反应作用的影响,其再入返回的物理过程涉及空气动力学、空气热力学和结构动力学等多学科的交叉研究,是典型的热气动弹性问题。
图1是1963年Garrick I E绘制的热气动弹性力学四面体,其中气动力、热力、弹性力、惯性力构成了该四面体的4个顶点,每3个顶点所形成的面分别代表不同的学科分支:热气动弹性静力学关注的是气动力、热力、弹性力之间的相互作用;经典气动弹性力学关注的是气动力、惯性力、弹性力之间的相互作用;空气热力学关注的是气动力、热力、惯性力的相互作用,热弹性动力学关注的是热力、弹性力、惯性力的相互作用。热气动弹性力学四面体直观地表达了气动力、弹性力、惯性力和热力的相互作用,揭示了热气动弹性力学的物理本质是气/固/热的多物理场耦合[1-2]。一方面,高超声速条件下的气动加热效应使得空间再入飞行器驻点温度变高、气动热载荷变大,极易造成结构破坏和材料特性变化;另一方面,高速气流作用下的非定常气动力和气动热载荷会导致空间再入飞行器的结构变形和气动弹性动力响应,结构变形又反过来影响飞行器的气动外形,进而造成气动力和气动热载荷的改变。以上分析说明,空间再入飞行器热气动弹性的研究模型是一个复杂的动力学系统。高超声速条件下气动加热效应不能忽略,且高温效应下再入飞行器的几何非线性和材料非线性极强,流体域气体动力学计算、固体域结构动力学仿真与气动热分析之间的反复迭代难以避免。与此同时,热气动弹性分析直接关系到空间再入飞行器的气动性能、结构安全和振动特性[3]。因此,热气动弹性研究已成为空间再入飞行器设计阶段不可忽视的重要问题。
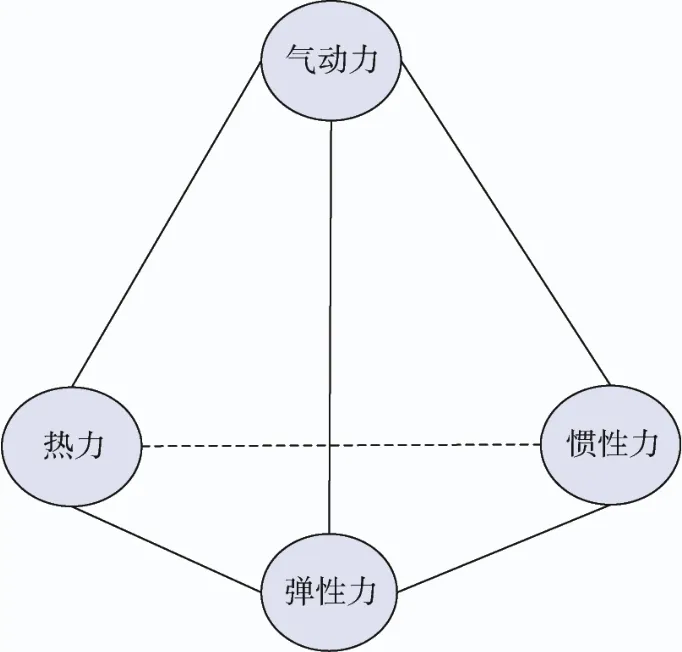
图1 热气动弹性力学四面体Fig.1 Aerothermoelastic tetrahedron
对于空间再入飞行器而言,在高声速条件下进行热气动弹性方面的缩比风洞试验难度很大,飞行测试试验成本高昂[4-5]。因此,热气动弹性的数值研究显得尤为重要。然而该方面的数值研究挑战性极大:气/固/热高耦合程度的一体化求解方法最接近热气动弹性研究的物理本质,但是它对计算资源和时间要求过高,在算法稳定性和收敛性上难度较大[6-7]。而气/固/热解耦和弱耦合的研究思路以及气动力、气动热的工程简化算法能否真实反映热载荷下气动弹性的耦合物理机制?究竟哪些因素决定着热气动弹性数值研究的精度?在上述研究背景和疑问下,本文对空间再入飞行器热气动弹性的数值研究进行回顾与总结,对其发展趋势和研究方向进行探讨和展望。
1 热气动弹性数值研究的内容
热气动弹性研究是空间再入返回物理过程中无法回避的问题。空间再入飞行器的热气动弹性数值研究有两个重要方面:第一个是气/固/热多物理场耦合体系的构建;第二个是气动力、气动热和结构动力学的计算。
为了使理论预测能够正确体现高超声速飞行器的物理特征,气/固/热多物理场耦合建模分析已成为国内外研究的热点和难点。按照热气动弹性的物理含义,气/固/热多物理场耦合模型可以分为强耦合和弱耦合;按照求解思路可以分为单向耦合和双向耦合;按照计算方法可以分为松耦合和紧耦合[8]。现阶段热气动弹性数值模拟中气动力、气动热的获取主要依靠工程近似模型、降阶模型和计算流体力学(Computational Fluid Dynamics,CFD)高精度求解方法。而在结构动力学计算方面,有限元方法在现阶段是结构热传导和动力学建模仿真的主流方法。
2 气/固/热多物理场耦合方法研究进展
热气动弹性力学涉及空气动力学、气动热力学和结构动力学等多学科交叉,因此从逻辑上讲热气动弹性力学的首要问题是如何构建气/固/热多物理场耦合体系,实现空气动力学、气动热力学和结构动力学之间的迭代计算与信息交换。气/固/热多物理场耦合方法主要包括单向耦合分层求解方法以及双向耦合求解方法,下面分别对这两种耦合方法的典型研究成果和各自特点进行总结。
2.1 热气动弹性单向耦合分层求解
2.1.1 求解流程
针对气/固/热多物理场耦合方法,由于对气/固/热多物理场耦合问题一次性完全求解难以实现,现有研究大多采用工程简化、解耦和单向耦合的思路,将热气动弹性问题分解为气动热问题和气动弹性问题两个部分[9-10]。这主要基于三点假设:一是认为结构变形产生的热量很小可以忽略;二是认为动态热气动弹性耦合程度不高,气动热系统的特征时间远大于气动弹性系统振动的时间周期;三是认为静态热气动弹性的耦合程度较低,结构弹性变形不足以改变表面温度分布[11-12]。在上述假设下,可以先进行气动加热计算得到高超声速飞行器表面温度分布,之后在该热环境下进行结构动力学计算得到刚度分布和模态频率,再通过空气动力学计算得到非定常气动力,在上述分层求解的基础上最后进行气动弹性特性分析[13-14]。上述分析流程如图2所示。

图2 热气动弹性分层求解流程Fig.2 Hierarchic solution process of aerothermoelastic analysis
2.1.2 典型研究成果
国内外诸多学者采用单向耦合分层求解的思路来探讨空间再入飞行器的热气动弹性问题。文献[15]在时域内采用分层求解的计算流程,分析了“高超声速飞行器2号”(Hypersonic Technology Vehicle 2,HTV-2)飞行器在特定飞行轨迹下的热气动弹性特性;其数值研究采用NASA兰利中心开发的CFD仿真程序CFL3D计算气动热和气动力,采用MSC. NASTRAN进行有限元的结构动力学和热力学求解,在考虑材料特性的退化和热应力的影响下对瞬时传热进行了分析。文献[16]采用单向耦合的方法对不同温度分布下翼型的热气动弹性力学特性进行了研究。文献[17]提出用四场描述的方法刻画气动热效应和气动热作用下的高超声速气动弹性问题。文献[18]采用单向耦合分层求解的数值方法研究了高超声速复合材料机翼的热气动弹性问题。文献[19]采用分层求解的思路开展了再入高超声速飞行器的热气动弹性问题的研究。文献[20]采用热气动弹性分层求解方法研究了高超声速飞行器舵面的颤振特性,得出气动加热效应能够降低高超声速飞行器的气动弹性稳定性的结论。文献[17]采用单向耦合的思路研究了平板的热气动弹性特性,但在热气动弹性分析中仅考虑温度分布所引起的结构形变与应力变化,忽略了结构变形对气动加热作用的影响。文献[21]采用准静态有限元方法进行高超声速飞行器的气动热/气动弹性耦合分析,搭建了热气动弹性单向耦合分析框架,然而由于其采用准静态方法求解气动力和气动热,因此高超声速条件下的非定常气动力与气动热载荷的求解精度不高。文献[22]采用单向耦合分层求解的方法研究再入飞行器的热气动弹性问题,运用CFD仿真程序FEFLO98进行气动力计算,采用COSMIC NASTRAN软件进行线性结构分析和热传导分析,采用DYNA3D软件进行非线性结构动力学分析。文献[23]采用分层求解方法对高超声速下翼面的热气动弹性特性进行了工程分析。文献[24]针对给定温度分布热效应下的气动弹性问题进行了数值仿真,运用单向耦合分层求解的思路分析了不同温度分布与结构支撑形式对高超声速飞行器热气动弹性特性的影响。文献[25]根据空间充气式再入结构飞行试验的测试结果给定气动力载荷和气动热载荷,开展了结构动力学计算、振动模态分析和振动响应分析,然而该研究给定的气动力、气动热载荷过于简化,且对高超声速条件下气/固/热三场耦合作用考虑不足,得到的振动响应分析结果准确性有待商榷。
2.1.3 求解方法的优、劣势
单向耦合的方法在满足一定工程精度的条件下具有高效求解热气动弹性问题的优势,在热气动弹性研究中占用计算资源少,求解效率较高,因而被研究者广泛采用。然而由于解耦和单向耦合的研究方法对不同物理场耦合作用的关注程度不高,存在诸多简化,因此对于几何非线性强、飞行马赫数高的空间再入飞行器热气动弹性问题不再完全适用,需考虑双向耦合的分析思路。
2.2 热气动弹性双向耦合
2.2.1 耦合关系
一般来说,考虑热效应的气动弹性双向耦合可以划分为气动弹性问题的流固双向耦合、气动热问题中气动加热与热传导的双向耦合以及气动热问题和气动弹性问题的相互耦合,其耦合关系如图3所示。
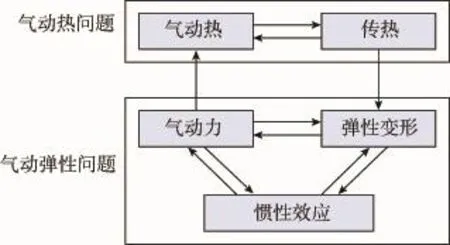
图3 热气动弹性双向耦合求解示意Fig.3 Two-way coupled aerothermoelastic analysis process
2.2.2 流固双向耦合方法的研究成果
对于柔性结构,经典的气动弹性分析方法中常用的“结构小变形条件下弹性体表面气动力与结构变形无关”的假设已经失效,可选用任意拉格朗日–欧拉法(arbitrary lagrangian-eulerian,ALE)整体求解,或流体域、固体域之间的迭代求解这两种流固耦合方式。
由于流体力学习惯采用欧拉坐标系描述流体运动,而结构力学习惯采用拉格朗日坐标系进行描述,因此如何采用统一坐标系及流固交界面的协调匹配问题成为流固耦合问题的难点。流固耦合ALE整体求解法将流体控制方程和结构动力学方程结合成一个算子,将流体和固体作为由流固交界面联系起来的统一连续介质进行时间推进求解[26]。文献[27]最先建立了任意拉格朗日–欧拉坐标系,提供了一种统一描述流体和固体的坐标形式,适用于基于有限元方法的流固耦合仿真。文献[28]运用ALE方法构建了Navier-Stokes流体控制方程下的有限元模型,发展了流固交界面不匹配网格间运动参数的传递方法。LS-DYNA商用计算软件是采用ALE整体流固耦合求解方法的典型实例,在算法时间推进上它首先进行一个或多个Lagrangian时间步长计算,然后再进行ALE流固强耦合的时间推进,可以处理空间大位移或大变形量的流固耦合问题。文献[29]采用 LS-DYNA软件建立了有限质量条件下降落伞充气过程的流固耦合数值模型,数值仿真结果与风洞试验测试结果对比良好。文献[30]采用 LS-DYNA软件对无限质量条件下的降落伞充气特性开展了流固耦合数值模拟,数值仿真得到的伞形和气动阻力与风洞试验对比良好。ALE流固耦合整体求解法将流体域、固体域离散至任意拉格朗日–欧拉坐标系中,动网格即成为运动方程的一部分而无需分开单独处理,且流体、固体求解完全同步,不存在时间延迟和能量不守恒的缺陷。然而ALE流固耦合整体求解法对计算资源要求过高,在准确描述高超声速流动上存在困难,在算法稳定性上也亟需突破。
流固双向迭代耦合在机翼、舵面、叶轮机械的飞行器气动弹性研究中应用较多,已形成比较成熟的数值工具。流固双向迭代耦合通过在流体域和固体域各自求解动力学方程得到流场和结构参数,之后并不直接推进到下一时间步,而是将流体域和固体域进行相互迭代计算,直至满足几何守恒、动量守恒的收敛条件时才进行物理时间步的推进。商用计算软件ANSYS中的双向迭代耦合求解流程如图4所示。文献[31]在热气动弹性耦合求解研究中考虑了结构变形与气动压力之间的相互迭代关系,先计算初始结构壁面气动压力,之后进行结构响应分析,更新结构变形后再与气动压力进行迭代直至满足收敛条件。文献[32]采用流固迭代耦合的方法对AGARD445.6翼型进行了气动弹性研究,采用LU-SGS隐式算法和隐式线性多步算法在每一个物理时间步交叉求解结构动力学方程和气动控制方程。文献[33]利用流固迭代耦合方法在时域内求解超声速舵面的气动弹性稳定性问题。流固双向迭代耦合较流固解耦方法和流固弱耦合方法计算精度有所提高,可以用于空间再入飞行器一定变形范围内的气动弹性分析。然而流固双向迭代耦合所需的动网格技术对流体域、固体域动边界的刻画需要占据一定的计算资源,在气动弹性数值仿真中每一步时间推进都需要重构贴体网格,因此需要较长的计算时间。

图4 流固双向迭代耦合求解示意Fig.4 Two-way coupled analysis process of fluid structure interaction
2.2.3 气动热问题的双向耦合研究成果
气动热问题的双向耦合主要由气动加热和结构热传递之间的计算构成,针对简单几何外形(如壁板)的气动热计算多采用工程算法估计结构表面温度分布,再与传热分析、热结构分析进行耦合求解。文献[34]通过求解Navier-Stokes方程得到气动热,并通过准静态有限元方法进行CFD-CTSD联合分析来描述气动热与传热的双向耦合作用。文献[9]采用 CFD方法求解气动热问题,采用有限元方法进行传热分析和热结构分析,考虑了高超声速气流与结构之间的热传导作用。文献[35]采用基于CFD定常流动分析的热传导计算,得到高超声速飞行器结构温度场分布后再求解其气动弹性特性。文献[36]将气动热计算与传热计算得到的不同温度分布引入结构动力学热刚度计算,考察了高超声速飞行器翼面的热气动弹性特征。文献[37]对高超声速飞行器的热气动弹性特性进行了研究,通过气动加热和传热计算获得热载荷,再作为输入条件进行考虑热效应的气动弹性分析,得出热效应会导致高超声速飞行器气动弹性稳定性恶化的结论。
2.2.4 气动弹性问题与气动热问题的耦合关系
除此之外,在气动热求解得到结构温度分布传递至气动弹性计算的同时,如何考虑弹性变形对气动热计算的影响是真实描述气动热问题和气动弹性问题耦合关系的难点。文献[38]针对半无限大平板的热气动弹性特性建立了气/热/固双向耦合数值模型,研究表明:考虑弹性变形的气动热计算使热流发生了非均匀变化,进而导致结构表面温度分布的不均匀变化和材料非线性特征变强,对气动弹性稳定性和结构响应产生一定的影响,但其对高超声速流动和气动热计算的简化在精度方面尚值得商榷。文献[39]针对高超声速再入飞行器壁板的热气动弹性特征构建了气/热/固多物理场耦合体系,对比了考虑弹性变形对气动热影响的双向耦合模型与单向耦合模型的求解精度,分析了上述两种耦合方式对颤振和结构响应的影响。尽管已有研究者证明弹性变形对气动热的反馈作用不应被忽略,然而受制于双向耦合建模的复杂性及计算资源的有限性,当前大部分热气动弹性数值研究仍采用忽略弹性变形对气动热计算影响的单向耦合方法。
综上所述,针对空间再入飞行器的热气动弹性特征,应重点开展紧耦合层面上的流固双向迭代耦合建模,松耦合层面上的气动热、传热双向耦合计算,采用合理简化方法考察柔性结构弹性变形对气动加热作用的影响,实现考虑热效应的气动弹性双向耦合体系的构建。
3 高超声速气动力求解方法研究进展
空间再入过程中涉及的高超声速流动具有流场非线性特征强,激波强度高,存在化学反应边界层、高熵层和薄激波层,大气低密度及真实气体效应不能忽略等特点,因此气体动力学计算至关重要[40]。高超声速流动的数值模拟与热气动弹性研究中非定常气动力的准确获取息息相关。受制于计算资源和时间的限制,现有研究多采用气动力的工程计算方法或降阶方法。
气动力的典型工程计算方法有活塞理论、当地流活塞理论、Van Dyke二阶理论、激波/膨胀波理论、牛顿冲击流理论和升力面理论[41]。活塞理论是频域计算气动力应用最广泛的一种方法,它适用于薄翼型飞行器和飞行马赫数Ma>1的情况下的非定常气动力计算。当地流活塞理论指的是采用定常流动计算得到的当地流场参数来代替活塞理论中的自由流参数,其适用于求解尖前缘物面几何形式的大迎角问题。文献[13]采用基于欧拉方程的CFD定常流动计算得到当地流场参数,使得当地流活塞理论在马赫数达到10时仍然适用。文献[42]总结了Van Dyke二阶理论、激波/膨胀波理论、牛顿冲击流理论估算高超声速飞行器气动力的研究进展和适用范围。文献[43]最早提出了基于统一升力面理论的非定常气动力求解方法,其适用的马赫数范围较宽,在考虑了几何物面厚度的同时考虑了上洗流的影响,相对于时域求解Navier-Stokes方程的CFD方法具有计算速度快和能够考虑小迎角条件等特点。上述工程算法多假设流体无粘且忽略真实气体效应,计算效率高但只在特定条件下满足一定的工程精度,在空间再入飞行器的热气动弹性分析中无法提供精确的气动力输入。气动力降阶方法的思路是根据若干全阶气动力求解全阶模型的采样结果来确定整个系统的主要特征,其精度与全阶求解模型相比有所下降,但计算耗费大大降低。经典的气动力降阶方法主要有特征正交分解法(proper orthogonal decomposition,POD)、Volterra法、代理函数法。运用气动力降阶方法进行空间再入飞行器和高超声速飞行器求解的主要研究有:文献[44]采用POD气动力降阶方法预测了X-34再入飞行器的表面压力分布,考察了高超声速下强激波对POD气动力降阶方法求解精度的影响。文献[45]采用POD气动力降阶方法研究了高超声速流场非线性效应对降阶模型的影响。文献[46]针对X-43再入飞行器的热气动弹性分析发展了基于自回归平均模型的代理函数法来求解气动力,在满足热气动弹性工程分析精度的基础上较大地提高了计算效率。文献[47]采用基于Kriging代理函数的气动力降阶方法来求解高超声速条件下的气动力问题并与POD气动力降阶方法进行对比,结果显示Kriging代理函数法相对POD降阶方法拥有更高的精确度。
由于降阶理论主要基于线化假设,且高超声速流动速度扰动大,控制方程中非线性特征项需要保留,因此时域求解Navier-Stokes方程的全阶CFD模型在理论上更为精确。文献[48]对比了一阶、三阶活塞理论与直接求解Navier-Stokes方程的CFD方法获得气动力进行气动弹性分析的差异,结果表明:在三维流动作用明显、高超声速流场非线性较强时,气动弹性分析需使用 CFD方法求解考虑高温效应的Navier-Stokes方程,获得非定常气动力。文献[49]运用CFD方法求解三维可压缩的Navier-Stokes方程对HYFLEX再入飞行器的气动特性进行了数值研究,结果与飞行试验数据对比良好。然而,采用CFD全阶模型时域求解气动力存在计算量大、计算效率低的问题。文献[50]在CFD时域计算中引入自回归移动平均法进行频率和阻尼识别,提高了全阶CFD模型的计算效率。如何处理高超声速热效应下化学反应非平衡流是空间再入飞行器气动计算的难点。文献[51]采用CFD时域求解Navier-Stokes方程方法对比了理想气体与考虑化学反应非平衡流对高超声速气动弹性稳定性的影响,结果表明粘性效应及高超声速热效应均会对再入飞行器的气动弹性稳定性产生影响。文献[52]以类“阿波罗”返回舱外形为研究对象,利用H3NS和DSMC计算程序时域求解Navier-Stokes方程的方法对气动力进行了研究,比较了量热完全气体、多组分化学反应气体及稀薄气体流动的计算结果,探讨了有限速率化学反应模型及壁面催化特性的影响。
综合上述分析可知,在气动力的求解上,工程近似模型和降阶模型相对简单,模型本身存在误差,获取的气动力精确度不高,对空间再入飞行器的热气动弹性分析不利,需要时域求解考虑化学反应非平衡流的Navier-Stokes方程加以改善。
4 高超声速气动热求解方法研究进展
高超声速气动热求解方法包括气动热工程计算方法、降阶方法以及CFD高精度求解方法。对于存在相似解的平板扰流问题,一般采用Eckert参考焓法、Spalding-Chi法、Van Driest法、Zoby雷诺比拟法获得表面热流密度。对于不存在相似解的简单几何气动热求解,通常采用Lees公式、Fay-Riddell公式和Scala公式等计算得到表面热流密度[53]。高超声速气动热求解的一个重要问题是要考虑高超声速热效应下化学反应的影响。文献[54]采用Park双温模型对“阿波罗”返回舱进行了气动热计算,其数值计算结果与飞行试验数据相吻合。文献[55]针对轴对称钝头体进行气动热工程计算,考虑了化学反应及攻角的影响,得到的数值结果与试验对比良好。文献[56] 涙研究了边界层转 对返回舱热防护面的影响,得到发生在热防护面的边界层 涙转 影响热防护层厚度的结论。文献[57]采用双温度模型、三温度模型作为分析化学反应非平衡流的工具,计算了空间再入飞行器高超声速条件下的气动热,得出热力学非平衡效应导致再入飞行器压心前移,壁面催化条件对表面热流影响明显的结论。气动热的工程计算方法多适用于简单几何的超声速飞行器表面热流的求解,它具有计算效率高的优势,但气动热求解模型通用性差,模型本身存在误差,对气动热的求解精度不高。
气动热的降阶求解方法主要采用正则正交分解法(POD法)和代理函数法:POD法是用全阶模型的响应快照中计算得到一组正交基,并由此得到气动热降阶模型;代理函数法用计算效率较高的非线性函数近似表示气动热的全阶数值仿真模型。文献[44]采用POD气动力降阶方法预测了X-34再入飞行器的表面温度分布。文献[58]采用Kriging代理函数法构建高超声速热流求解模型,具有考虑任意物面表面温度分布的能力。文献[8]运用Kriging代理函数法进行气动热降阶,对高超声速翼面气/热/固三场耦合特性进行了分析。
气动热的CFD求解方法是通过全阶模型直接求解Navier-Stokes方程,并将考虑真实气体效应的热力学函数关系式引入高超声速气动热的数值计算中。文献[59]采用CFD方法直接求解Navier-Stokes方程得到表面压力和气动热,之后对高超声速机翼进行了热气动弹性分析得出机翼变形会导致激波结构及加热速度分布改变的结论。文献[60]通过求解二维Navier-Stokes方程探讨气动热问题,讨论了Roe的FDS 和AUSM+空间离散格式对高超声速钝头体热流密度计算数值精度的影响。文献[61]运用GASP程序求解Navier-Stokes方程的方法对空间再入飞行器X-43进行了气动热数值模拟研究,但数值结果与试验偏差较大。文献[62]采用CFD方法对高超声速热化学平衡流进行了数值模拟计算并分析了Roe、AUSM、NND格式的计算效果。文献[63]采用CFD方法对火星“探路者”号进入舱试验模型进行了数值模拟研究,结果表明热完全气体模型和量热完全气体模型在驻点处和流动分离区的热流密度估计上存在较大差别。文献[64]运用 CFD方法对包含 Park双温模型、Gupta空气多组分和有限速率的化学反应模型的全Navier-Stokes方程进行求解来获得气动热,发展了带有源项的LU-SGS数值求解方法来提高计算效率。文献[65]采用CFD方法对三维钝锥模型的表面热流进行了数值模拟研究,得出来流参数、物面密度、攻角和特征长度是影响热流密度计算的主要因素。文献[66]采用标量对角化隐式 NND格式来求解Navier-Stokes方程,运用数值模拟手段分析了影响空间再入飞行器表面热流准确性的因素。文献[67]用高精度TVD格式的CFD方法求解雷诺平均Navier-Stokes方程,发展了气动热与结构传热的耦合计算方法。
综合上述分析可知,在气动力热的求解上,工程近似模型和降阶模型相对简单,模型本身存在误差,获取的气动热结果精确度不高,对空间再入飞行器的热气动弹性分析不利,需要时域求解考虑化学反应非平衡流的Navier-Stokes方程加以改善。
5 研究趋势展望
综合国内外学者对空间再入飞行器热气动弹性力学的数值研究状况,笔者认为在以下三个方面还需深入:
1)如何准确描述空间再入飞行器气/固/热多物理场耦合的物理机制?目前热气动弹性的研究大多采用解耦和单向耦合的思路加以简化,受制于计算资源和时间的限制,在气动力、气动热的求解上亦采用工程简化模型和降阶策略,在牺牲部分精度的前提下进行分析。热气动弹性问题的物理本质是气动力、弹性力、惯性力和热力的耦合作用,而对其物理机制探索的关键在于气/热/固多物理场耦合体系的合理构建以及气动力、气动热载荷等外作用力的精确求解。高超声速条件下热非定常气动力、气动热载荷和热结构动力学特性的变化规律和内在联系是什么?如何运用双向耦合的思路克服现有研究气/热/固耦合程度不高,气动力、气动热求解不准确的问题?上述这些问题将是空间再入飞行器热气动弹性机理研究的热点问题。
2)针对充气式再入减速器这类新型空间再入飞行器,如何提取柔性充气结构的特征模型进行热气动弹性分析?现有的热气动弹性研究多针对常规弹性固体结构进行气/固/热耦合建模分析。然而常规弹性固体结构的热气动弹性数值研究方法对空间充气式再入减速器这类柔性充气结构并不一定适用。如何针对充气柔性结构进行结构动力学建模?充气结构内部气体如何参与到气/固/热多物理场耦合分析中?另外,对空间再入柔性充气结构的非线性大变形和热冲击响应的分析方法也需要进一步探索。
3)热气动弹性数值研究的相关试验验证。空间再入飞行器的热气动弹性数值研究离不开试验验证。由于高声速条件下进行热气动弹性方面的缩比风洞试验难度大、费用高,飞行测试试验成本高昂,导致目前空间再入飞行器的热气动弹性试验研究相对不足。积极开展热环境下的振动模态试验、地面半实物仿真试验、模拟高焓高速流场条件的风洞试验以及飞行试验对空间再入飞行器的机理研究及工程应用都有着十分重大的意义。
References)
[1]陈桂斌, 杨超, 邹丛青. 气动弹性设计基础[M]. 第2版. 北京: 北京航空航天大学出版社, 2010: 6-7. CHEN Guibin, YANG Chao, ZOU Congqing. Basis of Aeroelastic Design[M]. 2nd Edition. Beijing: Beihang University Press, 2010: 6-7. (in Chinese)
[2] GARRICK I E. Prospects for the Aerothermoelasticity[J]. Aerospace Engineering, 1963, 22(1): 140-147.
[3] MURMAN S M. Dynamic Simulations of Atmospheric-entry Capsules[J]. Journal of Spacecraft and Rockets, 2009, 46(4): 829-835.
[4] LICHODZIEJEWSKI L, KELLEY C, TUTT B, et al. Design and Testing of the Inflatable Aeroshell for the IRVE-3 Flight Experiment[C]. 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, United States, 2012.
[5]HUGHES S J, CHEATWOOD D F, DILLMAN R A, et al. Hypersonic Inflatable Aerodynamic Decelerator (HIAD) Technology Development Overview[C]. 21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Dublin, Ireland, 2011.
[6] BAGINSKI F, BRAKKE K. Deployment Analysis of Pneumatic Envelopes Including Ascending Balloons and Inflatable Aerodynamic Decelerators[J]. Journal of Spacecraft and Rockets, 2012, 49(2): 413-421.
[7]张章, 侯安平, 脱伟, 等. 航空发动机叶片气动弹性动力响应的数值方法研究进展[J]. 力学进展, 2012, 42(5): 572-582. ZHANG Zhang, HOU Anping, TUO Wei, et al. A Review of Numerical Research on Aeroelastic Dynamical Response of Aero-engine Blades[J]. Advances in Mechanics, 2012, 42(5): 572-582. (in Chinese)
[8]李国曙. 高超声速飞行器气动–热–结构耦合分析方法研究[D]. 北京: 北京航空航天大学, 2013. LI Guoshu. Aero-thermo-structure Coupling Mechanism Research on Hypersonic Vehicles[D]. Beijing: Beijing University of Acronautics and Astronautics, 2013. (in Chinese)
[9]MCNAMARA J J, FRIEDMANN P P, POWELL K G, et al. Aeroelastic and Aerothermoelastic Behavior in Hypersonic Flow[J]. AIAA Journal 2008, 46(10): 2591-2610.
[10]FAZELZADEH S A, HOSSEINI M. Aerothermoelastic Behavior of Supersonic Rotating Thin-walled Beams Made of Functionally Graded Materials[J]. Journal of Fluids and Structures, 2007, 23(8): 1251-1264.
[11]MCNAMARA J J, FRIEDMANN P P. Aeroelastic and Aerothermoelastic Analysis in Hypersonic Flow: Past, Present, and Future[J]. AIAA Journal, 2011, 49(6): 1089-1122.
[12]MCNAMARA J J, ADAM J C, ANDREW R C. Aerothermoelastic Modeling Considerations for Hypersonic Vehicles[C]. AIAA 2009-7397, 2009.
[13]杨超, 许贇, 谢长川. 高超声速飞行器气动弹性力学研究综述[J]. 航空学报, 2010, 31(1): 1-11. YANG Chao, XU Yun, XIE Changchuan. Review of Studies on Aeroelasticity of Hypersonic Vehicles[J]. Acta Aeronautica ET Astronautica Sinica, 2010, 31(1): 1-11. (in Chinese)
[14]程兴华. 高超声速飞行器防热壁板气动热弹性耦合建模与分析[D]. 长沙: 国防科学技术大学, 2012.CHENG Xinhua. Coupled Aerothermoelastic Modeling and Analysis of Thermal Protection Panel for Hypersonic Vehicles[D]. Changsha: National University of Defense Technology, 2012. (in Chinese)
[15]MCNAMARA J J. Aeroelastic and Aerothermoelastic Behavior of Two and Three Dimensional Lifting Surfaces in Hypersonic Flow[D]. United States: University of Michigan, 2005.
[16]ROGERS J P. Aerothermoelastic Analysis of a NASP-like Vertical Fin[C]. 33rd AIAA/ASME/ ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Dallas, United States, 1992.
[17]TRAN H, FARHAT C. An Integrated Platform for the Simulation of Fluid-structure-thermal Interaction Problems[C]. 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Denver, United States, 2002.
[18]POLLI G M, MASTRODDI F, LIBRESCU L, et al. Aerothermoelastic Stability of Composite Aerovehicle Wings Subjected to Heat Inputs[J]. AIAA Journal, 2008, 46(4): 992-1001.
[19]FRIEDMANN P P, MCNAMARA J J, THURUTHIMATTAM B J, et al. Hypersonic Aerothermoelasticity with Application Reuseable Launch Vehicles 2003[C]. 12th AIAA International Space Planes and Hypersonic Systems and Technologies, Norfolk, United States, 2003.
[20]ERICSSON L E, ALMROTH B O, BAILIE J A. Hypersonic Aerothermoelastic Characteristics of a Finned Missile[J]. Journal of Aircraft, 1979, 16(3): 187-192.
[21]THORNTON E A, DECHAUMPHAI P. Coupled Flow, Thermal and Structural Analysis of Aerodynamically Heated Panels[J]. Journal of Aircraft, 1988, 25(11): 1052-1059.
[22]LOHNER R, YANG C, CEBRAL J, et al. Fluid-structure-thermal Interaction Using a Loose Coupling Algorithm and Adaptive Unstructured Grids[C]. Proceedings of the 29th AIAA Fluid Dynamics Conference, Albuquerque, United States, 1998.
[23]吴志刚, 惠俊鹏, 杨超. 高超声速下翼面的热颤振工程分析[J]. 北京航空航天大学学报, 2005, 31(3): 270-273. WU Zhigang, HUI Junpeng, YANG Chao. Hypersonic Aerothermoelastic Analysis of Wings[J]. Journal of Beijing University of Aeronautics and Astronautics, 2005, 31(3): 270-273. (in Chinese)
[24]张伟伟, 夏巍, 叶正寅. 一种高超音速热气动弹性数值研究方法[J]. 工程力学, 2006, 23(2): 41-46. ZHANG Weiwei, XIA Wei, YE Zhengyin. A Numerical Method for Hypersonic Aerothermo-elastic[J]. Engineering Mechanics, 2006, 23(2): 41-16. (in Chinese)
[25]LINDELL M C, HUGHES S J, DIXON M, et al. Structural Analysis and Testing of the Inflatable Re-entry Vehicle Experiment (IRVE)[C]. 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Newport, United States, 2006.
[26]MOHD F, ASHARF A O, WAQAR A. Arbitrary Lagrangian-eulerian Form of Flowfield Dependent Variation Method for Moving Boundary Problems[C]. 32nd AIAA Applied Aerodynamics Conference, Atlanta, United States, 2014.
[27]HIRT C W, AMSDEN A A, COOK J L. An Arbitrary Lagrangian-eulerian Computing Method for All Flow Speeds[J]. Journal of Comp. Phys., 1974, 14: 227-253.
[28]谢浩. 三维非线性动态流体—结构耦合数值方法及其应用研究[D]. 西安: 西安交通大学, 2003. XIE Hao. Numerical Simulation and Application Research on 3-dimensional Nonlinear Dynamic Fluid-structure Interaction[D]. Xian: Xian Jiaotong University, 2003. (in Chinese)
[29]TUTT B A, TAYLOR A P, ANTHONY P. The Use of Ls-Dyna to Simulate the Inflation of a Parachute Canopy[C]. 18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Munich, Germany, 2004.
[30]COQUET Y, BORDANAVE P. Improvements in Fluid Structure Interaction Simulation of Parachute Using Ls-Dyna[C]. 21th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Dublin, Ireland, 2011.
[31]ADAM J C. Coupled Fluid-thermal-structural Modeling and Analysis of Hypersonic Flight Vehicle Structures[D]. United States: Ohio State University, 2010.
[32]肖军, 谷传纲. 基于全隐式紧耦合算法的颤振数值分析[J]. 机械工程学报, 2010, 46(22): 156-174. XIAO Jun, GU Chuangang. Numerical Analyses for Flutter Based on Fully-implicit Tightly-coupled Algorithm[J]. Journal of Mechanical Engineering, 2010, 46(22): 156-174. (in Chinese)
[33]蔡天星, 徐敏, 姚伟刚, 等. 基于CFD/CSD耦合的超声速舵面动载荷计算[J]. 工程力学, 2011, 28(3): 245-250. CAI Tianxing, XU Min, YAO Weigang, et al. Transient Load on Supersonic Fin Analysis Based on CFD/CSD Coupling[J]. Engineering Mechanics, 2011, 28(3): 245-250. (in Chinese)
[34]WIETING A R, DECHAUMPHAI P, BEY K, et al. Application of Integrated Fluid- thermal-structure Analysis Methods[R].NASA TM 100625, 1988.
[35]GUPTA K K, CHOI S B, IBRAHIM A. Development of an Aerothermalelastic-acoustics Simulation Capability of Flight Vehicles[C]. 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Oriando, United States, 2010.
[36]李增文, 林立军, 关世义. 超声速全动翼面热颤振特性分析[J]. 战术导弹技术, 2008, 1(5): 36-39. LI Zengwen, Lin Lijun, GUAN Shiyi. Research on the Thermal Flutter Characteristics of Hypersonic All-move Wing[J]. Tactical Missile Technology, 2008, 1(5): 36-39. (in Chinese)
[37]吕继航, 杨茂, 陈凤明. 超音速舵面热气动弹性仿真[J]. 计算机仿真, 2010, 27(3): 43-46. LV Jihang, YANG Mao, CHEN Fengming. Aerothermoelastic Simulation of Supersonic Missile Rudder[J]. Computer Simulation, 2010, 27(3): 43-46. (in Chinese)
[38]ADAM J C, MCNAMARA J J. Studies on Fluid-thermal-structural Coupling for Aerothermoelasticity in Hypersonic Flow[J]. AIAA Journal, 2010, 48(8): 1721-1723.
[39]YANG Chao, LI Guoshu, WAN Zhiqiang. Aerothermal-aeroelastic Two-way Coupling Method for Hypersonic Curved Panel Flutter[J]. Science China-technological Sciences, 2012, 55(3): 831-840.
[40]MUHARREM O, SINAN E. Analysis of Hypersonic Flow Using Three Dimensional Navier–Stokes Equations[C]. 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, United States, 2014.
[41]安效民, 徐敏, 陈士橹. 多场耦合求解非线性气动弹性的研究综述[J]. 力学进展, 2009, 39(3): 284-298. AN Xiaomin, XU Min, CHEN Shilu. An Overview of CFD/CSD Coupled Solution for Nonlinear Aeroelasticity[J]. Advances in Mechanics, 2009, 39(3): 284-298.
[42]JAZRA T, PRELLER D, SMART M K. Design of an Airbreathing Second Stage for a Rocket-scramjet-rocket Launch Vehicle[J]. Journal of Spacecraft and Rockets, 2013, 50(2): 411-422.
[43]LIU D D, CHEN P C, TANG L, et al. Hypersonic Aerothermodynamics/Aerothermoelastics Methodology for Reusable Launch Vehicles/ TPS Design and Analysis[C]. 41st Aerospace Sciences Meeting and Exhibit, Reno, United States, 2003.
[44]TANG L, CHEN P, LIU D D, et al. Proper Orthogonal Decomposition and Response Surface Method for TPS/RLV Structural Design and Optimization: X-34 Case Study[C]. 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, United States, 2005.
[45]LUCIA D J. Reduced Order Modeling for High Speed Flows with Moving Shocks[D]. United States: Air Force Institute of Technology, Wright-patterson AFB, 2001.
[46]GUPTA K K, BACH C. Systems Identification Approach for a Computational-fluid-dynamics based Aeroelastic Analysis[J]. AIAA Journal, 2007, 45(12): 2820-2827.
[47]CROWELL A R, MCNAMARA J J, KECSKEMETY K M, et al. A Reduced Order Aerothermodynamic Modeling Framework for Hypersonic Aerothermoelasticity[R]. 51st AIAA/ASME/ASCE/AHS/ASC Structural Dynamics and Materials Conference, Orlando, United States, 2010.
[48]THURUTHIMATTAM B J. Fundamental Studies in Hypersonic Aeroelasticity Using Computational Methods[D]. United States: University of Michigan, 2005.
[49]郝子辉, 王立宁, 阎超. HYFLEX气动力/热特性数值模拟研究[C]. 第十六届全国计算流体力学会议论文集, 厦门, 2014. HAO Zihui, WANG Lining, YAN Chao. Numerical Research on Aerodynamic/Heat Performance of HYFLEX[C]. 16th National Computational Fluid Dynamics Conference, Xiamen, 2014. (in Chinese)
[50]MCNAMARA J J, FRIEDMANN P P, POWELL K G. Three-dimensional Aeroelastic and Aerothermoelastic Behavior in Hypersonic Flow[C]. 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conferences, Austin, United States, 2005.
[51]张兵, 韩景龙. 多场耦合计算平台与高超音速热防护结构传热问题研究[J]. 航空学报, 2011, 32(3): 400-409. ZHANG Bing, HAN Jinglong. Multi-field Coupled Computing Platform and Thermal Transfer of Hypersonic Thermal Protection Structures[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(3): 400-409. (in Chinese)
[52]PEZZELLA G, VOTTA R. Finite Rate Chemistry Effects on the High Altitude Aerodynamics of an Apollo-shaped Reentry Capsule[C]. 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, Bremen, United States, 2009.
[53]KUMAR C S, REDDY K J. Experimental Investigation of Heat Fluxes in the Vicinity of Protuberances on a Flat Plate at Hypersonic Speeds[J]. Journal of Heat Transfer, 2013, 135(12): 17011-17019.
[54]HASSAN B, CANDLER G V, OLYNICK D R. The Effect of Thermo-chemical Nonequilibrium on the Aerodynamics of Aerobraking Vehicles[C]. 27th AIAA Thermophysics Conference, Nashiville, United States, 1992.
[55]RILEY C J, DEJARNETTE F R. An Engineering Aerodynamic Heating Method for Hypersonic Flow[C]. 30th AIAA Aerospace Sciences Meeting and Exhibit, Reno, United States, 1992.
[56]STEVEN P S. Laminar-turbulent Transition on Reentry Capsules and Planetary Probes[C]. 35th AIAA Fluid Dynamics Conference and Exhibit, Toronto, Canada, 2005.
[57]李海燕. 高超声速高温气体流场的数值模拟[D]. 绵阳: 中国空气动力研究与发展中心, 2007. LI Haiyan. Numerical Simulation on Hypersonic and High Temperature Gas Flowfields[D]. Mianyang: China Aerodynamics Research and Development Center, 2007. (in Chinese)
[58]MCNAMARA J J, CROWELL A R, FRIEDMANN P P, et al. Approximate Modeling of Unsteady Aerodynamics for Hypersonic Aeroelasticity[J]. Journal of Aircraft, 2010, 47(6): 1932-1945.
[59]THORNTON E A. Thermal Structures: Four Decades of Progress[J]. Journal of Aircraft, 1992, 29(3): 485-498.
[60]LEE L H, RHO O H. Numerical Analysis of Hypersonic Viscous Flow around a Blunt Body Using Roe’s FDS and AUSM+Scheme[C]. 28th AIAA Fluid Dynamic Conference, Snowmass Village, United States, 1997.
[61]SCOTT A B, AARON H A, AUTHUR D D, et al. Hypersonic Boundary-layer Trip Development for Hyper-X[C]. 18th AIAA Applied Aerodynamics Conference, Denver, United States, 2000.
[62]柳军, 乐嘉陵, 杨辉. 高超声速圆球模型飞行流场的数值模拟和实验验证[J]. 流体力学实验与测量, 2002, 16(1): 67-79. LIU Jun, LE Jialing, YANG Hui. Numerical Simulation of Hypersonic Flowfield around Sphere Model and Experimental Verification[J]. Experiments and Measurements in Fluid Mechanics, 2002, 16(1): 67-79. (in Chinese)
[63]夏刚, 程文科, 秦子增. Spalart Allmars湍流模型在高超声速气动加热计算中的应用[J]. 国防科技大学学报, 2002, 24(6): 15-18. XIA Gang, CHENG Wenke, QIN Zizeng. Application of the Spalart-Allmars Turbulence Model in Hypersonic Aerothermodynamics Computation[J]. Journal of National University of Defense Technology, 2002, 24(6): 15-18. (in Chinese)
[64]潘沙. 高超声速气动热数值模拟方法及大规模并行计算研究[D]. 长沙: 国防科技大学, 2010. PAN Sha. Hypersonic Aerothermal Numerical Simulation Method and Massive Parallel Computation Research[D]. Changsha: National University of Defense Technology, 2010. (in Chinese)
[65]阎超, 禹建军, 李君哲. 热流CFD计算中格式和网格效应若干问题研究[J]. 空气动力学学报, 2006, 24(1): 125-130. YAN Chao, YU Jianjun, LI Junzhe. Scheme Effect and Grid Dependency in CFD Computations of Heat Transfer[J]. ACTA Aerodynamic Sinica, 2006, 24(1): 125-130. (in Chinese)
[66]贺国宏, 高晓成, 庞勇. 高超声速再入体表面热流数值模拟研究[J]. 空气动力学学报, 2001, 19(2): 177-185. HE Guohong, GAO Xiaocheng, PANG Yong. Numerical Study of Heat Transfer Predictions for Hypersonic Reentry Bodies[J]. ACTA Aerodynamic Sinica, 2001, 19(2): 177-185. (in Chinese)
[67]吴杰. 基于OpenGL的复杂外形气动加热数值模拟平台的研究与开发[D]. 上海: 上海交通大学, 2003. WU Jie. Numerical Simulation Design Platform Using OpenGL System[D]. Shanghai: Shanghai Jiaotong University, 2003. (in Chinese)
A Review of Aerothermoelastic Numerical Research on Space Reentry Vehicles
ZHANG Zhang HUANG Wei TANG Mingzhang WANG Weizhi
(Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)
Aerothermoelastic research is a major concern for aerodynamic performance, structure safty and vibration characteristics of a space reentry vehicle. A review of numerical research on space reentry vehicle aerothermoelasticity is presented in this paper, including typical investigation on aero-thermo-structure coupling and computation method of unsteady aerodynamics and aerothermodynamics in hypersonic flow. Furthermore,a comparison between one-way coupling and two-way coupling method is conducted in this paper, which points out that both engineering simplified calculation method and order-reduced method have some error in aerodynamic and aerothermodynamic calculation, while a computational fluid dynamic model to solve Navier-Stokes equation in time domain is more accurate in aerodynamic and aerothermodynamic numerical simulation. Finally, several possible aerothermoelastic research trends are also discussed. Aero-thermo-structure coupling mechanism, and flexible structure aerothermoelasticity analysis such as inflatable space reentry aeroshell are valuable in further study. And more attention should be paid to hypersonic experimental research to validate accuracy of numerical aerothermoelastic analysis.
space reentry; aerothermoelastic; numerical research; aero-thermo-structure coupling
V211.3
: A
: 1009-8518(2016)01-0010-12
10.3969/j.issn.1009-8518.2016.01.002
张章,男,1986年生,2014年获北京航空航天大学流体机械及工程专业工学博士学位,工程师。主要研究方向为航天器返回与着陆技术及气动弹性力学。E-mail:xiaodanni198649@sina.com。
(编辑:陈艳霞)
2015-10-19
载人航天预研项目

