JPEG2000压缩模拟的残余条纹成因分析

郑柯 廖耀庭 胡振龙

（中国天绘卫星中心，北京 102102）

JPEG2000压缩模拟的残余条纹成因分析

郑柯 廖耀庭 胡振龙

（中国天绘卫星中心，北京 102102）

基于某些光学遥感卫星图像相对辐射校正效果不理想，存在残余细条纹现象，文章以JPEG2000压缩为例，分析了图像压缩对相对辐射校正的不利影响。首先对相对辐射校正残余条纹的成因进行了傅里叶分析，然后利用 JPEG2000压缩器，对样本图像进行了模拟压缩——解压模拟实验和信息损失分析，实验结果证实了傅里叶分析的结论：在图像压缩比过大的情况下，相对辐射校正难以取得满意的效果，残余条纹现象可能产生。最后利用频率域空间特性量化分析残余条纹和图像信息的方法，定量分析了图像压缩对相对辐射校正的不利影响，结果表明：在采用有损压缩的前提下，降低图像压缩比并不能从根本上解决残余条纹问题，而星上相对辐射校正是彻底的解决相对辐射校正残余条纹的更优方案。

图像压缩 压缩比 星上辐射校正 相对辐射校正 航天遥感

0 引言

相对辐射校正参数定标的方案包括两类：实验室积分球定标和在轨定标[1]。地面实验室积分球数据分析表明，感光探元对入瞳光输出响应线性度良好[2]。利用实验室测定的输入光强和输出像素灰度的关系，求解灰度响应统一化参数。

由于卫星入轨工作后感光探元响应变化，实验室定标的参数无法长期适用，为此卫星数据地面处理软件多采用在轨辐射定标法，包括定标灯法、均匀场法和统计法等[3-6]。

定标灯法利用地影区的摄影，直接测定暗电流的DN值和响应系数；均匀场法则通过摄影灰度一致性较好的“均匀场”地物，通过均匀一致化方法，求解各感光探元线性响应改正系数。这两种方法均基于一阶线性响应的假设，不适应局部灰度区间的非线性响应。

为解决局部灰度区间的非线性响应问题，在实验室定标数据失效的情况下，可采用统计法定标非线性响应[7]。统计法假定在长期摄影中每个感光探元受到的光照概率密度函数相同，再基于矩匹配法、均衡法、直方图匹配等求解一致化响应改正参数。这类方法能求解全部灰度区间的改正参数，适用非线性响应参数的求解，是大多数地面处理软件采用的方案。

然而，在实际应用中部分光学遥感卫星使用上述几种相对辐射校正算法可能达不到理想状态，图像中局部区域还存在轻微的条纹[8]，这种经过相对辐射校正后仍存在轻微条纹的现象本文称作相对辐射校正残余条纹（简称残余条纹），下面两种情形容易出现残余条纹：

1）图像反差较小、地物纹理少的区域（下文称作均匀场区域）；

2）压缩比较大的遥感卫星图像。

国内外遥感卫星所采用的压缩算法主要包括DPCM、DCT、ADPCM、SPIHT、JPEG2000等[9]。其中，基于小波压缩算法有SPIHT和JPEG2000，而JPEG2000因具备高倍压缩率、渐进式传输、压缩模式选择灵活、容错性优越等优点，被国际空间数据系统咨询委员会（CCSDS）推荐为星上首选图像压缩算法，正逐步成为国内外光学卫星优先选用的算法。我国的“遥感六号”、“高分一号”[10]、法国pleiades等卫星均采用了该压缩算法。

本文以JPEG2000压缩算法为例，讨论图像压缩对相对辐射校正的影响，并分析均匀场区域易于产生残余条纹的机理。压缩和解压程序来自于OpenJPEG网站[11]。

1 条带残余成因的傅里叶分析

傅里叶变换是图像处理和分析的一种很重要的数学方法，通过离散傅里叶变换，将图像空间域变换到频率域，频率域图像能够很直观地反应图像的信息分布，而残余条纹是一种竖向的信号，在频率域图像中特征明显。

假设影像信息无任何损失，在地面处理过程中，相对辐射校正线性模型可表达为

式中 a、c是相对辐射校正参数；Gr表示经过了辐射校正后的图像（理想情况下的原始图像信号）；Gt表示校正前的图像。可知，星上图像生成过程的反向模型也是线性模型，即

若将式（2）看成信号系统，Gr是原始图像信号，由于传感器响应不一致性，输出的图像Gt包含条纹，后文中分别将Gr和Gt称作原图像和输出图像。k和b分别是乘性信号和加性信号，为简化问题，对加信号和乘信号的情况分开讨论。

（1）加性信号

加性信号的模型可表示为

光学卫星成像信号传递的过程如图1所示，卫星在数据下传之前，首先对输出图像进行压缩，传输到地面后解压，再由相对辐射校正参数还原为原图像。在数据压缩过程中，Gt可能损失信号，设有信号损失的原始输出图像为Gt′，设无信息损失的加性信号为b，图像恢复的过程可表示为

由于b分量也存在信息损失，设信息损失后的结果为b′，那么，式（4）将无法还原图像Gr，而是包含残余条纹和信息损失的图像Gr′，而b′–b就是相对辐射校正残余条纹的理论解释。

对式（3）的左右两边进行傅里叶变换，可得到输出图像Gt的频率域图像F（Gt）

式中 F（Gr）是图像Gr的频率域图像，与图像包含的地物相关；F（b）是条纹信号的频率域图像，是探元响应不一致的分量。在地物纹理较少且细节不丰富的区域，F（Gt）的高频部分主要分量是F（b），数据压缩过程中b分量的信号损失较多，就容易形成明显的残余条纹，这就是均匀场区域易出现残余条纹的重要原因。

（2）乘性信号

乘性噪声模型可表示为

直接对式（6）进行傅里叶分析比较困难，将其变换为

（k–1）Gr可看成与 b类似的加性信号，可推测乘性信号与加性噪声结论类似，区别在于：加性噪声与图像灰度均值大小无关，但乘性噪声对亮场可能更敏感。

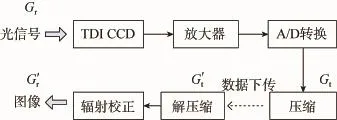
图1 光学卫星成像信号传递过程Fig.1 Signal transmission process of optical remote sensing satellite

2 模拟实验

为验证上一章傅里叶理论分析的结论，本文通过模拟卫星载荷数据获取的“摄影——压缩——下传——解压——去条纹”过程，再通过对残余条纹和图像信息损失的量化，将不同样本和压缩比实验的结果对比和分析来验证该结论。

2.1过程模拟

图像由数码单反相机摄影获得，后将图像重采样为1 824行、1 216列，位深8bit，灰度均值约为100。辐射校正模拟参数k和b由Matlab正态分布随机数生成器获得，其中k均值1.16、方差0.04，b均值16、方差4。

样本图像如图2所示，分别模拟光学遥感卫星图像包含地物的典型情形：样本A包括墙壁、裸露土地、水泥地等，模拟陆地表面的普遍情形，其中水泥地可视为均匀场，与水域覆盖的情形类似；样本B左半部分为水泥地（均匀场），与海边类似，右半部分纹理丰富；样本 C全部是碎石地，整幅图像纹理都很丰富，与荒漠戈壁地貌类似；样本D主要部分是白色墙壁，与海洋类似。

实验中先对样本图像加入模拟条纹，然后采用不同的压缩比压缩后再解压，最后利用k和b参数去除模拟条纹。

2.2 均匀场的残余条纹现象

将样本A用压缩比1∶3、1∶4和1∶6分别实验（如图3所示），目视对比可知，在均匀场区域残余条纹随着压缩比的增大而逐步变得明显，而周围非均匀场区域条纹不明显，这印证了前边所指出的图像均匀场区域易出现残余条纹的结论。

图2 样本图像Fig.2 Sample images

图3 不同压缩比的均匀场残余条纹现象Fig.3 Residual streaks phenomenon at various compression ratios

图3的对比结果说明：在图像压缩比过大的情况下，相对辐射校正难以取得理想的效果。进一步分析该问题，需要对残余条纹现象进行量化分析。

2.3 条纹与图像信息损失的量化

经过相对辐射校正地面处理的图像Gr′（后文简称恢复图像）不仅有残余条纹现象，图像信息也有损失。将原图像和恢复图像求差值，再将差值放大10倍，最后将差值图像的均值平移到128（256灰度级的中值）后进行傅里叶变换，生成频率域图像M的过程表达式为：

式中 Gr为原图像；Gr′为恢复图像。实验采用的压缩比为1∶6，频率域图像如图4所示。

图4 原图像和恢复图像差值的频率域图像Fig.4 Frequency domain image

差值包含两个分量，一是条纹信号的损失，二是图像信号的损失。残余条纹是竖向信号，故在图4中可观察到中部的亮线，亮线的灰度值是残余条纹强度的测度，亮线上的位置代表频率，从亮线的两段到中点代表从高频到低频。由于图像信息损失没有明显的规律，那么除无损压缩的情况外，在中间亮线以外的区域，图像的灰度值应大于零。通过对频率域图像中残余条纹信号和图像损失信号对应的区域进行灰度值取样，可定量比较分析残余条纹现象和图像信息损失。

设频率域图像M的p行和q列的灰度值为Mp,q。由于频率域图像左右对称的特性，只需取样亮线的左半部分，亮线位于图像正中间的一行，但有一定的宽度，故对亮线上下各延拓各一行，取每一列的最大灰度值，得到数组 in，n是频率域图像的列号。设图像频率域高和宽分别为h和w，n的取值从0到w/2，则in表示为

同理，对图像除亮线以外的其他区域取样可评价图像信号损失：对亮线周围，上下90像素的区域的每列影像灰度值取平均，得到数组ln

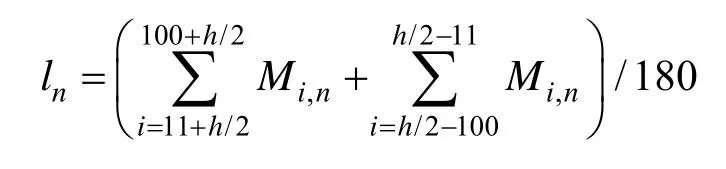
in和 ln可看成是残余条纹信号和图像信息损失关于图像信息频率的函数，n的值从小到大，代表图像信息高频分量部分到低频分量部分。由于in和ln波动较大，不便于分析比较，对in和ln分组，每组45个元素取均值得到新数组Im和Lm，本文分别定义为残余条纹和图像信息损失的测度：

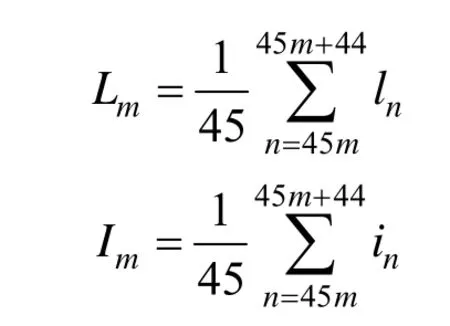
Im和Lm数值的变化更平缓，值的大小没有直接的物理意义，但其相对大小能够反映信号在不同频率区间的强弱关系；m是数组下标，其值代表不同频率区间的编号，编号从小到大，代表从高频到低频。

3 对比实验与分析

3.1 不同样本的对比

采用1∶6压缩，对所有样本分别模拟压缩与解压缩实验。残余条纹和图像信号损失测度曲线如图5、6所示。

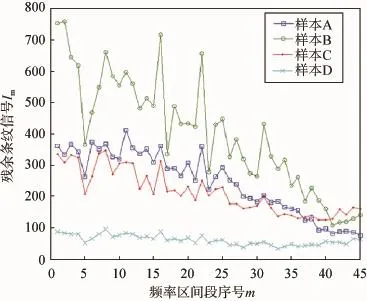
图5 残余条纹信号曲线ImFig.5 Signal of residual streaks

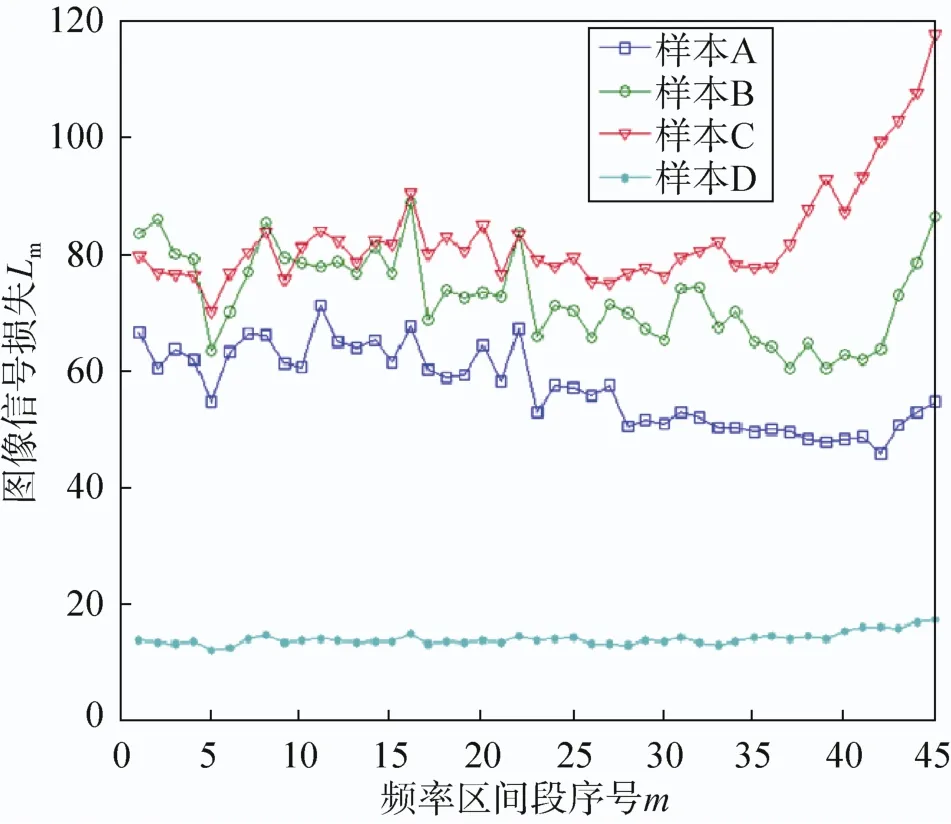
图6 图像信号损失曲线LmFig.6 Signal of image depression

由图5、6可知，不同样本条纹信号和图像信号损失表现不相同，原因是：根据压缩算法特性，图像采用1∶N压缩后的数据量为原始影像1/N，不同影像的信息量不同，那么压缩后信息损失量不同；而条纹信号的损失量（即残余条纹），还取决于原图像信号和条纹信号强度的比例。

样本D图像纹理少，信息量很小，压缩后条纹信号损失和原图像质量损失都不大，故残余条纹最小；样本C图像全部被纹理丰富地物覆盖，原图像的信号强度明显强于条纹信号，在图像压缩过程中，由于信息损失的主要成分是原图像信息的损失，原图像信息损失最多，但残余条纹强度却低于样本A和B；样本B的右半部分，信息丰富，但左半部分的水泥地是均匀场地物，图像压缩过程中条纹信号损失较多，故图像B的残余条纹现象最明显。

模拟影像的情形可在实际光学遥感卫星数据中找到例证。例如，在陆地地区影像中，湖面、旱地等均匀场地物区域容易出现残余条纹（样本 A或 B），但地物细节丰富的区域却没有条纹。在全部为水面的影像中，图像却没有明显条纹（样本D），但在海边地区水域的条纹又非常明显（样本B）。

3.2不同压缩比的对比

样本A包括不同细节丰富程度的地物，接近遥感卫星图像普遍情形，故采用样本A实验。对样本A分别采用无损、1∶2、1∶3、1∶4、1∶5、1∶6、1∶8和1∶10压缩比进行模拟压缩与解压实验，其中，1∶2至1∶8是各遥感卫星所采用的典型压缩比，1∶10用于对比，实验得到的测度曲线如图7所示。

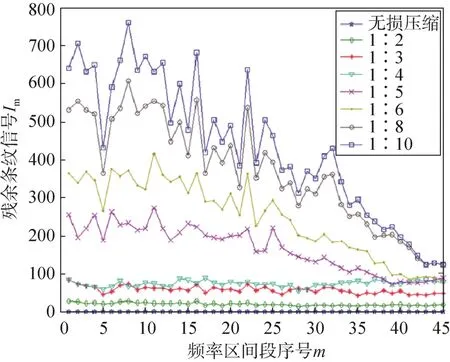
图7 不同压缩比的残余条纹Fig.7 Signal of residual streaks at various compression ratios

由图7可知，除无损压缩的Im与横轴几乎重合外，采用其他压缩比Im值都不为0。由此可知，在有损压缩的情况下，残余条纹现象无法避免。

3.3减少条纹信息强度的对比

设条纹信号削弱的倍数为z，取值分别为1、10、20、30、40、50。条纹信号削弱后，乘性条纹信号kw和加性条纹信号bw与削弱前的乘性信号k和加性信号b的关系表达式为：

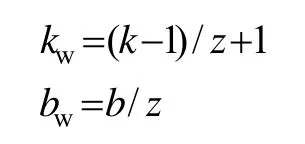
对不同条纹信号强度的情形分别实验，压缩比固定为1∶6，残余条纹信号强度的对比和图像信息损失的测度曲线对比如图8、9所示。

图8 残余条纹强度与条纹信号强度的关系Fig.8 Signal of residual streaks after streaks weaken

图9 图像信号损失与条纹信号强度的关系Fig.9 Signal of image depression after streaks weaken

由图8、9可知，随着条纹信号的削弱，残余条纹和图像信号损失都在减小，即残余条纹减小的同时，图像品质也在提高。随着条纹信号的削弱，Lm值趋近于一条渐进的曲线，这条曲线反映的是无响应不一致条纹的理想图像在压缩后的信息损失，由图8可知，对样本A，当条纹信号被削弱到1/40时（响应不一致性小于0.25%），残余条纹现象可忽略不计。

3.4 结果分析

3.2节和3.3节分别对比了在不同压缩比和不同条纹信号强度下残余条纹和图像信息损失的变化，可得到如下结论：

1）只要有损压缩，减少压缩比不能从根本解决辐射残余条纹问题，相对辐射校正残余条纹现象无法避免。

2）对一定的压缩比，当条纹信号下降到一定程度时，辐射残余条纹现象可能完全消失，图像品质也会随着条纹信号的减弱而提高。

从信息传输理论的角度可解释为：辐射响应不一致的条纹信号本是无用的噪声信号，若随着图像信号下传，必然会挤占星地传输带宽；若能减少条纹信号的强度，不但能抑制残余条纹现象，图像品质也能得到改善，等效提高了星地数传效率。

4 解决辐射残余条纹的方法

要彻底避免残余条纹现象只能采用无损压缩，但这将极大增加星地数传的压力。在传输带宽有限的前提下，星地数传不可避免地采用有损压缩。解决有损压缩产生残余条纹问题，理论上有两种方案可供选择：

1）根据信息不完整的输出图像恢复丢失的条纹信号，然后还原被压缩后的图像。由于信息已经丢失，这可能无法实现，即使理论上存在可能性，前提需对图像压缩器和解压器的实现细节和信号损失的规律进行深入研究。

2）在图像压缩前，尽可能的削弱响应不一致性条纹。受硬件制造工艺的限制，感光探元的响应不一致性很难进一步降低。文献[12]中星上相对辐射校正方案就是一种在图像压缩前削弱条纹噪声的方法：将地面定标结果上传到星上，在图像压缩前通过相对辐射校正削弱条纹信号（过程如图10所示），不但有可能彻底解决残余条纹问题，还能提高数据传输效率，改善图像的品质。

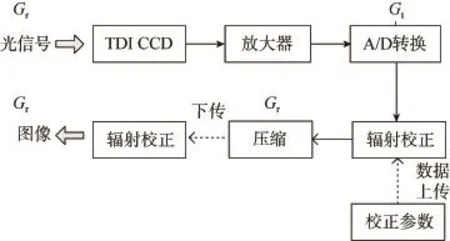
图10 星上相对辐射校正Fig.10 On-satellite relative radiometric calibration

5 结束语

本文从傅里叶分析的角度对图像压缩造成残余条纹现象的成因进行了深入的分析，以JPEG2000算法为例，分析了图像压缩对相对辐射校正的负面影响。模拟实验结果表明：图像有损压缩是相对辐射校正残余条纹现象产生的重要原因；在压缩比过大的情况下，相对辐射校正无法取得满意效果；在星地传输带宽有限而不得不采用有损压缩的前提下，降低图像压缩比不能彻底避免残余条纹现象的发生，而实施星上相对辐射校正不但有可能彻底解决相对辐射校正残余条纹问题，还将提升图像的品质，同时提高星地传输效率。

References)

[1]周胜利. 积分球在实验室内用于空间遥感器的辐射定标[J]. 航天返回与遥感, 1998, 19(1): 29-34. ZHOU Shengli. Radiometric Calibration Sphere in the Laboratory for Space Remote Sensor[J]. Spacecraft Recovery & Remote Sensing, 1998, 19(1): 29-34. (in Chinese)

[2]何红艳, 王小勇, 宗云花. CBERS-02B卫星TDICCD 相机的相对辐射定标方法及结果[J]. 航天返回与遥感, 2010, 34(4): 38-44. HE Hongyan, WANG Xiaoyong, ZONG Yunhua. Relative Radiant Calibration Method and Result of TDICCD Camera of CBERS-02B Satellite[J]. Spacecraft Recovery & Remote Sensing, 2010, 34(4): 38-44. ( in Chinese)

[3]王小燕, 龙小详. 资源一号02B星相机相对辐射校正方法分析[J]. 航天返回与遥感, 2008, 29(2): 29-34. WANG Xiaoyan, LONG Xiaoxiang. Analysis of Relative Radiometric Correction Method of CBERS-02B Camera[J]. Spacecraft Recovery & Remote Sensing, 2008, 29(2): 29-34. (in Chinese)

[4] DUAN Yini, ZHANG Lifu, YAN Lei. Relative Radiometric Correction Methods for Remote Sensing Images and Their Applicability Analysis[J]. Journal of Remote Sensing, 2014, 18(3): 597-617.

[5]郭建宁, 于晋, 曾汤, 等. CBERS-01/02卫星CCD图像相对辐射校正研究[J]. 中国科学, 2005, 35(增刊I): 11-25.GUO Jianning, YU Jin, ZENG Tang, et al. CBERS-01/02 Satellite Relative Radiometric Correction of CCD Image[J]. Science of China, 2005, 35(Supplement I): 11-25. (in Chinese)

[6]高正清, 杨志高, 王险峰. 相对辐射定标与相对辐射校正场[J]. 遥感与航空摄影, 2009(4): 48-53. GAO Zhengqing, YANG Zhigao, WANG Xianfeng. Relative Radiometric Calibration and Radiometric Calibration Site[J]. Remote Sensing and Aerial Photography, 2009(4): 48-53. (in Chinese)

[7]潘志强, 顾行发, 刘国栋, 等. 基于探元直方图匹配的CBERS-01星CCD数据相对辐射校正方法[J]. 武汉大学学报（信息科学版）, 2005, 30(10): 925-927. PAN Zhiqiang, GU Xingfa, LIU Guodong, et al. Relative Radiometric Correction of CBERS-01 CCD Image Based on Histogram-match[J]. Geomatics and Information Science of Wuhan University, 2005, 30(10): 925-927. (in Chinese)

[8] ADAMS M D. The JPEG-2000 Still Image Compression Standard[S]. Canada Dept. of Electrical and Computer Engineering University of Victoria, 2002-12-25.

[9]孙承志. 遥感影像压缩失真度量研究及应用[D]. 武汉: 武汉大学, 2010: 8-15. SUN Chengzhi. Distortion Measurement for Compressed Remote Sensing Images and Its Application[D]. Wuhan: Wuhan University, 2010: 8-15. (in Chinese)

[10]白照广. 高分一号卫星的技术特点[J]. 中国航天, 2013(8): 5-9. BAI Zhaoguang. The Technical Characteristics of Gaofeng-1 Satellite[J]. China Aerospace, 2013(8): 5-9. (in Chinese)

[11]Open JPEG Homepage[EB/OL]. [2014-3-1]. http://www.openjpeg.org/.

[12]武星星, 刘金国. 大视场多光谱空间相机在轨自动相对辐射校正研究[J]. 仪器仪表学报, 2013, 1(34): 104-111. WU Xingxing, LIU Jinguo. Research on on-orbit Automatic Relative Radiometric Correction of Multi-spectral Space Camera with Large Field of View[J]. Chinese Journal of Scientific Instrument, 2013, 1(34): 104-111. (in Chinese)

[13]肖学敏. JPEG2000卫星图像压缩方法的研究与实现[D]. 长沙: 国防科技大学, 2007: 2-3. XIAO XueMin. Research and Implementation of JPEG2000 Satellite Image Compression[D]. Changsha: National University of Defense Technology, 2007: 2-3. (in Chinese)

[14]张保贵. 空间CCD相机辐射校正算法分析[J]. 航天返回与遥感, 2014, 2(35): 91-96. ZHANG Baogui. Analysis of Relative Radiometric Calibration Algorithm of Space CCD Camera[J]. Spacecraft Recovery & Remote Sensing, 2014, 2(35): 91-96 . (in Chinese)

[15]叶培建. 线阵CCD器件主要性能参数及测试方法[J]. 中国空间科学技术, 1997, 6(3): 44-50. YE Peijian. Main Performance Parameters of Linear Array CCD Device and Testing Method[J]. Chinese Space Science and Technology, 1997, 6(3): 44-50. (in Chinese)

[16]王海燕, 于晋, 李照洲. 星载红外相机相对定标算法研究[J]. 航天返回与遥感, 2008, 30(6): 44-49. WANG Haiyan, YU Jin, LI Zhaozhou. Analysis of Relative Calibration Algorithm of Space-borne Infrared Camera[J]. Spacecraft Recovery & Remote Sensing, 2008, 30(6): 44-49. (in Chinese)

[17]周春城, 李传荣, 胡坚, 等. 基于行频变化的航空高光谱成像仪相对辐射校正方法研究[J]. 遥感技术与应用, 2012, 27(1): 33-38. ZHOU Chunchen, LI Chuanrong, HU Jian, et al. A Study on Passive Radiometric Correction Method based on Line Frequency Difference for Airborne Hyperspectral Imagery[J]. Remote Sensing Technology and Application, 2012, 27(1): 33-38. (in Chinese)

[18]湧曾 , 王文宇, 王静巧. 基于实验室定标和均匀景统计的相对辐射定标方法[J]. 航天返回与遥感, 2012, 33(4): 19-24. ZENG Yong, WANG Wenyu, WANG Jingqiao. A Method of Relative Radiometric Calibration Based on Laboratory Calibration and Homogeneous Scenes[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(4): 19-24. (in Chinese)

Analysis of Residual Streaks Based on JPEG2000 Compression Simulation

ZHENG Ke LIAO Yaoting HU Zhenlong

（Tianhui Satellite Center of China, Beijing 102102, China）

The results of relative radiometric correction of some domestic optical remote sensing satellite images are not so ideal that residual streaks exist. In the case of JPEG2000 compression, this article analyses negative impact of image compression on relative radiometric correction. Firstly, this phenomenon is analysed by Fourier analysis. Then a compress-decompress simulation experiment proves the conclusions of the Fourier analysis: when image compression ratio is too large, relative radiometric calibration is difficult to achieve satisfactory results, and residual streaks phenomena may arise. Finally, based on measurement of signal of residual streaks and image depress, a comparative analysis confirms that lower image compression ratio does not fundamentally solve the problem of residual streaks, but on-satellite radiometric correction before image compression is a better solution to suppress residual streaks.

image compression; compression ratio; on-satellite radiometric correction; relative radiometric correction; space remote sensing

TP79

: A

: 1009-8518(2016)01-0080-09

10.3969/j.issn.1009-8518.2016.01.010

郑柯，男，1987年出生，2013年毕业于武汉大学测绘遥感信息工程国家重点实验室，获数字摄影测量专业硕士学位。工程师，研究方向为在轨几何定标和在轨辐射定标。E-mail：452788431@qq.com。

（编辑：夏淑密）

2015-04-12