一种模板匹配的快速实现方法

李超 于飞 康晓军

（北京空间机电研究所，北京 100094）

一种模板匹配的快速实现方法

李超 于飞 康晓军

（北京空间机电研究所，北京 100094）

文章主要研究视频图像运动中目标轨迹的准确预测和快速定位，从而能够为光电跟踪控制系统提供可靠的位置数据和运动参数。光电跟踪控制系统要求对运动目标有较快的响应速度，响应时间越短，系统的实时性就越好，因此快速而准确的目标跟踪算法显得尤为重要。高帧频的跟踪控制系统限制了图像处理的计算时间，实时性与计算精度很难兼顾，传统的目标跟踪方法难以适用。针对这一问题，文章提出基于Kalman滤波轨迹预测的模板匹配方法，通过建立目标的运动模型，给出了Kalman滤波的过程方程与测量方程。在目标跟踪过程中，对当前帧匹配得到的目标运动数据进行滤波处理，预测下一帧目标的运动参数。文章方法的优点是可以利用匹配值不断地修正预测值，同时修正系统模型参数和噪声统计参数，保证计算的快速性与跟踪的准确性。文章方法的优势在于摒弃了遍历搜索目标的盲目性，使目标跟踪更具有针对性，在保证精度的同时节省了时间。通过多次运动测试，仿真结果表明：算法具有良好的实时性和一定的适应环境变化的能力。

目标跟踪 模板匹配 卡尔曼滤波 卡尔曼预测

0 引言

在跟踪技术领域，光电跟踪控制系统是涉及多项关键技术的复杂系统工程，主要对高速摄像机拍摄的序列图像目标进行实时跟踪。目标跟踪算法[1]近几年发展十分迅速，而模板匹配算法具有不完全依赖图像分割效果的特点，并且对场景图像品质要求不高，可在低信噪比条件下稳定工作。模板匹配算法在成像跟踪中有着重要地位，但是现有模板匹配算法运算量大，计算速度在现有技术条件下受到制约，导致匹配速度无法达到实时性的要求，因此无法应用于光电跟踪控制系统中。如何兼顾计算速度与精度的要求，一直是国内外研究学者思考的问题[2-8]。

很多方法如FFT相关算法、序贯相似性检测算法、变分辨率相关算法等大多存在着适用范围窄、精度低、速度提高不明显等缺点，无法满足工程实际要求。本文介绍一种利用 Kalman滤波器的预测与修正两种功能对模板匹配算法进行优化，使算法更有针对性和有效性，以减少计算量、提高匹配速度为目的进行改进，建立了适当的数学模型。基于Kalman滤波给出相应的滤波方程，根据前一时刻Kalman滤波得到的目标修正位置信息，采用 Kalman一步预测算法估计目标在当前时刻的可能位置，以预测的位置为中心，搜索范围匹配确定目标在当前图像中的准确位置，仿真结果表明，本文所采取的方法能够缩小目标搜索范围，减小计算量，提高目标跟踪精度。

1 模板匹配

基于匹配的目标跟踪方法的依据为图像灰度互相关准则。常用的匹配方法如基于特征点的匹配，其要求被跟踪目标明确或具有某类特征[9]，基于模板匹配的方法注重模板图像的相关性，对目标没有限定，故本文选用模板匹配实现运动目标跟踪。模板的选取基于人机交互，操作员选取视频图像中一定区域作为目标模板，跟踪目标过程由计算机自动实时处理作为支持[10]。在运动目标跟踪的过程中，将已知的目标模板与待匹配子图像进行匹配，在视频图像中通过计算目标模板与待匹配子图像的互相关值。如图1所示，整个区域为待匹配子图像，M与N为模板图像的列与行，(m,n)是当前匹配位置，t(i,j)是模板图像上的第i行和第j列的像素的灰度值。选择具有最大互相关值的当前匹配位置作为目标在当前帧图像中的实际位置，从而实现运动目标的跟踪定位[11]。

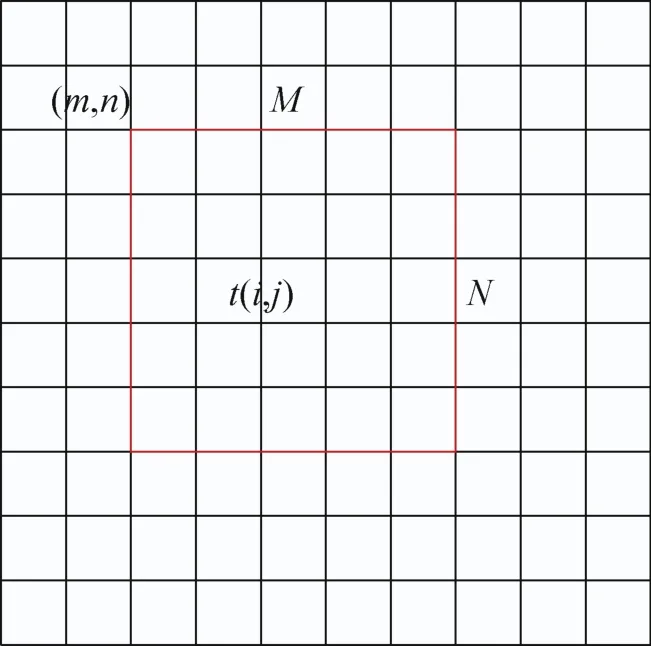
图1 模板匹配示意图Fig.1 Sketch map of template matching

1.1 互相关计算优化

模板匹配算法的核心就是在序列图像内搜索与所选模板最相似的匹配位置，本文研究的匹配准则为归一化积相关(NPROD)匹配准则，为了尽可能降低噪声对匹配结果的影响，采用去均值归一化积相关(NNPROD)匹配准则[12]。互相关运算公式如下：

式中 目标模板大小为M×N； R( m, n)表示目标模板与待匹配子图像在(m, n)点上的互相关值，且满足0 ≤ R( m, n )≤1；f( i+ m, j+ n)表示的是待匹配子图像中第i+m行与第 j+n列交叉点的像素的灰度值；t( i, j)是模板图像上的第i行与第j列交叉点的像素的灰度值；表示的是目标模板灰度值的平均值；表示的是待匹配子图像实时子区间灰度值的平均值，其计算方法为：

随着目标模板大小的增加，上述算法的计算量成倍增加。为了解决上述问题，需要针对算法进行优化，提出合理的减小计算量的算法。

因为相似度匹配含卷积运算，故而可采用快速傅里叶变换进行简化计算。而NPROD算法实际上是将待匹配子图像与目标模板的灰度值按矢量计算，求两者夹角的余弦值。只有当矢量相等时，互相关值才有等于1的情况，因此NPROD算法不受乘性灰度误差影响，但对于加性误差却非常敏感。而NNPROD算法不仅不受乘性灰度误差影响，而且可以抑制加性误差的影响，这也是本文采用NNPROD的主要原因。

光电跟踪控制系统的实时性很强，建议搜索窗不能开的太大。这就导致搜索窗内图像与参考模板图像的相似度很接近，这样相关系数值比较大，匹配点周围的相关系数值比较接近，不容易得到真正的匹配点。为了放大相关系数值的差别，本文把公式（1）的分母去掉，变成：

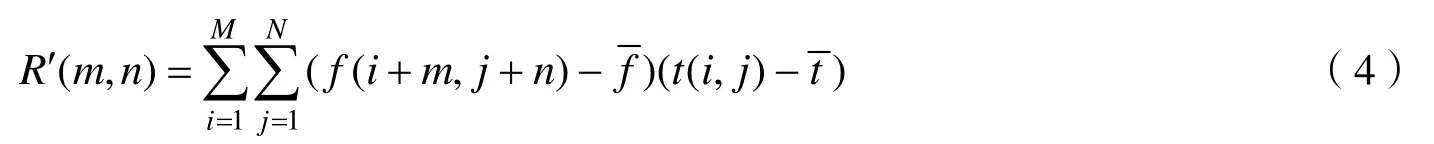
将公式（2）、（3）代入公式（4）式展开得到：

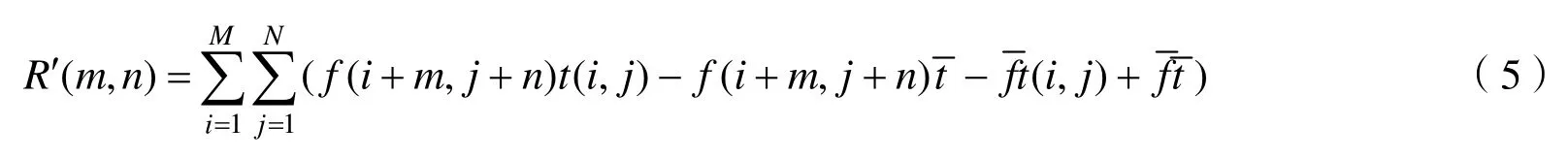
为了简化处理，本文认为图像灰度值满足均匀分布，用均值代替各个点像素值，可以得到近似关系：

将公式（6）带入公式（5）化简得到：

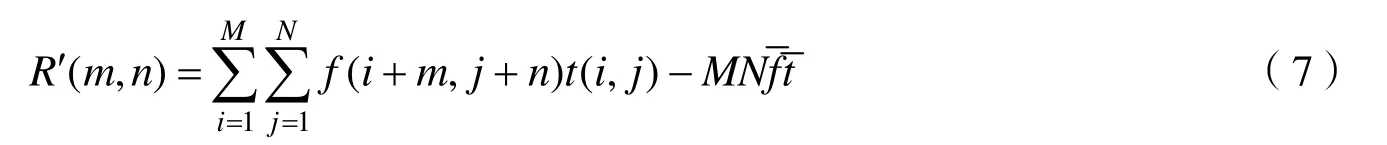
公式（7）称之为快速NNPROD匹配准则。

1.2 计算量分析

在同样大小M×N像素的模板，对公式（1）与公式（7）匹配运算比较，NNPROD互相关计算量与快速NNPROD互相关计算量如表1所示：

表1 计算量对比Tab.1 Comparison of calculation between NNPROD and fast NNPROD

由表1数据可以得到，快速NNPROD较NNPROD而言，总的计算次数约为NNPROD算法的1/4，提高了的匹配速度。上述快速 NNPROD用于模板匹配算法的准则。在图像匹配跟踪过程中，目标模板在当前帧待匹配子图像内滑动，并与待匹配子图像作如公式（7）的互相关运算， R＇( m, n)的最大值对应的当前匹配位置作为最佳的匹配点。

2 Kalman滤波器设计

实现快速模板匹配的主要入手方向有如下两点：

1）减少每次模板互相关运算的计算量；

2）优化搜索策略，减少搜索像素点数。

在已经对模板匹配的计算量做出优化后，接下来是考虑如何优化搜索策略。本文采用预测跟踪处理技术[13-16]，根据目标之前的位置信息和运动状态，估计出目标下一步可能的位置，可以实现在相对较小的区域内进行匹配运算，大大降低了寻找目标的时间。

2.1 轨迹线性预测算法

假设相邻帧间图像相似度大，位置变化小，可近似认为目标做直线运动，即系统观测方程满足线性。假设噪声满足高斯分布，则可以采用线性Kalman预测方法实现对运动目标的轨迹预测。

Kalman滤波是一种线性最优滤波算法，滤波准则是均方误差最小。把图像处理技术与Kalman滤波算法结合起来[17]，利用 Kalman滤波的最优估计结果预测目标运动状态，从而预测目标运动轨迹，系统的状态方程和观测方程为：

式中 xk是k时刻的状态向量；xk-1为k-1时刻的状态向量；A是状态转移矩阵；B为控制矩阵；uk-1为控制量，由于本文跟踪系统没有控制量即uk-1=0；zk为观测向量；H是观测矩阵；wk-1和γk是相互独立的高斯白噪声。

Kalman滤波器的系统状态预测方程：

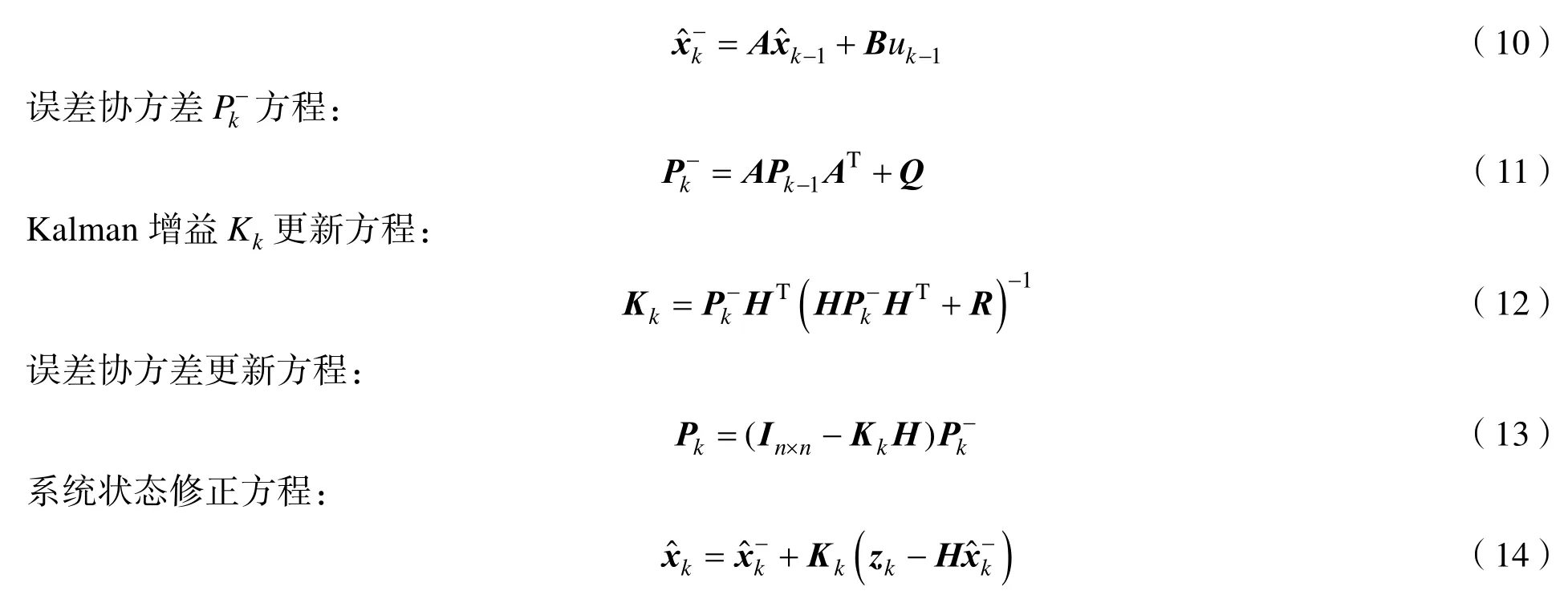
2.2建立目标运动模型

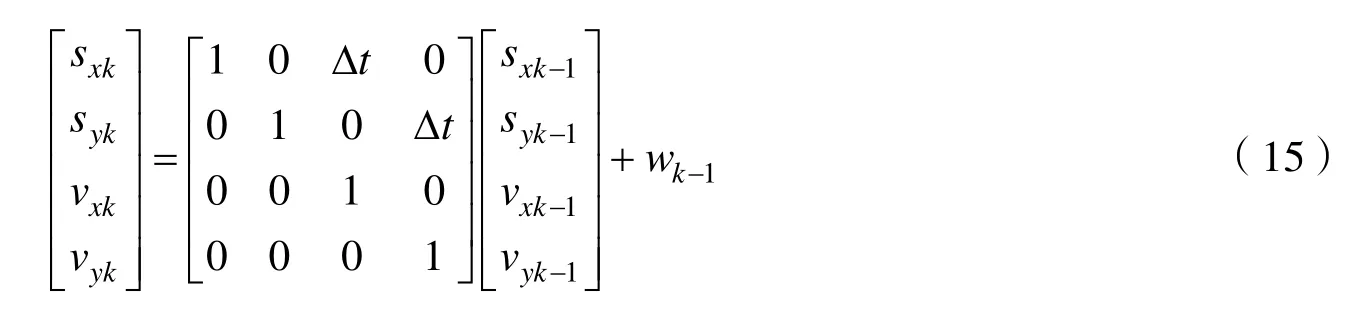
式中 Δt为帧频的倒数。

为了修正目标状态参数，进行目标信息的准确估计，本文的观测向量是包含位置与速度信息的4维向量，速度修正一方面使位置信息更为准确，另一方面为目标搜索提供依据。

2.3 运动目标搜索策略

模板匹配算法要从视频的每一帧图像中遍历搜索检测出目标位置，计算量很大。可以利用 Kalman滤波器，在 k-1时刻获得的修正目标信息基础上，对k时刻目标的信息进行预测。但是该预测值存在误差，所以在k时刻，以预测值为圆心，以目标尺寸L加时间段内目标的预计运动距离为半径，如图2所示，确定k时刻目标搜索范围Sk：

式中 vk为k时刻目标运动合速度，满足。

在k时刻，由Kalman 预测方程得到运动目标预测目标状态向量，得到目标的预测位置，在以预测位置为圆心，搜索范围Sk为半径的圆形区域内采用优化NNPROD的模板匹配算法寻找目标最优位置，重新计算速度信息，构成k时刻的观测向量zk，并将匹配得到的最优位置作为最终目标位置保存下来。

利用k时刻的观测向量zk与Kalman滤波器的修正方程，得到 k时刻的修正目标状态xk，用于k+1时刻目标状态向量的预测。

图2 搜索范围示意图Fig.2 Sketch map of searching area

3 仿真分析

为了验证本文提出的基于Kalman 滤波的模板匹配快速算法，进行了计算机Matlab仿真分析。应用处理器为Intel(R) Core(TM) i5-3470 PC机，在Matlab2008a软件平台进行仿真实验，得到NNPROD与快速NNROD的帧间计算时间比较如表2所示。

可以看出，在模板尺寸为30×30像素的情况下，NNPROD算法平均计算时间为0.07s，为14帧频，再考虑帧间数据传输与转换，计算时间是不能容忍的。快速NNPROD算法的平均计算时间为0.004s，为250帧频。对于高帧频跟踪有足够的计算时间余量。并且随着模板尺寸的增大，NNPROD算法平均计算时间迅速增大，在模板尺寸为100×100时，已经不到4帧频，而快速NNPROD算法随着模板增大，计算时间增量很小，仍可以用于高帧频光电跟踪控制系统中。

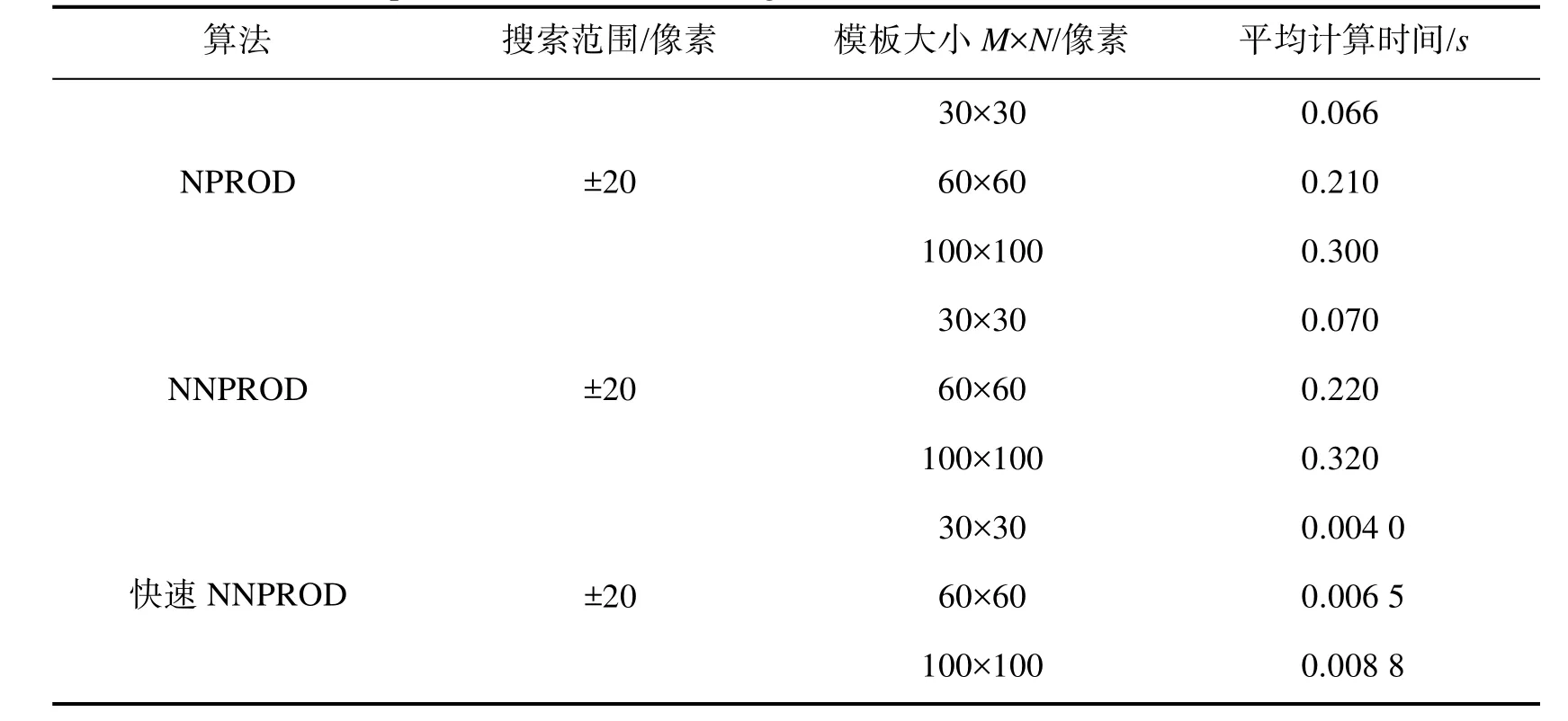
表2 不同算法与帧计算时间比较Tab. 2 Comparison of frame calculating time between NNPROD and fast NNPROD

在进行仿真时，假设系统的过程噪声、量测噪声均为零均值高斯白噪声，初始误差协方差矩阵取。如图3是目标跟踪的展示图，在含高斯噪声的背景下对目标进行跟踪试验，绿框代表了选取的目标模板，目标为绿框内的白色圆形。用目标模板的中心代表白色圆形的等效位置，初始位置为（100,47），近似匀速运动。如图4所示，采用线性Kalman 滤波的模板匹配算法得到目标运动的匹配轨迹与Kalman滤波器的预测轨迹。

用线性模型近似代替非线性运动模型，用Kalman滤波器预测的位置必然存在误差，只要Kalman滤波器的修正结果在最终匹配位置附近，即可保证本算法在最快的时间内找到最终的位置。目标的运动速度大小存在±10%的随机变动，通过统计坐标数据计算匹配轨迹与预测轨迹的误差在±5个像素之内，认为相差5个像素之内的预测点为跟踪准确点，相差5个像素以上的预测点为跟踪漂移点，如表3所示，展示了本算法的跟踪性能。

图3 目标跟踪图像Fig. 3 Image of target tracking

图4 匹配轨迹与预测轨迹Fig. 4 Tracks of matching and Prediction

表3 目标跟踪性能分析Tab.3 Analysis of the target tracking performance

结合表2与表3的实验结果可以看出，在目标跟踪过程中，模板大小一定，运动形式一定时，本文采用基于Kalman 滤波的模板匹配算法确定的目标搜索范围，都能够包含目标，同时使得搜索范围缩小。模板匹配与 Kalman滤波预测相结合，对目标运动状态进行预测跟踪，将图像处理的范围缩小。本算法基于NNPROD，而与NNPROD相比，在保证精度的同时减少了计算时间。

4 结束语

本文采用基于Kalman 滤波的模板匹配算法确定视频图像中目标的运动轨迹，避免对全帧图像的遍历搜索，减小了目标匹配的计算量，实现了一种“预测一匹配—修正—预测”的反馈形式。仿真结果表明，本文所采用的基于 Kalman滤波的模板匹配算法，能够有效减小目标跟踪时的计算量，具有较好的目标跟踪精度。

References)

[1]邵文坤, 黄爱民, 韦庆. 目标跟踪方法综述[J]. 影像技术, 2006(1): 271-275. SHAO Wenkun, HUANG Aimin, WEI Qing. Research on Object Tracking[J]. Image Technology, 2006(1): 271-275. (in Chinese)

[2] VRABEL M J. A Target-Tracking Algorithm[R]. Army Research Lab Adelphi MD, 2000.

[3] MARCHAND E, CHAUMETTE F. Feature Tracking for Visual Servoing Purposes[J]. Robotics and Autonomous Systems, 2005, 52(1): 53-70.

[4] LUO Xiaobo, FAN Hongqi, SONG Zhiyong, et al. Passive Target Tracking with Intermittent Measurement Based on Random Finite Set[J]. Journal of Central South University, 2014, (6): 2282-2291.

[5] SHI Xiaoping, WANG Yuzhe. Enhancement of Target Tracking Using Target Orientation Information[C]. The 25thChinese Control and Decision Conference, Gui Yang, Chinese Society of Aeronautics and Astronautics, 2013.

[6]陈沈轶, 钱徽, 吴铮, 等. 模板图像匹配中互相关的一种快速算法[J]. 传感技术学报, 2007, 20(6): 1326-1327. CHEN Shenyi, QIAN Hui, WU Zheng, et al. Fast Normalized Cross-Correlation for Template Matching[J]. Chinese Journal of Sensors and Actuators, 2007, 20(6): 1326-1327. (in Chinese)

[7] LOTSPEICH J T. Tracking Subpixel Targets with Critically Sampled Optical Sensors[R]. Naval Postgraduate School Monterey CA, 2012.

[8] WANG Huilin, WANG Ying, AN Ru, et al. Fast Image Matching Algorithm Based on Key Points[C]. Remote Sensing of the Environment: 18th National Symposium on Remote Sensing of China. Wuhan: Nanjing University, 2014.

[9]耿蕾蕾, 林军, 龙小祥, 等. “资源三号”卫星图像影像特征匹配方法研究[J]. 航天返回与遥感, 2012, 33(3): 94-96. GENG Leilei, LIN Jun, LONG Xiaoxiang, et al. Research on Feature Matching Algorithm for ZY-3 Image[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(3): 94-96. (in Chinese)

[10]杨文, 孙洪, 曹永锋. 合成孔径雷达图像目标识别问题研究[J]. 航天返回与遥感, 2004, 25(1): 39-41. YANG Wen, SUN Hong, CAO Yongfeng. Study on Automatic Target Recognition in SAR Imagery[J]. Spacecraft Recovery & Remote Sensing, 2004, 25(1): 39-41. (in Chinese)

[11]陈翔, 陈鹏. 基于改进模板匹配的模板跟踪算法[J]. 计算机应用, 2011, 31(z2): 127-128. CHEN Xiang, CHEN Peng. Object Tracking Algorithm Based on Improved Template Matching[J]. Journal of ComputerApplications, 2011, 31(z2): 127-128. (in Chinese)

[12]ZHUO Yang. Fast Template Matching Based on Normalized Cross Correlation With Centroid Bounding[C]. International Conference on Measuring Technology and Mechatronics Automation. Changsha: Institutes of Technology of Changsha & Central South University, 2010.

[13]仝晓龙, 窦腾飞, 刘艳红. 运动目标跟踪技术综述[J]. 科技创新与应, 2014, (18): 18-19. TONG Xiaolong, DOU Tengfei, LIU Yanhong. Survey of Moving Target Tracking Technology[J]. Technology Innovation and Application, 2014, (18): 18-19. (in Chinese)

[14]ZHAO Xiafu, YAN Han. Centroid Weighted Kalman Filter for Visual Object Tracking[J]. Measurement, 2012, 45(4): 650-655.

[15]TANG Xinhua, GIANLUCA F, EMANUELA F, et al. Theoretical Analysis and Turning Criteria of Kalman Filter-based Tracking Loop[J]. GPS Solutions, 2015, 19(3): 489-503.

[16]ABHARI S Q, ERSHADI T Z. Target Tracking Based on Mean Shift and KALMAN Filter with Kernel Histogram Filtering[J]. Computer and Information Science, 2011, 4(2): 152-160.

[17]谭菊. 基于Kalman滤波的目标轨迹预测[J]. 重庆文理学院学报, 2009, 28(5): 28-29. TAN Ju. Target Track Prediction Based on Kalman Filter[J]. Journal of Chongqing University of Arts and Sciences, 2009, 28(5): 28-29. (in Chinese)

[18]SINHA A, KIRUBARAJAN T, BAE-SHALORM Y. Application of the Kalman-Levy Filter for Tracking Maneuvering Targets[J]. 2007, 43(3): 1099-1107.

[19]赵其杰, 屠大维, 高健. 基于Kalman滤波的视觉预测模板跟踪及其应用[J]. 光学精密工程, 2008, 16(5): 937-941. ZHAO Qijie, TU Dawei, GAO Jian. Kalman Filter Based Vision Predicting and Object Tracking Method and its Application[J]. Optics and Precision Engineering, 2008, 16(5): 937-941. (in Chinese)

[20]陈少华, 闫钧华, 朱智超, 等. 基于 Kalman滤波和自适应模板的目标相关跟踪研究[J]. 电子设计工程, 2011, 19(23): 189-191. CHEN Shaohua, YAN Junhua, ZHU Zhichao, et al. Correlation-based Target Tracking Algorithm Based on Kalman Prediction and Adaptive Template[J]. Electronic Design Engineering, 2011, 19(23): 189-191. (in Chinese)

A Fast Method of Template Matching

LI Chao YU Fei KANG Xiaojun

（Beijing Institute of Mechanics & Electricity, Beijing 100094, China）

Accurate motion predicting and quick positioning of moving target in video images are mainly studied in this paper. In order to it is required that provide credible position data and motion parameters of target in electro-optical tracking control system, the electro-optical tracking and control system should have a faster response. The shorter the response time of the tracking system is, the better the real-time performance of the system is. Therefore, a fast and accurate algorithm of target tracking is very important. Aracking control system of high frame rate limits the computing time of image processing. It is difficult to take into real time and calculation cost account. The simultane-ously traditional target tracking methods are difficult to apply. To solve this problem, a template matching method based on Kalman filter is proposed in this paper. The target motion model is established, and the Kalman filtering process and measure equations are given. During tracking, the target motion data received in current frame are used in filtering processing and predicting the motion parameters of target in the next frame. This method can use matching value to modify the predicted values, the parameters of system model and statistics noise at the same time, which makes sure the speed of calculation and the accuracy of tracking. The advantages of this method are to abandon the blind searching for target, ensure the target tracking algorithm more individualized, make sure both accuracy of tracking and reduction of time.Through many test of moving target, the simulation results show that the novel algorithm has the cap ability of real time and adapting to changes of environment.

target tracking; template matching; Kalman filter; Kalman prediction

TP751

: A

: 1009-8518(2016)01-0063-08

10.3969/j.issn.1009-8518.2016.01.008

李超，男，1989年生，现在中国空间技术研究院光学工程专业攻读硕士学位。研究方向为精密光电仪器控制技术。E-mail：IhIc2992650@163.com。

（编辑：刘颖）

2015-07-19