给“确定位置”以不同的“位置”——“确定位置”同课异构教学思考

□郑莉

给“确定位置”以不同的“位置”
——“确定位置”同课异构教学思考

□郑莉

通过对“确定位置”一课不同设计的比较来探讨如何分析教材、研究学生、高效教学。通过“三比”（比导入：“从一维到二维，经历由模型组合形成方法的过程”VS“从活动到模型，经历由数学抽象形成方法的过程”；比操作:“回归现实，感悟规律，促进活动经验的数学化”VS“开放设问，激发想象，数形结合感悟数对规律”；比应用：“利用同一性实例，强化知识的内涵理解”VS“利用比较性实例，廓清知识应用的外延”）对“数形结合”的教学提出若干建议。

确定位置 同课异构 比较

在平面上确定位置的常用方法有两种：一是方向与距离法，如点B在点A的北偏东30°距离点A40千米处；还有一种就是有序数对法，在小学里，就是以点A为坐标原点，做第一象限，用数对表示点B相对于点A的位置。人教版六年级上册“确定位置”讲的是后一种情形。下面笔者尝试用两种不同的思路来设计这一内容，进行一次同课异构教学思考，以期在思维碰撞中获得更深层次的教学认识。

【教学尝试】

一、选择不同的情境，设计不同的导入方式

现实生活中常用的在直线上（一维空间）确定位置有两种情形：一是从前到后（或从后到前）的第几个，二是从左到右（或从右到左）的第几个。现实生活中常用的在平面上（二维空间）确定位置需要前后、左右两个要素。这就实现了从一维到二维的跨越，当然，不论几维空间确定位置，都要先确定参照点（原点）。

课伊始，选择怎样的情境导入尤为重要，我们设计了两种不同的思路。

思路一：从一维到二维，经历由模型组合形成方法的过程。

课一开始，教师出示一年级上册中的排队图（见图1），让学生回忆在一维空间情境下的顺序建立方式，回顾左右、前后等概念。然后出示教室里学生的座位图（见图2），让学生思考在二维空间情境下如何确定每一个人的位置——不仅需要左右，还需要前后，然后明确行和列的意义——左右为行、前后为列，讨论确定第一行和第一列，然后把行列抽象为线，学生抽象为纵横线的交点，实现由座位图到方格图的过渡。

图1

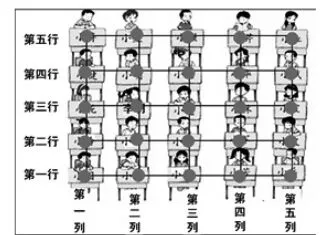
图2

当然，这样的设计也是我们为后续学习中实现从一维、二维过渡到三维空间确定位置的方法做了有序思考的蕴伏。

思路二：从活动到模型，经历由数学抽象形成方法的过程。

课一开始，教师直接出示座位图（见图3），请学生对号入座，在座位图中找出自己的位置，并说说是怎么找到自己的位置的。然后讨论在确定位置的过程中需要明确哪一些要素。根据这些要素，把座位图抽象为图4的方格图。

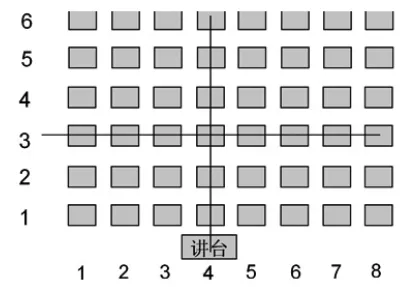
图3

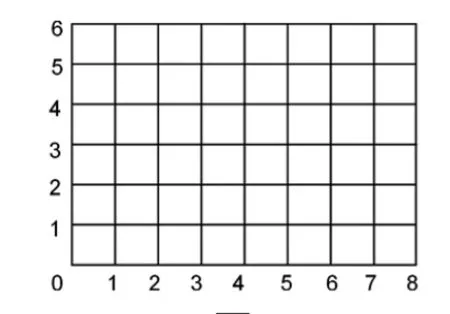
图4

思路一实际上是披着现实情境外衣的数学导入，把一维空间中确定位置的两种情形加以组合解决二维空间中确定位置的问题。思路二是实实在在地引入生活情境，直接把座位图抽象为方格图。

两种思路都有其数学价值，它们都呈现了一个知识动态生成的过程，帮助学生从感性认识提升到理性思考，实现具体形象思维到抽象逻辑思维的转变。

二、设计不同的操作，构建不同的学习形态

新知形成后，需要通过适当练习或操作性活动，感悟规律，进一步深化知识理解，发展学生的数学思维。如何达到这一目的呢？我们设计了显著分化的操作活动。

思路一：回归现实，感悟规律，促进活动经验的数学化。

教师引导学生将目光投向教室，请学生用数对表示自己所在的位置，并记录在草稿本上。请学生相互介绍自己和好朋友的位置。接着教师说数对，请符合要求的学生起立：（7，1）（7，2）（7，3）（7，4）（7，5）。进而引导学生思考：“奇怪，站起来的同学怎么正好是一列呢？表示这些同学的数对有什么特点？”引导学生发现数对中第一个数相同的，他们就在同一列。列数相同情况下数对中的一个数是确定的，一个数是在变化的。接着进一步引发思考：如果让你来出一些数对，你能让一列、一行或一排同学站起来吗？你能不能说一个数对，就把一列、一行或一排的同学都包含在里面？学生马上想到了用字母来表示，出现了（4，x）（5,x）（x，3）（x，x）（x，y）等各种不同的数对。教师继续追问：（x，x）可能是谁？当x等于1时，表示谁？当x等于2时，表示谁？究竟哪些同学才有可能？（x，y）呢？

这一设计始终围绕教室座位这一学生熟悉的现实情境，通过说、站、想的环节，帮助学生深刻认识数对的现实意义，积累丰富的感性经验。

思路二：开放设问，激发想象，数形结合感悟数对规律。

笛卡儿创造了坐标思想，用数对表示位置是这一思想的具体体现。在此基础上建立起了一个新的数学分支——解析几何，将数与形完美地统一起来，用代数的方法研究几何问题，是其最伟大的价值。这一设计试图进一步凸显数形结合，对解析的基本思想有所感悟。

教师在方格图中出示一条线段。让学生思考：如果在方格图中增加一个点，这个新增加的点与原有这条线段上的两个端点相连，可能会构成什么图形？学生猜想，增加一个点后，与原有的两个端点相连可以构成三角形，也可能构成线段。教师继续启发学生想象，在什么情况下，构成的图形是线段？在什么情况下是三角形？学生思考后发现，当第三个点的位置在原有的这条线段所在直线之外的任意一个地方，构成的图形是一个三角形。教师用课件呈现第三点在不同位置时，所构成的三角形的不同变化形态。如果第三个点的位置在原有的这条线段所在的直线上，则构成的图形仍然是线段。

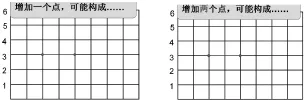
教师继续引导学生思考：如果在原有线段之外增加两个点（与原线段不在同一直线上），你猜想可能会构成什么图形？学生猜想可能是正方形、长方形、一般四边形、平行四边形、梯形等等。教师课件呈现构图的过程，请学生描述自己的猜想。

然后，教师组织学生将思维聚焦在：如果增加的两个点与原有线段构成一个正方形，你觉得有几种情况？并请学生用数对描述出点的位置。

最后，教师隐去方格图，让学生思考：在这条线段之外，增加两个点，构成正方形，没有了方格图的帮助，你还能用数对表示出这两个点的位置吗？有几种可能性？这些点有什么特点？

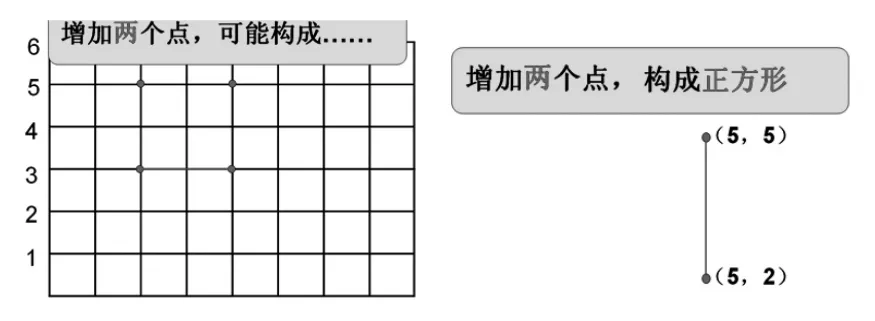
将数对运用到变化了的图形中，这个设计有一定的难度，对六年级的学生来说还是比较抽象的。

同样是规律，一个从生活到数学，一个从数学到数学。第一种思路更为细腻，起点低，步子小；第二种思路更为开放和整体，对学生的思维能力和教师的课堂驾驭能力提出了更高的要求。

三、引入不同的实例，构建不同的应用渠道

数学课中引入生活原型很常见，这节课也不例外。不过两节课的思路略有不同。

思路一：利用同一性实例，强化知识的内涵理解。

教师引导学生观察生活中的数对，出示国际象棋和中国地图，让学生解读。

学生认为国际象棋的棋盘，行用数字表示，列用字母表示，棋子走到哪一格就用相应的数字、字母表示，例如王后从2F走到5B，就表示王后从第2行第6列斜着走到第5行第2列，用这样的方法可以记录下棋的全过程，这种思想与数对表示位置的思想一致，因此，国际象棋的棋谱可以说是用特殊的数对记录的。

在中国地图上，北京所在的位置是东经116度23分，北纬39度54分。用这样的数对可以确定任何一个城市的位置。地球是球体的，是一个曲面，用这样的数对就可以在曲面上确定位置。

思路二：利用比较性实例，廓清知识应用的外延。

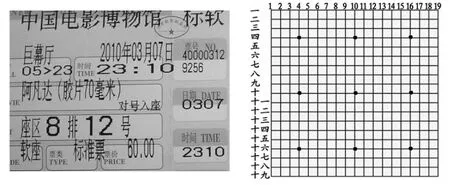
教师引导学生观察生活中表示位置的情况，并思考哪些是用数对来确定位置的。教师呈现的资料中，有用一个数来表示位置的，例如买票时小明排在队伍的第3个；也有用两个数表示位置的，如电影票上的8排12号，围棋棋盘中棋子的位置，等等。然后启发学生思考，以后我们还会学习哪些确定位置的方法呢？学生猜想，用3个数表示位置，如家庭住址2幢1单元301室；用方向和距离表示位置等等。

两种思路各有优势，针对性强便于技能巩固，拓展面宽便于意义理解，两个价值取向对于数学学习都是有益的，需要教师根据自己的想法去平衡和取舍。

【研究体会】

当我们将这两堂课进行对比之后，可以发现，在不同设计的背后蕴含了诸多相似的价值追求。关注知识本质、关注思维的发展是我们一致的价值导向。关注知识的不同侧面和学生学习的不同可能性形成了本课两种风格迥异的教学形式。一堂课是一种教学理解的体现，也是一种价值观的反映，我们用怎样的眼光来理解数学、看待学生的数学学习，我们就会用怎样的行动来体现这种思考。在与课堂的生成和学生的互动中，我们拥有了不断接近数学和教学本源的真实体验。提升我们的数学理解和教学能力，才能不断提升学生的思维层次，不断提高数学课堂教学的有效性。

[1]张丹.小学数学教学策略[M].北京：北京师范大学出版社，2010.

[2][荷]弗赖登塔尔.作为教育任务的数学[M].陈昌平，唐瑞芬，等，编译.上海：上海教育出版社，1995.

[3]李士锜，张晓霞，金成梁.小学数学教学案例研究[M].北京：高等教育出版社，2010.

（浙江省杭州市育才外国语学校 310012）