焦面拼接反射镜热稳定性对MTF的影响

李富强蔡伟军范俊杰



焦面拼接反射镜热稳定性对MTF的影响

李富强蔡伟军范俊杰

（北京空间机电研究所，北京 100094）

光学拼接是扩大航天相机视场的有效方法。焦平面采用光学拼接时，拼接反射镜的热稳定性对探测器的共线性和共面性有一定的影响，共线性和共面性误差会引起时间延迟积分电荷耦合器件（TDICCD）的光学调制传递函数（MTF）的下降。文章首先在三维欧式空间建立拼接反射镜热变形前后的平面方程，通过计算TDICCD顶点关于反射镜平面方程的镜像点得出反射镜热变形对TDICCD共线性和共面性的影响；其次，为了对热稳定性进行有效评价，以MTF为其评价函数，分别对TDICCD的共线性误差、共面性误差对TDICCD相机MTF的影响进行了分析，给出了两种误差引起MTF下降的计算公式；最后，以某测绘相机光学拼接焦面为例，对拼接反射镜的热变形引起的探测器的共线性和共面性进行分析，并对不同积分级数下传递函数的下降进行了分析。结果表明，当积分级数为128级时，TDICCD共线性误差引起的飞行方向（向）MTF下降近似为零，在线阵方向（向）MTF下降小于0.025%；共面性误差引起的MTF下降小于0.05%。

光学拼接 反射镜 焦平面 调制传递函数 时间延迟积分电荷耦合器件 热稳定性 测绘相机 航天遥感

0 引言

宽成像谱段､高分辨率､大幅宽及实时传输是目前空间光学遥感器的发展方向｡通过增加光学系统的焦距可以得到更高的分辨率，而大焦距相机想要获得相同的地面覆盖范围需要有更大的视场[1-2]｡焦平面拼接技术是实现大视场的有效手段。

光学拼接利用拼接反射镜的分光原理，将视场分割到不同的空间位置，用多片探测器的像元首尾精密重叠，在像面上形成大视场的探测器阵列。光学拼接有多种方法，如多系统拼接、二次成像拼接和分光路拼接等[3-8]。

目前，应用于空间光学遥感器的探测器有多种，时间延时积分电荷耦合器件(TDICCD)是其中应用最广泛的一种[9]。TDICCD通过多级积分增加探测器的曝光时间，从而提高相机的灵敏度和信噪比[10-11]。当TDICCD积分级数为级时，能量利用率提高了倍，信噪比提高了[12]。

TDICCD由于技术和工艺的限制，单片探测器不能满足视场宽度的要求。实现大视场、宽覆盖时，采用多个TDICCD拼接来增大焦平面视场已成为当前航天测绘遥感相机满足大视场需求的主要手段[13-18]。

调制传递函数（MTF)是评价航天遥感相机的重要指标之一，光学拼接焦平面的共面性和共线性误差会引起TDICCD相机的MTF下降。

本文以某立体测绘TDICCD相机光学拼接焦平面为例，在三维欧氏空间建立反射镜变形前的平面方程（用π0表示）。利用CAE软件对光学拼接焦面的拼接反射镜的热变形进行了分析。提取拼接反射镜变形后反射面上的点，利用最小二乘法拟合变形后拼接反射镜的平面方程（用π1表示）。在此基础上对拼接反射镜热变形引起的TDICCD器件的共线性和共面性误差进行分析，并计算出共线性和共面性误差对TDICCD相机的MTF的影响。

1 焦平面共线性和共面性误差分析

1.1 光学拼接焦平面

图1为某立体测绘相机焦平面的模型示意图。焦平面采用6片TDICCD器件拼接而成，像元大小7μm×7μm，TDICCD沿线阵方向长度为86.016mm，TDICCD宽度方向为16mm，见图1（a）。采用三片共面的拼接反射镜将像面分成等光程的6部分，分别对应6片TDICCD器件。定义焦平面上光路直接到达的区域为透射区，光路经过拼接反射镜反射后到达的区域为反射区。焦平面透射区和反射区相互垂直，拼接反射镜位于透射区和反射区角平分面上，保证透射区和反射区等光程，见图1（b）。

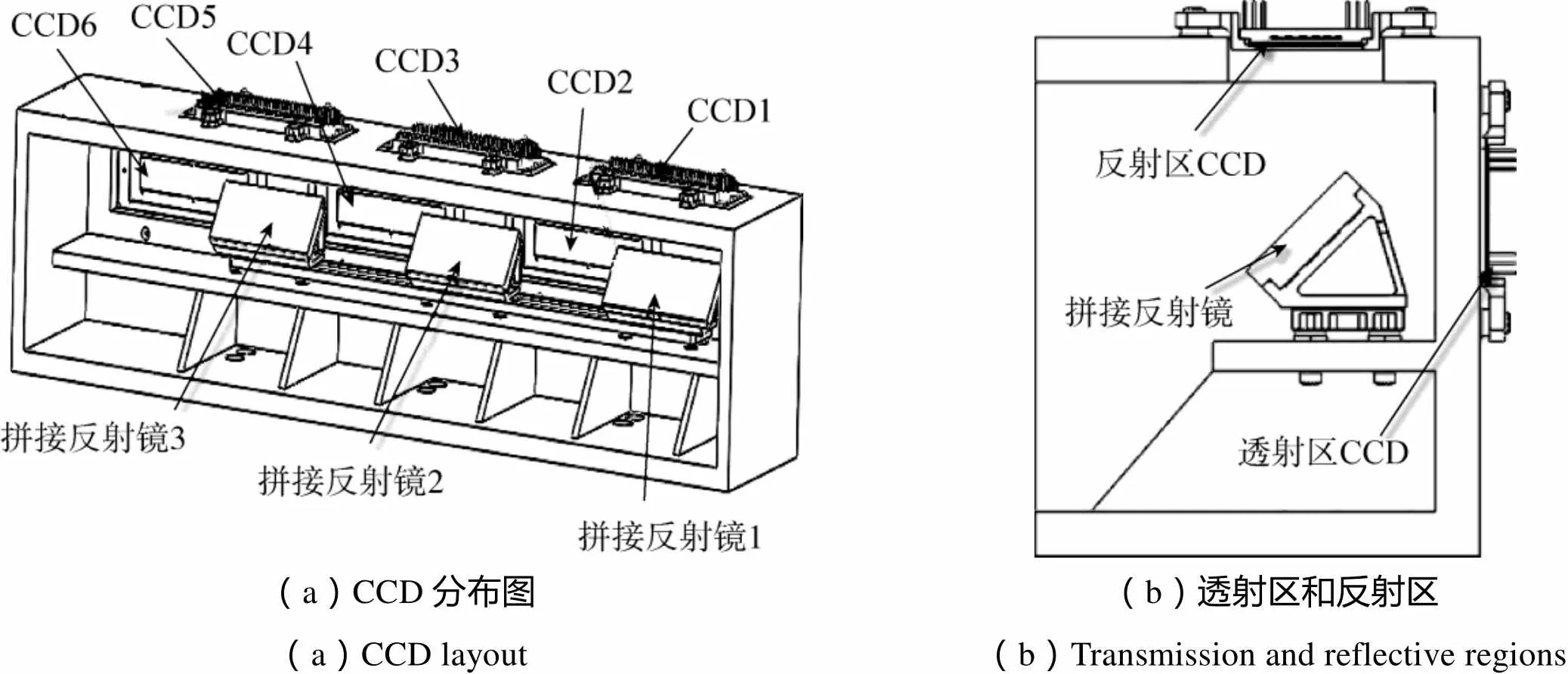
（a）CCD分布图（a）CCD layout（b）透射区和反射区（b）Transmission and reflective regions

CCD拼接时，以CCD4为基准，CCD1、CCD3、CCD5位于反射区，CCD2、CCD4、CCD6位于透射区。当拼接反射镜发生热变形时，与反射镜对应的CCD1、CCD3和CCD5的共面性和共线性会发生变化，进而影响相机的成像品质。

1.2 坐标系建立

在三维欧氏空间建立右手坐标系，沿CCD线阵方向为轴，飞行方向为轴，垂直CCD感光面为轴，坐标原点位于CCD感光面边缘中心。图2为反射镜与CCD空间位置图。

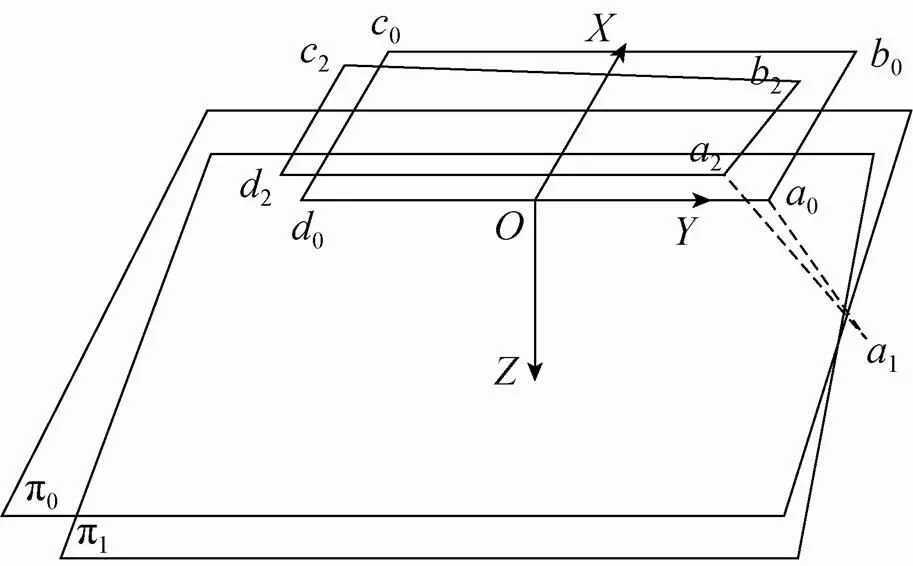
图2 反射镜与CCD空间位置

在坐标系中，定义π0为拼接反射镜变形前平面方程，π1为拼接反射镜变形后平面方程。令平面π0的法向量为，平面π1的法向量为，可知平面π0和平面π1在坐标系-中的平面方程为

式中0为平面π0的常数项；1为平面π1的常数项。

定义0、0、0、0为反射区CCD的4个顶点，1为0关于平面π0的镜像点，2为1关于平面π1的镜像点，即2为0关于平面π0和π1两次镜像后的点。同理，定义2、2、2为0、0、0关于平面π0和π1两次镜像后的镜像点。

在坐标系中分别定义0、1、2、0、0、0、2、2、2坐标为，，，，，，，，。

1.3 误差计算公式

根据几何光学成像原理，当拼接反射镜所在平面由π0变到π1之后，对应的像面上的点0变化到2位置。同理可得CCD上点0、0、0在拼接反射镜变化之后的对应点为2、2、2。图3为CCD镜像前后的位置示意图。根据空间解析几何，由0、0、0、0的坐标值以及拼接反射镜变形前后的平面方程π0和π1可求出2、2、2、2的坐标值[19]，式（3）~（8）以2为例给出了其坐标值，同理可以得出2、2、2点坐标值。

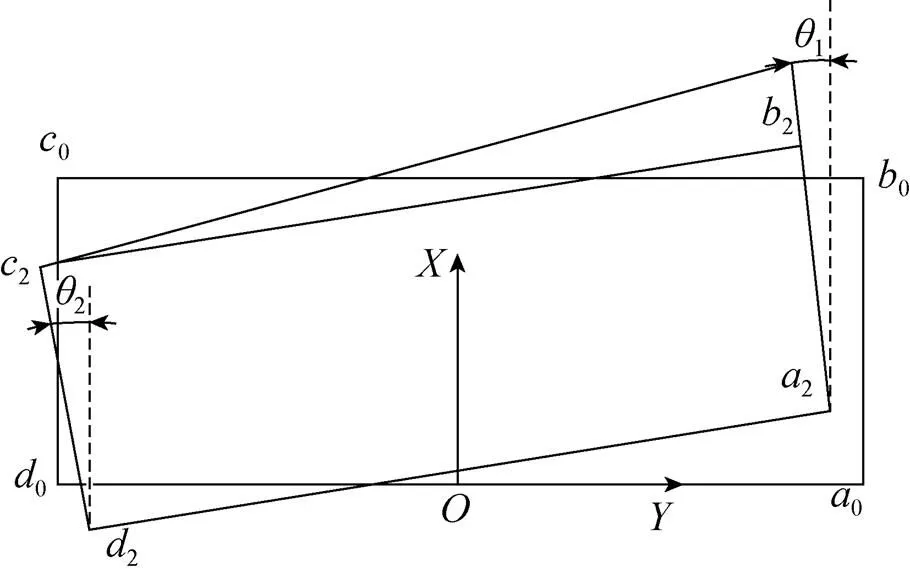
图3 CCD镜像前后的位置示意图

进而可得

式中

在坐标系-中，定义CCD的共面性误差和共线性误差为别为Δ和Δ则有

定义1为直线22和00夹角，2为直线22和00夹角，由于夹角1和2很小，则有

定义反射镜变形前后反射区TDICCD积分方向变化角度为，则可近似表示为

1.4 误差计算

在Hyperworks软件里建立焦平面CAE仿真模型，并对焦平面的热变形进行仿真计算，结果如图4所示。

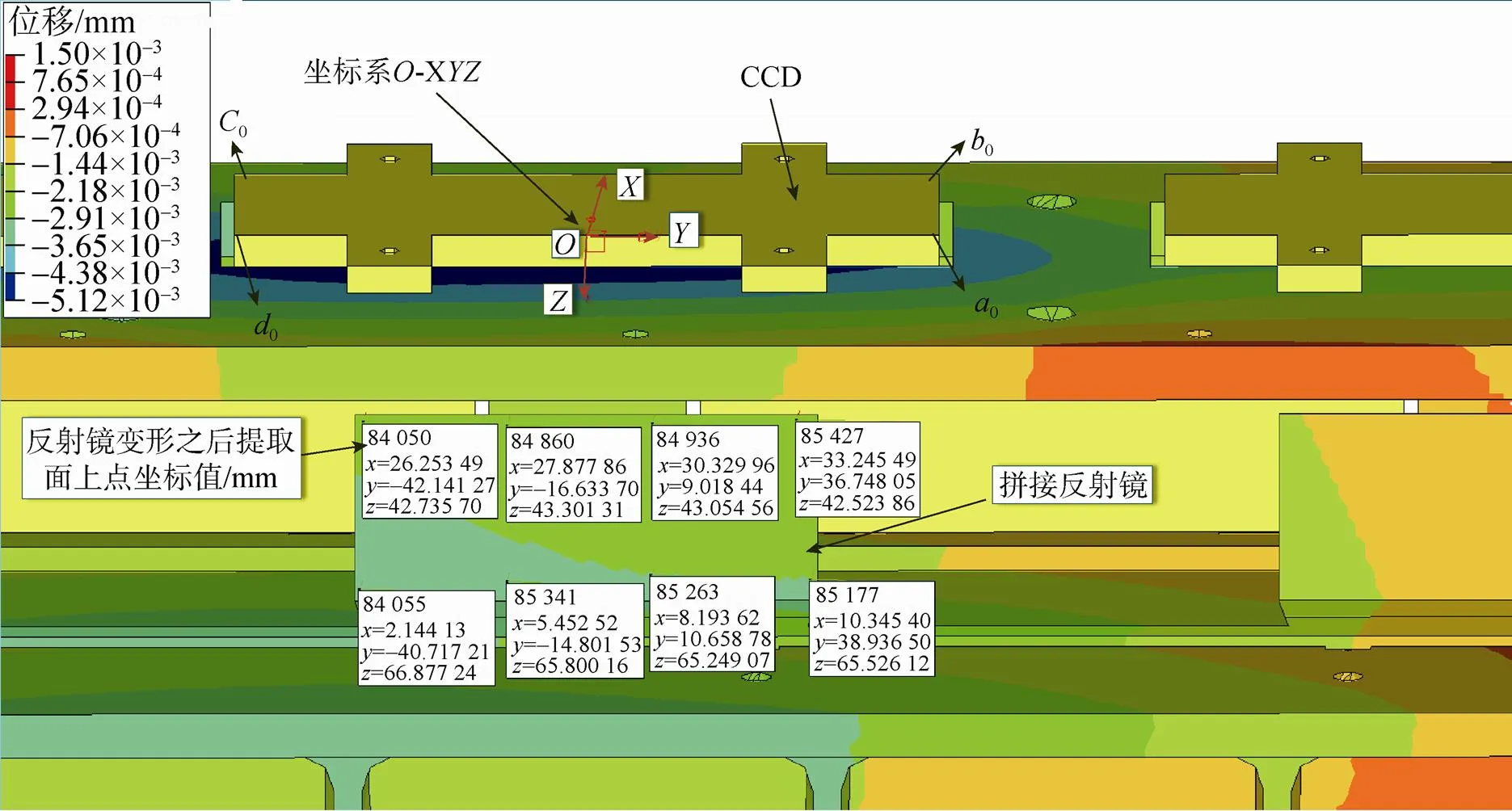
图4 热变形仿真结果

在CCD上建立右手坐标系。在热变形前的反射镜上任意提取三点的坐标值。通过三点的坐标值可得反射镜变形前的平面方程π0。在变形后的拼接反射镜上提取20个点的坐标值(图中只示意其中8个点的坐标值)，在Matlab软件中通过最小二乘法拟合出反射镜变形后的平面方程π1。

通过式（9）、（10）、（13）可以得出CCD四个顶点在拼接反射镜变形后的共线性误差、共面性误差和TDICCD积分方向变化角度值。

分别对拼接反射镜1、拼接反射镜2、拼接反射镜3采用上述方法进行分析计算，可以得出三片CCD的共面性误差、共线性误差和TDICCD积分方向变化角度值，如表1所示。

表1 三片CCD的共面共线误差

Tab.1 The errors of three CCDs’ collinear and coplanar

通过上述分析可以看出，CCD5的共面性和共线性误差最大，共面性误差为2μm，共线性误差为1.2μm，TDICCD积分方向变化角度为0.3″。

2 MTF下降分析

2.1 共线性误差引起MTF下降分析

拼接反射镜热变形导致反射区CCD的共线性误差，引起TDICCD成像时的像移。像移造成相机在飞行方向（即垂直CCD线阵方向，相机的轴）和垂直分行方向（CCD线阵方向，相机轴）的光学MTF降低，从而影响系统的成像品质。

由像移引起的MTF下降为[20]

在这里，讨论在奈奎斯特频率f下TDICCD积分方向变化角度值对MTF的影响，因为，所以在垂直线阵方向（向）和沿线阵方向（向）的MTF为

式中为TDICCD积分级数；为像元大小；为TDICCD积分方向变化角度。

在空间频率为71.6线对/mm处，在不同积分级数下（最大积分级数128级），对反射区三片CCD的垂直线阵方向（向）和沿线阵方向（向）的MTF分别进行求解，如图5~7所示。

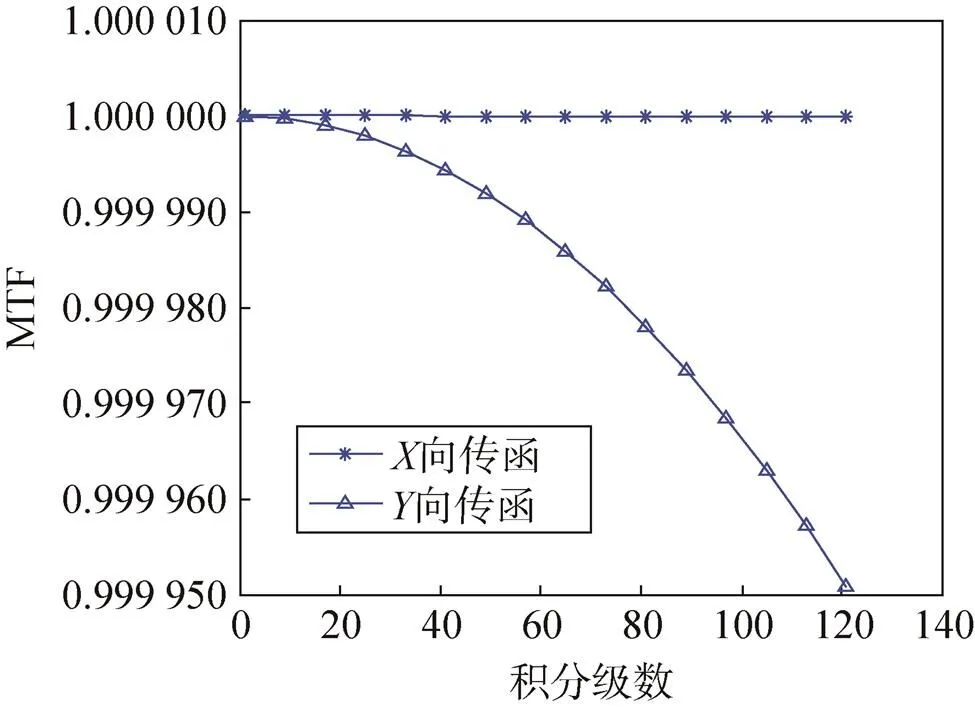
图5 CCD1不同积分级数下的MTF

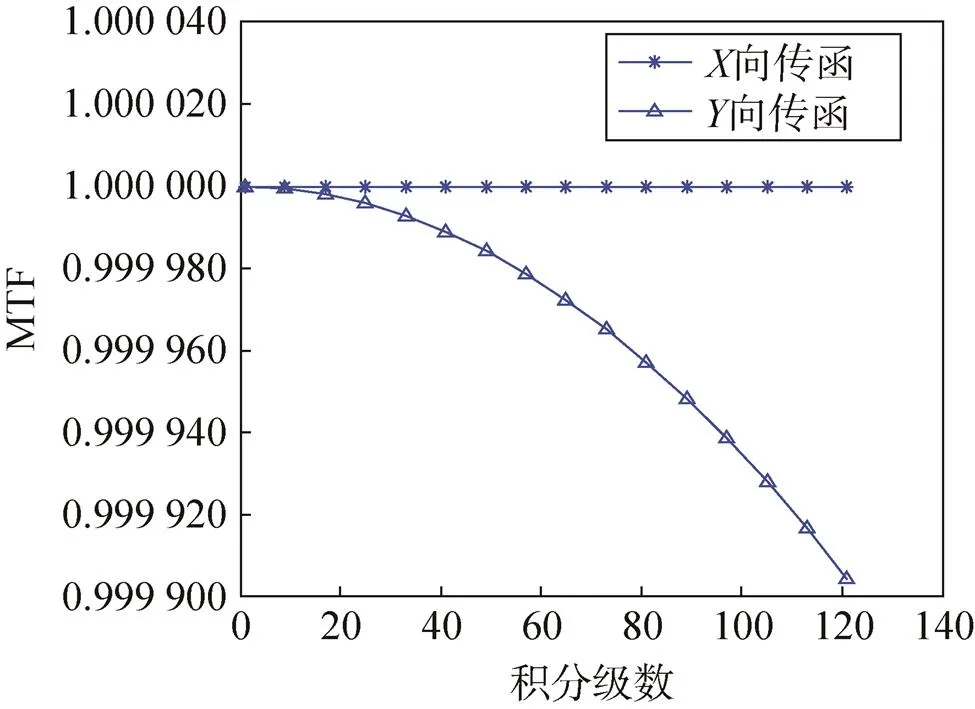
图6 CCD3不同积分级数下的MTF

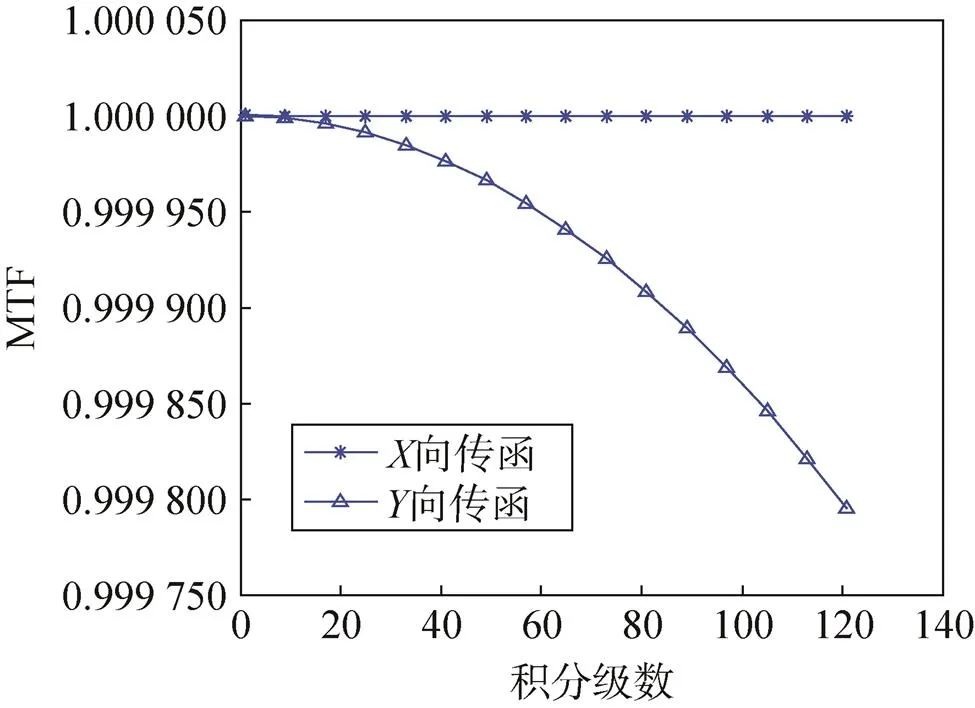
图7 CCD5不同积分级数下的MTF

通过上述的分析可以看出，在不同积分级数下，三片CCD在向MTF下降近似为零，在向，当积分级数为128级时，MTF下降小于2.5‱。

2.2 共面性误差引起MTF下降分析

以CCD4为基准，拼接反射镜热变形引起反射区的CCD产生了离焦量（即CCD共面性误差Δ），从而引起相机MTF下降。

光学系统成像时，点光源在像平面上发生弥散，可以认为点光源在像平面上呈一圆盘状的像。当出现离焦时，其半径为，Δ为离焦量；为光学系统的F数，=/，为相机焦距，为入瞳直径。CCD的离焦量Δ引起的MTF下降可表示为[21]

式中 J1（·）为一阶贝塞尔函数；N为空间频率。

当像元尺寸7μm，=10，在奈奎斯特频率N71.6线对/mm下，Δ对TDICCD相机的MTF影响曲线如图8所示。

图8 不同空间频率处CCD共面性误差引起的传函下降

由上述结果可以看出，反射镜热变形引起的CCD共面性误差对MTF的影响很小，在空间频率为71.6线对/mm处，MTF最大下降小于0.05%。

3 结束语

本文首先介绍了拼接反射镜的热稳定性对光学拼接焦平面共线性和共面性的影响机理，在三维欧式空间建立数学模型，并给出了计算公式。CCD共线性误差和共面性误差会引起TDICCD相机MTF下降。

以某航天测绘相机光学拼接焦平面为例，对拼接反射镜的热变形引起反射区CCD的共线性和共面性误差进行了计算。最后，计算了共线性和共面性误差对相机MTF下降的影响。得出以下结论：

1）共线性误差引起的向MTF下降近似为零，可忽略不计；

2）共线性误差引起的向MTF下降影响有限，当TDICCD积分级数为128时，MTF下降小于0.025%；

3）共面性误差引起的MTF下降小于0.05%；

4）测绘相机光学拼接焦平面光学拼接反射镜的热稳定性能对相机MTF影响有限，能够满足设计要求。

[1] 刘明, 修吉宏, 刘钢, 等. 国外航空侦察相机的发展[J]. 电光与控制, 2004, 11(1): 56-59. LIU Ming, XIU Jihong, LIU Gang, et al. Developments of Overseas Aerial Reconnaissance Camera[J]. Electronics Optics & Control, 2004, 11(1): 56-59. (in Chinese)

[2] 徐彭梅, 杨桦, 伏瑞敏, 等. CBERS-1卫星CCD相机的光学拼接、配准和定焦[J]. 航天返回与遥感, 2001, 22(3): 12-15. XU Pengmei, YANG Hua, FU Ruimin, et al. Optical Butting, Registration and Focus-fixing of CCD Camera for CBERS-1 Satellite[J]. Spacecraft Recovery & Remote Sensing, 2001, 22(3): 12-15. (in Chinese)

[3] 何昕, 魏仲慧, 郝志航. 基于单心球面系统的九块面阵CCD数字拼接[J]. 光学精密工程, 2003, 11(4): 421-424. HE Xin, WEI Zhonghui, HAO Zhihang. Digital Camera Modeling of Butting 9 CCD Chips in the Concentric Spherical Lens System[J]. Optics and Precision Engineering, 2003, 11(4): 421-424. (in Chinese)

[4] ANEKO Y, SAITOH M, HAMAGUCHI I, et al. Image Forming Apparatus for Forming Image Corresponding to Subject, by Dividing Optical Image Corresponding to the Subject into Plural Adjacent Optical Image Parts: US5194959[P]. 1993-03-16.

[5] YANG Chenghai. A High-resolution Airborne Four-Camera Imaging System for Agricultural Remote Sensing[J]. Computers and Electronics in Agriculture, 2012, 88(10): 13-24.

[6] HARVEY R P. Optical Beam Splitter and Electronic High Speed Camera Incorporating such a Beam Splitter: US5734507[P]. 1998-03-31.

[7] 雷华, 徐之海, 冯华君, 等. 光学拼接成像系统[J]. 仪器仪表学报, 2010, 31(6): 1213-1217. LEI Hua, XU Zhihai, FENG Huajun, et al. Optical Butting System[J]. Chinese Journal of Scientific Instrument, 2010, 31(6): 1213-1217. (in Chinese)

[8] SADOWSKI H. Large Time Delay and Integration Focal Plane Assembly with an Optically Contiguous Pixel Format[C]. Proc. SPIE 0217, Advances in Focal Plane Technology. Los Angeles, California, USA, 1980.

[9] 李丙玉, 王晓东, 李哲. 在轨完成CCD非均匀性校正的方法[J]. 液晶与显示, 2011, 26(2): 255-259. LI Bingyu, WANG Xiaodong, LI Zhe. Method of CCD Non-Uniformity Correcting in Orbit[J]. Liquid Crystals and Displays, 2011, 26(2): 255-259. (in Chinese)

[10] 童子磊. CCD相机的像移补偿技术[J]. 激光与红外, 2005, 35(9): 628-632. TONG Zilei. Compensation Technology for the Image Motion of CCD Camera[J]. Laser & Infrared, 2005, 35(9): 628-632. (in Chinese)

[11] 闫得杰, 徐抒岩, 韩诚山. 飞行器姿态对空间相机像移补偿的影响[J]. 光学精密工程, 2008, 16(11): 2199-2203. YAN Dejie, XU Shuyan, HAN Chengshan. Effect of Aerocraft Attitude on Image Motion Compensation of Space Camera[J]. Optics and Precision Engineering, 2008, 16(11): 2199-2203. (in Chinese)

[12] 樊超, 李英才, 易红伟. 偏流角对TDI CCD相机像质的影响分析[J]. 光电工程, 2007, 34(9): 70-73. FAN Chao, LI Yingcai, YI Hongwei. Influence Analysis of Drift Angle on Image Quality of TDI CCD Camera[J]. Opto-Electronic Engineering, 2007, 34(9): 70-73. (in Chinese)

[13] 任建岳, 孙斌, 张星祥, 等. TDICCD交错拼接的精度检测[J]. 光学精密工程, 2008, 16(10): 1852-1857. REN Jianyue, SUN Bin, ZHANG Xingxiang, et al. Precision Measurement of TDICCD Interleaving Assembly[J]. Optics and Precision Engineering, 2008, 16(10): 1852-1857. (in Chinese)

[14] 吕恒毅, 刘杨, 郭永飞. 遥感相机焦面CCD机械拼接中重叠像元数的确定[J]. 光学精密工程, 2012, 20(5): 1041-1047. LV Hengyi, LIU Yang, GUO Yongfei. Computation of Overlapping Pixels of Mechanical Assembly CCD Focal Planes in Remote Sensing Cameras[J]. Optics and Precision Engineering, 2012, 20(5): 1047-1047. (in Chinese)

[15] ROGALSKI A. Progress in Focal Plane Array Technologies[J]. Progress in Quantum Electronics, 2012, 36(2): 342-473.

[16] 郭疆, 龚大鹏, 朱磊, 等. 测绘相机焦平面CCD交错拼接中重叠像元数计算[J]. 光学精密工程, 2013, 21(5): 1251-1256. GUO Jiang, GONG Dapeng, ZHU Lei, et al. Calculation of Overlapping Pixels in Interleaving Assembly of CCD Focal Plane of Mapping Camera[J]. Optics and Precision Engineering, 2013, 21(5): 1251-1256. (in Chinese)

[17] SULTANA J A, O’Neill M B. Design, Analysis and Testing of a CCD Array Mounting Structure[C]. Proc. SPIE 1532, Analysis of Optical Structures. San Diego, California, USA, 1991.

[18] JORDEN P R, MORRIS D G, POOL P J. Technology of Large Focal Planes of CCDs[C]. Proc. SPIE 5167, Focal Plane Arrays for Space Telescopes. San Diego, California, USA, 2004.

[19] 朱鼎勋, 陈绍菱. 空间解析几何学[M]. 北京: 北京师范大学出版社, 1984. ZHU Dingxun, CHEN Shaoling. Analytic Geometry of Space[M]. Beijing: Beijing Normal University Publishing House, 1984. (in Chinese)

[20] 肖占全, 翟林培, 丁亚林, 等. 光学拼接误差对TDI-CCD相机的影响[J]. 半导体光电, 2008, 29(5): 795-798. XIAO Zhanquan, ZHAI Linpei, DING Yalin, et al. Research of Optical Assembly Errors Effects on TDI-CCD Camera[J]. Semiconductor Optoelectronics, 2008, 29(5): 795-798. (in Chinese)

[21] 耿文豹, 翟林培, 丁亚林. 振动对光学成像系统传递函数影响的分析[J]. 光学精密工程, 2009, 17(2): 314-320. GENG Wenbao, ZHAI Linpei, DING Yalin. Analysis of Influence of Vibration on Transfer Function in Optics Imaging System[J]. Optics and Precision Engineering, 2009, 17(2): 314-320. (in Chinese)

Influence on MTF of Mirror Thermal Stability in Focal Plane

LI Fuqiang CAI Weijun FAN Junjie

（Beijing Institute of Mechanics & Electricity, Beijing 100094, China）

The optical butting is an effective technology for broadening view field of camera. During optical butting of focal plane assembly（FPA）, the thermal stability of reflector has effect on linearity and coplanarity. The linear error and coplanar error will cause a decline of the modulation transfer function（MTF）. In this paper, firstly, the plane equation of the reflector before and after the thermal deformation is established in the 3-dimensional Euclidean space. The linear error and coplanar error are calculated by mirroring the CCD vertex. Secondly, in order to evaluate the thermal stability, the MTF is present as the evaluation index. The negative impacts of linear error and coplanar error on TDICCD camera's MTF are analyzed. Calculation formulas of MTF caused by the two errors are deduced. Finally, taking an example of a mapping camera, the linear error and coplanar error of the FPA are analyzed. The influence on decline of the dynamic MTF is analyzed with different integral grades. The results prove that the decline of the dynamic MTF caused by linear error is approximately zero indirection and less than 0.025% indirection with an integral grade of 128, and the decline of the dynamic MTF caused by linear error is less than 0.05%.

optical butting; reflector; focal plane assembly; modulation transfer function; time delay integration charge coupled device; thermal stability; mapping camera; space remote sensing

（编辑：王丽霞）

V447

A

1009-8518(2016)03-0075-07

10.3969/j.issn.1009-8518.2016.03.009

李富强，男，1985生，硕士，毕业于哈尔滨工业大学机械电子工程系，工程师。研究方向为空间光学遥感器焦面设计以及结构稳定性分析。E-mail：lfq19851126@163.com。

2016-02-03

国家重大科技专项工程