降落伞稳降阶段的SPH方法数值模拟
姚向茹余莉吴琼
降落伞稳降阶段的SPH方法数值模拟
姚向茹余莉吴琼
(南京航空航天大学航空宇航学院,南京 210016)
随着计算机技术的不断发展以及数值模拟技术的兴起,对降落伞力学特性的模拟日益精确。为了消除传统降落伞模拟中因网格大变形而产生负体积的影响,文章采用光滑粒子流体动力学方法,对选定降落伞模型开展了稳降阶段的流固耦合数值模拟,计算得到的气动力系数与风洞试验结果较为一致。研究了空气粒子密度对数值结果的影响,结果表明,粒子密度过少,降落伞结构单元难以和流场实现有效耦合,计算精度降低;但粒子密度超过一定值,不仅会增加计算消耗,也会增加舍入误差而影响计算精度,确定了最佳粒子数。在此基础上,模拟了不同初速度下降落伞的下降过程,获得了降落伞外形、投影直径、下降速度、降落伞气动力及伞衣摆角的动态变化情况。数值结果表明伞衣的呼吸频率、稳定后的平衡速度和气动力受速度影响较小,但速度增加,伞衣呼吸强度及摆角增加,且摆动角度的衰减性要低于投影直径的衰减能力。SPH模拟方法有效地回避了降落伞流固耦合的网格大变形问题,在柔性大变形流固耦合问题上有广阔的应用前景。
下降过程 流固耦合 光滑粒子流体动力学方法 降落伞
0 引言
降落伞系统作为一种高效、可靠的回收装置,在载人飞船、返回式卫星的回收着陆以及火星探测器的着陆等过程中,都得到了广泛的应用。降落伞工作过程是流场结构剧烈作用的高度非线性过程,长期以来大量依赖于工程试验。随着数值算法的不断进步和计算机硬件水平的提高,采用流场结构耦合分析方法进行降落伞工作过程研究受到国内外学者的日益关注[1-3]。
早期基于时空离散的降落伞流固耦合方法主要是CFD/MSD模型,将降落伞离散成一系列由弹性力、阻尼力联系的质点,在流场力的作用下,质点发生运动[4-5]。之后,基于DSD/SST界面跟踪技术进行降落伞流固耦合问题的研究成为比较通用的一种方法,在翼伞、十字形伞和环帆伞等的三维流固耦合计算中得到了应用[6-9]。上述方法,流场计算均是采用基于网格的控制体积法或有限元法进行,对于大变形开伞过程,易产生负体积;而对于伞载系统发生运动时,更需要巨大的计算消耗。
光滑粒子流体动力学(SPH)方法不需要生成网格,完全消除自由边界上的数值发散,更避免了网格扭曲与网格重构等问题,能够十分方便地模拟网格大变形问题[10],在高速碰撞数值模拟[11-12]、高能炸药的爆炸及水下爆炸冲击等问题[13-15]均得到了很好的应用。由于SPH方法粒子的运动与流体或气体运动相似,SPH粒子方法也应用在粘性流体模拟[16]、风沙运动模拟[17]以及液固撞击数值模拟[18]方面,文献[19]中采用SPH方法模拟了跨膜流动,但该方法在降落伞的流固耦合模拟上还鲜有报道。
本文采用SPH方法成功实现了降落伞稳降阶段流固耦合数值模拟,得到了伞衣外形、应力分布、速度、气动力以及摆动角度的变化情况,数值结果符合工程实际情况;分析了空气粒子密度、降落伞速度对稳降过程的影响。SPH模拟方法为降落伞流固耦合模拟提供了一个新的研究手段。
1 数学模型
1.1 流场SPH控制方程
连续流体的基本守恒方程组:
SPH离散可以写成:
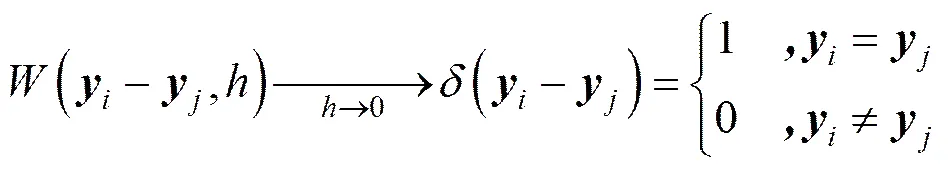
式中、分别为粒子和粒子的三维坐标向量;为狄拉克函数;为定义光滑函数的影响区域的光滑长度。
1.2 FEM-SPH耦合算法实现
对于降落伞,采用有限元方法(FEM)求解,其控制方程为:
耦合计算通过罚函数接触算法实现,在流场SPH粒子与有限元结构单元表面之间引入一个界面接触力,限制SPH粒子对结构单元的穿透,从而模拟固体和流体之间的相互作用。
界面接触力(法向F,切向F)的计算公式为:
2 数值模型
本文计算以风洞试验的伞衣幅数为8幅的平面圆形伞作为数值模拟对象[20],载荷质量为1.2kg,空气密度为1.2kg/m3,伞顶孔直径0.1m,具体计算参数如表1所示。为了简化问题,伞衣初始外形假设为半球形(图1)。伞衣选用薄壳三角形单元,网格数为1 674,伞绳采用一维梁单元,网格数为400。流场计算采用长方体计算区域,长、宽、高方向尺寸为10m×10m×10m。流场模型如图2所示。
表1 降落伞计算参数

Tab.1 Calculating parameters of parachute

图1 降落伞模型

图2 流场模型
3 数值结果及分析
3.1 粒子密度对数值结果的影响
为了研究粒子密度对数值结果的影响,在其他参数保持不变的情况下,对流场域进行了三种粒子密度的计算,粒子数目分别为125 000、300 763和512 000,初始速度为40m/s。
图3为三种粒子密度下降落伞的稳降过程。图4和图5分别表示降落伞在不同粒子密度下运动的速度和受力变化情况,稳定后的数值结果平均值见表2所示。从中可以看出,假设条件以及计算软件精度会对结果产生一定影响,造成计算误差。此外,粒子数过稀,计算初期伞绳和流场无法发生有效的相互作用,伞衣前方受扰流场小,流场与伞衣的相互作用减弱,稳态时气动力和气动力系数均较小,和文献[20]风洞试验数据(气动力系数为0.738)相比,误差接近19%。当粒子数达到51万时,阻力系数计算误差高于30万粒子数的2.42%,同时计算机时增加了0.6倍。
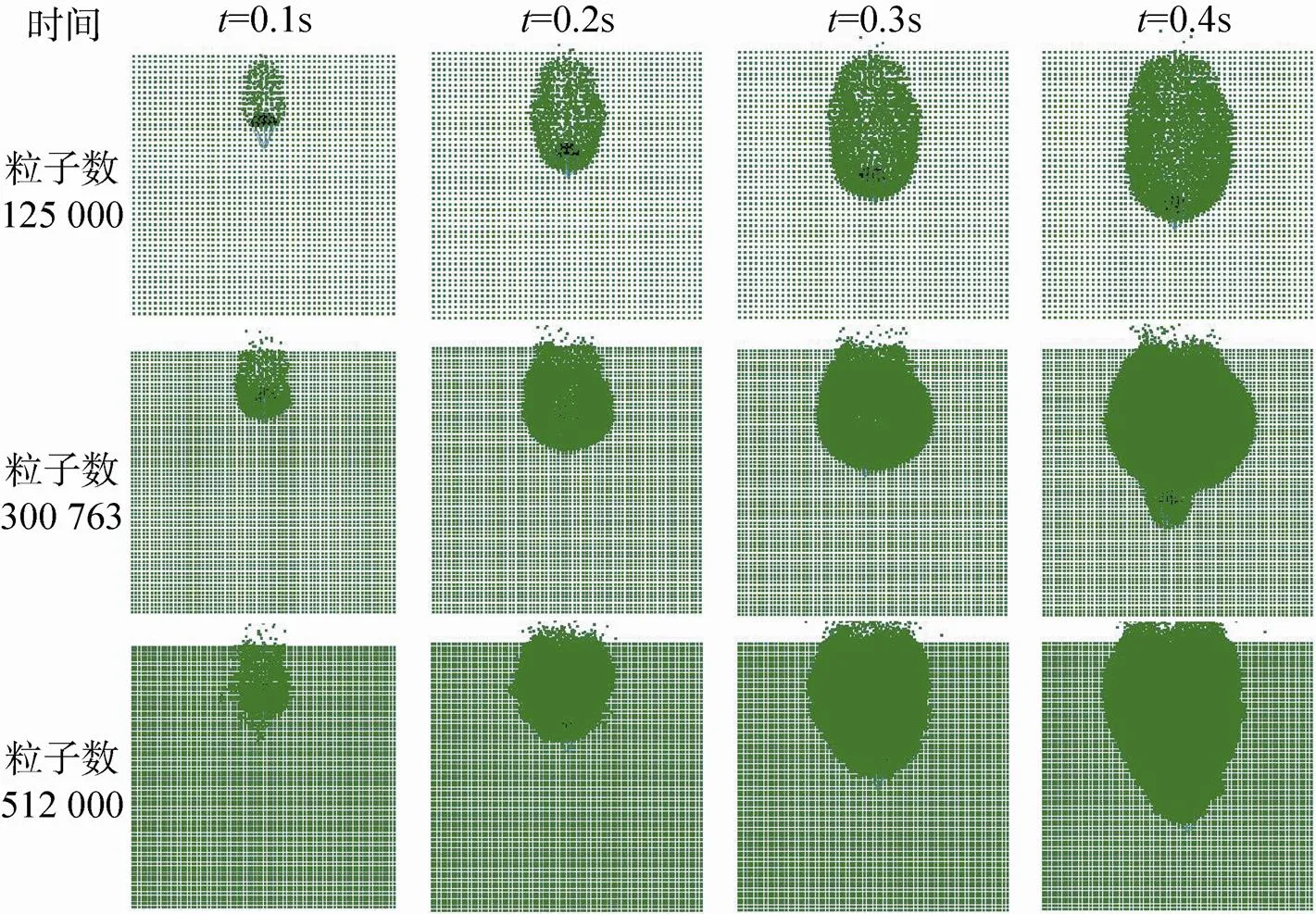
图3 降落伞稳降过程

图4 降落伞的速度(不同粒子密度)
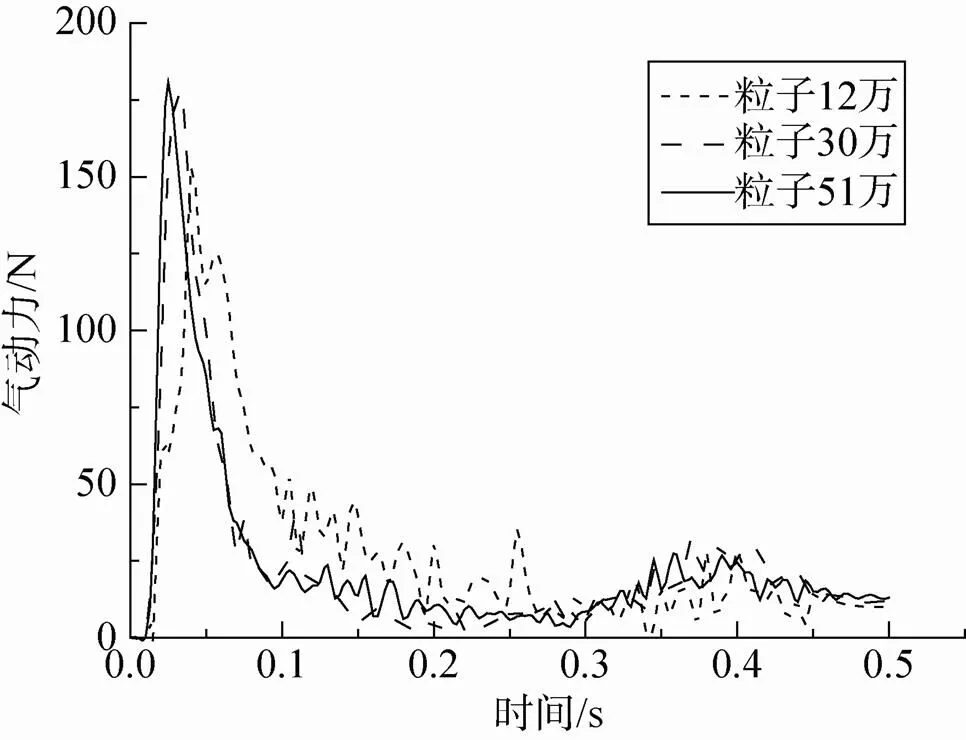
图5 降落伞的受力情况(不同粒子密度)
表2 稳态数值结果

Tab.2 Numerical results
可见,粒子数过稀,伞衣和流场无法发生有效的流固耦合作用,导致数值计算结果误差较大;但当粒子数过高时,不仅会大大增加计算消耗,同时也会因为离散点较多,求解计算次数增加而导致舍入误差过大影响计算精度,对于本文研究对象,30万粒子数较为合理。
3.2 不同速度稳降阶段工作特性分析
在30万流场粒子数下,本文模拟了30m/s、40m/s和50m/s初始速度下降落伞的下降情况,计算结果如图6~图9所示。

图6 降落伞投影直径变化
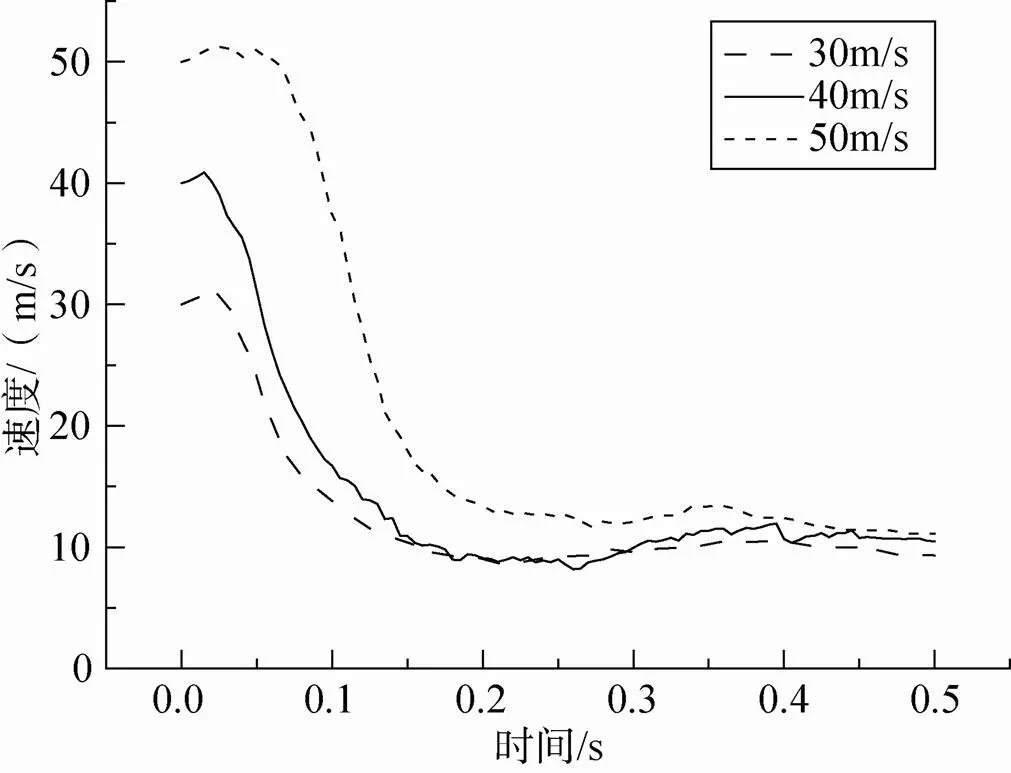
图7 降落伞速度
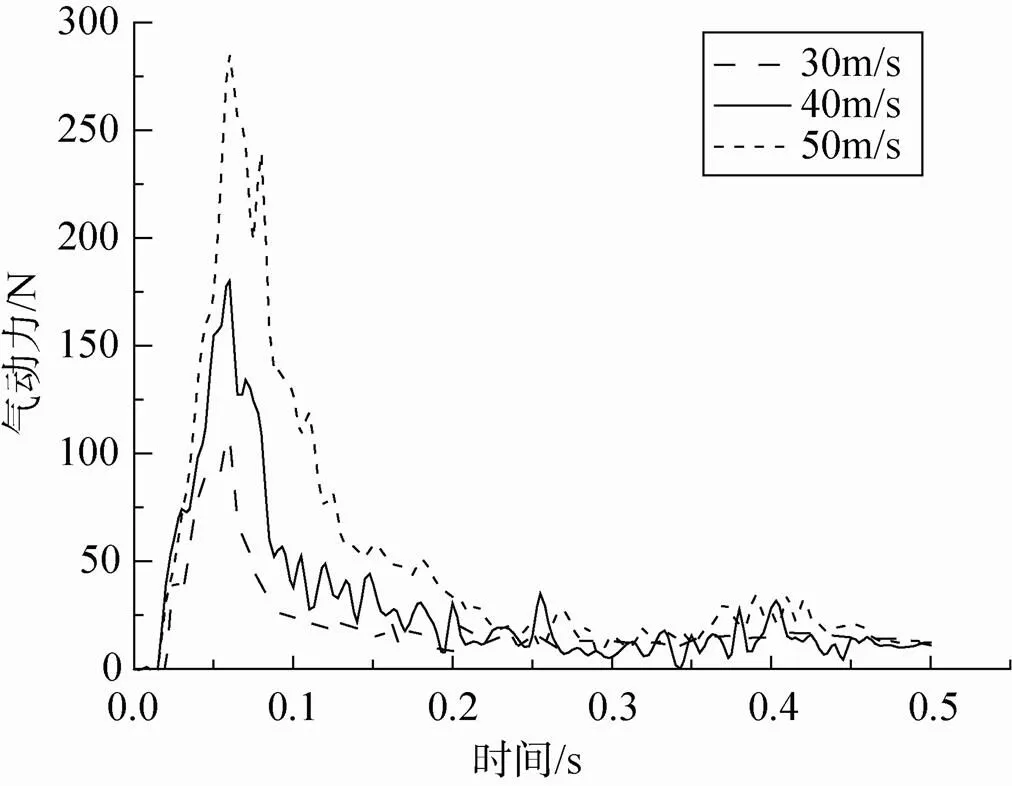
图8 降落伞受力情况

图9 降落伞轴线摆动角度
图6表示三种工况下降落伞投影直径的变化。降落伞在下降过程中伞衣底边会收缩,达到最小,然后又慢慢张开达到最大,伞衣的呼吸频率受速度影响很小,但速度增加,呼吸强度加强。
图7~图8分别为降落伞下降速度及轴向气动力随时间的变化曲线。速度越大,初始气动阻力越大,减速度越快,但达到0.2s时,三者差别不大,其稳态时的平均气动力和下降速度几乎趋于一致,和工程实际一致。
图9表示下降过程中降落伞对称轴与下降速度方向之间的夹角。降落伞在下降过程中,伞衣前后左右摆动,初始速度越大,摆角越大。由于运动惯性的影响,摆角的衰减能力远远低于气动力及投影直径的衰减能力,且摆动周期高于投影直径的呼吸周期。
4 结束语
本文以文献[20]风洞试验用伞为研究对象,采用SPH方法展开了不同粒子数目、不同初始速度下降落伞稳降阶段的流固耦合数值模拟,气动力系数和风洞试验结果较为一致,得出如下结论:
1)粒子密度对计算结果有一定影响,数目过少将不能充分地实现结构单元和流场之间的耦合,数目过多不仅会过大增加计算消耗,也会增加数值计算误差。
2)得到了降落伞投影直径的变化情况,表明呼吸频率受速度影响很小,但速度增加,呼吸强度增加。
3)速度越大,初始气动阻力越大,减速度越快,但达到平衡时,降落伞的气动阻力和平衡速度趋于一致。
4)速度越大,降落伞摆动角度越大,稳定性降低。由于惯性影响,摆角的衰减能力远远低于气动力及投影直径的衰减能力。
[1] STEIN K R, BENNEY R J, STEEVES E C. A Computational Model that Couples Aerodynamic Structural Dynamic Behavior of Parachutes during the Opening Process[R].ADA264115, NASA, 1993.
[2] 郭叔伟, 王海涛, 董杨彪, 等. 降落伞呼吸现象研究[J]. 航天返回与遥感, 2010, 31(1): 18-23. GUO Shuwei, WANG Haitao, DONG Yangbiao, et al. Research on Parachute Breath Behavior [J]. Spacecraft Recovery & Remote Sensing, 2010, 31(1): 18-23. (in Chinese)
[3] 连亮, 王中阳, 张红英, 等. 基于ALE方法的群伞稳降阶段的数值模拟[J]. 航天返回与遥感, 2014, 35(1):21-28. LIAN Liang, WANG Zhongyang, ZHANG Hongying, et al. Numerical Simulation of Cluster Parachute System During Steady-state Descent Phase Based on ALE Method[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(1): 21-28. (in Chinese)
[4] YU L, MING X. Study on Transient Aerodynamic Characteristics of Parachute Opening Process[J]. Acta Mechanica Sinica, 2007, 23(6): 627-633.
[5] 余莉, 史献林, 明晓. 降落伞充气过程的数值模拟[J]. 航空学报, 2007, 28(1): 52-57. YU Li, SHI Xianlin, MING Xiao. Numerical Simulation of Parachute during Opening Process[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(1): 52-57. (in Chinese)
[6] KALRO V, TEZDUYAR T E. A Parallel 3D Computational Method for Fluid-structure Interactions in Parachute Systems[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 190(3): 321-332.
[7] STEIN K, BENNEY R, KALRO V, et al. Parachute Fluid-structure Interactions 3-D Computation[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 190(3): 373-386.
[8] STEIN K, BENNEY R, TEZDUYAR T, et al. Fluid-structure Interaction of a Cross Parachute Numerical Simulation[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 191(6): 673-687.
[9] TEZDUYAR TE, SATHE S, SCHWAAB M, et al. Fluid-structure Interaction Modeling of Ringsail Parachutes[J]. Computational Mechanics, 2008, 43(1): 133-142.
[10] FOSTER N, FEDKIW R. Practical Animation of Liquids[C]. Proceedings of International Conference on Computer Graphics and Interactive Techniques. Standford: Stanford University, 2001: 23-30.
[11] LIBERSKY L D, RANDLES P W, CAMEY TC, et al. Recent Improvements in SPH Modeling of Hypervelocity impact[J]. International Journal of Impact Engineering, 1997, 20(6): 525-532.
[12] LIBERSKY L D, PETSCHEK A G, CAMEY T C, et al. High Strain Lagrangian Hydrodynamics: A Three-dimensional SPH Code for Dynamic Material Response[J]. Journal of Computational Physics, 1993, 109(1): 67-75.
[13] LIU M B, LIU G R, ZONG Z, LAM KY. Computer Simulation of High Explosive Explosion Using Smoothed Particle Hydrodynamics Methodology[J]. Computers and Fluids, 2003, 32(3): 305-322.
[14] LIU M B, LIU G R, ZONG Z, et al. Smoothed Particle Hydrodynamics for Numerical Simulation of Underwater Explosions[J]. Computational Mechanics, 2003, 30(2): 106-118.
[15] LIU M B, LIU G R, LAM K Y. Investigations into Water Mitigations using a Meshless Particle Method[J]. Shock Waves, 2002, 12(3):181-195.
[16] 金善勤, 郑兴, 段文洋. 改进 SPH 方法在GPU并行中对粘性流场的模拟[J]. 哈尔滨工程大学学报, 2015, 36(8): 1-7. JIN Shanqin, ZHENG Xing, DUAN Wenyang. Viscosity Flow Simulation by Using Improved SPH Method Based on GPU Parallel Calculation[J]. Journal of Harbin Engineering University, 2015, 36(8): 1-7. (in Chinese)
[17] 陈福振, 强洪夫, 高巍然. 风沙运动问题的SPH-FVM耦合方法数值模拟研究[J]. 物理学报, 2014, 63(13): 14-26. CHEN Fuzhen, QIANG Hongfu, GAO Weiran. Smoothed Particle Hydrodynamics Algorithm and Finite Element Method Applied in Numerical Simulation of the Sand Movement Problem[J]. Acta Phys. Sin., 2014, 63(13): 14-26. (in Chinese)
[18] 王安文, 徐绯, 张岳青. SPH方法在液固撞击数值模拟中的应用[J]. 计算物理, 2012, 29(4): 525-533. WANG Anwen, XU Fei, ZHANG Yueqing. Smoothed Particle Hydrodynamics Algorithm Applied in Numerical Simulation of Fluid-solid Impact[J]. Chinese Journal of Computational Physics, 2012, 29(4): 525-533. (in Chinese)
[19] 初阳, 卢文强. 多孔介质中流体输运的孔尺度SPH模拟[J]. 工程热物理学报, 2009, 30(3): 437-440. CHU Yang, LU Wenqiang. Porescale SPH Simulation of Flow in Porous Media[J]. Journal of Engineering Thermophysics, 2009, 30(3): 437-440. (in Chinese)
[20] 余莉, 明晓, 陈丽君. 不同透气情况降落伞的流场试验研究[J]. 空气动力学学报, 2008, 26(1):19-25. YU Li, MING Xiao, CHEN Lijun. Experimental Investigation of Parachute in Different Breathability[J]. Acta Aerodynamica Sinica, 2008, 26(1):19-25. (in Chinese)
Numerical Simulation of Steady-state Descent Phase of Parachute Based on SPH Method
YAO Xiangru YU Li WU Qiong
(College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
With the rise of computer technology and numerical simulation, it is possible to describe accurately the dynamic chatacteristics of parachute. In order to eliminate the influence of negative volume due to large mesh deformation in the traditional parachute simulation, this article uses Smoothed Particle Hydrodynamics (SPH) method. The steady-state descent phase of parachute is numerically simulated, and the aerodynamic coefficients are consistent with wind tunnel test results. The influence of air particle density on the numerical results is investigated. It turns out that an effective coupling of the parachute structure with the flow field is difficult to be achieved in low particle density condition, which reduces the calculation accuracy. However, when the particle density exceeds a certain value, the computational consumption will increase and the calculation accuracy will be affected because of the rounding error. Therefore, the optimal particle number is determined. On this basis, the descent processes of parachute with different initial velocities are simulated. The dynamic change of the canopy shape, the projected diameter, the drop speed, the aerodynamic force and the swinging angle are obtained. It is found that the velocity has less impact on the parachute breath rate, the balancing speed as well as the aerodynamic force. The canopy breath amplitude and the swinging angle increase as the velocity increase, and the attenuation property of swinging angle is lower than the project diameter. SPH method can effectively avoid large grid deformation problems in the aspect of parachute fluid-structure interaction and has wide application prospects in the field of large deformation on flexible fabric with fluid-structure interaction method.
descent process; fluid-structure interaction; smoothed particle hydrodynamics method; parachute
(编辑:刘颖)
V244.21
A
1009-8518(2016)03-0048-07
10.3969/j.issn.1009-8518.2016.03.006
姚向茹,女,1992年生,南京航空航天大学航空宇航学院硕士生。研究方向为飞行器救生及生命保障,回收系统动力学。E-mail:15150678158@163.com。
2015-11-17
国家自然科学基金(11172137)资助项目;江苏高校优势学科建设工程资助项目(PAPD);南京航空航天大学研究生创新基地(实验室)开放基金资助(kfjj20150104-01);中央高校基本科研业务费专项资金资助

