信息密度评价采样成像系统的合理性分析

贺金平阮宁娟刘兆军刘雨晨庄绪霞



信息密度评价采样成像系统的合理性分析

贺金平阮宁娟刘兆军刘雨晨庄绪霞

（北京空间机电研究所，北京 100094）

针对信息密度评价采样成像系统性能理论依据不足的问题，文章提出通过对不同成像系统的信息密度和所成图像的质量评价参量进行一致性分析，来研究信息密度评价采样成像系统性能的合理性。信息密度是融合了系统调制传递函数、信噪比和混叠的综合成像质量表征参量，文章对成像系统的信息密度计算式进行了推导，在此基础上介绍了计算信息密度所需各分量的数学模型，进而对仿真流程进行了描述。仿真实验结果表明，成像系统信息密度值随着成像系统设计参量数值的变大而不断增加，计算得到的图像质量评价参量也呈现了相同的规律，信息密度与图像质量评价参量之间保持了较好的单调一致性。调整成像系统参数进行物理验证实验，实验结果进一步证明了利用信息密度评价采样成像系统性能的合理性。

信息密度 混叠失真 系统评价 成像质量表征 图像熵 航天遥感

0 引言

传统上采样成像系统性能主要通过系统信噪比和奈奎斯特频率处的系统调制传递函数（MTF）进行评价。然而，MTF只反映了系统的幅频响应情况，表征了图像的模糊失真，信噪比则只表征了图像的噪声失真程度，不能表征由于欠采样而产生的混叠失真[1-3]，表征成像系统性能不全面。要准确度量整个成像系统的性能，应从系统工程角度出发进行讨论。系统的整体性能主要由其组成成分之间及其与环境之间的相互作用产生，系统内部各要素之间及其与环境之间的相互作用方式多种多样，可概括为物质、能量和信息的联系方式。成像系统包括光学系统和电子学系统，实质上两个系统传递的都是信息，基于信息论的量度对光电成像的物体和图像能做出更为科学、精细、定量的描述。

目前国际上已出现利用信息理论评价成像系统性能的研究，比如美国的NASA，最活跃的研究群体是以Huck为代表的研究组。文献[4]提出了一种描述光机线扫描成像过程的信息密度表达，进而分别讨论了系统的最大信息密度随系统频率响应形状、信噪比和量化位数的变化规律；文献[5]在成像过程加入了图像处理环节，并对成像系统信息密度进行了重新推导，分析了采样间距、量化噪声、增益等对信息密度的影响；文献[6]提出信息、保真度、优化的维纳复原公式解释了欠采样效果—混叠，得到的结论为：不同的图像形成算法倾向于不同的光学设计，信息优化设计最大化了图像复原的鲁棒性，将信息优化设计与3×3横向抑制的像平面处理算法结合到一起，得到了可估算人类视觉边缘响应的空域响应波形；文献[7]讨论了信息、保真度、编码数据熵和真实复原图像质量之间的关系；文献[8]利用信息密度优化设计高光谱成像系统，从而获得最优的谱段数量；文献[9]利用信息密度优化扩展景深成像系统；文献[10-12]研究了利用信息论评价和优化采样成像系统；文献[13]提出了基于信息理论的航天相机性能评价方法。

本文对成像后的信息密度计算公式进行了推导，在此基础上介绍了计算信息密度的各表征参量模型，进而对图像仿真流程进行了描述。通过图像仿真获取不同图像质量评价参数值，对计算出的信息密度数值进行一致性分析。针对信息密度评价采样成像系统性能理论依据不足的问题，本文提出通过对相同成像条件下对应不同系统设计参数的信息密度和所成图像的质量评价参量进行一致性分析，仿真实验结果证明信息密度可以用于评价采样成像系统性能。

1 信息密度

将成像系统视为通信信道，景物的光强分布是信源，图像形成过程中的退化代表着信息在信道中的丢失，最后获取的图像是信宿。图像采集的过程可以看作信源在信道中的有损传输。系统设计目标可以归结为设计最好的信道，使景物和图像之间的互信息量最大。

由于图像的大小是有限的，因此图像的空间范围称为图像空间支持域，互信息量依存于图像空间支持域。相同空间支持域上的信息量使不同成像系统的性能具有可比性，因此，引入单位空域面积上的信息量（即信息密度）作为目标函数，则

式中为信息密度；为平均互信息量；为单位空间面积上成像图像中所保留原始景物的信息量，且，其中，和为采样间隔，和为采样次数。

由于熵与功率谱密度相关，因此可以在描述图像采集和处理的功率谱密度模型基础上，根据信息论中信息量及信息密度的定义，推导信息密度计算公式。图像采集和处理模型如图1所示。

图1 像采集和处理模型

成像过程的傅里叶变换为

由式（4）可以分解式（6）为

由于式（8）右侧分量为独立的不相关量，则式（8）对应的功率谱密度等式为

其中，

由功率谱密度定义可知，

式（10）中，由于白噪声是独立不相关的，其对应的傅里叶域的功率谱密度的面积积分值为功率谱密度自身，因此有：和。

那么，由式（9）和（12）可得成像系统的输出信息量为

则信息密度为

由式（10）可将式（14）转换为

由式（15）可知，信息密度函数是融合了调制传递函数、信噪比、边带混叠等多种参数的综合性成像质量表征参量，涵盖了在轨成像链路中场景、大气、遥感器、卫星平台等各个环节对像质的影响过程。

2 计算信息密度的各分量数学模型

2.1 系统调制传递函数模型

目前在轨成像系统MTF可简化为光学系统MTF（MTFopt）、探测器MTF（MTFsen）和卫星平台运动MTF（MTFmov）三部分，即

MTFopt模型结构复杂，本文采用法国国家太空研究中心（CNES）所用的MTFopt模型，为

定义为探测器采样频率和MTFopt截止频率的比值，其中为相邻探测器像元的中心距离。为光学系统点扩散函数的表征，那么系统设计参数可以理解为探测器对衍射受限光学系统点扩散函数采样好坏的一个量度标准。因此的取值问题实质上是在直径为2.44的光学衍射斑中设计多少个探测器像元的问题[14-15]。设，则上述模型可写为

可以认为探测器的每个像元空域形状函数为探测器点扩散函数，MTFsen可由探测器的每个像元空域形状函数的傅里叶变换求得。探测器的单个像元可以看作是理想的二维矩形函数。一维矩形函数为

式中为自变量；为矩形函数的窗口大小。一维矩形信号的傅里叶变换（sinc函数）为

=1时的二维sinc函数等值线如图2所示，奈奎斯特频率在0.5，第一个过零点在±1，在奈奎斯特频率处最小的归一化MTF数值为0.4，奈奎斯特频率以外的能量仍然较多。

卫星平台的运动可以看作匀速直线运动，水平方向线性移动可用矩形函数表示为

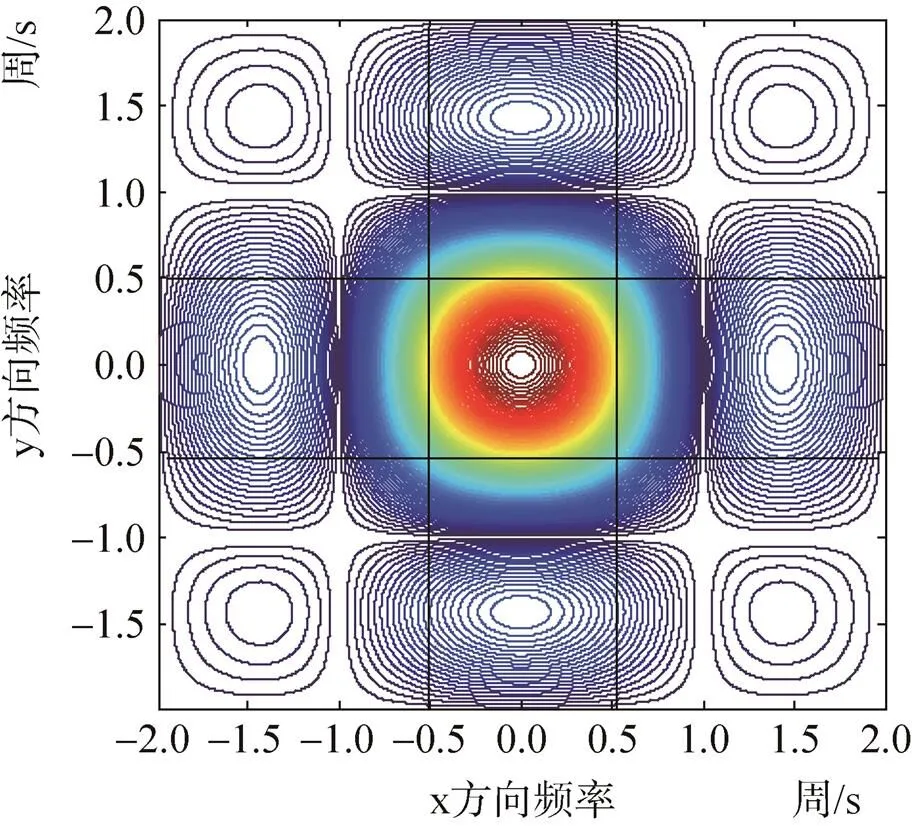
图2 探测器MTF等值线

MTFmov模型为上述空域点扩散函数的傅里叶变化为

则MTFmov的计算式为

2.2 信噪比模型

成像系统的信噪比一般定义为：在一定光照条件下，成像系统输出信号和随机噪声均方根电压的比值，即

a) 量化是均匀的；

c) 采样信号的量化误差与任一采样信号是不相关的。

则有

2.3 辐射场景量化表征模型

辐射场景量化表征模型有多种形式[16-18]，本文采用高斯—马尔科夫模型，该模型为基于信号能量分布特性的功率谱密度表征模型，广泛应用于机器视觉性能模型建模分析中。

假设辐射场景是幅度上服从高斯分布、宽度上服从泊松分布的二维随机过程，并假定两者相互独立，最终推导出功率谱密度服从下面的形式的二维马尔科夫过程：

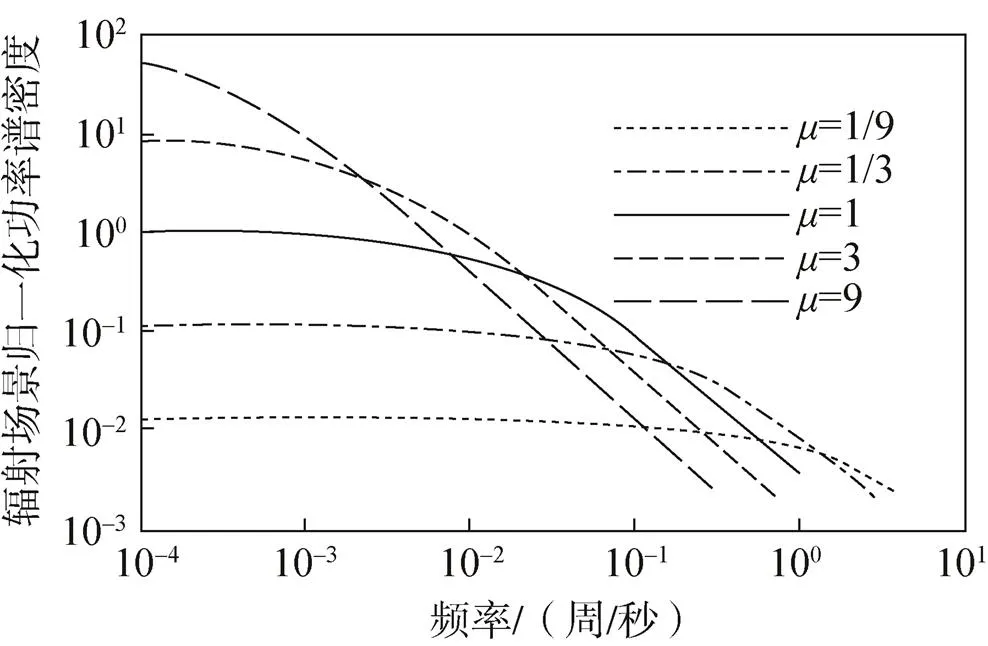
图3 辐射场景归一化功率谱密度分布图

综上所述，通过将上述的辐射场景模型、系统MTF模型、信噪比模型等代入到信息密度的计算公式（15）中，如图4所示，可以对采样成像系统的信息密度进行求解。

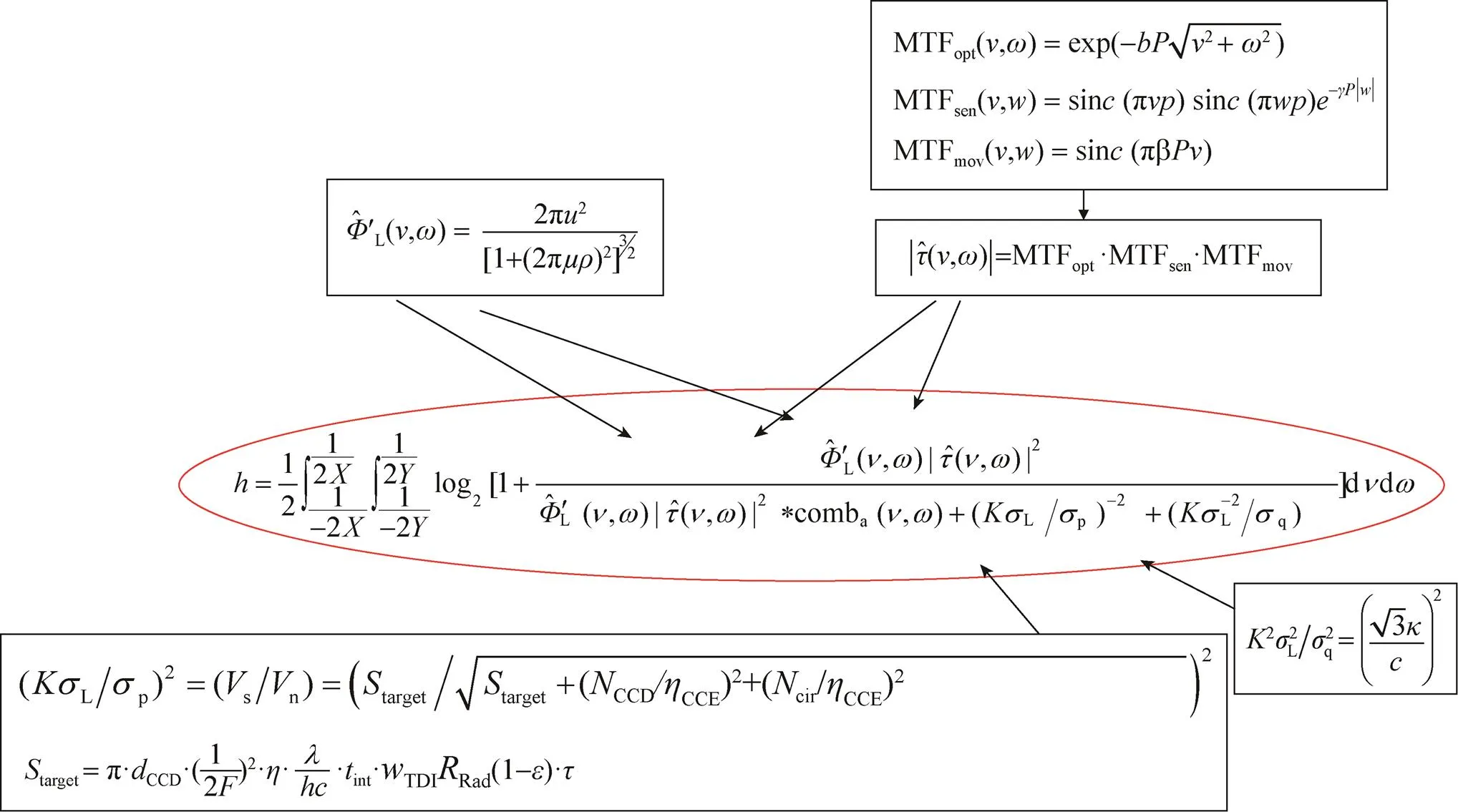
图4 信息密度模型计算示意图

3 实验验证与分析

取光信号转化为电信号增益系数=1，设计了两个成像系统观察相同的场景。系统1设计为，，。系统2设计为=1，，。由公式计算出系统1的信息密度bit/μm2，系统2的信息密度bit/μm2。

选取了1 000×1 000像素的泰国机场遥感图像作为原始图像，输出图像为500×500像素，按照如图5所示的流程进行仿真。MTF模型如上所述，由于信息密度推导过程中含有图像处理的过程，因此，信息密度的数值表征的是经图像复原后的统计信息。

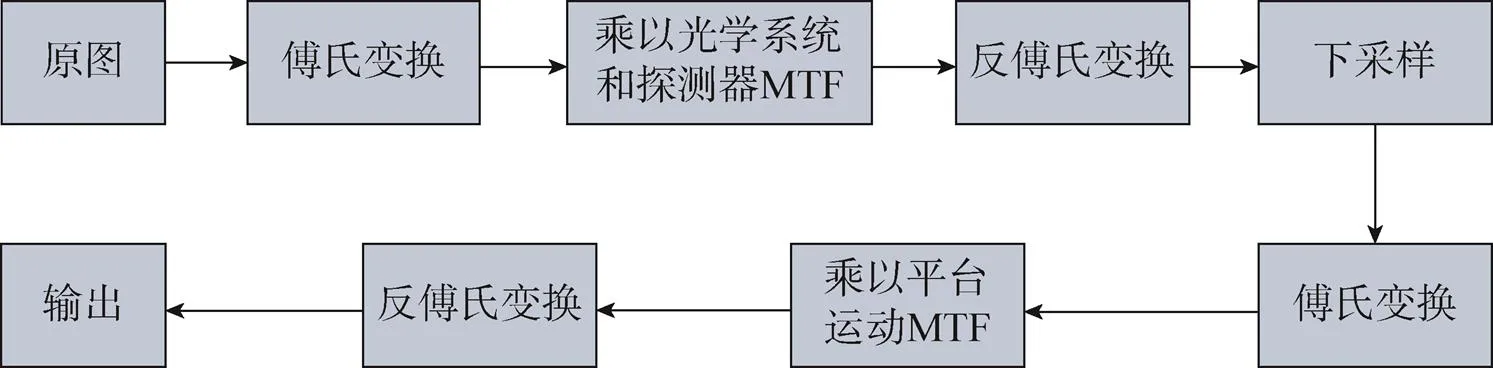
图5 图像仿真流程

本文设计了7个不同的成像系统，7个系统的不同在于/数值逐渐增大，通过上面的参数值设置及模型可以计算出信息密度的数值。随着/数值的增大，信息密度也逐渐增大。通过降质下采样仿真得到7个系统对应的输出图像，对输出图像进行图像复原，进而计算复原后图像的熵和局部对比度计算，计算公式详见[19]。由数值可以看出，图像质量评价参量的数值随着/数值的增大也逐渐增大。信息密度与图像质量评价参量之间的单调一致性关系如图6所示。该实验说明：在一定的约束条件下，/的数值较大更有利于使系统获取更多的有效信息。

表1 不同成像系统的信息密度值与图像质量评价参量值列表

Tab.1 The list of information density and image quality assessment for various imaging systems

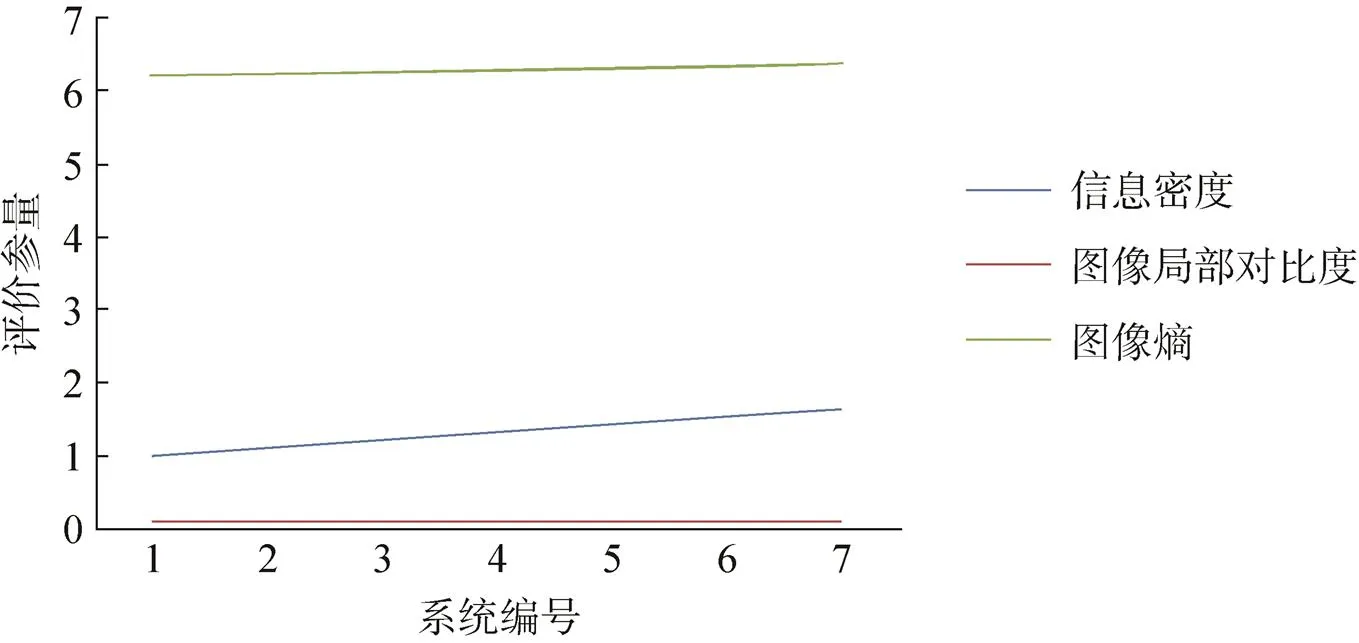
图6 信息密度与图像质量一致性分析图

为了进一步验证信息密度与图像质量的一致性，搭建物理验证实验装置，通过调节数拍摄两种不同/系统对应的图像。如图7所示，图7（a）为=8（/=0.50）所拍摄的靶标图，图7（b）为=16（/=0.73）所拍摄的靶标图。将图7的成像结果进行50人主观判读实验，选择=8系统品质优的人数为0，选择两系统品质相当的人数为3个，选择=16系统品质优的人为47个。由对应的局部放大图图7（c）、（d）也可主观进行对比。

混叠失真在图像中的表现为摩尔条纹、锯齿、断线、高频混成低频等现象，由上述局部图可看出=8系统图像存在严重的混叠失真现象。而这些混叠失真现象在=16系统图像中没有出现。=16的系统图像左上角竖条纹靶标断线得到缓解，线条更连贯；45°和135°斜条纹靶标的锯齿假信息也消失了；右下角横条纹靶标混在一起的条纹也可以区分开。输入物理验证实验系统参数，计算不同系统对应的信息密度数值（相对于仿真实验设计的不同成像系统，物理验证试验系统信噪比较低，对应的信息密度数值也普遍较低）。=8系统对应的信息密度为1.7501 bit/像素，=16系统对应的信息密度为1.8241 bit/像素，与上述主观判读结果一致。物理验证实验结果进一步证明信息密度可以作为评价采样成像系统性能的 指标。

图7 不同λF/P时系统靶标成像图

4 结束语

本文在研究采样成像系统信息密度计算公式的基础上，结合简化后的各分量计算模型，计算了不同系统设计参数的系统信息密度，并利用对应的系统设计参数进行图像仿真，计算输出图像复原后的图像熵和局部对比度，图像质量评价参量与系统信息密度保持了良好的一致性。本文提出的验证信息密度评价采样成像系统合理性方法，还需要进一步增大仿真数据量及引入更多的客观图像质量评价参量，来更客观地分析信息密度与图像质量的相关性问题。

[1] 陈世平, 姜伟. 航天光学采样成像系统MTF的优化设计与MTFC[J]. 航天返回与遥感, 2007, 28(4): 17-22. CHEN Shiping, JIANG Wei. The MTF Optimal Design and MTFC for Spaceborne Optical Sampled imaging System[J]. Spacecraft Recovery & Remote Sensing, 2007, 28(4): 17-22. (in Chinese)

[2] 满益云, 陈世平, 刘兆军, 等. MTFC在光学遥感成像系统优化设计中的应用研究[J]. 航天返回与遥感, 2007, 28(4): 39-47. MAN Yiyun, CHEN Shiping, LIU Zhaojun, et al. Study on MTF Compensation Application to the Optimization Design of Optical Remote Sensing Imaging System[J]. Spacecraft Recovery & Remote Sensing, 2007, 28(4): 39-47. (in Chinese)

[3] 刘兆军, 周峰, 阮宁娟, 等. 一种光学遥感成像系统优化设计新方法研究[J]. 航天返回与遥感, 2011, 32(2): 34-41. LIU ZhaoJun, ZHOU Feng, RUAN Ningjuan, et al. Study on Trade-offs Design Method for Space Optical Remote Sensing Imaging System[J]. Spacecraft Recovery & Remote Sensing, 2011, 32(2): 34-41. (in Chinese)

[4] HUCK F O, PARK S K. Formulation of the Information Capacity of the Optical-mechanical Line-scan Imaging Process[G]. USA: NASA Technical Note, 1975: 1-38.

[5] HUCK F O, HALYO N, PARK S K. Information Efficiency of Line-scan Imaging Mechanisms[J]. Applied Optics, 1981, 20(11): 1990-2007.

[6] HUCK F O, FALES C I, HALYO N, et al. Image Gathering and Processing: Information and Fidelity[J]. Opt. Soc. Am, 1985, 2(10): 1644-1666.

[7] HUCK F O, FALES C I. Information, Entropy, and Fidelity in Visual Communication[J]. SPIE Conference on Visual Information Processing, 1992, 1705: 145-154.

[8] REICHENBACH S E, XIONG Y, NARAYANAN R, et al. Information Theoretic Assessment and Design of Hyperspectral Imaging Systems[J]. SPIE Conference on Visual Information Processing, 1999, 3716: 100-104.

[9] JOESPH V D, GARY W E. Information-optimized Extended Depth-of-field Imaging Systems[J]. SPIE Conference on Visual Information Processing, 2001, 4388: 103-112.

[10] 迟学芬, 石文孝, 韩昌元, 等. 基于信息理论的采样成像系统优化设计方法[J]. 通信学报, 2002, 23(9): 88-93. CHI Xuefen, SHI Wenxiao, HAN Changyuan, et al. Information-theory Based Optimizing Design Methods in Sampled-imaging System[J]. Journal of China Institute of Communications, 2002, 23(9): 88-93. (in Chinese)

[11] 迟学芬, 韩昌元. 基于信息理论的采样成像系统评价方法[J]. 光学精密工程, 2003, 11(2): 104-108. CHI Xuefen, HAN Changyuan. Assessment of Sampled Imaging System Based on Information-theory[J]. Optics and Precision Engineering, 2003, 11(2): 104-108. (in Chinese)

[12] 迟学芬, 韩昌元, 易志栋. 基于信息理论的采样成像系统匹配设计[J]. 光学学报, 2003, 23(3): 278-283. CHI Xuefen, HAN Changyuan, YI Zhidong. Matching Design Methods Based on Information Theory in Sampled Imaging Systems[J]. Acta Optica Sinica, 2003, 23(3): 278-283. (in Chinese)

[13] 陈荣利, 樊学武, 李英才. 基于信息理论的航天相机性能评价研究[J]. 光学技术, 2004, 30(4): 434-436. CHEN Rongli, FAN Xuewu, LI Yingcai. Study on Synthetically Evaluating Image Quality of Aero-cameras[J]. Optical Technique, 2004, 30(4): 434-436. (in Chinese)

[14] BAI H G. Analysis on the Interaction between Image Quality and Optical Q Based on NIIRS for Remote Sensing Systems[J]. Proc. of SPIE, 2011, 8006: 1-6.

[15] PHILIPPE L, LUC D, SEBASTIEN V, et al. ASPIICS: a Giant Coronagraph for the ESA/PROBA-3 Formation Flying Mission[J]. Proc. of SPIE, 2010, 7731: 1-18.

[16] SCHAAF V D, HATEREN J H. Modeling the Power Spectra of Natural Images: Statistics and Information[J]. Vision Research, 1996, 36(17): 2759-2760.

[17] PAMPLONA D, TRIESCH J, ROTHKOPF C A. Power Spectra of the Natural Input to the Visual System[J]. Vision Research, 2013, 83: 66-75.

[18] GEISLER W. Visual Perception and the Statistical Properties of Natural Scenes[J]. Annual Review of Psychology, 2008, 59: 167-192.

[19] HE Jinping, GAO Kun, NI Guoqiang，et al. Learning from Ideal Edge for Image Restoration[J]. IEICE Transactions on Information and Systems, 2013, E96-D(11): 2487-2491.

Rationality Analysis on the Information Density Evaluation for Sampled Imaging System

HE Jinping RUAN Ningjuan LIU Zhaojun LIU Yuchen ZHUANG Xuxia

（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

Considering the deficiency in the theoretical basis about information density evaluating sampled imaging system, this article proposes a method that compares the information density calculated from the different system parameters with the corresponding images’ assessments in order to obtain the rationality analysis on the information density evaluation for sampled imaging system. Information density contains system MTF, SNR and aliasing , and is a comprehensive imaging representation. Firstly, the calculation formula of information density is derived. The useful representation models for calculating the information density are introduced. Then the simulation procedure is described. Experimental results show that under certain conditions, the higher the system designed parameter/is, the higher the information density of imaging system is. And the quality assessments of the corresponding images also become higher. The information density keeps good monotonicity with image quality assessments. Physical verification experiment is implemented through adjusting the system parameters. Experimental results further prove the rationality of using information density to assess the sampled imaging system.

information density; aliasing; system evaluation; imaging quality representation; image entropy; space remote sensing

（编辑：毛建杰）

O438

A

1009-8518(2016)03-0100-11

10.3969/j.issn.1009-8518.2016.03.012

贺金平，女，1981年生，2009年获得北京理工大学光学工程专业博士学位，高级工程师。研究方向为采样成像系统的优化设计方法和新型光学遥感成像系统、图像复原方法及像质评价方法等。E-mail：30212046@qq.com

2015-10-14

国家重点基础研究发展计划项目(973项目)(613210)