高分辨率光学遥感卫星几何链路定位精度分析

夏中秋黄巧林何红艳伏瑞敏岳春宇



高分辨率光学遥感卫星几何链路定位精度分析

夏中秋黄巧林何红艳伏瑞敏岳春宇

（北京空间机电研究所，北京100094）

为了提高高分辨率光学遥感卫星无控制点定位精度，针对如何进行定位精度指标分配的问题，介绍了高分辨率光学遥感卫星几何链路的概念，分析了几何链路中各环节的系统误差和随机误差，采用双线阵相机立体定位方式推导了定位精度计算方法，得出了高程精度的主要影响因素，并以满足 1∶10 000测图比例尺要求为例，进行了定位精度指标分析，提出了提高定位精度的措施。结果表明，主距误差对高程精度影响极小，可忽略不计；卫星姿态角误差是高程精度的主要影响因素，其中俯仰角误差的影响最大；姿态角测量与确定精度达到0.4″、星敏与相机间夹角稳定性精度达到0.1″，可使相对高程精度达到1.497m，满足相对高程精度要求。利用几何链路分析定位精度的方法可用于高分辨率光学遥感卫星定位精度指标分配。

几何链路 高程精度 指标分配 光学遥感 高分辨率卫星

0 引言

近年来国内外多颗高分辨率光学遥感卫星在对地目标观测领域得到了广泛应用[1-2]。利用成像链路仿真进行高分辨率光学遥感卫星设计，已逐渐成为国内外研究的热点。成像链路仿真主要包括辐射链路仿真和几何链路仿真两个方面。国内外围绕成像链路仿真已展开大量工作，例如文献[3]对数字相机成像链路进行了建模，将成像链路仿真分为辐射传输、系统成像、图像处理、显示和解译五个步骤；文献[4]对高光谱遥感系统进行了端到端的仿真，将成像链路仿真分为光线追迹、辐射传输和光电信号处理三个模块，其中光线追迹用于确定地面点在图像上的位置；文献[5]对空间光学系统进行了全链路仿真，将成像链路分为信号链路、传递链路和噪声链路，分别建立了调制传递函数模型和信噪比模型。这些仿真的共同点是更侧重于辐射链路的仿真，几何链路的仿真还处于初级阶段，辐射链路主要应用于图像品质分析，而几何链路的应用主要体现在定位精度分析，因此利用几何链路仿真进行定位精度分析是本文研究的重点。

许多关于定位精度的研究利用不同的参数构建模型[6-9]，分析了无地面控制点卫星摄影测量的技术难点[10]。从误差传播的角度出发，文献[11]利用星敏感器精度、GPS精度、图像成像时间精度以及相机内方位元素精度的假设值，估算了推扫式成像的定位精度；文献[12]分析了基线测量、摄站位置、姿态角、主点和主距等随机误差的影响；文献[13–14]分析了内方位元素误差和外方位元素误差等随机误差的影响；文献[15]利用星地全链路误差仿真与评估数学模型进行了定量分析。这些研究工作的共同点是大多以卫星摄影测量中的参数进行讨论，且仅考虑了各参数的随机误差，较少涉及高分辨率光学遥感卫星总体设计中影响定位精度的各个指标，在实际设计中，这些指标不仅存在着随机误差，还存在着系统误差，例如文献[16]通过试验验证了姿态角常差的存在并进行了姿态角常差检校，在此基础上进行了系统误差检校[17]。因此，结合高分辨率光学遥感卫星成像特点，综合分析影响定位精度的各个指标的随机误差和系统误差，是本文的研究思路。

本文介绍了高分辨率光学遥感卫星几何链路的概念，将几何链路仿真用于卫星各环节指标设计与分析，以提高定位精度。针对双线阵相机，根据无控制点立体图像定位的原理，首先分析了由遥感器和卫星平台引起的影响定位精度的系统误差和随机误差，得出高程精度的主要影响因素，以1∶10 000测图比例尺为例，在满足相对高程精度要求条件下进行指标分配，最后提出了提高高分辨率光学遥感卫星定位精度的措施。

1 高分辨率光学遥感卫星几何链路

1.1 几何链路组成

高分辨率光学遥感卫星几何链路的构建主要涉及观测目标（地形起伏、地球曲率）、大气折射、遥感器（光学系统、探测器）、卫星平台（轨道、姿态）、地面处理、精度评价等方面，还应考虑由于采用大口径、长焦距的光学系统引起的稳定性问题和卫星轨道姿态的稳定性问题，其中影响定位精度的各项指标是高分辨率光学遥感卫星立体定位中的主要研究对象。

几何链路中影响定位精度的各项指标与定位精度的误差来源相对应，主要包括三个方面。

在遥感器方面，定位精度误差来源于主点、主距和畸变，主要包括：1）相机研制过程中对主点、主距和畸变进行精确测量时，受标定仪器精度影响会产生一定的测量误差；2）在轨运行中力、热环境会导致相机光轴、主距、光学镜头面形及位置发生变化，从而引起主点稳定性、主距稳定性及畸变稳定性误差。

在卫星平台方面，定位精度误差来源于卫星的轨道和姿态，主要包括：1）卫星轨道位置坐标确定中存在定轨误差；2）姿态测量与确定过程中受姿态敏感器硬件精度和姿态确定算法影响，存在姿态测量误差和姿态确定误差；3）星敏与相机间夹角存在标定误差；4）在轨运行中力、热环境导致星敏与相机间夹角发生变化，引起星敏与相机间夹角稳定性误差；5）两次姿态数据之间卫星指向会发生漂移，引起卫星姿态稳定性误差；6）卫星高频振动引起的卫星姿态稳定性误差。

在时间同步方面，时间同步精度会通过轨道参数和姿态稳定度影响定轨精度和定姿精度，进而对定位精度产生影响。

1.2 基于几何链路的定位精度算法

高分辨率光学遥感卫星立体定位地面点坐标计算方法如下

式中、、为地面点坐标；X1、Y1、Z1和X2、Y2、Z2为前后相机摄站位置坐标；B、B、B分别为摄影基线分量；1和2分别为前后相机的点投影系数；1、1、1和2、2、2分别为前后相机的像空间辅助坐标。与传统计算方法不同，本文考虑了镜头畸变的测量误差及其稳定性的影响，则像空间辅助坐标的计算方法为

式中01和02分别为前后相机的主点；1和2分别为前后相机的主距；1和2分别为前后相机的镜头畸变；11、11、11、12、12、12、13、13、13为方向余弦，由前视相机的俯仰角1、翻滚角1、偏航角1确定，21、21、21、22、22、22、23、23、23为方向余弦，由后视相机的俯仰角2、翻滚角2、偏航角2确定。

以前视相机为例，根据多元非线性函数误差估计理论，首先求解各误差传播系数，即地面点坐标、、分别对01、1、1、X1、Y1、Z1、1、1、1的偏导数，误差传播系数的大小体现了相对高程精度受某个指标的影响程度，然后结合高分辨率光学遥感卫星设计中各影响定位精度的指标，计算得出定位精度，具体方法为

式中σ为定轨精度；σ为时间同步精度σ与轨道速度结合引起的飞行方向上的轨道位置精度，

卫星姿态的系统误差ε、ε、ε及卫星姿态的稳定性精度σ、σ、σ的计算公式为

式中ε2为星敏与相机间夹角的系统误差；σ1为姿态测量与确定精度；σ2为星敏与相机间夹角稳定性精度；σ3为姿态稳定度引起的卫星姿态稳定性精度，，其中，为卫星姿态稳定度，为星敏两次定姿之间的时间间隔；σ4为卫星高频振动引起的卫星姿态稳定性精度；σ为时间同步精度与姿态稳定度结合引起的卫星姿态稳定性精度，。

传统的立体定位精度计算方法从摄影测量的角度出发，以摄影基线误差、摄站坐标误差、姿态角误差、像点量测误差及主距误差为参数，分析各参数随机误差的影响。几何链路定位精度计算方法从高分辨率光学遥感卫星设计角度出发，以镜头畸变、主点、主距的测量误差，摄站精度，星敏感器测量与确定精度，星敏感器与相机间夹角间标定误差和稳定性精度，卫星姿态稳定度，卫星高频振动引起的姿态角精度和时间同步精度为参数，综合分析了各参数系统误差和随机误差两个方面的影响，在一定意义上体现了制造要求和稳定性要求，因此更适用于定位精度指标分配。

2 定位精度指标分析

明确影响定位精度的主要因素，是进行几何链路定位精度指标分配的前提。本节利用基于几何链路的定位精度算法，得出各项误差传播系数，通过误差传播系数的大小判别几何链路中各误差对定位精度的影响程度，以期得出定位精度的主要影响因素。

设定线阵像元数为20 000、轨道高度为500km、像元尺寸为10μm、主距为15m。主点、主距和畸变误差传播系数如图1所示，主点与畸变误差传播系数相同，主距误差与主点和畸变误差相比对高程精度的影响较大，误差传播系数数量级为10–12，在前、后视相机光轴与正视方向夹角为45°时，主距误差影响达到最低。轨道位置坐标误差传播系数如图2所示，可以看出在前、后视相机光轴与正视方向夹角较小时，沿轨方向投影中心位置坐标误差影响较大，且随着前、后视相机光轴与正视方向夹角增大影响逐渐降低。卫星姿态误差传播系数如图3所示，可看出卫星俯仰角和偏航角对高程精度的影响变化趋势相近，但误差传播系数的数量级不同，在前、后视相机光轴与正视方向夹角为45°时，俯仰角误差、翻滚角误差和偏航角误差的影响达到最低。

图1 主点、主距和畸变误差传播系数

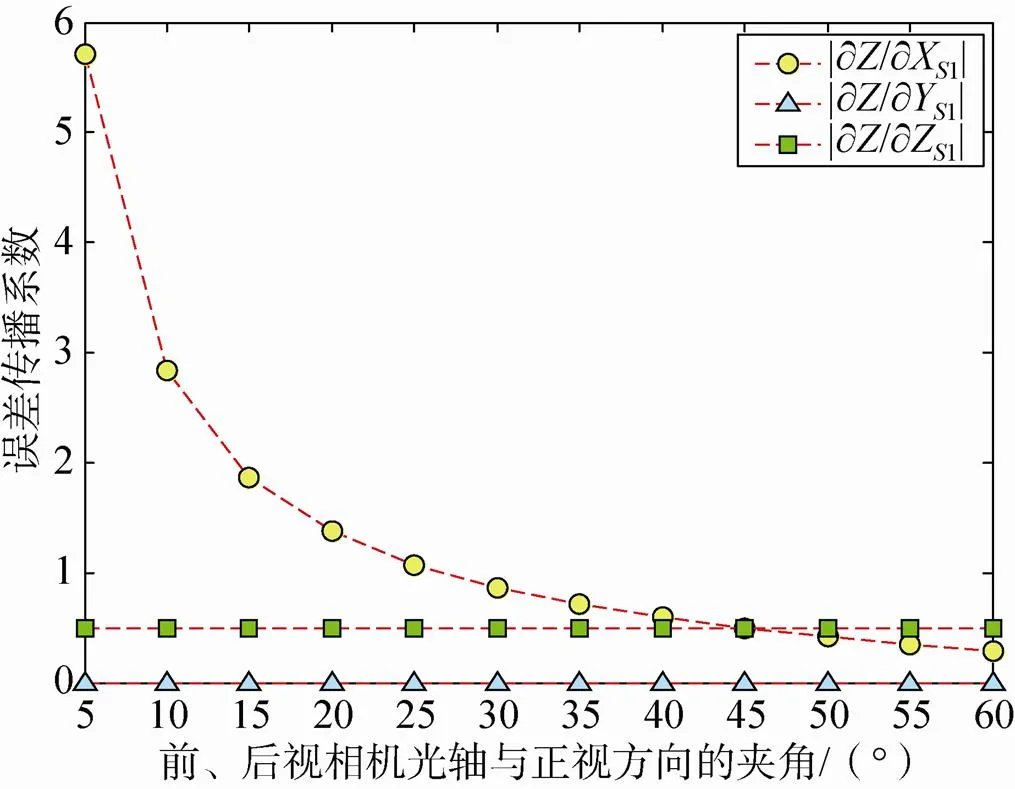
图2 轨道位置坐标误差传播系数

图3 卫星姿态角误差传播系数

总体而言，前、后视相机光轴与正视方向的夹角取值不同时，即采用不同的基高比条件下，俯仰角误差传播系数和偏航角误差传播系数远大于主点、主距、畸变误差传播系数和轨道坐标误差传播系数，且在描述卫星姿态的三个姿态角中俯仰角误差传播系数最大，说明俯仰角误差对高程精度的影响最大，因此在分析提高定位精度的措施时，应重点考虑提高卫星姿态精度。

3 提高定位精度的措施

目前，几何链路中影响定位精度的各指标精度已达到的水平如表1所示[19-20]。根据基于几何链路的定位精度算法，选取前、后视相机与正视方向夹角为25°，消除主点测量误差、主距测量误差、畸变测量误差、星敏与相机间夹角标定误差后，卫星能达到的相对高程精度为3.07m，不能满足1∶10 000测图比例尺要求。根据相对高程精度的计算公式[18]

式中h为相对高程精度；l为等高距。若l为5m，相对高程精度应达到1.5m，为了满足1∶10 000测图比例尺要求，还需提高影响定位精度的各指标精度。

表1 几何链路中各指标精度

Tab.1 Accuracy of each index in geometric chain

在定位精度指标分析中，可知主距误差对相对高程精度的影响极小，可忽略不计，在轨道精度和姿态精度中，约束定位精度的关键在于卫星的姿态精度。据前文定位精度算法，得出由姿态稳定度引起的姿态稳定性精度为0.225″，和姿态测量及确定精度、星敏与相机间夹角稳定性精度量级相同，大于高频振动引起的卫星姿态稳定性精度，因此提高卫星姿态精度，可主要从姿态测量与确定精度、星敏与相机间夹角稳定性精度、卫星姿态稳定度三个方面考虑。仅改变卫星姿态测量与确定精度，对相对高程精度的影响如图4所示；仅改变星敏与相机间夹角稳定性精度对相对高程精度的影响如图5所示；仅改变卫星姿态稳定度对相对高程精度的影响如图6所示。

由图4~6可知，仅提高某一项指标的精度仍无法满足1∶10 000测图比例尺相对高程精度要求，所以需要进一步考虑提高两项指标精度。为了在技术上较易实现，本文采取的方法为：保持卫星姿态稳定度不变，交替提高σ1和σ2两项指标，以提高相对高程精度。卫星姿态测量与确定精度、星敏与相机间夹角稳定性精度取值不同条件下，相对高程精度变化列于表2中。可知当卫星姿态测量与确定精度达到0.4″、星敏与相机间夹角稳定性精度达到0.1″时，相对高程精度达到1.497m，符合1∶10 000测图比例尺相对高程精度要求。

图4 卫星姿态测量与确定精度对相对高程精度的影响

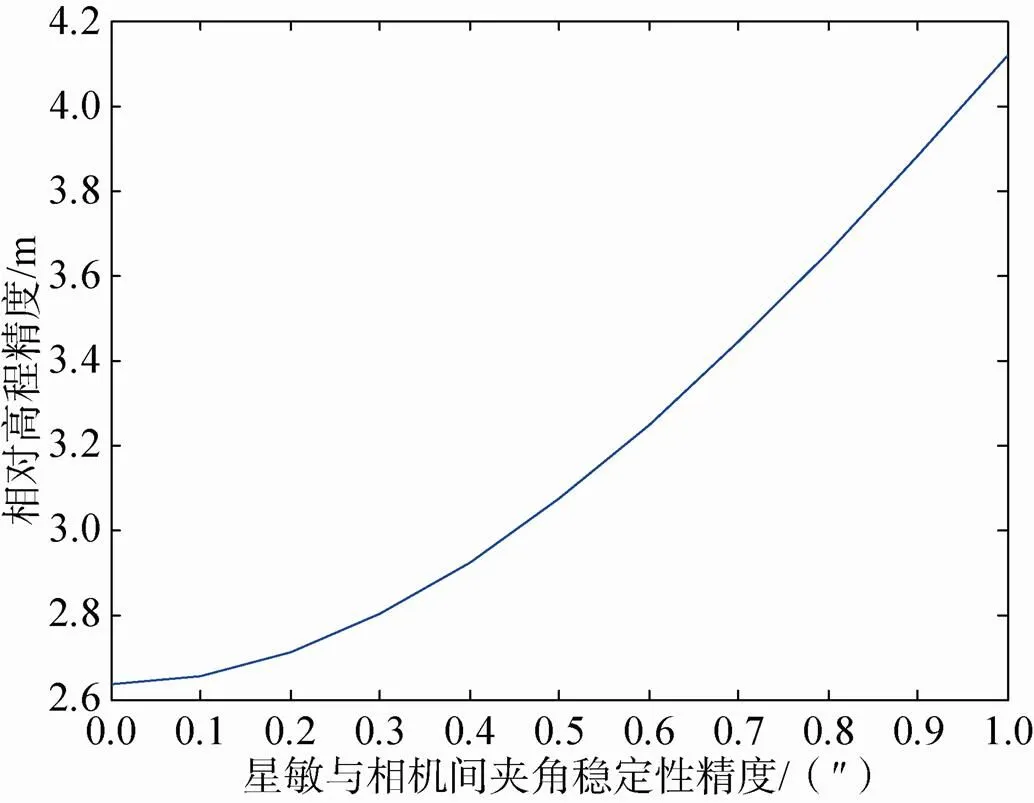
图5 星敏与相机间夹角稳定性精度对相对高程精度的影响

图6 卫星姿态稳定度对相对高程精度的影响

表2σ1和σ2不同取值条件下的相对高程精度

为了提高卫星姿态测量与确定精度σ1和星敏与相机间夹角稳定性精度σ2这两项指标，使相对高程精度满足1∶10 000测图比例尺要求，可采取如下措施：1）用高精度星敏感器作为主要姿态测量敏感器，将姿态测量数据和高精度陀螺数据下传，并提高星敏数据和陀螺数据的输出频率，由地面确定算法解算卫星姿态，以保证卫星姿态测量的连续性和卫星姿态确定的准确性；2）支架选用低膨胀复合材料，星敏与相机采用一体化和等温化的设计，以减小由温差引起的星敏光轴指向与相机光轴指向的相对随机变化。

4 结束语

本文介绍了高分辨率光学遥感卫星几何链路的概念，引入了几何链路中各环节的随机误差和系统误差，以1∶10 000测图比例尺为例，进行了定位精度指标分析，并针对主要环节提出相应措施。根据文中所取参数，得出以下结论：

1）主距误差对高程精度的影响极小，可忽略不计，前、后视相机光轴与正视方向夹角为45°时，可使主距误差传播系数为0。

2）轨道位置坐标误差对高程精度的影响远小于俯仰角误差、偏航角误差对高程精度的影响，沿轨方向轨道位置坐标误差传播系数随基高比增大而逐渐降低。

3）卫星姿态角误差是高程精度的主要影响因素，其中俯仰角误差的影响最大，前、后视相机光轴与正视方向夹角为45°时，可使俯仰角误差传播系数达到最小。

4）为提高相对高程精度，需提高卫星姿态测量与确定精度、星敏与相机间夹角稳定性精度两项指标的精度，当卫星姿态测量与确定精度达到0.4″、星敏与相机间夹角稳定性精度达到0.1″时，相对高程精度可达到1.497m，满足1∶10 000测图比例尺要求。

[1] 黄巧林, 姜伟. 高分辨率航天光学遥感器发展新思路研究[J]. 航天返回与遥感, 2007, 28(4): 48-50. HUANG Qiaolin, JIANG Wei. A Study of the New Direction of Space-borne Hi-resolution Optical Remote Sensor[J]. Spacecraft Recovery & Remote Sensing, 2007, 28(4): 48-50. (in Chinese)

[2] 唐新明, 谢俊峰, 张过. 测绘卫星技术总体发展和现状[J]. 航天返回与遥感, 2012, 33(3): 17-24. TANG Xinming, XIE Junfeng, ZHANG Guo. Development and Status of Mapping Satellite Technology[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(3): 17-24. (in Chinese)

[3] FIETE R D. Modeling the Imaging Chain of Digital Cameras[M]. Bellingham: SPIE Optical Engineering Press, 1997.

[4] BÖRNER A, WIEST L, KELLER P, et al. SENSOR: A Tool for the Simulation of Hyperspectral Remote Sensing Systems[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2001, 55(1), 299-312.

[5] 阮宁娟, 庄绪霞, 李妥妥, 等. 空间光学遥感系统全链路仿真与分析[J]. 航天返回与遥感, 2013, 34(6): 36-43. RUAN Ningjuan, ZHUANG Xuxia, LI Tuotuo, et al. End to End Simulation and Analysis of Space Optical Remote Sensing System[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(6): 36-43. (in Chinese)

[6] TOUTIN T. Geometric Processing of Remote Sensing Images: Models Algorithm and Methods[J]. International Journal of Remote Sensing, 2004, 25(10), 1893-1924.

[7] WESTIN T. Precision Rectification of Spot Imagery[J]. Photogrammetric Engineering and Remote Sensing, 1990, 56(2), 247-253.

[8] 张过, 袁修孝, 李德仁. 基于偏置矩阵的卫星遥感影像系统误差补偿[J]. 辽宁工程技术大学学报, 2007, 26(4): 517-519. ZHANG Guo, YUAN Xiuxiao, LI Deren. Redressing System Error in Satellite Image based on Bias Matrix[J]. Journal of Liaoning Technical University, 2007, 26(4): 517-519. (in Chinese)

[9] 王任享, 胡莘, 杨俊峰, 等. 卫星摄影测量LMCCD相机的建议[J]. 测绘学报, 2004, 33(2): 116-120. WANG Renxiang, HU Xin, YANG Junfeng, et al. Proposal to Use LMCCD Camera for Satellite Photogrammetry[J]. Acta Geodaetica et Cartographica Sinica, 2004, 32(2): 116-120. (in Chinese)

[10] 王任享, 胡莘. 无地面控制点卫星摄影测量的技术难点[J]. 测绘科学, 2004, 29(3): 3-5. WANG Renxiang, HU Xin. The Difficult Problem about Satellite Photogrammetry without Control Points[J]. Science of Surveying and Mapping, 2004, 29(3): 3-5. (in Chinese)

[11] Bettemir O H. Prediction of georeferencing precision of pushbroom scanner images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(3), 831-838.

[12] 胡莘, 曹喜滨. 三线阵立体测绘卫星的测绘精度分析[J]. 哈尔滨工业大学学报, 2008, 40(5): 695-699. HU Xin, CAO Xibin. Analysis on Precision of Stereo Mapping Microsatellite Using Three-line Array CCD Images[J]. Journal of Harbin Institute of Technology, 2008, 40(5): 695-699. (in Chinese)

[13] 余俊鹏, 孙世君. 测绘相机内方位元素在对地定位中的误差传播[J]. 航天返回与遥感, 2010, 31(2): 16-22. YU Junpeng, SUN Shijun. Error Propagation of Interior Orientation Elements of Surveying Camera in Ground Positioning[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(2): 16-22. (in Chinese)

[14] 余俊鹏, 孙世君, 毛建杰. 卫星遥感影像外方位元素的误差传播研究[J]. 航天返回与遥感, 2011, 32(1): 18-23. YU Junpeng, SUN Shijun, MAO Jianjie. Study on Error Propagation of Exterior Orientation Elements of Satellite Remote Sensing Imagery[J]. Spacecraft Recovery & Remote Sensing, 2011, 32(1): 18-23. (in Chinese)

[15] 王新义, 高连义, 尹明, 等. 传输型立体测绘卫星定位误差分析与评估[J]. 测绘科学技术学报, 2012, 29(6): 427-434. WANG Xinyi, GAO Lianyi, YIN Ming, et al. Analysis and Evaluation of Position Error of Transmission Stereo Mapping Satellite[J]. Journal of Geomatics Science and Technology, 2012, 29(6): 427-434. (in Chinese)

[16] 袁修孝, 余俊鹏. 高分辨率卫星遥感影像的姿态角常差检校[J]. 测绘学报, 2008, 37(1): 36-41. YUAN Xiuxiao, YU Junpeng. Calibration of Constant Angular Error for High Resolution Remotely Sensed Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 36-41. (in Chinese)

[17] 袁修孝, 余俊鹏. 高分辨率卫星遥感影像姿态角系统误差检校[J]. 测绘学报, 2012, 41(3): 385-392. YUAN Xiuxiao, YU Junpeng. Calibration of Angular Systematic Errors for High Resolution Satellite Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 385-392. (in Chinese)

[18] LIGHT D L. Characteristics of Remote Sensors for Mapping and Earth Science Applications[J]. Photogrammetric Engineering & Remote Sensing, 1990, 56(12): 1613-1623.

[19] 金涛, 李贞, 李婷, 等. 提高光学遥感卫星图像几何精度总体设计分析[J]. 宇航学报, 2013, 34(8): 1160-1165. JIN Tao, LI Zhen, LI Ting, et al. System Design and Analysis for Improving Geometric Accuracy of High-resolution Optical Remote Sensing Satellite Image[J]. Journal of Astronautics, 2013, 34(8): 1160-1165. (in Chinese)

[20] 曹海翊, 刘希刚, 李少辉, 等. “资源三号”卫星遥感技术[J]. 航天返回与遥感, 2012, 33(3): 7-16. CAO Haiyi, LIU Xigang, LI Shaohui, et al. ZY-3 Satellite Remote Sensing Technology[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(3): 7-16. (in Chinese)

Analysis of Geolocation Accuracy of High Resolution Optical Remote Sensing Satellite Geometric Chain

XIA Zhongqiu HUANG Qiaolin HE Hongyan FU Ruimin YUE Chunyu

（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

To improve the geolocation accuracy of high resolution optical remote sensing satellite without ground control points in view of the index assignment, a conception of geometric chain is introduced and stochastic error and systematic error are analyzed. Based on the stereo geolocation method, the geolocation accuracy algorithm is derived and the main influencing factor on height accuracy is obtained. Taking the map scale of 1∶10 000 as an example, the value of index is analyzed and the method of increasing geolocation accuracy is put forward. The result is that the focal length error has minimal impact which can be ignored and the attitude error is the main influencing factor which is mainly shown in pitch angle. The relative height accuracy reach 1.497m which can meet the accuracy requirement, if the satellite attitude measurement and determination accuracy reach 0.4″ and the stability accuracy of the angle between the star tracker and the camera reach 0.1″. The method using geometric chain to analyze the geolocation accuracy is applicable to the geolocation accuracy index assignment of high resolution optical remote sensing satellite.

geometric chain; height accuracy; index assignment; optical remote sensing; high resolution satellite

（编辑：夏淑密）

P228.1

A

1009-8518(2016)03-0111-09

10.3969/j.issn.1009-8518.2016.03.013

夏中秋，男，1985年生，现在中国空间技术研究院飞行器设计专业攻读博士学位。研究方向为空间光学遥感器总体设计。E-mail：xiazhongqiu@hotmail.com。

2016-03-16