群环Zn[i]G的零因子图的性质
唐高华,李 玉,吴严生
(广西师范学院数学与统计科学学院,广西南宁530001)
群环Zn[i]G的零因子图的性质
唐高华,李 玉,吴严生
(广西师范学院数学与统计科学学院,广西南宁530001)
本文主要研究由模n高斯整数环Zn[i]和素数阶循环群G构成的群环Zn[i]G的零因子图的性质,分别给出了Zn[i]G的零因子图的围长、平面性和直径的完全刻画。
群环;零因子图;围长;平面性;直径
0 引言
1988年,Beck在文献[1]中最早给出交换环的零因子图Γ(R)的定义:R中的每个元素都是Γ(R)的顶点,2个不同的顶点y与x有一条边相连当且仅当xy=0。1999年Anderson和Livingston在文献[2]中对Beck关于交换环的零因子图的定义进行了修改,以环R的非零零因子集D(R)*为图Γ(R)的顶点集,2个不同的顶点y与x有一条边相连当且仅当xy=0,并得出了关于环R的零因子图的一些基本结果:对任意的交换环R,R的零因子图Γ(R)是连通的,Γ(R)的直径只能为0、1、2、3,Γ(R)的围长只能为3、4、∞。唐高华、苏华东等在文献[3-6]给出了模n高斯整数环Zn[i]的单位群、素谱、零因子等代数结构及其零因子图的直径、平面性、围长、类数、中心集、半径等图结构的刻画。2015年,郭述峰等在文献[7]中刻画了群环ZnG的零因子图的围长、直径和平面性,其中G为素数阶群。本文主要完全刻画群环Zn[i]G的零因子图Γ(Zn[i]G)的围长、平面性和直径,其中Zn[i]={a+bi|a,b∈Zn,i2=-1}为模n高斯整数环,G=〈a:ap=1〉为素数p阶群。
图Γ是完全图是指它的每一对不同的顶点都有一条边相连。用Kn表示含有n个顶点的完全图,用Kn,m表示完全二部图。图Γ上的两点u、v之间的距离是指u和v之间的所有路径中最短的长度,记为d(u,v)。图Γ的直径diam(Γ)=sup{d(u,v)|u,v∈V(Γ)}。图Γ的围长是指图Γ中最短的圈长,用gr(Γ)表示,若图Γ中不含圈,则定义gr(Γ)=∞。图Γ是平面图是指它能画在平面上使得它的边仅在端点相交。用|A|表示集合A的基数,A*=A-{0},J(R)表示环R的Jacobson根。
1 预备知识
引理1(文献[8]定理9.10) 一个图是平面图当且仅当它不包含K5或K3,3的剖分图。
引理2(文献[9]命题19.10) 设K是一个特征为p>0的域,G是一个有限p群,则KG为局部环,且KG的增广理想就是它的Jacobson根,J(A)|G|=0,A/radA≌K。
引理3(文献[9]命题19.11) 设(R,m)是一个交换局部环且K=R/m的特征p>0,则对任意的有限p群G,群代数A=RG是一个局部环。

由引理4可推出引理5。
引理5 设n与p为互不相同的素数,则:

②当p|(n-1)时,xp-1+…+x+1在Zn[x]中完全可约。
引理6 设Zn[i]为模n高斯整数环,n≡3(mod 4),且n和p为互不相同的素数,则同余方程xp≡1(modn)有除1以外的解当且仅当p|(n2-1)。
证明 当n≡3(mod 4),且n为素数时,Zn[i]为n2元有限域,其单位群是n2-1阶的循环群,则xp≡1(modn)在Zn[i]中有除1以外的解当且仅当p|(n2-1)。证毕。
综合引理5与引理6易知存在互不相同的素数n和p,使得xp-1+…+x+1在Zn[x]中不可约但在Zn[i][x]中可约。
引理7(文献[7]定理1) 设Zn为模n剩余类环,G为素数p阶群,则:
①gr(Γ(ZnG))=∞当且仅当以下条件之一成立:
(a)n=p=2;
(b)n=2,p≠2。
②gr(Γ(ZnG))=3当且仅当以下条件之一成立:
(a)p|n且当p=2时n≠2;
(b)(p,n)=1且n为合数;
(c)n与p为互不相同的素数,p≠2,且p|(n-1)。
③gr(Γ(ZnG))=4当且仅当以下条件之一成立:
(a)p=2,n为奇素数;

引理8(文献[5]定理3) 设R=Zn[i],则:
①当n=2,p或2p,p是素数且p≡3(mod 4)时,gr(Γ(R))=∞;
②当n=p1p2,且p1、p2均是模4 余3的素数或n=p,p是模4余1的素数时,gr(Γ(R))=4;
③其他情况下,gr(Γ(R))=3。
引理9(文献[11]推论3.6.9) 设R是一个环,G是一个有限群,如果|G|在R中可逆,则RG≌R⊕Δ(G)。
引理10(文献[12]定理22)Γ(Zn[i])是平面图当且仅当n=2或4。
引理11(文献[7]定理3) 设Zn为模n剩余类环,G为素数p阶群,则Γ(ZnG)为平面图当且仅当以下情形之一成立:
①n=p=2;②n=p=3;③n=4,p=2;④n=3,p=2;⑤n=2,p≠2;⑥n=3,p≥5。
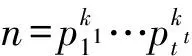
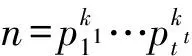
引理13 设Zn[i]为模n高斯整数环,G=〈a〉为素数p阶群,(n,p)=1,Δ(G)为群环Zn[i]G的增广理想,则a-1是Δ(G)中的正则元,即若(a-1)β=0,β∈Δ(G),则必有β=0。
证明 若(a-1)β=0,β∈Δ(G),则存在xi∈Zn[i],i=1,2,…,p-1,使得β=x1(a-1)+x2(a2-1)+…+xp-1(ap-1-1)。 于是(a-1)β=(x1+x2+…+2xp-1)-(2x1+x2+…+xp-1)a+(x1-x2)a2+…+(xp-2-xp-1)ap-1=0,从而xi=x1,∀2≤i≤p-1,故有px1=0,又(p,n)=1,所以x1=0,于是β=0,故a-1是Δ(G)中的正则元。证毕。

图1 Z2[i]G的零因子图Fig.1 The zero-divisor graphof Z2[i]G
引理14(文献[2]定理2.3) 设R是交换环,则Γ(R)是连通图,且diam(Γ(R))≤3。
下面先给出1个有用的例子。
例1 设Z2[i]为模2高斯整数环,G=〈a〉为2阶群,则Z2[i]={0,1,i,1+i},G={1,a},D(Z2[i]G)={0,1+i,(1+i)a,1+a,i(1+a),1+i+(1+i)a,i+a,1+ia},Z2[i]G的零因子图如图1所示,易知Γ(Z2[i]G)的直径为2,围长为3,它是平面图。
2 Γ(Zn[i]G)的围长
由于群环ZnG的零因子图是群环Zn[i]G的零因子图的子图,结合图的围长的定义及引理7,我们可得到下面引理15。
引理15 设Zn[i]为模n高斯整数环,G为素数p阶群,若以下条件(a)、(b)、(c)中有一个成立,则gr(Γ(Zn[i]G))=3:
(a)p|n且当p=2时n≠2;
(b)(p,n)=1且n为合数;
(c)n与p为互不相同的素数,p≠2,且p|(n-1)。
因此,要刻画群环Zn[i]G的零因子图的围长,只需要考虑以下4种情况:
①n=p=2;
②n=2,p≠2;
③p=2,n为奇素数;

下面以引理的形式分别就上面4种情况给出结果。
引理16 设Zn[i]为模n高斯整数环,G为素数p阶群,则:
①n=p=2时,gr(Γ(Zn[i]G))=3;
②n=2,p≠2时,gr(Γ(Zn[i]G))=3。
证明 当n=p=2时,由例1知,gr(Γ(ZnG))=3。当n=2,p≠2时,在Γ(Zn[i]G)中,1+i—(1+i)a—(1+i)a2—1+i构成一个长为3的圈,故gr(Γ(Zn[i]G))=3。证毕。
引理17 设Zn[i]为模n高斯整数环,G为素数p阶群,则:
①p=2,n为奇素数且n≡3(mod 4)时,gr(Γ(Zn[i]G))=4;
②p=2,n为奇素数且n≡1(mod 4)时,gr(Γ(Zn[i]G))=3。
证明 当p=2,n为奇素数且n≡3(mod 4)时,Zn[i]为n2元有限域,且易知Zn[i]G≌Zn[i]⊕Zn[i],此时Zn[i]G是2个域的直和,故Γ(Zn[i]G)是完全二部图。又因为|Zn[i]|≥9,故gr(Γ(Zn[i]G))=4。当p=2,n为奇素数且n≡1(mod 4)时,由引理8知gr(Γ(Zn[i]))=4,不妨设x—y—w—z—x是Γ(Zn[i])中的一个圈。再由引理9知,Zn[i]G≌Zn[i]⊕Δ(G),于是(x,0)—(y,z(a-1))—(0,x(a-1))—(x,0) 就是Γ(Zn[i]G)中的一个圈,故gr(Γ(Zn[i]G))=3。证毕。


②当n≡3(mod 4),p|(n+1)时,gr(Γ(Zn[i]G))=3;
③当n≡1(mod 4)时,gr(Γ(Zn[i]G))=3。

(1,0,0,…,0)—(0,1,0,…,0)—(0,0,1,0,…,0)—(1,0,0,…,0)
构成一个长为3的圈,故gr(Γ(Zn[i]G))=3。 当n≡1(mod 4)时,类似引理17可证,gr(Γ(Zn[i]G))=3。证毕。
综合引理15~18,我们给出群环Zn[i]G的零因子图的围长的一个刻画:
定理1 设Zn[i]为模n高斯整数环,G为素数p阶群,则:
①gr(Γ(Zn[i]G))=3当且仅当以下条件之一成立:
(a)p|n且当p=2时n≠2;
(b)(p,n)=1且n为合数;
(c)n与p为互不相同的素数,p≠2,且p|(n-1);
(d)n=p=2;
(e)n=2,p≠2;
(f)p=2,n为奇素数且n≡1(mod 4);


②gr(Γ(Zn[i]G))=4当且仅当以下条件之一成立:
(a)p=2,n为奇素数且n≡3(mod 4);

3 Γ(Zn[i]G)的平面性
设Zn[i]为模n高斯整数环,G为素数p阶群。由于Γ(Zn[i])与Γ(ZnG) 都是Γ(Zn[i]G)的子图,由引理10及引理11知,要刻画Zn[i]G的零因子图的平面性,只需要考虑以下3种情况:
①n=p=2;
②n=4,p=2;
③n=2,p≠2。
定理2 设Zn[i]为模n高斯整数环,G为素数p阶群,则Γ(Zn[i]G) 是平面图当且仅当n=p=2。
证明 ①当n=p=2时,由例1知,Γ(Zn[i]G)是平面图。
②当n=4,p=2时,集合I={2,2i,2ia,2+2i,2+2a}⊆D(Zn[i]G)*,且集合I中的点构成一个完全图K5,由引理1知,此时Γ(Zn[i]G)是非平面图。
③当n=2,p≠2时,由引理9知,Z2[i]G≌Z2[i]⊕Δ(G),此时|Z2[i]|=4,|Δ(G)|≥ 4p-1>4。由于Z2[i]×{0}中的点与{0}×Δ(G)中的点相连,所以K3,3是Γ(Zn[i]G)的子图。由引理1知,Γ(Zn[i]G)是非平面图。证毕。
4 Γ(Zn[i]G)的直径
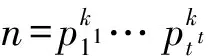
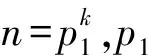
证明 当p1≠p时,p在Zn[i]中可逆,由引理9得,Zn[i]G≌Zn[i]⊕Δ(G)。因为n为合数,Zn[i]中有非零零因子x,于是,(x,a-1),(1,0)均为Zn[i]⊕Δ(G)的非零零因子。由于(x,a-1)(1,0)=(x,0)≠(0,0),故d((x,a-1),(1,0))≥2。由引理13得,a-1为Δ(G)中的正则元,于是Ann((x,a-1))={(y,0)|y∈Zn[i],xy=0}。又因为Ann((1,0))={(0,x)|x∈Δ(G)},所以Ann((x,a-1))∩Ann((1,0))={(0,0)},于是d((x,a-1),(1,0))≥3,由引理14知,diam(Γ(Zn[i]G))=diam(Γ(Zn[i]⊕Δ(G)))=3。证毕。
引理20 设Zn[i]为模n高斯整数环,n为素数,G为素数p阶群,n≠p,则:
①n=2时,diam(Γ(Zn[i]G))=3;
②n≡1(mod 4)时,diam(Γ(Zn[i]G))=3;
③n≡3(mod 4),p|(n-1)且p=2时,diam(Γ(Zn[i]G))=2;
④n≡3(mod 4),p|(n-1)且p≠2时,diam(Γ(Zn[i]G))=3;


证明 ①当n=2,n≠p时,由引理9知,Z2[i]G≌Z2[i]⊕Δ(G)。因为1+i为Z2[i]中的非零零因子,类似引理19知,d((1+i,a-1),(1,0))=3,故diam(Γ(Z2[i]G))=diam(Γ(Z2[i]⊕Δ(G)))=3。
②当n≡1(mod 4)时,由引理9知,Zn[i]G≌Zn[i]⊕Δ(G)。由于Zn[i]中有非零的零因子,类似引理19可证diam(Γ(Zn[i]G))=diam(Zn[i]⊕Δ(G))=3。
③当n≡3(mod 4)时,Zn[i]为有限域,若p|(n-1),则由引理5知,Zn[i]G≌Zn[i]⊕…⊕Zn[i](共p个Zn[i])。当p=2时,Zn[i]G≌Zn[i]⊕Zn[i],此时,Γ(Zn[i]G)为完全二部图,故diam(Γ(Zn[i]G))=2。当p≠2时,易知d((0,1,…,1),(1,0,1,…,1))=3,故diam(Γ(Zn[i]G))=3。

引理21 设Zn[i]为模n高斯整数环,G为素数p阶群,n=p,则:
①p=2时,diam(Γ(Zn[i]G))=2;
②p≡3(mod 4)时,diam(Γ(Zn[i]G))=2;
③p≡1(mod 4)时,diam(Γ(Zn[i]G))=3。
证明 当n=p=2时,由例1知,diam(Γ(Zn[i]G))=2。
当p≡3(mod 4)时,Zn[i]为特征大于0的n2元有限域,G为有限p群,由引理2知,Zn[i]G是局部环,其唯一的极大理想m=Δ(G)=〈a-1〉,于是D(Zn[i]G)=〈a-1〉。由于(2a-2)(a-1)=2a2-4a+2≠ 0,故d((2a-2),(a-1))≥2。对任意的x,y∈D(Zn[i]G)*,x≠y,则存在μ,υ∈Zn[i]G,使得x=μ(a-1),y=υ(a-1)。因为x(ap-1+ap-2+…+x+1)=μ(a-1)(ap-1+ap-2+…+x+1)=0,y(ap-1+ap-2+…+x+1)=υ(a-1)(ap-1+ap-2+…+x+1)=0,所以d(x,y)≤2,故diam(Γ(Zn[i]G))=2。
当p≡1(mod 4)时,Zn[i]≌Zn⊕Zn,于是Zn[i]G≌ZnG⊕ZnG,类似引理12可证,此时,diam(Γ(Zn[i]G))=3。证毕。
引理22 设Zn[i]为模n高斯整数环,G为素数p阶群,n=pk,k>1,则:
①p=2时,diam(Γ(Zn[i]G))=2;
②p≡3(mod 4)时,diam(Γ(Zn[i]G))=2;
③p≡1(mod 4)时,diam(Γ(Zn[i]G))=3。
证明 当p=2时,Zn[i]为局部环,其唯一的极大理想I=〈1+i〉且Zn[i]/I≌Z2。由引理3知,Zn[i]G为局部环,其唯一的极大理想m=IG+〈a-1〉。2a、a-1为Zn[i]G的不同的非零零因子,2a(a-1)=2-2a≠0,于是d(2a,a-1)≥2。对任意的x,y∈D(Zn[i]G)*,x≠y,存在α1,β1∈IG,α2,β2∈Zn[i]G, 使得x=α1+α2(a-1),y=β1+β2(a-1)。因为(-i)k(1+i)2k-1α1=(-i)k(1+i)2k-1β1=0,所以(-i)k(1+i)2k-1(ap-1+ap-2+…+x+1)x=0,(-i)k(1+i)2k-1(ap-1+ap-2+…+x+1)y=0。故d(x,y)≤2,因此,diam(Γ(Zn[i]G))=2。
当p≡3(mod 4)时,Zn[i]为局部环,其唯一的极大理想I=〈p〉且Zn[i]/I≌Zp[i]。由引理3知,Zn[i]G为局部环,其唯一的极大理想m=IG+〈a-1〉。pa、a-1为Zn[i]G的不同的非零零因子,pa(a-1)=pa2-pa≠0,于是d(pa,a-1)≥2。对任意的x,y∈D(Zn[i]G)*,x≠y,存在α1,β1∈IG,α2,β2∈Zn[i]G,使得x=α1+α2(a-1),y=β1+β2(a-1)。因为pk-1α1=pk-1β1=0,所以pk-1(ap-1+ap-2+…+x+1)x=0,pk-1(ap-1+ap-2+…+x+1)y=0。故d(x,y)≤2,因此,diam(Γ(Zn[i]G))=2。
当p≡1(mod 4)时,由文献[5]定理1知,p有不可约分解p=(c+bi)(c-di),Zn[i]只有2个极大理想m1=〈c+bi〉,m2=〈c-bi〉且d((c+bi),(c-di))=3。下面将证:在群环Zn[i]G的零因子图中d((c+bi),(c-di))=3。因为k>1,(c+bi)(c-di)=p≠0,所以d((c+bi),(c-di))≥2。易知,Ann(c+bi)={(c-bi)pk-1x|x∈Zn[i]G,c+bi不能整除x},Ann(c-bi)={(c+bi)pk-1y|y∈Zn[i]G,c-bi不能整除y}且Ann(c+bi)∩Ann(c-bi)=0,于是d((c+bi),(c-di))≥3,由引理14知,diam(Γ(Zn[i]G))=3。证毕。
综合引理12及引理19~22,我们给出群环Zn[i]G的零因子图的直径的完全刻画:
定理3 设Zn[i]为模n高斯整数环,G为素数p阶群,则:
①diam(Γ(Zn[i]G))=2当且仅当以下条件之一成立:
(a)n≡3(mod 4),n为奇素数,且p=2;

(c)n=pk(k≥1),且p=2或p≡3(mod 4)。
②其他情况下,diam(Γ(Zn[i]G))=3。
[1] BECK I. Coloring of commutative rings[J]. Journal of Algebra,1988,116(1):208-226. DOI:10.1016/0021-8693(88)90202-5.
[2] ANDERSON D F,LIVINGSTON P S. The zero-divisor graph of a commutative ring[J]. Journal of Algebra,1999,217(2):434-447. DOI:10.1006/jabr.1998.7840.
[3] 唐高华,苏华东,易忠.Zn[i]的单位群结构[J]. 广西师范大学学报(自然科学版),2010,28(2):38-41. DOI:10.16088/j.issn.1001-6600.2010.02.004.
[4] 苏华东,唐高华.Zn[i]的素谱和零因子[J]. 广西师范学院学报(自然科学版),2006,23(4):1-4. DOI:10.16601/j.cnki.issn1001-8743.2006.04.001.
[5] 唐高华,苏华东,赵寿祥.Zn[i]的零因子图的性质[J]. 广西师范大学学报(自然科学版),2007,25(3):32-35.DOI:10.16088/j.issn.1001-6600.2007.03.002.
[6] SU Huangdong. Central sets and radii of the zero-divisor graph of Gaussian integers modulon[J]. Guangxi Sciences,2012,19(3):221-223. DOI:10.13656/j.cnki.gxkx.2012.03.019.
[7] 郭述锋,谢光明,易忠. 群环ZnG的零因子图的性质[J]. 广西师范大学学报(自然科学版),2015,33(2):68-75. DOI:10.16088/j.issn.1001-6600.2015.02.011.
[8] BONDY J A, MURT U S R. 图论及其应用[M]. 吴望名,译. 北京:科学出版社,1984:163.
[9] LAM T Y. A first course in noncommutative rings[M]. New York: Spring-Verlag,1991:299.
[10] 潘承洞,潘承彪. 初等数论[M]. 北京:北京大学出版社,1992:231.
[11] MILIES C P,SEHGAL S K. An introduction to group rings[M]. Dordrecht:Kluwer Academic Publishers,2002:154.
[12] OSBA E A,AL-ADDASI S,JARADEH N A. Zero divisor graph for the ring of Gaussian integers modulon[J]. Communications in Algebra,2008,36(10):3865-3877.
(责任编辑 黄 勇)
Properties of Zero-divisor Graph of Group RingZn[i]G
TANG Gaohua,LI Yu, WU Yansheng
(School of Mathematics and Statistics,Guangxi Teachers Education University,Nanning Guangxi 530001,China)
LetGbe a cyclic group with prime order,Zn[i] be the Guassian integers modulonandZn[i]Gbe the group ring ofGoverZn[i]. Properties of the zero-divisor graph ofZn[i]Gare investigated in this paper and the girth,the planarity and the diameter of the zero-divisor graph ofZn[i]Gare completely characterized respectively.
group ring;zero-divisor graph;girth;planarity;diameter
10.16088/j.issn.1001-6600.2016.04.016
2016-03-10
国家自然科学基金资助项目(11661014,11661013,11461010);广西科学研究与技术开发资助项目(桂科合1599005-2-13,桂科攻1598010-3);广西自然基金重点资助项目(2016GXNSFDA380017);广西高校科学技术研究资助项目(KY2015ZD075)
唐高华(1965—),男,广西桂林人,广西师范学院教授,博士,博导。E-mail:tanggaohua@163.com
O153.3
A
1001-6600(2016)04-0109-07

