基于PCA特征距离的图像哈希算法

唐振军，杨 帆，黄紫晴，劳 欢

(1.广西师范大学广西多源信息挖掘与安全重点实验室，广西桂林541004；2.广西师范大学计算机科学与信息工程学院，广西桂林541004)

基于PCA特征距离的图像哈希算法

唐振军1，2，杨 帆1，2，黄紫晴1，2，劳 欢1，2

(1.广西师范大学广西多源信息挖掘与安全重点实验室，广西桂林541004；2.广西师范大学计算机科学与信息工程学院，广西桂林541004)

本文将主成分分析(PCA)应用于图像哈希，设计基于特征距离的感知哈希算法。该算法从规范化图像中构造适合于数据降维的二次图像，接着对其进行PCA处理，用PCA降维特征的距离生成哈希序列。实验结果表明本文算法的接收机操作特性曲线的分类性能优于现有的3种哈希算法。大规模图像库的拷贝检测显示，本文算法有较好的拷贝检测性能。

感知哈希函数；主成分分析；数据降维；图像拷贝检测；图像检索

0 引言

在大数据时代，人们获取和使用的图像日益增多，对图像的存储和管理提出许多挑战，亟待研究新的多媒体理论和技术以实现对图像大数据的高效处理。近年，多媒体领域的研究人员研究了感知哈希函数[1]。它可将任意图像映射成较短的数字序列，即图像哈希，有效降低了图像存储代价和相似计算的复杂度，目前已被成功应用于拷贝检测、图像检索、图像索引、图像取证等方面[2]。通常，图像哈希算法需要具备鲁棒性和唯一性[3-4]。鲁棒性是指对于视觉相似的2幅图像，不管其存储数据是否相同，哈希值应该相同或非常相似；而唯一性则要求不同内容的图像，其哈希值相同或相似的概率很低。当前，研究人员已设计出多种有效的图像哈希算法。根据这些算法的核心技术分类，可得到如下5大类算法。

①基于离散小波变换(DWT)的哈希算法。例如：Venkatesan等[3]利用DWT系数统计量、解码器和线性编码器生成哈希值；Mogna和Evans[5]提取线状目标的端点的小波系数构造哈希值；Ahmed等[6]用LL、LH和HL子带的小波系数构造中间哈希，再用SHA-1函数压缩。该类算法能较好抵抗JPEG压缩，但在旋转变换方面的稳健性较差。

②基于离散余弦变换(DCT)的哈希算法。例如：文献[1]利用DCT系数构造特征点并用点对间的距离构造哈希值；Lin和Chang[7]根据不同图像块的相同位置的DCT系数关系设计哈希算法；秦川等[8]提取DCT符号矩阵并用秘密共享机制生成哈希；Tang等[9]提出基于主导DCT系数的哈希算法，用第一行和第一列的若干DCT系数生成哈希。该类算法具有较好的唯一性，然而旋转稳健性仍然有待提高。

③基于积分变换的哈希算法。该类算法的常用技术是Radon变换(RT)和扇束(Fan-beam)变换。例如：Lefebvre等[10]最先提出利用RT构造图像哈希；Lei等[11]提取Radon变换域上的矩特征生成哈希值；Ou和Rhee[12]联合使用RT 和DCT提取哈希序列；Tang等[13]运用扇束变换提取图像哈希，该算法的分类性能和运算速度均优于常见的基于RT的哈希算法。由于积分变换具有较好的几何不变性，因此该类算法能较好抵抗旋转变换，但唯一性却不尽理想。

④基于离散傅里叶变换(DFT)的哈希算法。最早成功运用二维DFT技术设计哈希算法的研究人员为Swaminathan等[14]，他们提出在极坐标下表示DFT系数，对圆上的系数均匀采样并累加幅值，接着对累加结果伪随机加密得到中间哈希，最后通过量化压缩生成哈希。该算法能较好抵抗旋转变换，然而由于特征只依赖幅值而与相位无关，攻击者容易伪造哈希值。Wu等[15]联合使用RT、DWT和DFT，提出抗打印-扫描攻击的哈希算法，该算法具有较好的鲁棒性。Qin等[16]将DFT应用于二次图像，通过对幅值进行非均匀采样从而构造出哈希值。该类算法在旋转稳健性和唯一性方面的分类性能还不尽理想。

⑤基于矩阵分解的哈希算法。Kozat等[17]提出基于2次奇异值分解(SVD)的哈希方法，稳健性由SVD保证。受Kozat等启发，Monga等[18]提出用2次非负矩阵分解(NMF)的策略来计算哈希值。该算法对JPEG压缩、图像旋转等操作稳健，但对水印嵌入脆弱。Tang等[19]提出词典式图像哈希框架模型，并设计基于NMF和DCT的实现方案；在另外一项工作中，Tang等[20]发现正常处理前后的图像的NMF系数具有近似线性变化的性质，在此基础上提出了基于环形分割和NMF的哈希算法。最近，Ghouti[21]将四元数SVD应用于彩色图像哈希提取，该方法的分类性能优于传统的基于SVD的哈希算法，但仍有较大提升空间。

除上述算法外，研究人员也报道了一些其他哈希技术。Li等[22]运用Gabor滤波(GF)和格型矢量量化(LVQ)技术提取图像哈希；Tang等[23]设计基于颜色向量角和小波变换的图像哈希方法；Zhao等[24]综合利用Zernike矩和显著区域的统计特征来构造图像哈希。尽管研究人员已设计出多种有效的哈希算法，但实际应用中还存在诸多问题有待解决。例如，哈希算法在鲁棒性和唯一性方面的分类性能还不尽理想，在拷贝检测应用方面的性能仍有待提高。针对这些问题，本文将主成分分析(PCA)技术引入到图像哈希计算，设计基于PCA特征的高效算法。本文哈希算法不但具有较好的分类性能，而且还拥有优异的拷贝检测性能。

1 本文哈希算法

本文算法由预处理、二次图像构造、PCA特征压缩及量化3个阶段构成。预处理采用双三次插值法将图像尺寸调整为M×M，对于彩色图像，提取其亮度分量，公式如下：

I=0.114×B+0.587×G+0.298 9×R。

(1)

其中R是像素的红色分量，G是像素的绿色分量，B是像素的蓝色分量，I为像素的亮度分量。下面详细介绍二次图像构造、PCA特征压缩及量化和哈希相似测度。

1.1 二次图像构造

考虑到图像局部像素往往较相似，本文对图像进行非重叠分块，将图像块看作高维向量，确保向量元素有较好的相关性。接着把高维向量看作图像的列元素，随机排列向量即可生成二次图像。二次图像的具体构造步骤如下：

第一步，用d1×d2大小的图像块对图像亮度分量进行非重叠分块。为便于讨论，取M为d1和d2的整数倍，记S=d1×d2，于是图像块的像素总数为S。因此，输入图像共有N=M2/(d1×d2)=M2/S个块。本文的图像块按从左到右自上而下次序编号， 将第j个块记为Bj，其中1≤j≤N。

第二步，依次连接Bj的列元素，于是得到S×1大小的向量xj(1≤j≤N)，排列这些向量即可得到二次图像X：

X=[x1，x2，…，xN]。

(2)

图1 二次图像构造Fig.1 Construction of secondary image

图1是二次图像的构造示意图。与原图像相比，二次图像的列数(向量)较少，但每个列的元素较多(向量维度高)。用PCA对二次图像进行降维处理时，将有效降低向量维度，但并不改变向量个数，因此如果选定的降维维数不变，向量越少意味着降维后的数据越少，因此二次图像的构造实现初步的数据压缩。

1.2 PCA特征压缩及量化

PCA是一种高效的数据降维技术，已被广泛应用于数据挖掘、图像处理和模式识别等领域。考虑到二次图像的向量的维数较高，且向量内的元素存在较高的相关性，因此本文运用PCA去除相关性，以获取描述二次图像的相互独立的主要成分。用PCA处理二次图像的详细过程如下。

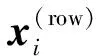
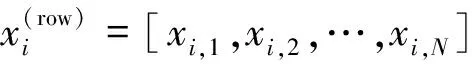
(3)

于是X可用公式(4)表示：

(4)

那么用PCA处理X，主要有3个步骤。

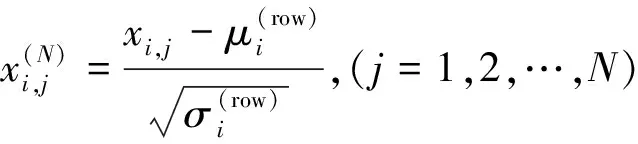
(5)

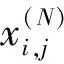
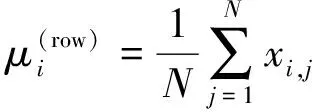
(6)

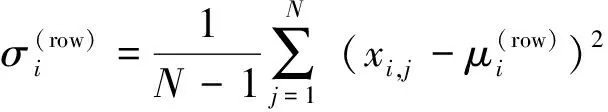
(7)

第二步，构造协方差矩阵。为了便于讨论，仍用X表示第一步计算得到的归一化矩阵，X的第i列向量(i= 1，2，…，N)用xi表示，于是协方差矩阵Cx的计算公式如下：

(8)

其中mx为xi的均值向量，定义如下：

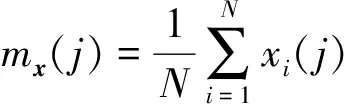
(9)

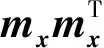
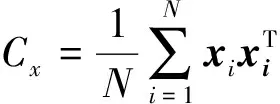
(10)

第三步，用雅可比方法求解Cx的特征值及相应特征向量。将Cx的特征向量及其特征值分别记为ai和λi(i=1，2，…，S)，并对特征值降序排列，即：λi≥λi+1，其中i=1，2，…，S-1。接着，用Cx的特征向量构造S×S大小变换矩阵A，其中λ1的特征向量为A的第一行元素，λ2的特征向量为A的第二行元素，依次类推，λS的特征向量为A的最后一行元素。于是，A乘上X即可得到Y：

YS×N=AS×SXS×N，

(11)

该表达式称为霍特林变换，也即PCA。实际中主要通过忽略特征值较小的特征向量实现降维。例如，令A(k)表示取A的前k行数据构造得到的矩阵，于是A(k)乘上X便可实现降维，具体公式如下：

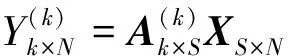
(12)

其中Y(k)为降维后的数据。如果需要从降维数据重构X，则可通过公式(13)近似重构：

X(k)=A(k)TY(k)。

(13)

此时重构结果X(k)与X的均方误差为：

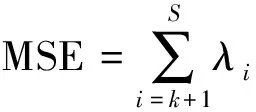
(14)

为了提取较短的哈希序列，对Y(k)进行压缩和量化。设Y(k)=[y1，y2，…，yN]，则具体计算过程如下。

第一步，计算参考向量y0=[y0(1)，y0(2)，…，y0(k)]T，其中y0(i)为y0的第i个元素，定义如下：

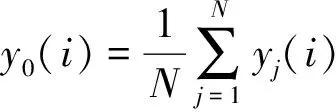
(15)

其中yj(i)为向量yj的第i个元素。

第二步，计算y0与yj的L2范数dj：

(16)

第三步，对dj进行取整操作，即：

hj=round(dj+0.5)，(j=1，2，…，N)，

(17)

其中round(·)表示取整计算。最后，哈希序列h可通过串连hj得到，即：

h=[h1，h2， …，hN]。

(18)

1.3 哈希相似测度

由于生成的哈希序列为N个十进制整数，因此本文算法用相关系数作为哈希序列的相似测度。设h1和h2为2幅图像的哈希序列，那么它们的相关系数计算公式如下：

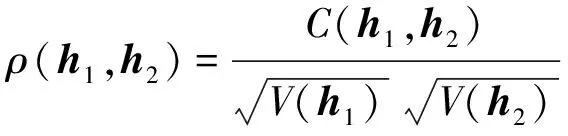
(19)

其中V(·)代表方差计算，C(·，·)代表协方差计算。如果ρ大于设定阈值，那么可判定h1和h2的对应图像是视觉相似的，否则它们是不同内容图像。

2 实验结果

实验的算法参数设置如下：M=512、d1=64、d2=64和k=5，因此哈希长度N=64。下面分别讨论鲁棒性、唯一性、哈希长度和参数影响。

2.1 鲁棒性

为了验证算法的鲁棒性，选取Airplane、Baboon、Girl、House、Lena、Peppers、Sailboat和Splash等8幅512×512的标准测试图像作为原始图像。用StirMark 4.0[25]、Photoshop和MATLAB等工具生成这些测试图像的相似图像，具体采用的数字操作包括：JPEG压缩、高斯低通滤波(3×3大小)、水印嵌入、亮度和对比度调整、伽玛校正、图像缩放和旋转变换等。各种操作的具体参数设置如下：JPEG压缩的质量因子为30，40，…，100；高斯低通滤波的均值为0、标准差为0.3，0.4，…，1.0；水印嵌入的强度为10，20，…，100；亮度和对比度调整的参数均为10和20；伽玛校正的γ值为0.75、0.9、1.1和1.25；缩放变换的比例为0.5、0.75、0.9、1.1、1.5和2.0；旋转变换的角度为5°、4°、3°、2°、1°、0.75°、0.5°和0.25°。经历这些操作后，每幅测试图像拥有60个相似版本，因此一共得到8×60=480幅相似图像。表1列出不同数字操作下的鲁棒性能，观察发现，所有操作的相关系数的平均值都大于0.940 0，说明本文算法可抵抗上述数字操作，鲁棒性较好。此外，除旋转变换外，其余操作的相关系数的最小值均大于0.940 0。因此，当阈值为0.940 0时，本文算法可正确识别出89.58%的相似图像。

2.2 唯一性

唯一性实验的测试图像库共有200幅彩色图像(用相机拍摄33幅，通过网站下载67幅，从华盛顿大学的公开图像库获取100幅)。图2为不同图像的哈希序列的相关系数分布，横坐标为相关系数，纵坐标为相关系数的出现频次。计算发现，最大的相关系数是0.852 9，最小的相关系数是-0.755 6，平均值和标准差分别为0.008 6和0.230 4。当阈值设为0.940 0时，没有一幅图像被误判为相似图像，说明本文算法的唯一性好。事实上，阈值越小，唯一性越差但鲁棒性越好；反之则唯一性提高而鲁棒性变差。表2列出不同阈值下的鲁棒性(相似图像的正确识别率)和唯一性(不同图像的误判率)。

表1 不同数字操作的鲁棒性能

图2 不同图像的哈希序列的相关系数的分布图Fig.2 Distribution of correlation coefficientsbetween hashes of different images

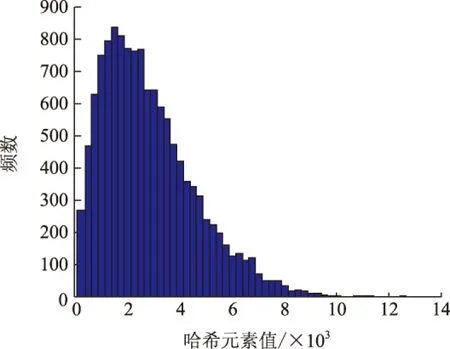
图3 12 800个哈希元素的分布图Fig.3 Distribution of 12 800 hash elements

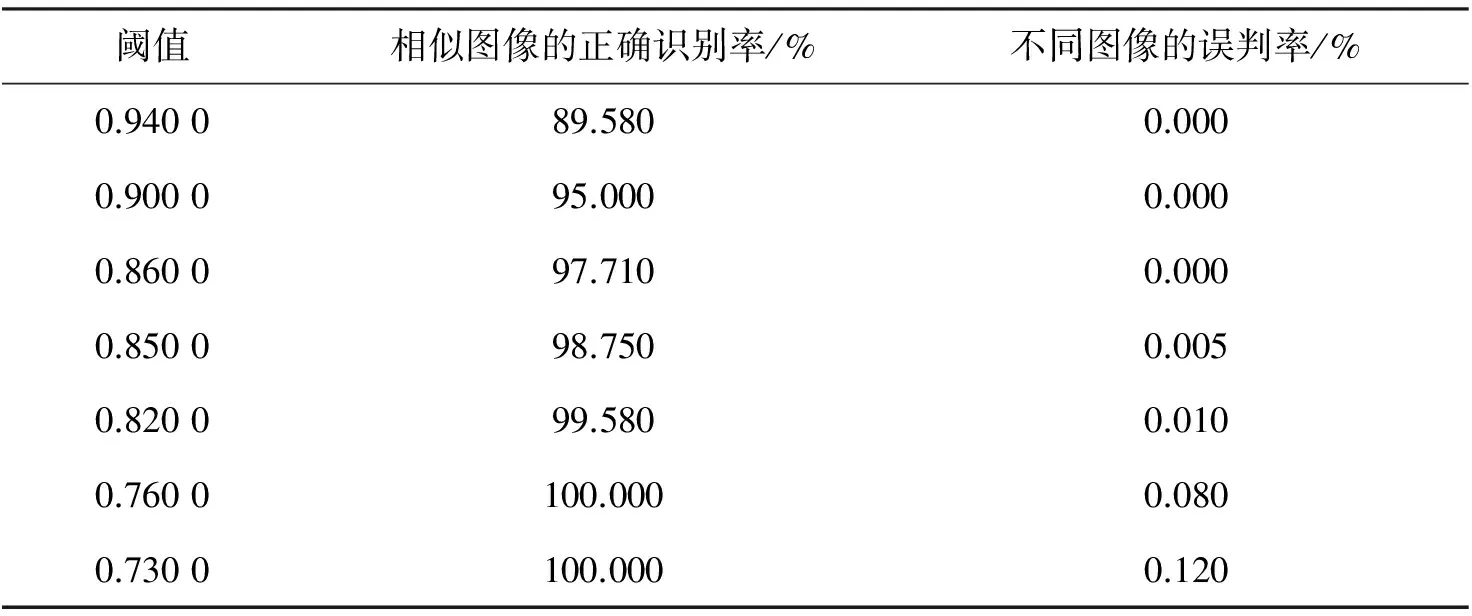
阈值相似图像的正确识别率/%不同图像的误判率/%0．940089．5800．0000．900095．0000．0000．860097．7100．0000．850098．7500．0050．820099．5800．0100．7600100．0000．0800．7300100．0000．120

2.3 哈希长度

为了分析本文哈希序列的长度，即实际存储所需的比特数，用唯一性实验的200个图像哈希作为统计的数据源，于是得到200×64=12 800个哈希元素。图3为这些元素的分布图，其中横坐标为哈希元素值，纵坐标为元素值的频数。计算发现，哈希元素的取值范围为0～12 487，而213=8 192<12 487<214=16 384，因此用14 bits即可表示一个哈希元素。因为本文的图像哈希共有64个元素，所以其长度为896 bits。

2.4 参数讨论

本节主要讨论分块模式和PCA降维维数对算法性能的影响，其中分块模式包括2种情况：不同分块个数和相同分块个数。实验过程中，我们仅改变讨论参数，测试图像仍沿用2.1节和2.2节的图像库。下面依次对这些情况进行讨论。

2.4.1 不同分块个数对哈希性能的影响

实验讨论的图像块大小分别为16×16、32×32和64×64，对应于1 024、256和64个图像块，即哈希的长度分别是1 024、256和64个整数。为了直观比较算法在不同参数设置下的分类性能，选取ROC(receiver operating characteristics)图[26]作为分析工具。在ROC图中，横坐标为错误接受率，主要反映唯一性，而纵坐标则为正确接受率，体现鲁棒性。图4是不同分块个数下的ROC曲线对比图。观察图4发现，图像块的个数较少时(如64和256)，ROC曲线靠近左上角。当图像块的个数增多(如1 024)，ROC曲线开始偏离左上角，整体分类性能下降。这是因为，与大的图像块相比，小的图像块更容易受局部数据变化的影响(数字操作引起)，导致鲁棒性下降。实验发现，选取64×64为图像块的大小时，本文算法有较好的整体分类性能。为了比较不同分块数的计算复杂度，分别记录各自唯一性实验的总时间(哈希提取)，由此计算出一个哈希的平均提取时间。实验用的CPU主频为3.20 GHz、内存为2.0 GB，算法实现平台是MATLAB 2012a。结果发现分块个数为64、256和1 024时(对应向量维度分别为4 096、1 024和256)，哈希的平均提取时间为7.741、0.505和0.224 s。因此，综合考虑各方面性能发现，选取64为图像块的个数时，本文算法有较好的整体性能。

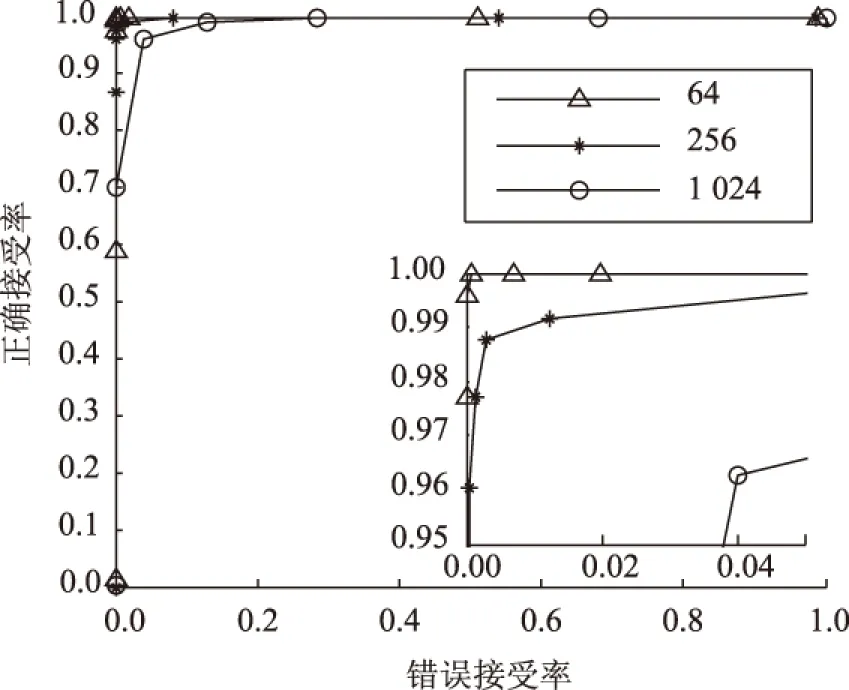
图4 不同分块个数的ROC曲线对比Fig.4 ROC curve comparisons underdifferent block numbers

图5 不同分块策略的ROC曲线对比Fig.5 ROC curve comparisons underdifferent strategies of block division

2.4.2 相同分块个数下的不同分块策略对性能的影响

实验中保持图像块的总数64不变，在此基础上，依次选择512×8、256×16、128×32和64×64等4种块尺寸对图像进行非重叠分块，分析不同分块策略对哈希性能的影响。图5为不同分块策略的ROC曲线对比。观察发现，64×64的图像块的ROC曲线位于其他曲线的上方。当图像块的宽高比差异大时，ROC曲线出现下降。这是因为像素在局部小范围内往往较为相似，由相似像素构造向量可确保二次图像的列元素具有较强的相关性，符合了PCA对输入数据的要求。当图像块的宽高比差异大时，列元素的相关性出现降低，因此从数据源上降低了PCA的去相关能力。此外，对不同块尺寸的哈希提取时间也进行了比较，结果发现512×8、256×16、128×32和64×64等4种块尺寸的运行时间分别为7.001、7.268、7.478和7.741 s，均在同一个数量级上，差异不明显。

2.4.3 PCA降维维数对性能的影响

实验选取的PCA降维维数包括k=1、k=2、k=5、k=10和k=20。图6为本文算法在不同k值下的ROC曲线图，观察发现这些降维维数均有较好的整体分类性能。此外，k=1时的分类性能要比其他k值的分类性能差；k=2已有较好的整体分类性能；k取5、10和20时的整体分类性能基本相同，并且均比k取1和2时的整体分类性能好。在计算复杂度方面，这些k值的平均哈希提取时间为7.370～8.100 s，差异较小。因此，综合考虑各方面指标，本文算法在k=5时的总体性能较好。

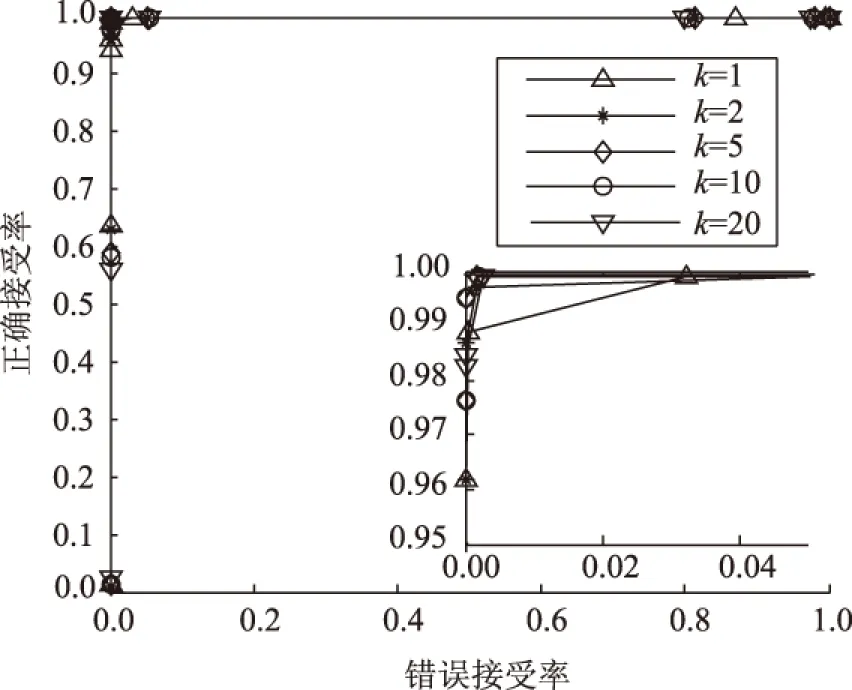
图6 不同维数的ROC曲线对比Fig.6 ROC curve comparisons under different dimensions

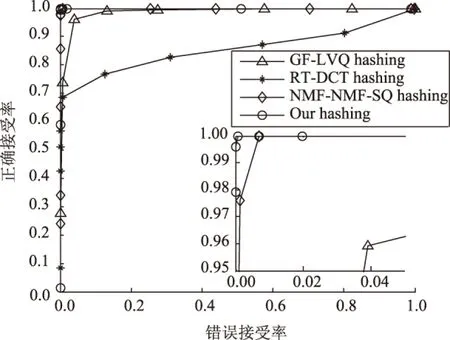
图7 不同哈希算法的ROC曲线比较Fig.7 ROC curve comparisons among various algorithms

3 算法性能比较

将本文算法与RT-DCT算法[12]、NMF-NMF-SQ算法[18]和GF-LVQ算法[22]作对比，测试图像仍采用2.1节和2.2节的图像库。图7是不同算法的ROC曲线对比结果，其中本文算法的ROC曲线是选取块总数为64、块大小为64×64和k=5时的结果。观察图7发现，NMF-NMF-SQ算法和本文算法的ROC曲线均靠近左上角，并且在另外2种哈希算法ROC曲线的上方。这说明NMF-NMF-SQ算法和本文算法的分类性能优于另外2种哈希算法。为了方便比较，将图7的左上角区域放大，于是得到其放大图(见图7的右下角区域)。对比发现，本文算法的曲线比NMF-NMF-SQ算法的曲线更靠近左上角。这说明在分类性能方面，本文算法优于NMF-NMF-SQ算法。在运行速度方面，RT-DCT算法、NMF-NMF-SQ算法和GF-LVQ算法的运行时间分别为0.455、1.298和0.285 s。本文算法的时间为7.741 s，速度慢于3种对比算法，这是因为PCA的计算复杂度较高。此外，RT-DCT算法的哈希长度是240 bits，GF-LVQ算法的长度是120 bits，NMF-NMF-SQ算法的长度是64个浮点数，而本文算法的长度是64个整数(即896 bits)。由此可见，本文算法的分类性能优于3种比较算法，哈希长度适中，不足之处是计算复杂度略高。

4 图像拷贝检测应用

为了测试拷贝检测性能，构造了一个较大的实验图像库。该图像库一共包含1 200幅图像，其中200幅图像是唯一性实验的图像集，1 000幅图像从Web网站下载得到。实验选取的查询图像为一幅中国画，如图8(a)所示。用不同数字操作对查询图像实施攻击以生成一系列拷贝版本，具体操作如下：伽玛值是0.75的伽玛校正；质量因子等于80的JPEG压缩；均值是0、标准差为0.8的3×3高斯低通滤波；α等于-4的3×3拉普拉斯滤波；强度是30的水印嵌入；比例是0.75的缩放变换；角度为5°的旋转变换；密度是0.02的椒盐噪声污染；添加印章；单元格尺寸等于10的马赛克滤波；均值是0、方差为0.02的乘性噪声污染。于是得到如图8(b)～(l)所示结果，将这些结果加入图像库，最终形成一个含1 211幅图像的测试集。

图8 一幅中国画及其11个拷贝版本Fig.8 A Chinese painting and its 11 copy versions

序号图像相关系数1图8(e)1．000002图8(i)0．999993图8(l)0．999974图8(d)0．999965图8(f)0．999956图8(c)0．999927图8(j)0．999608图8(h)0．999539图8(k)0．9993810图8(b)0．9976011图8(g)0．9199912其他图像0．5008713其他图像0．4612214其他图像0．4592215其他图像0．45276

表3列出与查询图像最相似的15幅图像(按相似系数取值降序排列)。由表3知，11个拷贝版本对应的相关系数的取值均大于0.900 00，而不同图像对应的相关系数的取值较小(最大值为0.500 87)。由此可见，拷贝版本与不同图像之间有较好的区分度。当选择0.900 00或0.850 00为阈值时，本文算法可准确识别拷贝版本与不同图像。此时，本文算法能够正确检测所有拷贝版本并且误判率为零，说明拷贝检测性能较好。

5 结论

本文设计了基于PCA特征的高效图像哈希算法。该哈希算法通过构造二次图像实现数据初步压缩，运用PCA达到数据降维，最终用特征距离生成较短的哈希序列。大量实验表明本文算法在鲁棒性和唯一性方面的分类性能较好，优于3种文献的哈希算法。拷贝检测结果显示，本文算法的识别率高，有较好的应用前景。下一步工作将研究快速PCA算法，在确保哈希性能不显著下降的前提下，有效提高运行速度。

[1] 唐振军,戴玉敏,张显全,等.基于DCT特征点的感知图像Hash函数 [J]. 广西师范大学学报(自然科学版), 2012, 30(3):135-141.DOI:10.16088/j.issn.1001-6600.2012.03.010.

[2] TANG Zhenjun,WANG Shuozhong,ZHANG Xinpeng,et al.Robust image hashing for tamper detection using non-negative matrix factorization [J]. Journal of Ubiquitous Convergence and Technology, 2008, 2(1):18-26.

[3] VENKATESAN R,KOON S M,JAKUBOWSKI M H,et al.Robust image hashing[C]//Proceedings of 2000 International Conference on Image Processing.Piscataway,NJ:IEEE Press,2000:664-666.DOI:10.1109/ICIP.2000. 899541.

[4] 刘凯,唐振军,张显全,等.联合压缩感知和颜色向量角的彩色图像哈希方法[J].应用科学学报,2015,33(6):595-603. DOI:10.3969/j.issn.0255-8297.2015.06.003.

[5] MONGA V,EVANS B L.Perceptual image hashing via feature points: performance evaluation and tradeoffs[J]. IEEE Transactions on Image Processing,2006,15(11):3453-3466. DOI:10.1109/TIP.2006.881948.

[6] AHMED F,SIYAL M Y,ABBAS V U.A secure and robust hash-based scheme for image authentication[J]. Signal Processing,2010,90(5):1456-1470. DOI:10.1016/j.sigpro.2009.05.024.

[7] LIN C Y,CHANG S F.A robust image authentication method distinguishing JPEG compression from malicious manipulation[J]. IEEE Transactions on Circuits and Systems for Video Technology,2001,11(2):153-168. DOI:10.1109/76.905982.

[8] 秦川,张真诚,郭成.基于秘密共享的感知鲁棒图像Hash算法[J].计算机研究与发展,2012,49(8):1690-1698.

[9] TANG Zhenjun,YANG Fan,HUANG Liyan,et al.Robust image hashing with dominant DCT coefficients[J]. Optik-International Journal for Light and Electron Optics,2014,125(18):5102-5107.DOI:10.1016/j.ijleo.2014.05.015.

[10] LEFEBVRE F,MACQ B,LEGAT J D.RASH:Radon soft hash algorithm[C]//Proceedings of 11th European Signal Processing Conference. Piscataway, NJ:IEEE Press, 2002:299-302.

[11] LEI Yanqiang, WANG Yuangen, HUANG Jiwu.Robust image hash in Radon transform domain for authentication [J].Signal Processing:Image Communication,2011,26(6):280-288. DOI:10.1016/j.image.2011.04.007.

[12] OU Yang,RHEE K H.A key-dependent secure image hashing scheme by using Radon transform[C]//Proceedings of the 2009 International Symposium on Intelligent Signal Processing and Communication Systems. Piscataway, NJ:IEEE Press,2009:595-598. DOI:10.1109/ISPACS.2009.5383770.

[13] TANG Zhenjun, HUANG Liyan, YANG Fan,et al.Robust image hashing based on fan-beam transform[J]. ICIC Express Letters,2014,8(8):2365-2372.

[14] SWAMINATHAN A,MAO Yinian,WU Min.Robust and secure image hashing[J].IEEE Transactions on Information Forensics and Security,2006,1(2):215-230. DOI:10.1109/TIFS.2006.873601.

[15] WU Di,ZHOU Xuebing,NIU Xiamu.A novel image hash algorithm resistant to print-scan[J].Signal Processing, 2009,89(12):2415-2424. DOI:10.1016/j.sigpro.2009.05.016.

[16] QIN Chuan,CHANG Chinchen,TSOU Peiling.Robust image hashing using non-uniform sampling in discrete Fourier domain[J].Digital Signal Processing,2013,23(2):578-585.DOI:10.1016/j.dsp.2012.11.002.

[17] KOZAT S S,VENKATESAN R, MIHCAK M K.Robust perceptual image hashing via matrix invariants[C]// Proceedings of 2004 International Conference on Image Processing.Piscataway,NJ:IEEE Press,2004:3443-3446. DOI:10.1109/ICIP.2004.1421855.

[18] MONGA V,MIHCAK M K.Robust and secure image hashing via non-negative matrix factorizations[J].IEEE Transactions on Information Forensics and Security,2007,2(3):376-390.DOI:10.1109/TIFS.2007.902670.

[19] TANG Zhenjun,WANG Shuozhong,ZHANG Xinpeng,et al.Lexicographical framework for image hashing with implementation based on DCT and NMF[J].Multimedia Tools and Applications,2011,52(2/3):325-345.DOI: 10.1007/s11042-009-0437-y.

[20] TANG Zhenjun,ZHANG Xianquan,ZHANG Shichao.Robust perceptual image hashing based on ring partition and NMF[J].IEEE Transactions on Knowledge and Data Engineering,2014,26(3):711-724. DOI:10.1109/TKDE. 2013.45.

[21] GHOUTI L.Robust perceptual color image hashing using quaternion singular value decomposition[C]// Proceedings of 2014 IEEE International Conference on Acoustic, Speech and Signal Processing. Piscataway,NJ: IEEE Press,2014:3794-3798.DOI:10.1109/ICASSP.2014.6854311.

[22] LI Yuenan, LU Zheming, ZHU Ce, et al.Robust image hashing based on random Gabor filtering and dithered lattice vector quantization[J].IEEE Transactions on Image Processing,2012,21(4):1963-1980.DOI:10.1109/TIP.2011.2171698.

[23] TANG Zhenjun,DAI Yumin,ZHANG Xianquan,et al.Robust image hashing via colour vector angles and discrete wavelet transform[J].IET Image Processing,2014,8(3):142-149. DOI:10.1049/iet-ipr.2013.0332.

[24] ZHAO Yan,WANG Shuozhong,ZHANG Xinpeng,et al.Robust hashing for image authentication using Zernike moments and local features[J].IEEE Transactions on Information Forensics and Security,2013,8(1):55-63.DOI: 10.1109/TIFS.2012.2223680.

[25] PETITCOLAS F A P.Watermarking schemes evaluation[J].IEEE Signal Processing Magazine,2000,17(5):58-64. DOI:10.1109/79.879339.

[26] FAWCETT T. An introduction to ROC analysis[J].Pattern Recognition Letters,2006,27(8):861-874.DOI:10.1016/ j.patrec.2005.10.010.

(责任编辑 黄 勇)

Image Hashing Algorithm Based on PCA Feature Distance

TANG Zhenjun1，2， YANG Fan1，2， HUANG Ziqing1，2， LAO Huan1，2

(1. Guangxi Key Lab of Multi-source Information Mining & Security， Guangxi Normal University， Guilin Guangxi 541004， China;2. College of Computer Science and Information Technology， Guangxi Normal University， Guilin Guangxi 541004， China)

Principal component analysis (PCA) is applied to image hashing algorithm and a perceptual hashing algorithm based on characteristic distance is proposed. In the proposed algorithm， a secondary image suitable for data dimension reduction is first constructed from the normalized image. Then， PCA is used to process secondary image， and the distance between PCA features is finally exploited to form image hash. Experimental results illustrate that classification performance of the proposed algorithm measured with receiver operating characteristics (ROC) curve is better than those of three existing hashing algorithms. Copy detection under a large-scale image database shows that the proposed algorithm has good performance in detecting image copies.

perceptual hash function； principal component analysis (PCA)； data dimension reduction； image copy detection； image retrieval

10.16088/j.issn.1001-6600.2016.04.002

2016-06-19

国家自然科学基金资助项目(61300109， 61363034， 61562007)；广西自然科学基金资助项目(2015GXNSFDA139040)；广西“八桂学者”工程专项经费资助项目；广西高等学校优秀中青年骨干教师培养工程资助项目(GXGQ012013059)；广西多源信息挖掘与安全重点实验室系统性研究基金资助项目(15-A-02-02， 14-A-02-02，13-A-03-01)

唐振军(1979—)，男，广西桂平人，广西师范大学教授，博士。E-mail：tangzj230@163.com

TP391

A

1001-6600(2016)04-0009-10