基于改进精英蚁群系统算法的四旋翼无人机姿态控制研究
钟海鑫,罗晓曙,赵 帅,杨 力,唐 堂
(广西师范大学电子工程学院,广西桂林541004)
基于改进精英蚁群系统算法的四旋翼无人机姿态控制研究
钟海鑫,罗晓曙,赵 帅,杨 力,唐 堂
(广西师范大学电子工程学院,广西桂林541004)
四旋翼无人机在飞行过程中姿态易受到外界气流等因素的干扰,导致飞行姿态失稳,影响完成预设飞行任务的质量。针对传统PID控制不能自适应调整其控制参数的特点,本文首先研究精英蚁群系统算法与PID控制结合的方法,然后提出一种改进精英蚁群系统算法与PID控制结合的方法,分别实现无人机在受到干扰情况下飞行过程的姿态控制,并进行了仿真实验对比。仿真实验结果表明:用改进精英蚁群系统算法优化PID控制参数,不仅可以在短时间内获得PID控制参数的最优解,提高了收敛速度,同时具有更好的抗扰性和鲁棒性。
PID控制;蚁群系统算法;抗扰性;鲁棒性
0 引言
四旋翼无人机(quadrotor unmanned aerial vehicle, QUAV)是一种可以通过遥控来实现自主飞行的非载人飞行器[1]。它是一种欠驱动系统,在4个无刷直流电机的驱动下产生差动力矩从而实现俯仰和翻滚运动,产生的反扭力矩实现偏航运动[2],飞行的轨迹可以由遥控器控制[3]。QUAV飞行运动具有多变量、强耦合、非线性等特点,且在飞行中易受到不确定干扰的影响,因此设计良好的姿态控制系统显得非常重要。
目前有许多控制方法来保持QUAV在飞行当中的稳定性,如:PID控制、滑模控制、模糊控制、反步法等[4-7],这些方法均对模型精确度有着很高的要求。其中,最为常见的控制方法是PID控制[8]。PID控制结构简单,鲁棒性较好[9]。在QUAV的实际飞行过程中,控制器的参数整定需要熟练的技巧和足够的时间,且调整好的参数不会自适应外界的变化,很难以一套固定的参数来完成控制目标的任务。在过去的几十年里出现了很多关于PID参数优化的方法,比如,ZN法、BP神经网络优化方法、模糊优化方法、蚁群算法(ant colony algorithm, ACA)优化方法等[10-13]。ZN法虽然简单实用,但其易引起较大的超调[14];BP神经网络结构简单,具有自学习的能力,但有可能在训练过程中出现不收敛的问题[15];模糊优化方法虽然可以增强控制系统的鲁棒性,但却使得控制精度降低[16];蚁群算法容易和其他的方法进行结合,可以提高系统的鲁棒性,实现参数优化,近些年来得到了国内外专家学者的关注[17-19],但蚁群算法易出现搜索时间长和搜索停滞的现象。精英蚁群系统(elitist ant colony system, EACS)是对Gambardella提出的蚁群系统(ant colony system, ACS)的一次改进[20],解决了此问题。
由文献[21]可知,EACS中参数ξ的选择会影响算法的性能,且EACS在某条路径上的信息素可能过大或者过小。针对这2个问题,本文提出一种改进的精英蚁群系统(improved elitist ant colony system, IEACS)算法,将其与PID控制算法结合来控制QUAV姿态,解决PID控制中参数不能自动调节的问题,使QUAV在飞行时更好地适应外界环境的变化,以提高无人机控制系统的抗扰性和鲁棒性。改进的精英蚁群系统算法可以在短时间内更好地获得最优解,相比EACS提高了收敛性。
1 EACS概述
蚁群算法[17]是一种在图中寻找优化路径的概率型方法,由意大利学者Marco Dorigo在其博士论文里提出。此方法最早解决了旅行商问题(travelling salesman problem, TSP)。
ACA是根据蚂蚁的寻路方式进行模拟,在行径过程中会释放一种信息素(pheromone),后来的蚂蚁可以通过信息素来调整自己的运动方向。因此,蚂蚁的行径方式表现出信息的正反馈,经过此路程的蚂蚁越多,后来的蚂蚁选择这条路的概率越大,最终找到最佳距离,如图1所示。只有在蚁群一起合作的时候才能寻找到这条最佳路径[21]。
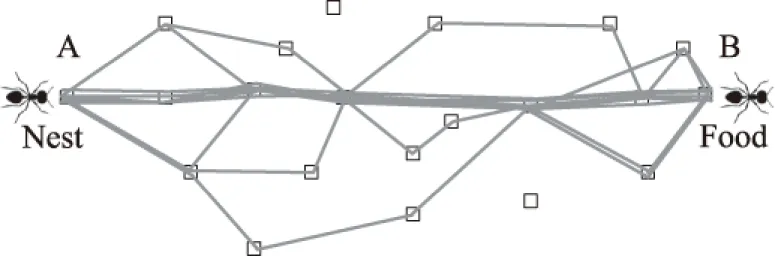
图1 蚂蚁寻找食物路径Fig.1 The path of ants’ looking for food
ACS是对ACA的改进,其采用了更优的选择规则、更优的信息素释放规则[22]。EACS是对ACS的改进,改变了全局信息素更新策略,解决了ACS收敛速度慢和优化解不易产生的问题[23]。
2 QUAV建模概述
QUAV的机体坐标系和惯性坐标系如图2所示,设定QUAV翻滚角、俯仰角和偏航角分别为φ、θ、ψ,l为其质心与旋翼中心之间的距离,Fv为其垂直升力,Ix、Iy、Iz为惯性主距[24],Ωi为第i个旋翼转速,IR为转动惯量,n1、n2分别为其升力系数和反扭矩系数。QUAV的动力学方程[25-26]为:
(1)
根据式(1),将其模型分解成4个独立的控制通道[27],考虑到在飞行当中,姿态角变动范围较小,可以把每个自由度看做独立的SISO线性系统[28],从而可得到每个通道的传递函数[29],具体参见文献[27-29]。

图2 QUAV的机体坐标系定义和惯性坐标系定义Fig.2 The definition of the body coordinate system and the inertial coordinate system of QUAV
3 EACS优化PID控制
基于EACS优化PID控制下QUAV系统结构图如图3所示。
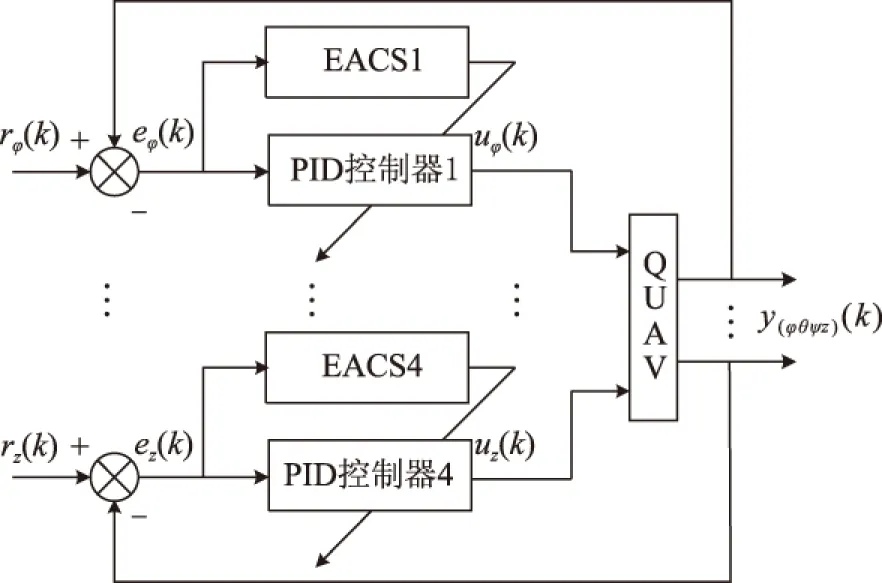
图3 基于EACS优化PID控制下的QUAV系统结构图Fig.3 Structure diagram of QUAV system based on EACS optimized PID control
PID控制采用增量式数字PID控制[30],其表达式为:

(2)
其中Kp为比例系数,e(k)为本次偏差,Δu(k)对应的控制量为u(k),T为采样周期,Ti为积分时间常数,Td为微分时间常数。PID控制需要确定的参数分别为Kp、Ti和Td。
在工程上评价控制系统的性能指标用式(3)表示[13]:
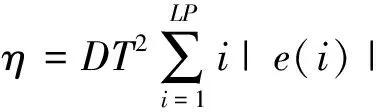
(3)
其中LP为仿真计算点数,DT为仿真计算步骤。
式(3)的连续形式为式(4):
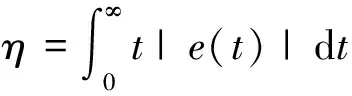
(4)
设蚂蚁总数为m,对于每一个蚂蚁,此时刻的点为i,其对应函数值为ηi,下一个可达的点j,对应函数值为ηj:
Δηij=ηi-ηj,∀i,j。
(5)
蚂蚁会朝着信息素最多的方向移动,当没有信息素时,便会按照原来的运动方向移动。蚂蚁在t时刻处于i点时朝着j点移动的概率为:

(6)
其中allowed为蚂蚁从地点i直接到达下一个路径点的集合,α为信息素的相对重要程度,β为距离信息的相对重要程度。α=0,最靠近i的地点j将有可能被选出,这类似于随机贪心算法[31]。β=0,蚂蚁只受到信息素的影响而忽略了启发式信息带来的偏向性。如果蚂蚁移动方向有障碍物时,则随机选择其他的方向;如果有信息素指引时,则按照其指引行动。寻优时蚂蚁的移动概率根据式(6)来确定:Δηij(t)<0表示蚂蚁在自身所在地点i的邻域搜索,感知并且行动;Δηij(t)>0表示蚂蚁按照移动概率从其自身所在地点i的邻域移动至j的邻域。
局部信息素更新策略为:
τij(t)=(1-ξ)τij(t-1)+ξτ0,
(7)
其中ξ∈(0,1),τ0为信息素初始值。
局部信息素更新策略的作用在于:蚂蚁经过路径(i,j),该路径的信息素τij将会减少,从而其他蚂蚁再选中此路径的概率减少。
全局信息素更新策略:
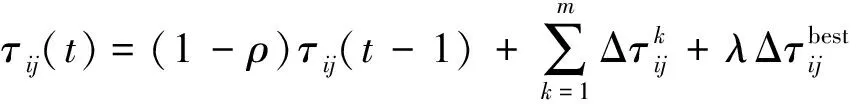
(8)
路径的构建:位于节点i的蚂蚁k在每次选择下一个路径前会产生一个随机数q,那么从节点i到节点j的移动规则为:
(9)
q是随机变量,均匀分布在区间[0,1]中,q0∈[0,1]。
4 IEACS优化PID控制
文献[21]表明ξ=0.1时,EACS算法有较好的性能。实验中也发现,当ξ在0.1附近取值时,EACS算法性能较好。因此,本文提出将局部信息素更新策略改进为:

(10)

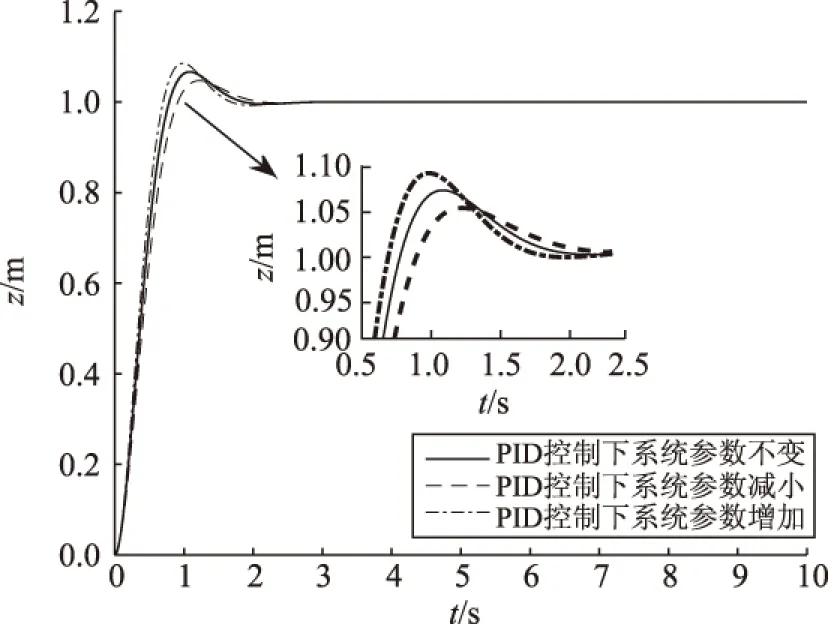
为防止EACS算法在某条路径上的信息素过大或者过小,本文提出加入信息素浓度区间:τ∈[τmin,τmax],由此来限定某些路径上的信息素增长过快来防止算法出现停滞现象,这样就把蚂蚁k从节点i到节点j的概率pij的取值区间定格在[pmin,pmax],其中有0 根据文献[31],可以设定信息素上界和下界的取值,a是一个参数[33]: (11) IEACS算法优化PID控制参数的方法同第3节,本节不再赘述。通过以上IEACS算法可以找到PID参数最优解。 由文献[13]可知,EACS和IEACS的进化代数和路径最优解决定了PID控制参数优化。 设蚂蚁数取10,循环取2 500代,选择概率取0.9,信息素因子取1,启发信息因子取2,EACS算法和IEACS算法的路径最优解曲线如图4所示,性能对比如表1。 图4 IEACS和EACS的路径最优解Fig.4 Path optimal solution of IEACS and EACS 图5 IEACS算法流程图Fig.5 Flow chart of IEACS algorithm 由图4和表1可知,IEACS最优解更好,进化代数更少。IEACS算法流程图如图5所示。 表1 IEACS和EACS算法性能对比 表2 控制性能指标对比 图6 偏航角姿态控制Fig.6 Yaw angle attitude control 以QUAV偏航角ψ为例,设初始值ψ0=0°,偏航角控制性能如图6和表2所示。以翻滚角φ为例,设初始值φ0=0°,飞行中受到的干扰用随机信号模拟,测试QUAV控制系统的抗扰性能,如图7所示。以高度z为例,设高度初始值为z0=0,再将质量m和惯性张量Ix、Iy、Iz分别减小30%和增加30%进行鲁棒性测试,如图8~10所示。 从图6可知,以偏航角为例,QUAV在IEACS算法优化下的PID控制性能略优于EACS算法优化下的PID控制,这2种算法优化下的PID控制均优于传统PID控制。从表2可知,IEACS-PID控制相比EACS-PID控制,超调量小1.30%,调整时间少0.81 s,上升时间少0.22 s。IEACS-PID控制相比传统PID控制,超调量小5.50%,调整时间少3.39 s,上升时间少0.67 s,全面提升了系统动态性能。从图7可知,IEACS-PID控制下的QUAV系统抗扰性能要略好于EACS-PID控制,好于传统PID控制。从图8~10可知,IEACS-PID控制下的QUAV对于参数不确定的鲁棒性略好于EACS-PID控制,好于传统PID控制。 图7 抗扰性能对比Fig.7 Anti-disturbance performance contrast 图8 PID控制下鲁棒性测试Fig.8 Robustness testing under PID control 图9 EACS-PID控制下鲁棒性测试Fig.9 Robustness testing under EACS-PID control 图10 IEACS-PID控制下鲁棒性测试Fig.10 Robustness testing under IEACS-PID control 综上,IEACS-PID控制下的QUAV姿态控制效果要优于EACS-PID控制,这2种控制均优于PID控制。 本文针对QUAV自身特性且其飞行姿态易受到不确定干扰的影响,提出了基于IEACS来优化PID控制参数。研究结果表明,IEACS相比EACS,收敛性得到了改善,弥补了传统PID控制不能实时自适应调整参数的缺陷,提高了QUAV飞行过程中的抗干扰能力和鲁棒性,改善了其动态性能,从而改善了QUAV的姿态控制性能,在无人机自动控制领域具有较好的实际应用价值。 [1] GUPTE S, MOHANDAS P I T, CONRAD J M. A survey of quadrotor unmanned aerial vehicles[C]//Southeastcon,2012 Processdings of IEEE.Piscataway NJ:IEEE Press,2012:1-6. [2] VOOS H. Nonlinear state-dependent riccati equation control of a quadrotor UAV[C]// 2006 IEEE Conference on Computer Aided Control System Design, 2006 IEEE International Conference on Control Applications, 2006 IEEE International Symposium on Intelligent Control. Piscataway NJ:IEEE Press, 2006:2547-2552. [3] ISSAM K, GENG Q. Research on control strategies for the stabilization of quadrotor UAV[C]// Intelligent Control and Information Processing.Piscataway NJ:IEEE Press, 2014:286-292. [4] JOYO M K, Hazry D, AHMED S F, et al. Altitude and horizontal motion control of quadrotor UAV in the presence of air turbulence[C]// Systems, Process & Control. Piscataway NJ:IEEE Press, 2013:74-77. [5] TANVEER M H, AHMED S F, HAZRY D, et al. Disturbance and noise rejection controller design for smooth takeoff/landing and altitude stabilization of quad-rotor[J]. Journal of Applied Sciences Research, 2013, 9(5):3316-3327. [6] BOUADI H, BOUCHOUCHA M, TADJINE M. Sliding mode control based on backstepping approach for an UAV type-quadrotor[J]. World Academy of Science, Engineering and Technology,2007,26(5):22-27. [7] RAZA S A, GUEAIEB W. Intelligent flight control of an autonomous quadrotor[M]//CASOLO F. Motion Control. Rijeka:InTech,2010:245-264. [8] ARGENTIM L M, REZENDE W C, SANTOS P E, et al. PID, LQR and LQR-PID on a quadcopter platform[C]// International Conference on Informatics, Electronics & Vision. Piscataway NJ:IEEE Press,2013:1-6. [9] ASTRÖM K J , MURRAY R M. Feedback systems: an introduction for scientists and engineers[M]. Princeton :Princeton University Press, 2008. [10] ZIEGLER J G,NICHOLS N B. Optimum settings for automatic controllers[J]. Journal of Dynamic Systems, Measurement, and Control,1993,115(2B):220-222. [11] JIN H S, JIN W L, LEE Y J, et al. Anti-sway control of an ATC using NN predictive PID control[C]// Industrial Electronics Society, 2004. Piscataway NJ:IEEE Press, 2004:2998-3003. [12] LI H X, ZHANG L, CAI K Y, et al. An improved robust fuzzy-PID controller with optimal fuzzy reasoning[J]. IEEE Transactions on Systems Man and Cybernetics, Part B (Cybernetics), 2005, 35(6):1283-1294. [13] 段海滨,王道波,黄向华,等. 基于蚁群算法的PID参数优化[J].武汉大学学报(工学版), 2004, 37(5):97-100. [14] ÅSTRÖM K J, HGGLUND T. Revisiting the Ziegler-Nichols step response method for PID control[J]. Journal of Process Control, 2004, 14(6):635-650. [15] RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representation by backpropagating errors[J]. Nature, 1986, 323(9):533-536. [16] WANG L X. Stable adaptive fuzzy control of nonlinear systems[J]. IEEE Transactions on Fuzzy Systems, 1992, 1(2):146-155. [17] COLORNI A, DORIGO M, MANIEZZO V. Distributed optimization by ant colonies[C]// Processdings of the Ecal 91 European Conference on Artificial Life. Paris: Elsevier Publishing, 1991:134-142. [18] HSIAO Y T, CHUANG C L, CHIEN C C, et al. Ant colony optimization for designing of PID controllers[C]// 2004 IEEE International Conference on Robotics and Automation. Piscataway NJ:IEEE Press,2004:321-326. [19] VERBEECK K, NOWE A. Colonies of learning automata[J]. IEEE Transactions on Systems Man and Cybernetics, Part B (Cybernetics), 2002, 32(6):772-780. [20] DORIGO M, STÜTZLE T. Ant Colony Optimization[M].北京:清华大学出版社,2007:71-72. [21] CARO G D, DORIGO M. Ant colonies for adaptive routing in packet-Switched communications networks[C]// International Conference on Parallel Problem Solving From Nature. Heidelberg:Springer-Verlag, 1998:673-682. [22] DORIGO M, GAMBARDELLA L M. Ant colony system: a cooperative learning approach to the traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1):53-66. [23] 谢剑斌,兴军亮,张立宁,等.视觉机器学习20讲[M]. 北京:清华大学出版社,2015:228-239. [24] 李滋刚,万德钧.捷联式惯性导航技术[M].北京: 中国船舶信息中心, 2001. [25] BOUABDALLAH S, SIEGWART R. Backstepping and sliding-mode techniques applied to an indoor micro quadrotor[C]// Proceedings of the 2005 IEEE International Conference on Robotics and Automation. Piscataway NJ:IEEE Press, 2005:2247-2252. [26] 王俊生,马宏绪,蔡文澜,等.基于ADRC的小型四旋翼无人直升机控制方法研究[J].弹箭与制导学报,2008,28(3):31-40. [27] CABECINHAS D, SILVESTRE C, CUNHA R, Vision-based quadrotor stabilization using a pan and tilt camera[C]//49th IEEE in Conference on Decision and Control. Piscataway NJ:IEEE Press, 2010: 1644-1649. [28] 王伟,马浩,孙长银.四旋翼飞行器姿态控制系统设计[J]. 科学技术与工程,2013, 13(19):5513-5519. [29] CARRILLO L G , RONDON E, SANCHEZ A, et al. Stabilization and trajectory tracking of a quad rotor using vision[J] Journal of Intelligent and Robotic Systems, 2011,61(1-4):103-118. [30] PRESS W, TEUKOLSKY S , VETTERLING, W. Numerical recipes 3rd edition: the art of scientific computing[M] Cambridge: Cambridge University Press, 2007. [31] DORIGO M, BIRATTARI M. Ant colony optimization[M]// Wiley Encyclopedia of Operations Research and Management Science. Hoboken:Emerald Group Publishing Limited,2011:1155-1173. [32] DORIGO M, MANIEZZO V, COLORNI A. Ant system: optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems, Man and Cybernetics, Part B (Cybernetics), 1996, 26(1):29-41. [33] STÜTZLE T, HOOS H. Improvements on the ant-system: introducing the MAX-MIN ant system[M]// Artificial Neural Nets and Genetic Algorithms. Vienna:Springer Vienna, 1998:245-249. (实习编辑 李 朝) (责任编辑 马殷华) Research on Attitude Stability Control of Quadrotor Unmanned AerialVehicle Based on Improved Elitist Ant Colony System Algorithm ZHONG Haixin, LUO Xiaoshu, ZHAO Shuai, YANG Li, TANG Tang (College of Electronic Engineering, Guangxi Normal University, Guilin Guangxi 541004, China) The altitude of Quadrotor Unmanned Aerial Vehicle (QUAV) is easy to be disturbed by the factors such as the external air flow during the flight, which leads to the instability of the flight attitude and impacts the quality of the preset flight mission. Aiming at the characteristics of the traditional PID control failing to adaptively adjust the control parameters, firstly, this paper studies the method of the combination between elitist ant colony system algorithm and PID control, and then proposes a method of improved elitist ant system algorithm to combine with PID control, respectively, to achieve QUAV’s altitude control during the flight under disturbance, finally the simulation experiment comparison is carried out. Simulation experimental results show that the improved elitist ant colony system algorithm that optimizes the parameters of PID control can not only get optimum valve in a short time and improve the speed of convergence, but also have a better performance of anti-disturbance and robustness. PID control; elitist ant colony system algorithm; anti-disturbance; robustness 10.16088/j.issn.1001-6600.2016.04.013 2016-07-19 国家自然科学基金资助项目(11262004);广西多源信息挖掘与安全重点实验室开放基金资助项目(MIMS15-06);广西信息科学实验中心基金资助项目(KA1430) 罗晓曙(1961—),男,湖北应城人,广西师范大学教授,博士。E-mail:lxs@mailbox.gxnu.edu.cn TP273.2; TP271 A 1001-6600(2016)04-0085-08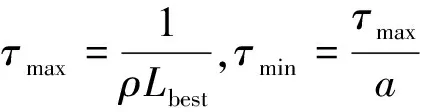
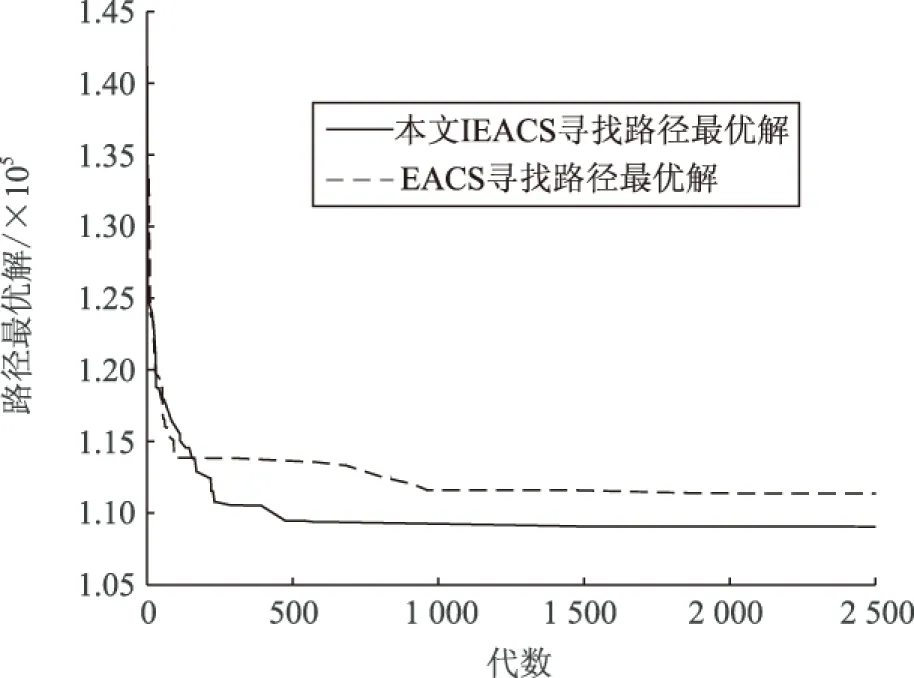
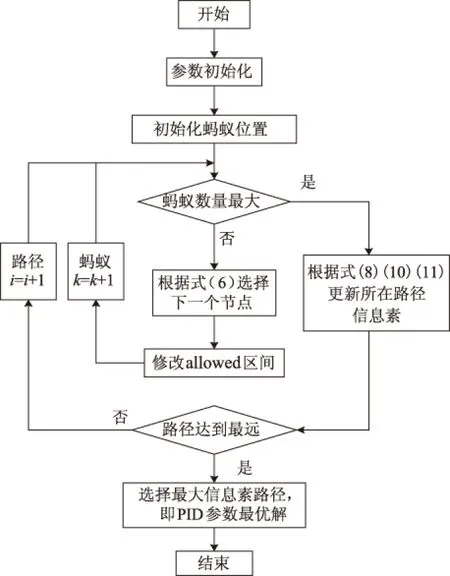
5 基于EACS和IEACS优化PID控制的QUAV对比仿真实验
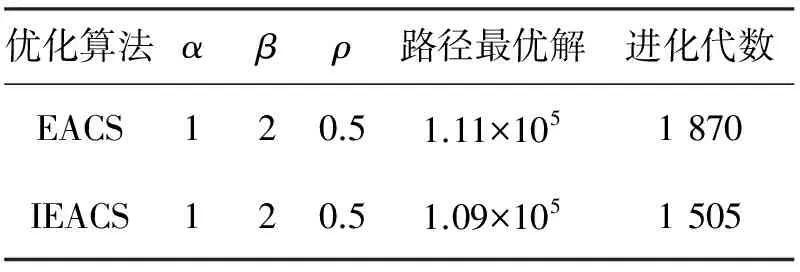
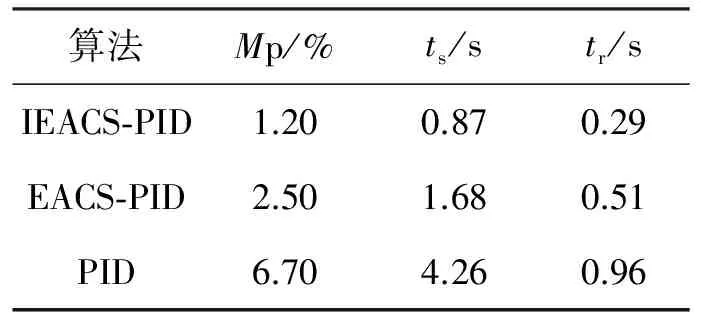
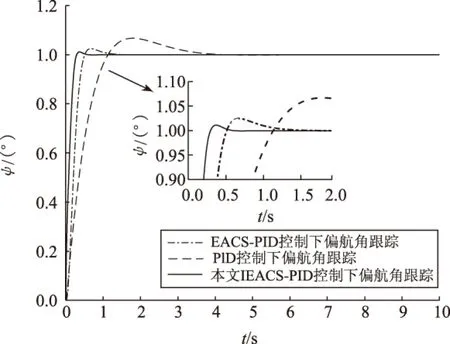
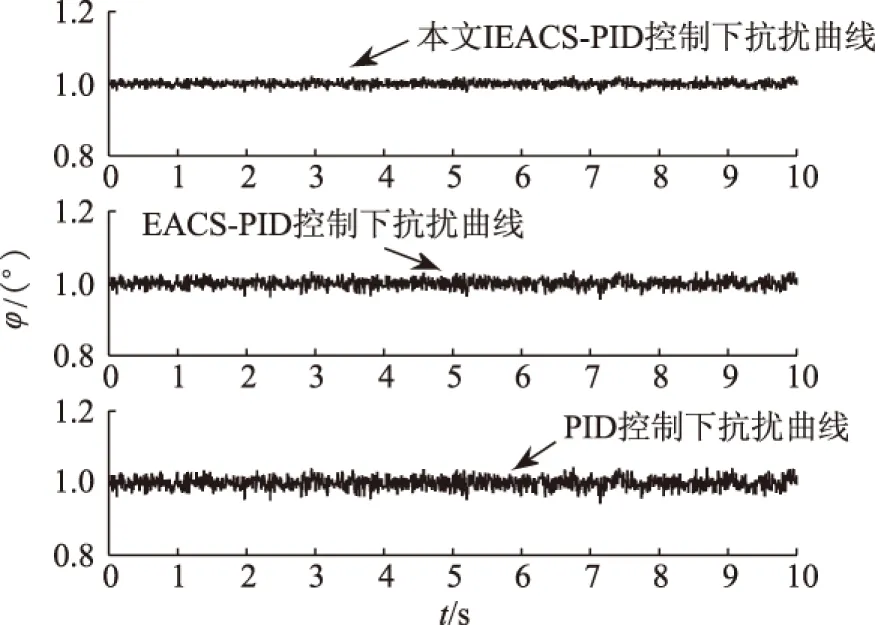


6 结语

