有限理性公理化建模研究述评

吴新林

(湖北第二师范学院 数学与经济学院， 武汉 430205)

有限理性公理化建模研究述评

吴新林

(湖北第二师范学院 数学与经济学院， 武汉 430205)

对有限理性的建模研究是近年来众多学者的一个研究热点。介绍了有限理性的基本概念，分别从对理性决策模型的改进和满意决策理论的建模两方面综述了有限理性下公理化建模的最新研究成果，并进行了归纳总结。

有限理性； 满意决策； 公理化建模

一、引言

近年来，对有限理性进行规范化研究和建模正成为决策科学领域的一个理论研究热点。对有限理性建模和规范化研究一般采取三种方法[1]：第一，补充传统的强理性模型，通常在效用函数中加入变量，或建立基于风险的期望效用函数；第二，基于动机、适应、认识三种智力过程，建立与实验结果保持一致的行为决策模型；第三，采用折中策略，将有限理性的约束与强理性模型的某些部分结合，建立有效的行为模型。

有限理性下的公理化建模是指从尽可能少的原始概念和不加证明的原始命题(即公理、公设)出发，按照逻辑规则建立有限理性下概念关系或数学模型的过程，从而对其它模型起到基础性的理论支持[2]。公理化建模更注重对决策过程的建模，强调的是理论框架，要求对有限理性进行严格的界定和定义，并且能够与完全理性的公理体系形成较为统一的整体框架。随着决策科学相关领域研究取得的进展和突破，对有限理性公理体系的建模研究逐渐成为国外学者关注的核心。现有的公理化建模方法一方面对有限理性决策人的认知能力的假设进行修正；另一方面通过修改或弱化VNM公理中的某些理性条件,从而建立有限理性行为公理体系。

二、有限理性的概念

Arrow在投票选举的具体实践中提出了有限理性的概念，他认为有限理性就是人的行为“既是有意识的理性，但这种理性又是有限的”[3]。诺思认为，人的有限性包含两方面[4]，一是环境的复杂性，人们面临的是一个复杂且不确定的世界，不确定性越大，信息就越不完全；二是人的计算能力和认识能力有限。Simon的有限理性内涵包含以下几方面[3]：一是，现实的环境是复杂和不确定的，而人的认知能力是有限的；二是，人的价值取向并不总是一成不变的，人的目标是多元化的；三是，短期记忆瓶颈使目标呈顺序趋势；四是，决策准则是满意的。由于有限理性是一个抽象的概念且成因复杂，故迄今尚没有一个学术上统一的界定和规范化定义，但仍有学者从不同角度对有限理性的概念进行了界定：(1) Kahneman和Tversky(1979)通过实验设计研究了人的决策行为[5]，结果发现现实中人的决策行为往往偏离经典决策理论的假定，总结出系统性的直觉与偏差以预测和解释决策过程中偏离理性的行为。Kahneman(2003)结合心理学试验，从行为经济学的角度给出了有限理性的内涵[6]:“bounded rationality is the study of deviations between human judgment and full rationality”(有限理性是研究人的完全理性与其判断之间的偏差)。该定义表明，不确定条件下的实际决策所产生的系统性偏差是导致有限理性产生的根本原因。(2) 决策者由于受到内部因素(如：注意力、记忆力等)和外部因素(如：时间、环境、信息搜集与加工等)的约束，所作出的决策不可能是完全理性的。Simon的“满意决策”可看成是某种成本约束条件下的最优化，基于此Arrow(2004)针对“有限理性”进行了重新定义[7]:“bounded rationality is ultimately optimization under constraints, and thus nothing but unbounded rationality in disguise——a common view among economists as well as some moral philosophers(有限理性是各种约束条件下的最优化，从而隐藏了无限理性——这是经济学家与一些道德哲学家普遍的观点)。” (3)决策者表现出“有限理性”特征的一部分原因是由于自身认知能力的不足，因此决策者对影响自身的不确定性因素需经历一定时间的思考和分析，Gigerenzer(2010)基于决策者的认知过程定义了有限理性[8]:“Bounded rationality is the study of the cognitive processes (including emotions) that people actually rely on to make decisions in the large world. (有限理性是研究人类在现实世界做决策所依赖的认知过程(包括情感))”

三位学者吸收了Simon的“有限理性”思想，以行为经济学为视角，从不同侧面对有限理性的内涵进行了界定。Kahneman强调决策过程中产生的系统性偏差是有限理性的成因；Arrow认为各种约束条件导致了有限理性的产生；Gigerenzer则将有限理性看成是对决策者认知过程的研究。尽管三种定义的表述各不相同，但均强调有限理性是一种过程理性，从而丰富和发展了行为决策理论的研究路线。

三、有限理性的公理化建模研究

(一)对现有理性模型的改进和完善

许多学者认识到EU理论及SEU理论对现实存在的偏离，为了能更好地解释这些悖论及非理性行为，对期望效用理论进行了扩展和修正，提出了更一般化的期望效用模型：如，Karmark(1978)提出的主观权重效用(Subjectively Weighted Utility)模型[9]，用决策权重取代线性概率，很好地解释了Allais悖论及Mac Crimmon和Larsson(1979) 的“共同比率效应”问题；Loomes和Sudgen(1982)提出的一种“后悔模型”[10]，将效用定义在个体对过去“不选择”结果的心理体验上(放弃选择后出现不佳结果感到庆幸，放弃选择后出现更佳结果感到后悔)，重新给出了线性期望效用函数的表达式。另外，Schmeidler(1989)的Choquet期望效用 (Choquet Expected Utility)[11]以及Gilboa和Schmeidler(1989)的多先验期望效用[12]等理论广泛应用于决策理论中。

另一方面，许多学者从VNM理性行为公理体系出发，对公理体系进行了补充或弱化。比较有代表性的成果如下：Aumann(1962)放弃了连通性公理，研究了如何用偏序在展望空间上表示效用理论，证明了基于独立性公理及弱连续性公理的线性效用函数的存在性，但效用函数的唯一性得不到保证[13]；Fishburn(1982)弱化了连通性公理，放弃了理性行为公理体系中有关非对称性、传递性等序特征的假设，提出了一组相应的公理体系，并为非线性效用理论的研究奠定了基石[14]；Ok(2002)用一个向量值效用函数来表示不完备偏好关系，并给出了不完备偏好关系的一个连续性表示定理[15]；Mandler(2005)检验了不完备偏好的选择理论基础，结果表明心理偏好的不完备性导致了显示偏好的非传递性但不会出现非理性的选择行为[16]。Eliaz和Ok(2006)通过减弱显示偏好弱公理，结合其他的一些假设条件，提出了个体选择的一个显示非劣弱公理，并基于该公理给出了不完备偏好关系下选择行为理性化的充要条件，最后通过考虑一些难以预料的意外情况扩展了选择范围，并添加了直观反映独立性公理的一个性质从而进一步完善了其理论框架[17]。Dagsvik(2002)针对有限理性和不确定性条件下的选择，从概率论的角度给出了连续性公理和两个独立性公理，提出了一般化的期望效用理论[18]。近年来，国内也有部分学者通过对理性行为公理体系进行了修改或弱化，例如，张明善等(1999)给出了有限理性下与完全理性行为公理平行的等价公理，直接揭示了效用函数存在的原理和直观意义[19]；郭耀煌(2003)针对VNM公理体系存在的局限性，通过弱化连通性公理，借助代数学中的格构建了与VNM公理体系平行的一套格序决策行为公理体系[2]。

通过比较国内外相关文献不难发现，许多学者(特别以Aumann、Fishburn等为代表的国外学者)从不同角度对理性行为公理体系进行了弱化或补充取得了一批有影响力的成果，此类研究成果主要集中在上世纪七、八十年代尤以国外学者突出但总体研究进展不够明显，主要原因在于：一方面此类研究注重严密的理论基础和体系的建立，放宽了经典决策理论中的许多严格假设条件导致建模难度较大；另一方面此类研究的方法主要采用数学或逻辑推理等理论工具，研究手段相对单一化。

(二)基于满意决策理论体系的建模

满意决策的概念是Simon在有限理性的基础上提出的。Simon认为满意型决策的本质是决策者作出的选择只需超过所确定的最低满意标准，在实际决策中，决策者在选择方案前不必搜索所有可能的替代方案，也没有必要对所有方案排序，而只需找到适合或超过目标值的方案即可，从而极大地提高决策效率，因而更能有效地指导实际生活中的决策。因此，基于满意决策的建模引起了许多学者的关注，取得了一批重要的成果。

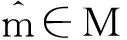
国内对于满意决策理论的研究多集中在满意度和满意解等概念的界定，如：任平(1983)借助模糊理论的工具对满意度和满意解的概念进行了描述，并着重对满意度的表示方法进行了研究[28]；靳蕃(1992)从评定模糊神经计算智能系统输出解的需要入手，给出了满意度的几种表示方法和相关的计算公式[29]。姚新胜等(2003)进一步提出了广义满意度的概念，分析了广义满意度、满意序、满意标准以及满意解等基本概念。构建了广义满意度原理的公理化体系，分析了广义满意度原理应用过程中满意解的获取、识别、转化等重要性质，并给出了满意度和满意水平之间的运算关系[30]。

基于满意决策理论的研究和修改或弱化完全理性公理体系是有限理性公理化建模研究的一个重要方面。此类建模注重的是基础理论研究，以数学理论、模糊理论或逻辑推理为主要工具，一方面对满意度、满意解及满意决策进行了相关研究；另一方面对经典的完全理性公理体系进行局部修改或条件弱化，从而建立有限理性下行为公理体系。这方面的研究尤以国外学者突出但研究进展不够明显，主要原因在于有限理性理论放宽了经典决策理论中的许多严格假设条件，导致建模难度加大。

四、结束语

20世纪90年代中期以来，有限理性的公理化建模是国外一些主流经济学家研究的一个热点，但由于有限理性的复杂性和隐性特征，公理化建模的研究一直无法获得较大的突破，至今没有一个得到普遍认同的公理体系。

本文从不同角度对有限理性下公理化建模的相关文献进行了梳理。对有限理性的公理化建模，学术上主要围绕以下两方面来进行探讨：一方面，通过对完全理性公理体系的修改或弱化，结合数理逻辑理论与决策理论等建立一套有限理性行为公理体系。另一方面，从有限理性的决策准则——满意决策的理论研究出发，借助优化理论等方法建立数学模型。建立一套系统的有限理性行为公理体系是目前决策理论研究的一个热点，这对于正确认识和理解现实经济现象、有效处理实际决策问题具有重要的理论意义和学术价值。

[1] Rubinstein A. Modelling bounded rationality[M]. Cambridge: MIT Press, 1998.

[2] 郭耀煌,郭强,刘家诚,等.格序决策[M].上海:上海科学技术出版社,2003.

[3] 李广海, 陈通. 现代决策的基石: 理性与有限理性研究述评[J]. 统计与决策, 2008, (3): 49-52.

[4] 方芳. 从理性和有限理性角度看决策理论及其发展[J]. 经济问题探索, 2005, (8): 64-67.

[5] Kahneman D, Tvernky A. Prospect theory: an analysis of decision making under risk[J]. Econometrica, 1979, 47(2): 263-291.

[6] Kahneman D. A perspective on judgment and choice: mapping bounded rationality[J]. American Psychologist, 2003, 58(9): 697-720.

[7] Arrow K J. Is bounded rationality unboundedly rational? Some ruminations. In: Augier M, March J G eds. Models of a man: essays in memory of Simon H A[M]. Cambridge, MA: MIT Press, 2004.

[8] Gigerenzer G. Moral satisficing: rethinking moral behavior as bounded rationality[J]. Topics in Cognitive Science, 2010, 2(3): 528-554.

[9] Karmarkar U S. Subjectively weighted utility: a descriptive extension of the expected utility model[J]. Organizational Behavior and Human Performance, 1978, 21(1): 61-72.

[10] Loomes G, Sugden R. Regret theory: an alternative theory of rational choice under uncertainty[J]. Economic Journal, 1982, 92(368): 805-824.

[11] Schmeidler D. Subjective probability and expected utility without additivity[J]. Econometrica, 1989, 57(3): 571-587.

[12] Gilboa I, Schmeidler D. Maxmin expected utility with non-unique prior[J]. Journal of Mathematical Economics, 1989, 18(2): 141-153.

[13] Aumann R J. Utility theory without the completeness axiom[J]. Econometrica, 1962, 30(3): 445- 462.

[14] Fishburn P C. The foundations of expected utility[M]. Holland: D. Reidel Publishing Company, 1982.

[15] Ok E A. Utility representation of an incomplete preference relation[J]. Journal of Economic Theory, 2002, 104(2): 429-449.

[16] Mandler M. Incomplete preferences and rational intransitivity of choice[J]. Games and Economic Behavior, 2005, 50(2): 255-277.

[17] Eliaz K, Ok E A. Indifference or indecisiveness? Choice-theoretic foundations of incomplete preferences[J]. Games and Economic Behavior, 2006, 56(1): 61-86.

[18] Dagsvik J K. Choice under uncertainty and bounded rationality[D]. Discussion Paper, 2005.

[19] 张明善, 何德全，等. 有限理性行为公理的等价公理[J]. 管理工程学报, 1999, 13(2): 63-64.

[20] Mesarovic M D, Takahara Y. On a qualitative theory of satisfactory control[J]. Information Sciences, 1972, 4(4): 291-313.

[21] Matsuda T, Takastu S. Characterization of satisficing decision criterion[J]. Information Sciences, 1979, 17(2): 131-151.

[22] Matsuda T, Takastu S. Algebraic properities of satisficing decision criterion[J]. Information Sciences, 1979, 17(2): 221-237.

[23] Goodrich M A. A theory of satisficing control[M]. Provo: Brigham Young University, 1996.

[24] Tyson C J.．Cognitive constraints, contraction consistencyand the satisficing criterion[J]. Journal of Economic Theory, 2008, 138(1):51-70.

[25] Papi M. Satisficing Choice Procedures[J]. Journal of Economic Behavior & Organization, 2012, 84(1): 451-462.

[26] Masatlioglu Y, Nakajima D, Ozbay E Y. Revealed attention[J]. American Economic Review, 2012, 102(5): 2183-2205.

[27] Masatlioglu Y, Nakajima D. Choice by iterative search[J]. Theoretical Economics, 2013, 8(3): 701-728.

[28] 任平. 优化理论中的令人满意准则[J]. 模糊数学, 1983, (4): 111-112.

[29] 黄洪钟, 姚新胜, 周仲荣. 满意度原理研究与应用的现状与展望[J]. 控制与决策, 2003 , 18(6): 641- 645.

[30] 姚新胜, 黄洪钟, 周仲荣. 广义满意度原理及其特性分析[J]. 西南交通大学学报, 2003 , 38(6): 712- 716.

责任编辑：肖 军

A Summary of Research on Axiomatic Modeling of Bounded Rationality

WU Xin-lin

(School of Mathematics and Economics, Hubei University of Education, Wuhan 430205, China)

Modeling bounded rationality is a hot research in recent years. In this paper, the concepts of bounded rationalities are defined. Some latest research results about axiomatic modeling of bounded rationality are summarized from modified rational decision models and modeling satisfying decision respectively.

bounded rationality; satisfying decision; axiomatic modeling

2016-10-25

湖北省教育厅科学技术研究项目(Q20153002)

吴新林(1981-)，男，湖北黄冈人，讲师，博士，研究方向为决策理论与方法。

C934

A

1674-344X(2016)12-0031-04