朱载堉的生平及其数学成就
——纪念朱载堉诞生480周年
戴念祖
(中国科学院自然科学史研究所,北京 100190)
朱载堉的生平及其数学成就
——纪念朱载堉诞生480周年
戴念祖
(中国科学院自然科学史研究所,北京 100190)
王子朱载堉是明代数学家、音乐家。他的一生跌宕起伏:18年受难,14年著书立说,11年雕版印书,15年让爵。他的数学成就有:求解几何数列,不同进位的数字换算,珠算开方等。这些数学工作是他创建等程律的基础。长期以来,某些西方音乐史家怀疑朱载堉的数学能力。文章重新评说朱载堉的数学成就及其与乐律的关系,以此纪念朱载堉诞生480周年。
朱载堉 几何数列 珠算开方 等程律
随着西方17、18世纪科学革命和工业革命的伟大成功,中国古代科学家及其科学成就鲜有能在这两大革命之后而独占鳌头者。唯有明代王子朱载堉(1536~1611)所创建的十二等程律,迄今仍在音乐舞台上熠熠生辉。正如文学家、语音学家刘半农(1891~1934)所言,朱载堉的等程律“直到现在谁也不能推翻它、摇动它;他所用的算法,直到现在还是照样去做;他算出来的数字,直到现在还是直抄了用”[1]。然而,近几十年来,一些西方学者怀疑朱载堉的数学能力[2],中国数学史著作对其解几何数列的数学成就似乎迄今未有称赞者。本文就此作一通俗解说,明其道理,识其金玉,并以此纪念朱载堉诞生480周年。
1 朱载堉的生平
朱载堉是明朝开国皇帝朱元璋的九世孙。更直接一点,是明仁宗朱高炽的七世孙。仁宗长子朱瞻基袭帝位,是为宣宗;仁宗次子朱瞻峻赐“郑王”。“王”是爵位,“郑”是封地、又称“藩国”。郑王藩国在怀庆府(今河南沁阳)。“郑王”传至仁宗六世孙朱厚烷(1518~1591),即朱载堉之父。朱载堉10岁(1545)册封“世子”爵,人称“王子”。论辈份,明神宗朱翊钧(即万历帝,1573~1620年在位)称朱载堉为“宗伯”。[3]
嘉靖帝醉迷道教,大兴土木建斋醮,以致不理朝政。嘉靖二十七年(1548),朱厚烷上疏,劝帝修德讲学,“以神仙土木为规谏,语切直”[4]。也有文献说,朱厚烷在《上进表》中自称“弟,不称臣”[5]。嘉靖帝览奏大怒。又厚烷之族叔伯间争嫡夺爵而诬告厚烷有叛逆罪。因之,朱厚烷被革除国爵,并被囚禁于老家安徽凤阳。朱载堉受此牵连,被革除世子爵。他“痛父非罪见系,筑土室宫门外,席藁独处”([4],3628页)。后又曾上少林寺,拜僧人松谷为师。直到嘉靖帝薨,穆宗继位,厚烷父子才得以平反,复国爵。这次苦难经历18个年头。*史书[4]载19年,不确。
复爵返国后厚烷指导载堉习乐律,并令其研究返宫问题。他说:
仲吕顺生黄钟,返本还元;黄钟逆生仲吕,循环无端。实无往而不返之理,笙琴互证,则知三分损益之法非精义也。[7]
众所周知,若以三分损益算律,虽仲吕顺生黄钟,但不能返元,尚有一音差;而黄钟也不能逆生仲吕,只能逆生林钟。要解决厚烷提出的这个问题,只有创立新的律制。这就让朱载堉整整忙活了14年,即从隆庆元年(1567)到万历九年(1581)创建“新法密率”为止。朱载堉称谓的“新法密率”即今天大家熟知的十二等程律。万历九年,朱载堉为其著《律历融通》作序,该书附录《音义》篇中道出了“新法密率”的五度相生和四度相生的数学方法。这就是其父令其完成的返宫的数学和音乐学难题。值得注意的是,在这14年间,朱载堉完成了《乐律全书》中乐、舞、算方面的大部分著作。
从万历二十三年(1595)始,朱载堉在王府内雕刻《乐律全书》。到万历三十四年(1606),《乐律全书》雕版、印刷、装帧完毕。前后又11年。随即,朱载堉上进四部《乐律全书》刻本,并得到了万历帝称赞:“具见留心乐律,深可嘉尚。”[8]
万历十九年(1591)正月郑王朱厚烷薨。六月,王子载堉即“以微恙辞管府事”[9],实则为辞爵假之以病。万历二十一年(1593),载堉上疏,要“让国爵载玺”。载玺是载堉叔伯兄弟。当年正是载玺的祖父诬告载堉的父亲有叛逆罪,以致厚烷被囚禁。可见王子载堉的气度非同寻常。经过反复上疏,最终于万历三十四年(1606)获万历帝准允,将爵位让于载玺。载堉因此获万历帝赐赦表彰,给禄建坊,以示优贤之义([6],65~72页)。从万历九年到三十四年的整15年7疏,载堉才将爵位让出。其志之坚,其情之固,可赞也。清代诗人沈德符(1578~1642)称颂朱载堉“真天潢中异人也。”[5]
让出国爵后,朱载堉迁居怀庆城郊,自称道人,超然于人世间名禄红粉之外,过着箪食瓢饮的生活。早晚邀上三五个山野好友,“一人吹律,一人弹琴,一人击缶而歌。余亦自歌,互相倡和,而乐在其中矣。”([6],74页)此情此景,与今日公园一角老人吹拉弹唱度晚年相似。
万历三十九年(1611)四月初七日(5月18日),朱载堉卒于怀庆城外九峰山下,年76岁。
2 数学成就
2.1 构架并求解几何数列
众所周知,在五度律(或三分损益律)中,将起始音(设为C)的频率累乘以3/2(或其弦长累乘以2/3)12次之后,得到第十三个音(C1)不刚好是起始音(C)的倍数。这在音乐学上称为“不能返宫”。在西方音乐学术语中,这意思是五度圈不能成为“一个闭合的圆”。五度、八度是完全悦耳、协和的音程,为何12个五度之后产生的八度却不纯正了呢?数学计算在哪个节点上出了问题?音乐学上千年的返宫难题,直到明代朱载堉决心抛弃五度律,另辟新径,才得到完满解决。

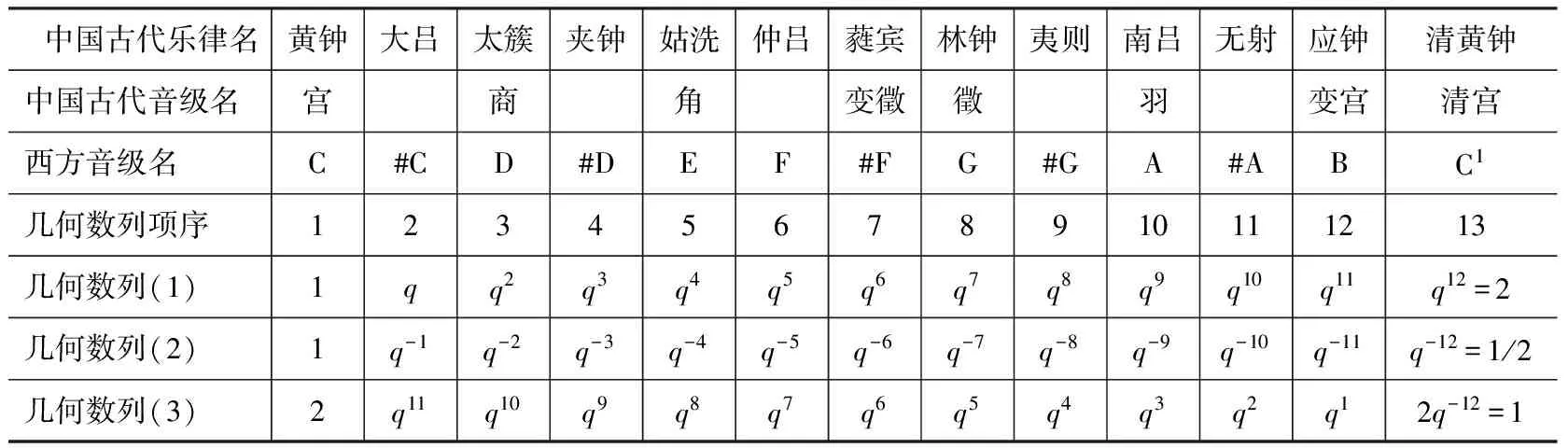
表1 乐律名称与几何数列对应表
注意:我们将表1中几何数列(3)简单列示如下:因为q=21/12,所以大吕是由黄钟2除以q一次得出的,即大吕为2/q=q11;蕤宾是由黄钟2累除q六次得出的,即蕤宾为2/q6=q6;南吕是黄钟2累除以q九次得出的,即南吕为2/q9=q3;应钟是黄钟2累除以q十一次得出的,即应钟为2/q11=q1。
表1中几何数列(2)和(3)适用于乐律的弦长比值,从1到1/2或从2到1的几何数列对应于弦长愈来愈短,乐音愈来愈高;几何数列(1)适用于乐律的频率比值,若将(1)用于弦长比,则要将表1中第1横栏的音高顺序颠倒为之。如此,朱载堉称几何数列(3)、(1)和(2)分别为倍律、正律和半律。
联系表1,就容易解读朱载堉在《律吕精义内篇》卷1《不用三分损益》中所写下的文字:
新法算律与方圆皆用勾股术。其法本诸《周礼·栗式为量》“内方尺而圆其外”。“内方尺而圆其外”,则圆径与方斜同。知方之斜则知圆之径矣。
度本起于黄钟之长,则黄钟之长即度法一尺。
命平方1尺为黄钟之率,东西10寸为勾,自乘得100寸为勾幂;南北10寸为股,自乘得100寸为股幂。相并共得200寸为弦幂。乃置弦幂为实,开平方除之,得弦1.4142 1356 2373 0950 4880 1689尺,为方之斜,即圆之径,亦即蕤宾倍律之率。以勾10寸乘之,得平方积141.42 1356 2373 0950 4880 1689寸,为实,开平方除之,得1.1892 0711 5002 7210 6671 7500尺,即南吕倍律之率。仍以勾10寸乘之,又以股10寸乘之,得立方积1189.2 0711 5002 7210 6671 7500寸,为实,开立方除之,得1.0594 6309 4359 2952 6456 1825尺,即应钟倍律之率。盖十二律黄钟为始,应钟为终,终而复始,循环无端,此自然真理,犹贞后元生,坤尽复来也。是故各律皆以黄钟正数10寸乘之为实,皆以应钟倍数10.5946 3094 3592 9526 4561 825寸为法除之,即得其次律也。安有往而不返之理哉?旧法往而不返者,盖由三分损益算术不精之所致也。是故新法不用三分损益,别造密率。*为便于现代人更容易看得清楚,将原文的汉字数字改为了印度—阿拉伯数字。




朱载堉算得q是一个25位数字,即

从数学上看,这长段文字实际上就是在1与2之间设定的一个由13项构成的几何数列,求出这个几何数列的公比数(即应钟倍律弦长),问题就解决了。在音乐学看来,任一起始音的弦长,“皆以应钟倍数……为法除之,即得其次律也”。如此,朱载堉建成了十二等程律,完成了千年的返宫之愿。

应当怎样评价朱载堉这一数学成就?我们知道,在乐律史上,凡有重大贡献的乐律学家,也必定是个数学家。朱载堉在《算学新说》弁言中说,“臣所撰新说凡四种:一曰律学,二曰乐学,三曰算学,四曰韵学。前二者其书之本原,后二者其书之支脉,所以羽翼其书者也”。也就是说,他将数学看作是他创建一种崭新律制的“翅膀”。在数学思维上,朱载堉的工作至少突破了前人常以一个自然整数为起点而构成几何数列的范式,如以3为公比数的几何数列即1、3、9、27、81等等。要在相邻两个自然整数如1和2之间构架一个由13项组成的几何数列,这是朱氏的乐律研究为中国数学史上提供的有关等比数列的新实例。中国古代数学史上真正的几何数列例题极少。[11]在已知首项、末项和项数,而要求解这样几何数列的数学题目,在朱载堉之前似乎未曾有过。再者,朱载堉将2的开十二次方运算到25位数,且准确无误[12],确实令人惊叹。此前的中外数学史上,还未有过如此多位数的计算数字。20世纪90年代之前的普通电子计算器也只有10位数而已。

2.2 在由四项构成的几何数列中,提出第二、三项的求解法


图1 《算学新说》中的乐律计算(其中


图2 圆内接正方形(设a=b=1,则;设c=1,则
由以上的计算,在图1的几何数列中,就已知它的首项(倍蕤宾)、末项(正蕤宾)和他们的中项(正黄钟)了。对于这个几何数列问题的解,朱载堉在《算学新说》中写道:
第四问:以黄钟正律乘蕤宾正律得平方积……*本文略其具体积值。下文同。开平方所得即夹钟正律……*删略25位数字答案及其算草。下文同。
第五问:以黄钟正律乘蕤宾倍律得平方积……开平方所得即南吕倍律……
这两问是求几何数列的等比中项。第四问的“正夹”即是“正黄”和“正蕤”之间7项组成的等比中项;第五问的“倍南”是“倍蕤”到“正黄”的中项。从这两问中不难看出,等比中项为首末两项之积的平方根。这是完全正确的。
《算学新说》中还计算了图1中的大吕和倍应钟两项。它写道:
第六问:置夹钟正律以黄钟再乘,得立方积……开立方所得即大吕正律也……
第七问:置南吕倍律以黄钟再乘,得立方积……开立方所得即应钟倍律也……
由图1可见,第六问所求的“正大”是“正黄”到“正夹”的四项组成的第二项;第七问所求的“倍应”是“倍南”到“正黄”的四项组成的第三项。在由四项组成的几何数列中,求解其第二、三项的方法,朱载堉一一列举清楚了。仿此,就可以解出图1中其余各项。一个13项的几何数列得以求解,也就在八度内解出了它的各个乐律的音高数值。
对于朱载堉的这一数学成就,在中国数学史上似乎并未引起人们重视,迄今尚未有一本数学史著作对此作出叙述。这原因大概是《算学新说》中的数学与乐律计算紧密相关,乐律学的内容让人们不能一眼识破其数学本质。
2.3 珠算开方
算盘的发明和应用在中国古代有较长的历史。起初人们只用它做加减乘除的四则运算。珠算开方朱载堉不是最早的一个,但他却是最接近近代数学方法的一个。朱载堉一生中,计算历法、乐律,都是用珠算完成的。在他的乐律研究中,留下了7位数、9位数、18位数,甚而多达25位数的计算数值而无一错误,这不能不归于他用了当时最先进的计算工具算盘的缘故。
朱载堉在其著《算学新说》的弁言“初学凡例”中写道:
凡学开方,须造大算盘,长九九八十一位,共五百六十七子,方可算也。不然,只用寻常算盘,四五个接在一处算之,亦无不可。其算盘梁上贴纸一长条,上写第一位、第二位等字样,使初学易晓也。
该书第六问之弁言也写有“初学立方凡例”,指出“凡开立方,将算盘梁上贴一纸条,写千百十寸、百十分、百十厘、百十毫、百十丝、百十忽、百十微、百十纤之名,至于纤以下位数,不立名色,只隔二位画一圈,使开方除实不错耳。”
这些文字说明了计算出25位数的算盘所需档位和注意事项。朱载堉还详细注明开方口诀,举出不少例题算草。一些数学史著作对此也有所演释([11],577页)。*1991年,笔者曾在一次全国性律学讨论会上,目睹天津一会计师冯文坤女士在81档大算盘上为众人作开方演算,速度甚快。本文在此仅评述朱载堉开方运算的历史地位。
《算学新说》刻版完毕于万历三十一年(1603),人们以此确定朱载堉完成珠算开方的年限并不确切。其理由如下:
(Ⅰ)1603年既是雕刻完毕《算学新说》,也是完成雕版《乐律全书》整套书的时间。《乐律全书》中诸本书,唯此留下时间记述,其用意即在于此。此后便是《乐律全书》的印刷、装帧了。
(Ⅱ)除了《圣寿万年历》和《万年历备考》二书是在万历二十二年(1595)之前一、二年完成之外,《乐律全书》中其余乐、舞、历、算诸书都在《律历融通》作序之时(万历九年,1581年),甚至更早时候已经完成。其证据如下:
(1)《律吕融通》书末附《音义》一篇,该篇文字为注释该书中一些名词术语和数学方法,其中写道:
大抵不用三分损益,而用勾股之术及开立方之法求之所得也。是以隔八隔六、循环无端,上下相生,首尾一贯,以证往而不返之说为非。是盖二千余年之所未有,实自我朝始耳。恐后世儒者疑,故略释之,其详则见诸《律吕精义》云。
这里所说的“勾股之术(开平方之法)”、“开立方之法”,朱载堉是用珠算做的。不仅如此,朱载堉还指出,欲知《律历融通》内容之详者,请读者“见诸《律吕精义》”。后者是《乐律全书》中最为重要的一本著作,可见它完成于《律历融通》之前。也即珠算开方的运算完成于1581年之前。
(2)《律学新说》(作序于1584年)的初稿是《律学四物谱》。所谓“四物”即黍、度、量、权。《律学四物谱序》尚留在《律学新说》的《附录》中。该序文中写道:
尝撰《黍谱》、《度谱》、《量谱》、《权谱》,各卷帙不等,总若干万言,今摘其要合为一书,名曰《律学新说》,而以所问所答冠其篇名。《四物谱》原稿文烦而考据详密,后乃删烦摘要,更名《律学新说》,成书以进。校其原稿,特十分之一耳。兹因暇日重校原稿,见此序文,不忍弃去,是故续刊附于简末,使览者知作者初意。
这段文字充分说明《律学新说》原稿本早在1584年作序之前已完成。可见朱载堉珠算开方的工作也并非完成于《算学新说》雕版完毕的1603年。
令人惊讶的是,《律学新说》的“序”文中还写道:关于律管的周径计算问题,“已见《律书》及《算学新说》,兹不复载,但载各律长短并内外周径图样”。这里,明白地告诉读者:《律学新说》中的相关问题详见《算学新说》一书。前者又是早年旧稿压缩而成。可见《算学新说》一书在1581年之前已完稿是毫无疑问的。
(3)在《律历融通·音义》中还有珠算开方的直接证据。《音义》写道:
先置黄钟十寸在位。下生者五亿乘之为实,七亿四千九百一十五万三千五百三十八为法,除之得林钟;就置所得全数在位,上生者十亿乘之为实,仍以前法除之,得太簇。余律仿此,乘除十二遍,则返本还元。此系新法,与古法不同。
所谓“在位”是将要计算的数字拨在算盘的相应档位上。这段文字被称之为十二等程律的五度相生[13]。它是必须在完成如表1中的三种几何数列的任一种演算之后,才能进一步推出它的快捷计算法即五度相生法。在这段文字之后还有十二等程律的四度相生的简捷算法,本文不再详引。它们充分证明,珠算开方的运算,至少在公元1581年之前朱载堉已相当娴熟了。
或许,上述考证是多余的。万历九年十月(1581年11月),《明神宗实录》记载,“郑王厚烷有疾,世子载堉亦久病”([9],万历九年十月已未)。而这一年,载堉拟将其完成的乐、舞著作进献宫廷,朱厚烷“恐有缺误,未敢遽行,仍付臣(载堉)订正之”,不料,“值臣(载堉)宿疾举发,连年未疗,由是迁延,未曾进献”([8],2~96上栏)。自然,这些乐、舞著作包括了《算学新说》在内。当然,它们都是手稿本,尚未雕版印刷。中国古代的著作,虽然一般可以用其序文时间或刻版时间定其创作年代。然而,类似朱载堉的著作,当是中国书籍史上一特例[14- 15],不能以其书作序或雕版的时间论其创作的岁月。
由上考证,充分证明《算学新说》完稿于1581年之前。之前多久?亦难断论。只能说,在其父朱厚烷复爵返国(隆庆元年,1567)到《律历融通》作序(万历九年,1581)的时间内,朱载堉彻底地掌握了珠算开方,并以此在世界上首创十二等程律。
在中国数学史上,徐心鲁《盘珠算法》于1573年初刊,柯尚迁《数学通轨》于1578年刊刻。但此二书均未涉及珠算开方。余楷《一鸿算法》于1584~1585年刊刻,据说其中有开方计算。其后便是程大位的《算法统宗》,于1592年刊刻([11],553,556,557,559页)。朱载堉是在1581年之前完成的《算学新说》,因此,理应重视它在中国数学史上的历史地位。据研究,在珠算史上第一个做开方运算的是明代王文素,他于1524年撰《算学宝鉴》,其中述及珠算开方。[16]朱载堉和王文素不同的是,前者的方法接近现代,后者的方法是传统的继承。
在珠算史上,尚需强调的是,人们常常将算盘看作商业计算工具。而从朱载堉如此之早运用珠算开方并计算乐律的情形看来,算盘确曾是人们进行学术研究的计算工具。
朱载堉还有一项数学工作在数学史上也是有影响的,即他所做的关于九进制和十进制的小数换算([14],190页)。这项工作已被数学史著作所重视([11],598页),本文不再重复。
朱载堉在《算学新说》弁言中曾如此评价自己的“新说”:
谓之新说,何也?且如周径幂积相求之类,旧则疏而新则密;平方不用商除,立方不显廉法之类,旧则繁而新则简;旧以勾股为末,专明九章,新以勾股为首,专明律历。此其异也。余则文虽小异,要亦殊途同归者也。
这三条自我评价不完全正确。第一条,言及周径幂积相求一事,其要在于圆周率取何值?朱载堉的圆周率是这样得到的:设一个正方形的边长为9寸,他以片纸或线条移量其外接圆的圆周为40寸([6],265页)。因此,其圆周率值为

其中的第二条即“平方不用商除,立方不显廉法”的评价是恰当的。这是朱载堉在数学上的一项重要成就。其数学思维更接近于现代而远离古代。故而,他说“旧则繁而新则简”并不夸张。至于第三条,仅仅是勾股术或开方术用在不同学科、不同对象上之分别。值得称颂的是,朱载堉找到一种数学方法解决了乐律返宫,从而在音乐上开天辟地地创造了一种新律制,并影响至今不息。这是他的最大贡献!
1 刘复. 十二等程律的发明者朱载堉[C]//庆祝蔡元培先生六十五岁论文集//国立中央研究院历史语言研究所集刊外编(第1种).北平:国立中央研究院,1933.274~310.
2 Kuttner F A. Prince Chu Tsai-Yu’s Life and Work—A Re-evaluation of His Contribution to Equal Temperament Theory [J].Ethnomusicology, 1975, 19(2):163~205.
3 王铎. 郑端清世子赐葬神道碑[M]//戴念祖. 天潢真人朱载堉. 郑州:大象出版社,2008.335~338.
4 张廷玉,等. 明史·诸王列传四[M]. 北京:中华书局,1974.3627.
5 沈德符. 万历野获编·郑世子让国[M]. 北京:中华书局,1959.119.
6 戴念祖. 天潢真人朱载堉[M]. 郑州:大象出版社,2008.55~56.
7 朱载堉. 律吕精义·序[M]//任继愈主编. 中国科学技术典籍通汇·物理卷. 第2册. 郑州:河南教育出版社,1995.2~98页下栏.
8 朱载堉. 进律书奏疏[M]//任继愈主编. 中国科学技术典籍通汇·物理卷. 第2册. 郑州:河南教育出版社,1995.2~97页下栏.
9 神宗实录[M]. 第53册. 卷117//明实录. 台北:中央研究院历史语言研究所, 1967.2209.
10 Dijksterhuis E J.SimonStevin:ScienceintheNetherlandsaround1600[M].The Hague: Martinus Nijhoff, 1970.21~38.
11 郭书春. 中国科学技术史·数学卷[M]. 北京:科学出版社,2010.258,577~578.
12 沈柏宏教授用高速电脑证明中国人最早发明十二平均律[J]. 吕国璋,译. 乐苑,1986,(15):19.
13 戴念祖. 从传统音乐学和数学角度看朱载堉创建等程律的思维[J]. 中国音乐学,2014,(4):20~25.
14 戴念祖. 朱载堉——明代科学和艺术巨星[M]. 北京:人民出版社,1986.91~96.
15 李纯一. 朱载堉十二平均律发明年代辩证[J]. 音乐研究,1980,(3): 33~34.
16 劳汉生. 珠算与实用算术[M]. 石家庄:河北科学技术出版社,2000.299~307.
Prince Zhu Zaiyu’s Life and His Achievements in Mathematics:The 480th Anniversary of the Birth of Zhu Zaiyu
DAI Nianzu
(InstituefortheHistoryofNaturalSciences,CAS,Beijing100190,China)
Prince Zhu Zaiyu was a mathematician and musician during in Ming Dynasty (1368-1644). His life went through many ups and downs. He suffered for 18 years, wrote for 14 years, did block printing for 11 years, and gave up his royal position to another brother for 15 years. His achievements in mathematics consist of the calculation of geometrical series, the conversion of numbers of different carries, the extraction of roots using Chinese ancient abacus, and so on. These mathematical works are the basis of the equal temperament founded by him. Certain historians of music in the Western doubted Zhu Zaiyu’s mathematical ability for a long time. The paper re-evaluates Zhu Zaiyu’s mathematical achievements and expound the relation between them and musical tone.
Zhu Zaiyu, geometrical series, extraction of a roots by Chinese ancient abacus,Twelve tone equal temperament
2016- 01- 12;
2016- 09- 09 作者简介:戴念祖,1942年生,福建长汀人,中国科学院自然科学史研究所研究员,主要研究方向为中国物理学史。
N092∶K82
A
1000- 0224(2016)04- 0417- 10

