如何理解计量经济学中的假设检验

陈清华，郭金忠，袁 强

(1.北京师范大学 系统科学学院，北京 100875；2.新疆大学 经济与管理学院，新疆 乌鲁木齐，830046；3.北京师范大学 经济与工商管理学院，北京 100875)

(上为任意分布情况，下为标准正态分布情况)

如何理解计量经济学中的假设检验

陈清华1，郭金忠2，袁 强3

(1.北京师范大学 系统科学学院，北京 100875；2.新疆大学 经济与管理学院，新疆 乌鲁木齐，830046；3.北京师范大学 经济与工商管理学院，北京 100875)

假设检验是整个计量经济学中的主要内容，也是数理统计中的重要部分。但目前在计量经济学相关教科书中和教师的教学过程中，往往容易侧重于参数估计方法的介绍，而在假设检验方面的分析不够深入，相关的背景和逻辑交待不充分，使得同学们不能真正理解假设检验，最后造成对整个计量经济学学习和应用的障碍。论文联系其他背景材料，重新整理有关假设检验的逻辑体系，扩大知识面，剖析、展示假设检验相关各个知识点的逻辑和联系，旨在促进学生们对计量经济学中假设检验思想的真正理解，促进真正的计量经济学教学改革。

计量经济学；假设检验；教学改革

一、问题的提出

自20世纪70年代末80年代初，计量经济学开始进入中国。经过30多年的发展，计量经济学模型已经成为经济理论研究和实际经济分析的一种主流实证方法[1-3]。据统计，2007年《经济研究》发表的文章中以计量经济学模型方法作为主要分析方法的论文占53%，2009年《管理科学》发表的文章中此类文章占比达到55%[1]。这个成就与我国在教学方面对计量经济学的重视是分不开的。1998年7月，教育部高等学校经济类学科专业教学指导委员会讨论并确定了高等学校经济学门类各专业的8门共同核心课程，其中就包括“计量经济学”。根据李子奈等人的调查，早在2006年，设置经济类和管理类本科专业的高校中分别有98%及60%以上的学校开设了该课程[2]。目前，一些相关的教育改革在全国范围内不断进行[4-6]。

与计量经济学的应用蓬勃发展相对应，我国的计量经济学应用研究中，问题和错误也大量存在[1]。其中一个非常典型的表现就是一些作者在回归得到参数的估计之后就进入结论部分，缺乏必要的假设检验过程，甚至连估计量的方差估计都没有给出。究其原因，实际上反映了作者对于假设检验理解的欠缺。这个与教学中同学们的反映是一致的。在笔者的教学过程中，学生们对于参数估计的计算没有什么问题，最大的障碍在于假设检验部分的理解，他们认为假设检验部分比较抽象，难以理解t检验是怎么来的，不能明白为什么估计真实参数的置信区间和点估计的置信区间形式上是如此一致。为此，本文就计量经济学的基本知识[7-8]，结合其他背景，对假设检验的重点部分进行梳理阐释，让它更加清晰而有条理。

二、假设检验的科学性——可证伪性

什么是科学的标准，长期以来并没有统一的说法，直到波普尔科学哲学思想的提出。波普尔(Karl Popper)提出的对科学的判断标准即使目前仍然存在反对的声音，但它无疑已成为一种经典之论。在波普尔的词典里，“科学”不是“有意义”或“有价值”的同义词，更不是“正确”或“真理”的同义词。他强调，科学理论都只是暂时的、尚未被证伪的假设[9]，更是否定了将科学等同于真理的迷信。科学必须留下破绽，让别人有反对它、说它错误的机会。从这个角度来看，哲学、神学往往都不是科学的。

自然科学中，特别是物理，充满了可证伪性。以牛顿(Isaac Newton)力学为例，牛顿第一运动定律中有表述：任何物体在不受任何外力的时候，总保持匀速直线运动状态或静止状态，直到有作用在它上面的外力迫使它改变这种状态为止。不管我们现在是否能做到一个物体不受力的情况，但是我们总是有机会在有更高超的手段的时候去检验它是否说错了。再有一个例子，就是爱因斯坦广义相对论指出重力会造成时空弯曲，1911年，爱因斯坦(Albert Einstein)首次计算了光线在引力场中的偏折，并于1915年进行了完善，他预测了远处恒星的光线经过太阳附近时的偏折量。如果在某次实验观测没有发现光线被偏折的情况下，显然这个理论很容易被证明错误。但1919年5月29日日食时在巴西的索布拉尔的观测和理论预测符合得较好[10]。从此，广义相对论为更多的人所接受。

理论提出后来进行实验验证的过程本质上就是一个假设检验过程，科学的理论必须让观测者有机会去反对原来的假设。我们在计量经济学中也是如此做的：在一次观测获得原假设情况下非常罕见的事情时候，观测者有权利质疑原假设的正确性。毫不夸大的说，假设检验因为具有这样的科学性而被广泛应用于各个学科，包括社会统计学等。假设检验是计量经济学中具有可证伪性的部分，从而让计量经济学在整个经济学体系中表现出科学性，最终使得这个学科具有无法替代的地位。朱家祥教授也曾指出：“我同意计量经济学是证伪而不是证实的观点。”。虽然有其他学者认为，在方法论上计量经济学既不是完全的证伪主义,也不是完全的实证主义,而是两者的综合。但假设检验的可证伪性是普遍承认的[1]。

假设检验和数学上反证法的思想也是一致的，即先做出假设，然后在假设的基础上得到矛盾的结果，从而最终有可能去推翻原假设。大家知道，数学上的反证法是非常有说服力的。

三、假设检验的本质——通过样本估计总体

假设检验是联系总体和样本纽带。假设检验的过程是这样：首先对于总体的性质有个原假设(其对应的为备择假设)，然后从总体中获得一些样本，对这些样本进行观测，根据观测结果来决定在一定程度上是否拒绝原假设。检验的结果有两个：拒绝原假设或者不能拒绝原假设。要注意，检验的结果不能认定原假设为真，最多是不能拒绝。检验结果也是针对总体的。

样本来源于总体。一般而言，我们会更加关注的总体的性质，而不是样本的性质。对于总体的把握要比对样本的把握有意义得多。因为总体的性质是最根本的，它决定已经抽出的样本乃至将来可能抽出的样本的特征。总体才具有稳定不变的特性，样本的个体性质是千变万化的，总体的稳定性质往往被个体的一些随机特性所掩盖。认清一个人的本质比纠结于他做的一件琐事要有意义得多。

正因为如此，假设检验比参数估计要重要。但在教材上我们很容易发现参数估计部分写得要多一些，而假设检验部分倒写得少。其原因我想可能是假设检验的思想比较简单，不需要用长篇幅的学术语言来表达，而估计部分有一些不同的估计方法：包括普通最小二乘法，矩估计法和极大似然估计方法，这些方法都有丰富的思想和技术细节需要展示。

参数估计只是样本数值的一个计算结果，总体的性质才是最重要需要最终把握的。参数估计只是为了后面的假设检验为基础。应该清楚，参数估计的大小是没有意义的，因为真实的参数可能离开它很远，必须通过假设检验的手段来对真实参数的进行判断。

四、假设检验的前提条件——显著性水平

我们所有讨论的东西都是在概率意义的进行的。通过样本的性质得到的总体情况也是在一定概率意义上的，体现在假设检验上就是显著性水平，或者由样本计算得到总体某个参数的置信区间。

在假设检验中会涉及到两类错误：第一类错误和第二类错误。第一类错误也称为α错误，是指当原假设(H0)正确时，而拒绝H0所犯的错误。第二类错误也称为β错误，是指原假设错误时，反而做出结论不能拒绝原假设的情况。

例如这个命题是正确的：犯罪分子有95%以上的概率都是金黄色头发。这个命题等价于如果某个人X是犯罪分子，则X有金黄色头发的概率大于95%。

这时候，我们有原假设H0: X是犯罪分子，我们通过对他头发颜色的观测来决定是否拒绝原假设。则不管我们观察到X的头发颜色而做出是否拒绝原假设的决定都有可能犯错误。

第一类错误：X是犯罪分子，但头发不金黄，我们拒绝了原假设。

第二类错误：X不是犯罪分子，但头发金黄，我们没有拒绝原假设。

此时，我们对于犯第二类错误的概率是不清楚的，因为普通人的头发颜色如何并没有交代。但犯第一类错误的概率是知道的，因为犯罪分子有95%以上的概率都是金黄色头发，也就是只有5%以下的概率头发不是金黄的，所以我们发现X头发不是金黄的而拒绝原假设时，可能犯错误，但这个犯错的概率是5%以下。

假设检验中的显著性水平就对应着对犯第一类错误的概率控制。如果我们要求犯第一类错误的概率更低，则对应着更小的显著性水平。而大的显著性水平意味着更不严格的要求。

五、最粗略的假设检验——契比雪夫不等式

契比雪夫(Chebyshev)不等式体现了期望和方差的联合作用效果，表明方差可以在概率意义上控制样本点偏离总体期望的距离。具体表达式如下：

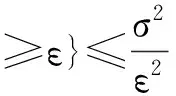
(1)

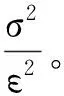
这个定理的证明也很简单，可以直接写在下面：

(2)

其中f(x)为该分布的概率密度函数。

要明确地是，有了契比雪夫不等式，即使不知道具体的分布函数，只要知道准确的方差，我们就可以对期望进行初步的假设检验。

例如，已知一个分布的方差为1，问一次抽样取值在什么范围的时候能在0.05的显著性水平下拒绝总体期望为0的原假设。

解：写出原价设和备择假设，H0∶μ=0；H1∶μ≠0。

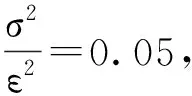
六、精确的假设检验——已知分布函数形式之后

契比雪夫不等式实际上给出了一个最宽泛的情况，就是不管什么分布肯定都存在这样的方差和期望之间的关系。实际上是给出了偏离期望的概率值的一个上确界。

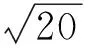
在知道总体分布的时候，我们可以获得更加精确的概率值去进行假设检验，就可以做更加严格的假设检验，可以在更不极端的情况拒绝原假设。如果我们已知总体的方差为1，并且知道总体是一个正态分布，我们就可以通过标准的正态分布表来获得检验期望为0对应的临界值。如果总体是某个自由度条件下的t分布，我们可以查相应的t分布表。如果总体是某些自由度参量下的F分布，我们也有表可查。

如果我们所要讨论的问题没有现成的概率表可以查，我们可以通过概率统计知识进行变换成合适的形式，然后进行查表操作。

这个情况下我们不仅能做精确的双边检验还能做精确的单边检验。

例，已知一个方差为9的正态分布，问取值在什么范围的时候能在0.05的显著性水平下拒绝如下问题中的原假设。

a)H0∶μ=0 H1∶μ≠2

b)H0∶μ≤2 H1∶μ>2

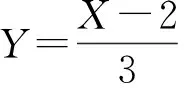
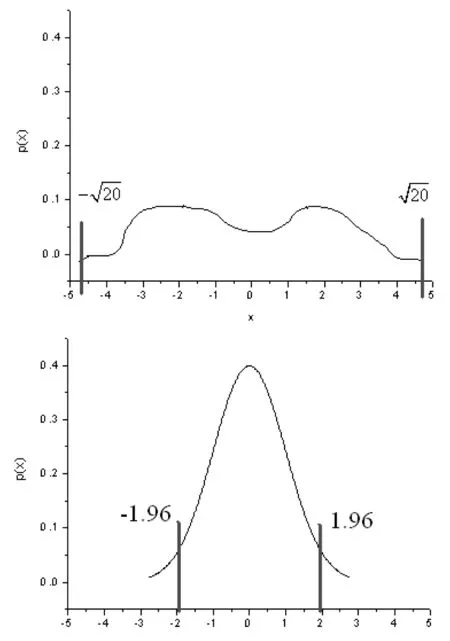
图1 在0.05显著性水平下拒绝期望为0的临界值

(上为任意分布情况，下为标准正态分布情况)

七、假设检验的抽样——根据一个逻辑抽样进行的

在计量经济学问题中，我们的样本往往有很多，这容易迷惑大家，造成一个误解，就是以为假设检验是多次来进行的。实际上并不是这样，这些数据将被计算成一个值，然后进行假设检验环节，也就是所有的假设检验最终本质上只是通过一次逻辑抽样进行的。

例如，我们已经在不知道分布形式也不知道方差的情况下，我们不能做假设检验。但如果我们多次抽样，我们就可以得到样本方差来近似代替总体方差得到进行近似的假设检验。即：

(3)

(4)

(5)

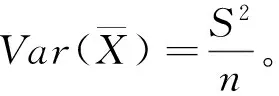
所以计量经济学中所广泛使用的单参数t检验的原因是因为总体误差项的方差未知，误差项方差已知的情况下是可以使用标准正态分布检验的，而不知道的时候我们用平均自由度下的残差平方和替代，从而使用的是t检验。

t检验中，我们只是构造出符合t分布的统计量，然后通过样本值计算了这个统计量的值，相当于做了一次这个统计量的抽样，然后根据统计量的特性进行假设检验。其他的F检验也是如此，是在原假设的基础上构造出来合适的统计量，然后通过样本数据计算了一个值。在原假设正确的情况下，这个值就是对服从某一个分布的统计量的一次抽样。

八、假设检验中的临界值比较——统计量的值、p值和置信区间

在计量经济学的假设检验中，经常有三种表现形式：(1)统计量的值，一般为单参数检验的t值和线性约束条件下的F值；(2)p值为统计量的值在相应的分布中对应的更远端的概率值；(3)置信区间是指一定置信度水平下某个值所处的区间，或者处于这个区间有一个相应的概率。

t值的计算已经考虑到需要检测的期望，所以得到t值后只能针对同样的原假设进行假设检验，但是可以在不同的显著性水平下做。具体做法是，根据不同的显著性水平从相应的统计分布表中查出相应的临界值。然后将得到的t值与临界值进行比较。

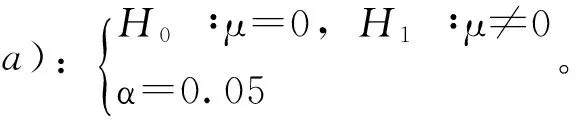
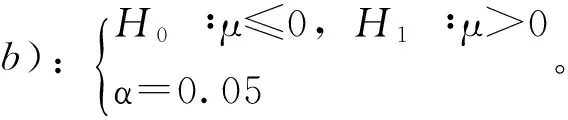
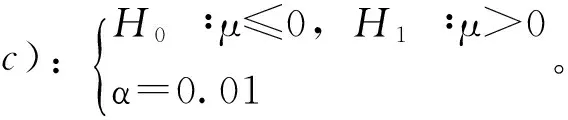
但如果通过t查表得到p值，不需要针对每个显著性水平查表，而是直接判断是否要拒绝原假设。如自由度为20的情况下，得到t统计量的值为2.08，该点相应的p值略小于0.05。就可以在0.05的显著性水平下通过双边检验不拒绝原假设，更可以在0.1的显著性水平下通过双边检验不能拒绝原假设，或者在0.025的显著性水平下通过单边检验拒绝原假设。同样，获得F值后也可以通过查表得到对应的p值，然后检查是否可以在一定的显著性水平下拒绝原假设。

以上通过统计量的值或者对应的p值都可以在不同的显著性水平下进行假设检验，但原假设不能变。如果我们在一定的置信度水平下得到真实值的对应的置信区间，则可以非常方便地对更多可能的原假设进行假设检验。

显著性水平和置信度水平是对应的。显著性水平0.05，对应概率95%置信区间。显著性水平0.01，对应的置信区间的概率为99%。

九、假设检验的扩展应用——预测

计量经济学中，单参数显著性的t检验和预测部分(条件期望预测和个值预测)是分开的，但是可以发现很多形式上是一样的，确实如此。只是在做条件期望预测或者点预测的时候是往往直接计算置信度区间，而不是计算统计量的值和p值，虽然实际上也可以那么做。

例如在多元回归中，我们对于实际可能发生的Y0|X0的讨论是如下进行的。

首先在满足经典假设的条件下，Y0|X0是一个正态分布随机变量，其期望是E(Y0|X0,X,Y)，方差是σ2。

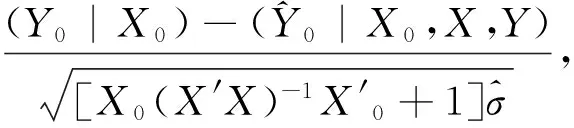
十、结论和讨论

我们上面总结的有关计量经济学中的假设检验逻辑框架只是一部分知识，里面谈到了很多自己的理解，很多内容可能并不是计量经济学所涉及的，但了解这些背景有助于对假设检验的全盘理解，有助于我们对于计量经济学的掌握和应用能力的提升，不管是从计量经济学的现代观点来看还是从更加经典的观点来看。

实际上，假设检验有更加深刻广泛的基础，它不仅限于计量经济学，社会统计学以及概率论和数理统计课程中都有大量内容与此相关。事实上，它更广泛存在于人类的社会的各个环节，我们认识事物的基本方式实际就是按下面的过程进行的。从这个角度来看，对于假设检验的理解具有更大的意义和价值。

〔1〕 李子奈，齐良书.关于计量经济学模型方法的思考[J].中国社会科学，2010(2)：69-83.

〔2〕 李子奈.关于计量经济学课程教学内容的创新与思考[J].中国大学教学，2010(1)：18-22.

〔3〕 王美今，林建浩.计量经济学应用研究的可信性革命[J].经济研究，2012(2)：120-132.

〔4〕 李晓宁,石红溶,徐梅.本科计量经济学教学模式改革的探索与比较[J].高等财经教育研究,2012(2):11-15.

〔5〕 余妙志,蒋烨.案例教学在计量经济学课程教学中的应用[J].课程教育研究,2014(5):245-246.

〔6〕 姚寿福,刘泽仁,袁春梅.本科计量经济学课程教学改革探讨[J].高等教育研究,2010(2):45-48.

〔7〕 李子奈，潘文卿.计量经济学[M].北京：高等教育出版社,2010.

〔8〕 杰弗里·M·伍德里奇.计量经济学导论——现代观点[M].北京：清华大学出版社,2014.

〔9〕 卡尔·波普尔.科学发现的逻辑[M].查汝强，邱仁宗，译.北京:中国美术学院出版社,2008.

〔10〕 李醒民.激动人心的年代:世纪之交物理学革命的历史考察和哲学探讨[M].北京：中国人民大学出版社,2009.

(责任编辑 周吉光)

How to Understand the Hypothesis Test in Econometrics

CHEN Qing-hua1, GUO Jin-zhong2, YUAN Qiang1

(1. Beijing Normal University, Beijing, 100875; 2. Xinjiang University, Urumqi, Xinjiang, 830047)

Hypothesis testing is the most important content in Econometrics and Mathematical statistics. But in relevant textbooks and teaching process, the authors and teachers often focus on the parameter estimation method, and the part of hypothesis testing is not deep enough, relevant knowledge background and logic process are not clear. Since that, the students do not really understand hypothesis testing, the last obstacle to the entire learning and application of econometrics. This article links to other background materials related to hypothesis testing refresh logic system, broaden their knowledge, analysis, hypothesis testing demonstrate knowledge related to various logical and contacts aimed at promoting students were econometrics hypothesis testing ideas really understand, promote real education reform in econometrics.

Econometrics; hypothesis testing; teaching reform

10.13937/j.cnki.sjzjjxyxb.2016.06.002

2016-05-23

http://www.cnki.net/kcms/doi/10.13937/j.cnki.sjzjjxyxb.2016.06.002.html < class="emphasis_bold">网络出版时间

时间：2016-12-20 15：30

北京师范大学教学建设与改革项目 (11-06-01-10)；新疆大学博士毕业生科研启动基金项目“新疆企业规模分布及其变化规律”(BS150110)。

陈清华(1976—)，男，湖北当阳人，博士，副教授，研究方向为复杂性理论及其在社会经济系统上的应用。

G642.0

A

1007-6875(2016)06-0007-06