高速列车传动系统特征参数经典域优化

刘玉梅， 赵聪聪， 熊明烨， 张志远，3， 乔宁国

（1．吉林大学交通学院，吉林长春130022；2．伊利诺伊大学厄巴纳-香槟分校自由艺术与科学学院，伊利诺伊厄巴纳-香槟61801；3．长春一汽解放汽车有限公司，吉林长春130000）

高速列车传动系统特征参数经典域优化

刘玉梅1， 赵聪聪1， 熊明烨2， 张志远1，3， 乔宁国1

（1．吉林大学交通学院，吉林长春130022；2．伊利诺伊大学厄巴纳-香槟分校自由艺术与科学学院，伊利诺伊厄巴纳-香槟61801；3．长春一汽解放汽车有限公司，吉林长春130000）

为监测高速列车传动系统的运行状态，根据可拓学理论，建立了传动系统各部件的运行状态物元，提出了一种部件正常运行状态下的特征参数经典域优化方法．利用部件样本集与其正常运行状态之间的最大综合关联度构建了适应度函数，并利用并行粒子群优化算法进行解算，确定了特征参数的经典域范围．与用数理统计方法得到的经典域结果进行了对比分析，结果表明，用本文经典域优化结果得到的最大综合关联度的最大值和平均值分别提高了3．63%和2．51%，经典域优化结果更符合部件的实际运行状况．

传动系统；可拓学；经典域优化；并行粒子群优化算法；统计方法

传动系统作为高速列车重要的组成部分，承担列车走行的重要功能，是影响列车行驶安全的关键系统之一［1-2］．随着列车运行速度提高和轴重增大，传动系统承载状况恶化，运行过程中将产生更大的安全隐患，实时监测传动系统各部件的运行状态对列车行车安全具有重要意义．可拓学作为新兴交叉学科，从定性和定量角度分析和解决问题，目前已应用于人工智能、计算机科学与技术、故障诊断、状态监测等领域［3］．

经典域是典型的可拓集合，精确给定经典域是应用可拓学理论进行故障诊断和状态监测的前提条件．经典域通常依据数理统计方法［4］或专家经验给出，具有一定的主观性和随意性，会直接影响判断结果的准确性．目前对于经典域的研究文献较少，文献［5］利用人工免疫网络算法，寻找起重机在不同起吊重物情况下操作仰角和旋转角的经典域，文献［6］引入Bootstrap算法确定经典域．

为确定传动系统结构部件在正常运行状态下物元特征参数的经典域，根据动力转向架传动系统的结构，建立传动系统关键部件的运行状态物元，得到特征参数的经典域矩阵；在综合关联函数的基础上，将部件运行状态样本集与其正常运行状态之间的最大综合关联度作为适应度函数，采用并行粒子群优化算法进行寻优求解，最终确定各部件正常运行状态下的特征参数经典域，并利用数理统计方法对比说明了本文经典域优化结果的正确性．以小齿轮轴承1为例，说明了可拓方法在传动系统部件状态监测中的应用，验证结果表明了本文经典域优化结果的有效性和准确性．

1 传动系统部件运行状态物元

1．1 可拓学相关概念

物元是可拓学的逻辑细胞，用有序三元数组R＝（N，C，V）［7-8］表示，其中N是事物，C是事物的特征，V是事物关于C的量值．设事物N共有m类状态，每类状态用n个特征参数表示，则处于状态j的事物Nj的经典域物元为

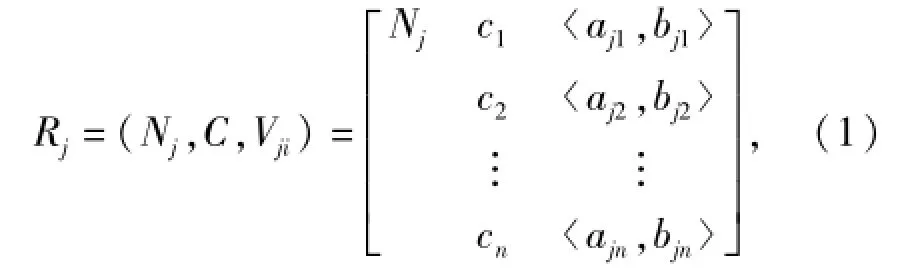
式中：C为事物的特征集，

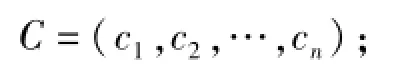
Vji为第j类状态第i个特征参数的经典域，

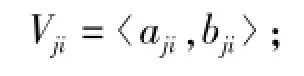
aji、bji为Vji的下限和上限，j＝1，2，…，m，i＝1，2，…，n．

节域是所有经典域的集合，节域物元表示为

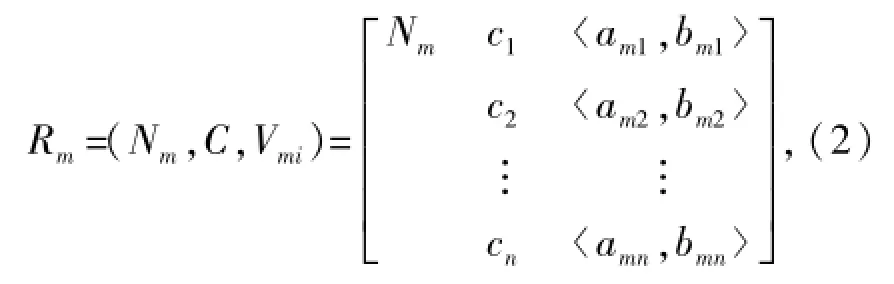
式中：Nm为事物所有分类状态；

Vmi为所有分类状态下第i个特征参数的节域；ami、bmi为Vmi的下限和上限，i＝1，2，…，n．

1．2 部件运行状态物元

图1所示为某架悬式转向架传动系统结构．其中动力转向架包括两套传动系统，牵引电机直接或通过悬吊装置固装在转向架构架上；齿轮箱通过悬吊装置与转向架构架相连；从动大齿轮压装在车轴上，牵引电机与齿轮箱之间通过联轴器传递扭矩．

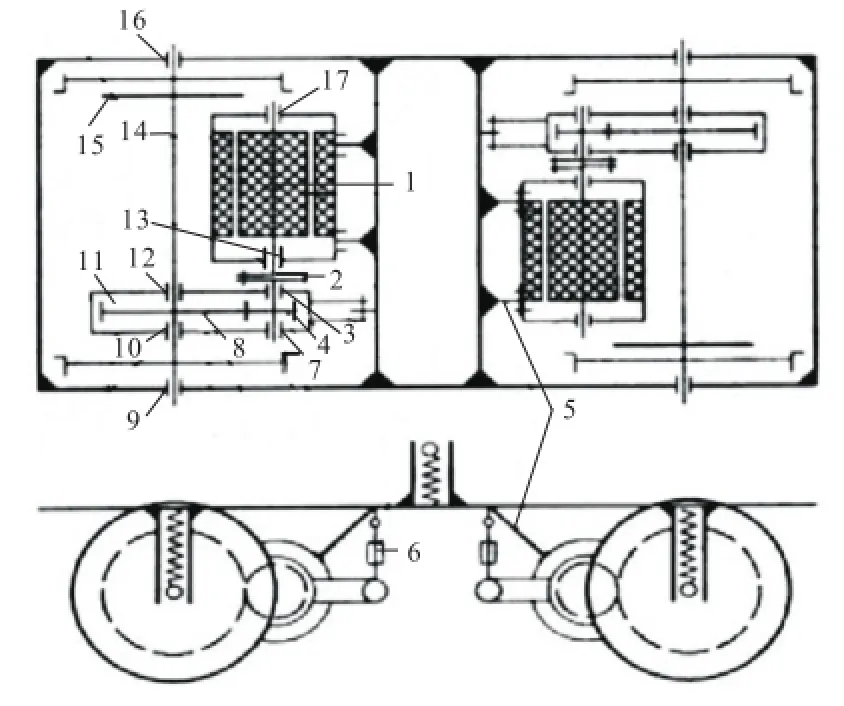
图1 架悬式转向架传动系统结构Fig．1 Structure of the bogie-mounted transmission system

由列车实际线路运行故障统计及仿真试验模拟结果发现，牵引电机输出轴轴承、齿轮箱轴承、联轴器、传动轴等部件在未满服役期内经常发生较严重的损坏［9］．本文对电机轴承1、小齿轮轴承1和2、大齿轮轴承1和2、轴箱轴承1和2、联轴器、齿轮箱箱体、传动轴共10个传动系统组成的部件进行分析，确定各部件正常运行状态物元的特征参数经典域．建立传动系统部件的运行状态物元：

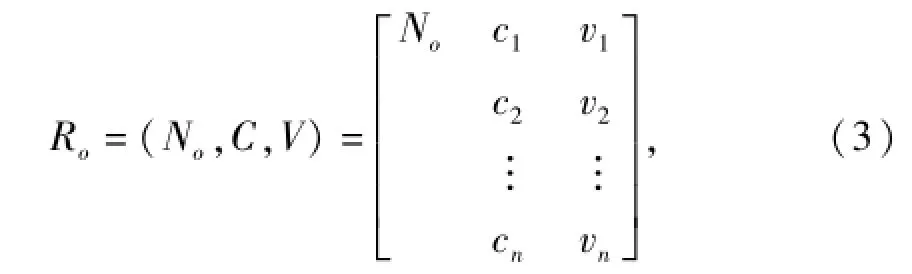
式中：No（o＝1，2，…，10）为传动系统第o个部件的运行状态，包括正常状态及所有异常状态；

ci（i＝1，2，…，n）为部件运行状态的特征参数；

vi为特征参数ci的量值．

根据式（1）和（3），得到传动系统各部件在正常运行状态下的特征参数经典域矩阵

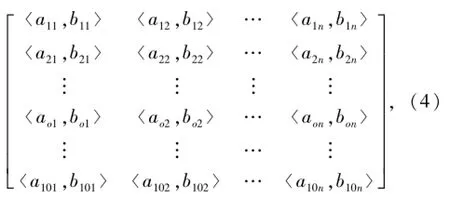
式中：Voi＝〈aoi，boi〉为部件o正常运行状态下第i个特征参数的经典域，aoi、boi为Voi的下限和上限，o＝1，2，…，10，i＝1，2，…n．

2 经典域优化方法

2．1 经典域优化数学模型

用部件当前状态与正常状态之间的综合关联度反映部件的当前运行状态．利用综合关联函数为基础，构建部件正常运行状态下的特征参数经典域优化模型．综合关联函数以初等关联函数为基础，设X0＝〈x1，x2〉，X＝〈x3，x4〉，X0⊂X，且X0与X无公共端点，则初等关联函数［10-11］表示为

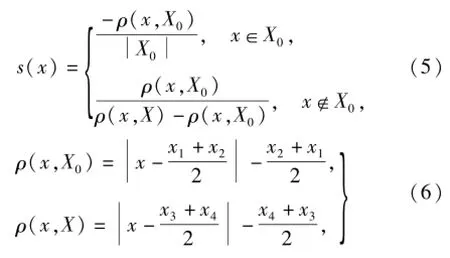
式中：X0和X分别为经典域和节域；s（x）为元素x关于区间X0的关联度，其正负及大小表明x属于或不属于X0的程度．

设式（3）中特征参数权重集为W＝｛w1，w2，…，wn｝，则各部件与其正常运行状态之间的综合关联度为

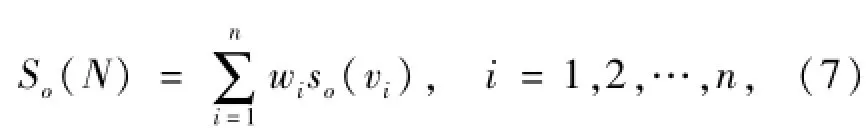
式中：So（vi）为部件当前运行状态物元第i个特征参数值vi与其正常运行状态物元第i个特征参数经典域Vji之间的关联度．

若已知各部件正常运行状态下的特征参数样本集，则由综合关联度的意义可知，样本集与正常状态之间的综合关联度非负，且综合关联度越大，表明已知样本集与正常运行状态之间的相关程度越大．因此，利用可拓学的综合关联函数，将特征参数的经典域优化问题转化为对关联函数进行最大值求解的数学问题，其数学表达如下：

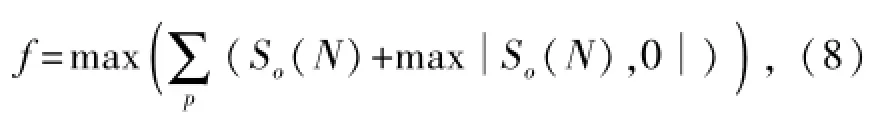
式中：p为样本组数．

2．2 并行粒子群优化算法

并行粒子群优化算法作为一种改进的PSO（particle swarm optimization）算法，将粒子群划分为多个子群，各子群相互独立地执行PSO算法，能够有效解决PSO算法计算精度低、易陷入局部极小和早熟收敛等问题［12-13］．并行粒子群优化算法流程如图2所示．

由于粒子速度代表每次迭代过程中，粒子靠近或远离当前位置的大小，第l个子群粒子的速度和位置更新公式［14］如下：

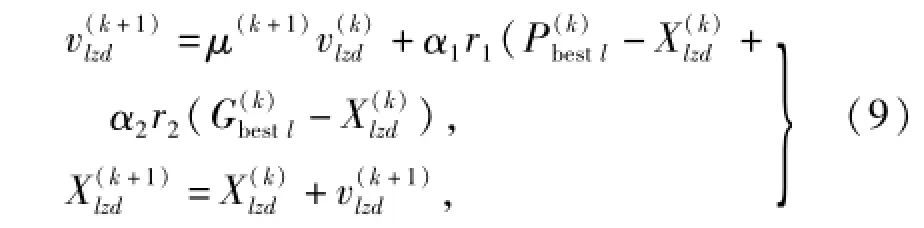
α1、α2为加速因子，取值在1～2之间；

r1、r2为［0，1］区间的随机数；

μ为粒子速度更新惯性权重，

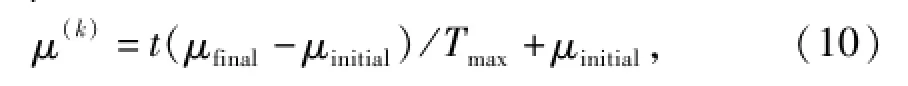
式中：μinitial为初始权重；

μfinal为最终权重；

t为当前迭代次数；

Tmax为最大迭代次数．

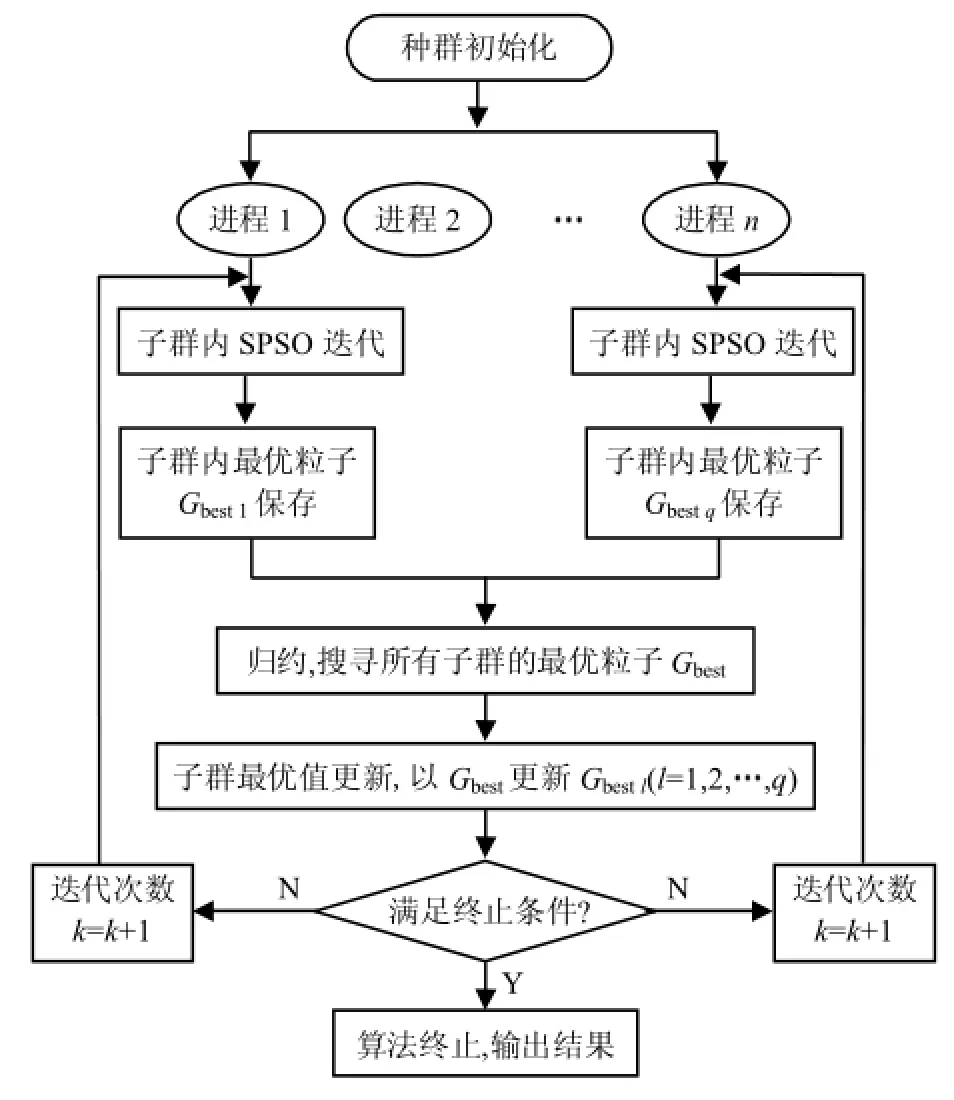
图2 并行粒子群优化算法流程Fig．2 Flowchart of parallel PSO algorithm

3 传动系特征参数经典域优化

3．1 部件运行状态特征参数

由于小波变换在时域和频域具有较强的信号局部特征表征能力，并且小波能量能够反应信号在小波变换各频带内的能量分布信息［15］，因此，本文以振动加速度信号在各频带的小波能量作为部件运行状态物元的特征参数．式（3）中，ci（i＝1，2，…，n）表示部件振动加速度信号在各频带的小波能量，vi为相应的小波能量值．

利用振动加速度传感器，获得传动系统各组成部件在正常运行状态下的振动加速度信号，构建特征参数样本集．数据采集系统的采样频率为2 048 Hz．从各部件的振动信号中选取25组数据，每组包含4 096个数据点，用db3小波进行4层小波分解．将得到的小波能量以每5组为1个单位进行均值处理，得到各部件在正常运行状态下的5组小波能量数据，以此作为确定部件正常运行状态特征参数经典域的样本集，部分样本集见表1．

3．2 特征参数经典域优化

在对适应度函数式（8）进行优化之前，首先需要确定粒子各维的可行解空间，即粒子可能达到的范围空间．本文中粒子的可行解空间对应于特征参数的节域．以小波能量作为特征参数，根据小波能量的性质可知其取值区间为［0，100］，即粒子各维运动空间为0～100．

本文中设种群粒子数为20，子群个数q＝4，按式（10）更新惯性权重，

加速因子

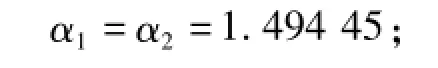
终止阈值

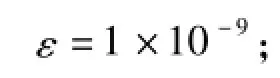
粒子维数

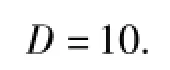
为降低粒子离开搜索空间的几率，限定粒子最大速度为空间范围的20%．为保证迭代过程中aoi＜boi，对粒子位置进行限定：

式中：a′oi、b′oi为迭代过程中的粒子位置．

设部件运行状态物元中各特征参数的权系数按等权处理，即wi＝1／5．以表1为样本集，采用并行粒子群优化算法对式（8）进行寻优解算，得到各部件正常运行状态下各频带小波能量参数的经典域，结果见表2．图3为利用本文方法确定电机轴承1特征参数经典域的最佳适应度值变化曲线．

表1 各频带的小波能量样本集Tab．1 Sample sets of wavelet energy in each frequency band

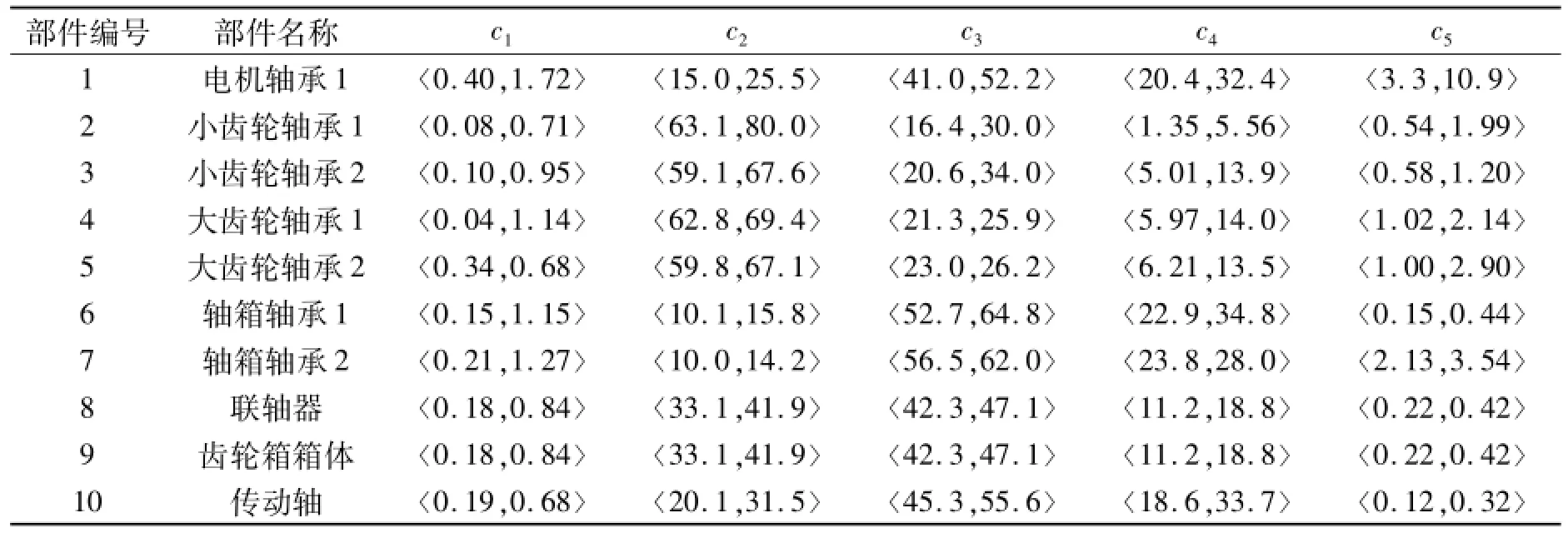
表2 各部件正常运行状态下的特征参数经典域Tab．2 Classical domains of characteristic parameters for components in normal running state

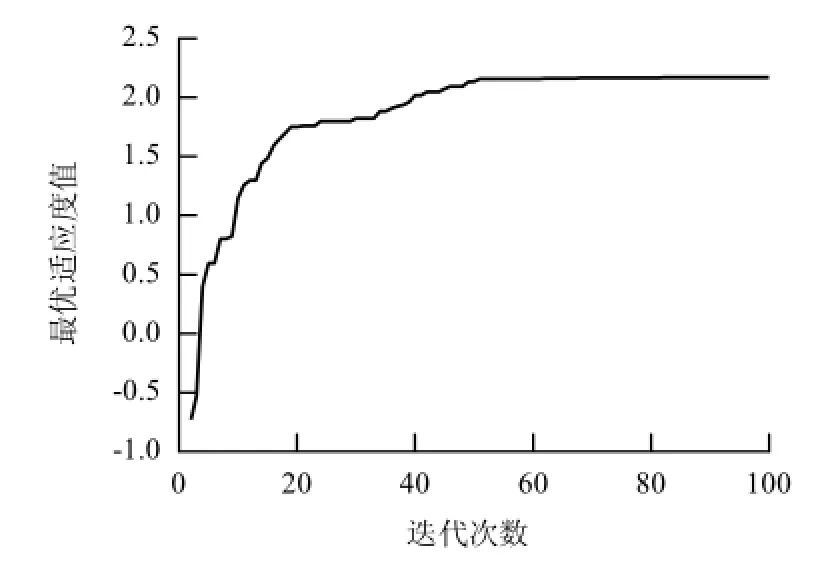
图3 电机轴承1的最佳适应度值变化曲线Fig．3 Trend curve of the best fitness value for motor bearing 1

3．3 结果验证

以基于数理统计确定的经典域作为对比，对本文经典域优化结果的有效性进行说明．设随机变量X的均值和方差分别为XE和σ2，根据切比雪夫不等式

令ε＝4σ，B则随机变量X落在4个标准差范围内的概率为93．75%．为降低小样本数据引起的计算误差，利用前文所述方法获得50组样本集，根据式（12）得到各部件正常运行状态下的特征参数经典域，结果见表3．

由综合关联度定义知，若从传动系统部件正常运行状态数据中抽取样本，对样本数据进行特征提取并构建部件运行状态物元，则部件当前运行状态与其正常运行状态之间的综合关联度越大表明二者之间的相关程度越强．从传动系统各部件的运行状态数据中提取3组特征参数，分别用上述两种经典域结果计算综合关联度，结果如图4所示．

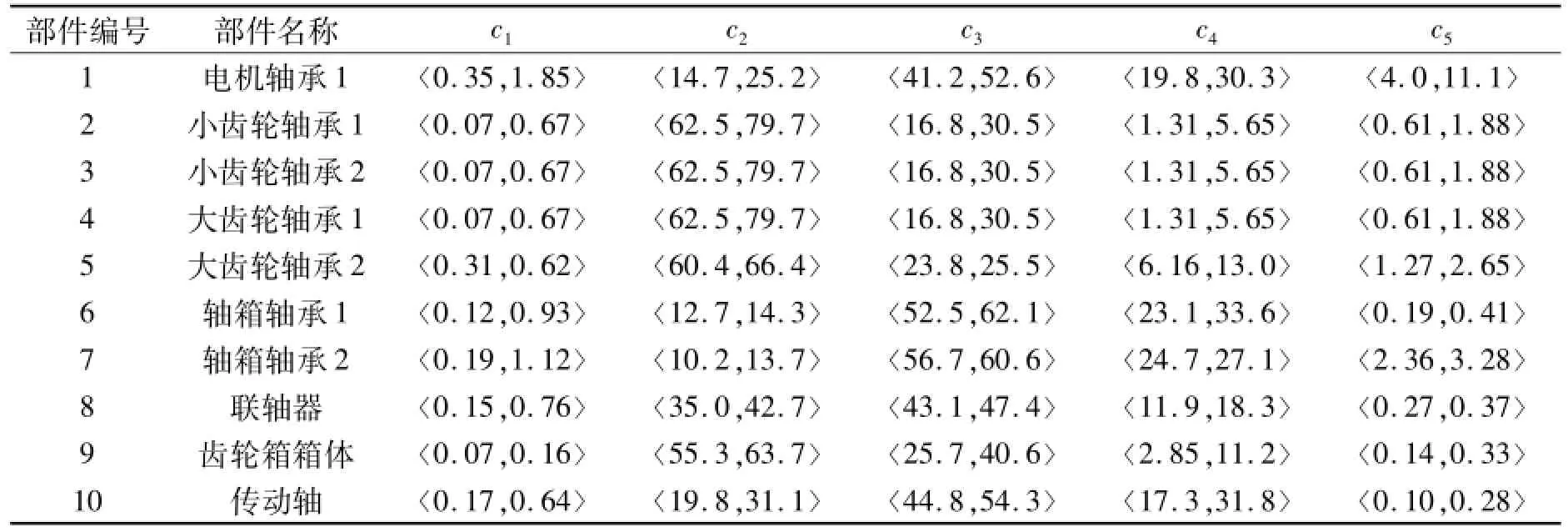
表3 数理统计方法确定的经典域Tab．3 Classical domains determined by statistic method

图4横坐标表示传动系统的结构部件，编号与表2对应，纵坐标为部件与其正常状态之间的综合关联度．

由图4知，与统计方法经典域结果相比，利用本文方法优化经典域结果得到的最大综合关联度最大值提高了3．63%，平均提高了2．51%，说明优化方法确定的经典域不仅符合概率分布的一般规律，而且能更准确地表征部件的实际状态．

为进一步验证经典域优化结果的正确性，并说明可拓学方法在轨道车辆传动系统部件运行状态监测中的应用，以小齿轮轴承1为例，绘制小齿轮轴承1当前状态与其正常状态之间的综合关联度-时间曲线，如图5所示．

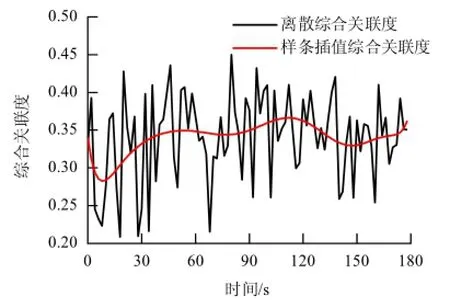
图5 小齿轮轴承1的综合关联度-时间曲线Fig．5 Comprehensive degree-time curve for pinion bearing1

图5 中综合关联度为正，说明小齿轮轴承1正常运行，与已知状态一致；综合关联度的样条插值曲线较为平缓，说明小齿轮轴承1以健康状态持续运行．

4 结 论

针对高速列车传动系统特征参数经典域的确定问题，在综合关联函数基础上提出了一种适应度函数，利用并行粒子群优化算法进行寻优求解，确定了各部件在正常运行状态下的特征参数经典域．采用数理统计方法对经典域优化结果的有效性进行了对比说明，并以小齿轮轴承1为例，说明了可拓方法在传动系统部件运行状态监测中的应用．结果表明，与统计方法相比，利用优化经典域结果得到的最大综合关联度最大值提高了3．63%，平均值提高了2．51%，说明了本文经典域优化结果的正确性和可靠性．

致谢：长春市科技支撑计划项目（2010018）．

［1］ 李熙．城市轨道交通车辆走行部安全评估方法研究［D］．北京：北京交通大学，2011．

［2］ LEE C W，LEE D H．Design life analysis of KTX running gear systems on various operating conditions［J］．Key Engineering Materials，2015，625：674-677．

［3］ CHAO K H．The application of extension algorithms in induction motor mechanical fault diagnosis［J］．Key Engineering Materials，2010，426／427：593-598．

［4］ 李明，李广杰，张文．基于概率统计的可拓学分析方法在边坡岩体质量分级中的应用［J］．吉林大学学报：地球科学版，2011，41（5）：1488-1493，1503．LI Ming，LI Guangjie，ZHANG Wen．Slope rock mass quality classification based on extenics analysis of probability statistics［J］．Journal of Jilin University：Earth Science Edition，2011，41（5）：1488-1493，1503．

［5］ 向长城．基于免疫网络算法关联函数经典域优化［J］．湖北民族学院学报：自然科学版，2009，27（4）：370-375．XIANG Changcheng．Classical fields optimum of independent function based on artificial immune network algorithm［J］．Journal of Hubei University for Nationalities：Natural Science Edition，2009，27（4）：370-375．

［6］ 张金春，张家宾，李超亚，等．可拓模式识别算法中经典域的确定方法［J］．海军航空工程学院学报，2015，30（1）：87-90．ZHANG Jinchun，ZHANG Jiabin，LI Chaoya，et al．The method of determining classical domain with the extension pattern recognition algorithm［J］．Journal of Naval Aeronautical and Astronautical University，2015，30（1）：87-90．

［7］ QIU Gefei，XIE Zhaoxiang，HUANG Sheng，et al．Transformer fault diagnosing method based on extenics and rough set theory［J］．International Journal of Security and Its Applications，2014，8（5）：65-74．

［8］ LIU JF，OU G Q，YOU Y．Slope stability assessment based on fuzzy matter-element extension model［J］．Applied Mechanics and Materials，2012，170／171／172／173：366-370．

［9］ 郭文翠．基于可拓论的高速轨道车辆传动系统疲劳损伤分析［D］．长春：吉林大学，2013．［10］ LI Hongze，GUO Sen．External economies evaluation of wind power engineering project based on analytic hierarchy process and matter-element extension model［J］．Mathematical Problems in Engineering，2013，Article ID 848901．

［11］ HE Yongxiu，DAI Aiying，ZHU Jiang，et al．Risk assessment of urban network planning in china based on the matter-element model and extension analysis［J］．International Journal of Electrical Power and Energy Systems，2011：33（3）：775-782．

［12］ HU H．Parallel PSO-based optimal strategy study of energy efficient operation control for train［J］．Advanced Materials Research，2012，605-607：1861-1865．

［13］ SHAO Bo，LIU Jiansheng，HUANG Zhigang，et al．A parallel particle swarm optimization algorithm for reference stations distribution［J］．Journal of Software，2011，6（7）：1281-1288．

［14］ FENG Lei，WEI Wei．Research of PSO／genetic algorithms and development of its hybrid algorithm［J］．International Journal of Digital Content Technology and its Applications，2012，6（11）：328-335．

［15］ 张进，冯志鹏，褚福磊．滚动轴承故障特征的时间：小波能量谱提取方法［J］．机械工程学报，2011，47（17）：44-49．ZHANG Jin，FENG Zhipeng，ZHU Fulei．Extraction of rolling bearing fault feature based on time-wavelet energy spectrum［J］．Journal of Mechanical Engineering，2011，47（17）：44-49．

（中文编辑：秦萍玲 英文编辑：兰俊思）

Optimization of Classical Domains for High-Speed Train Transmission System

LIU Yumei1， ZHAO Congcong1， XIONG Mingye2， ZHANG Zhiyuan1，3， QIAO Ningguo1
（1．College of Traffic，Jilin University，Changchun 130022，China；2．College of Liberal art and science，University of Illinois at Urbana-Champaign，Champaign-Urbana 61801，USA；3．FAW Jiefang Automotive Company Ltd．，Changchun 130000，China．）

In order to monitor the operating condition ofa high-speed train transmission system，matter elements that present the operating condition of components of the transmission system were established by the extension theory，and an optimization method for determining the classical domains of characteristic parameters of the matter element that presents a component's normal operating condition was proposed．In this method，a fitness function was constructed using the maximum comprehensive correlative degree（MCCD）between a component's sample sets and its normal operating condition．Then，the parallel particle swarm optimization（PSO）algorithm was adopted to solve the fitness function and determine the classical domains．In addition，the optimization results of classical domains were compared with those determined by the statistical method．The results show that the maximum and average of MCCDs obtained from the optimization results of classical domains are improved by 3．63% and 2．51%，respectively，which demonstrates that the optimization results of classical domains more conform to components'actual operating conditions．

transmission system；extension；optimization of classical domains；parallel PSO；statistical method

U262．3

A

0258-2724（2016）01-0085-07

10．3969／j．issn．0258-2724．2016．01．013

2015-04-10

国家自然科学基金资助项目（51575232）；“十一五”国家科技支撑计划项目（2006BAG01B03）；吉林省科技厅自然基金项目（201215020）

刘玉梅（1966—），女，教授，研究方向为车辆智能检测与故障诊断及虚拟仿真与测试等，E-mail：lymlls＠163．com

刘玉梅，赵聪聪，熊明烨，等．高速列车传动系统特征参数经典域优化［J］．西南交通大学学报，2016，51（1）：85-90，120．